带悬吊质量结构的多维地震反应

魏文晖，张 迪，喻 梦，吴其伟

带悬吊质量结构的多维地震反应

魏文晖，张 迪，喻 梦，吴其伟

（武汉理工大学道路桥梁与结构工程湖北省重点实验室，430070武汉）

为了研究带悬吊质量结构体系在地震动水平-竖向-摇摆耦合作用下的动力效应，推导了地震动水平-竖向-摇摆耦合作用下带悬吊质量结构体系的动力方程，提出一种改进的摇摆分量时程获取方法，并以某带悬吊质量阀厅结构为原型，进行1∶10缩尺模型振动台试验，探讨采用不同长度的钢索和弹簧悬吊质量时，结构在水平-竖向、摇摆-竖向和水平-竖向-摇摆耦合地震动作用下的地震效应.结果表明：相较于水平地震动作用下，悬吊质量对摇摆地震动作用下主体结构的减震效果更加显著；随着钢索或弹簧长度增加，悬吊质量对主体结构的减震效果降低；将拉索由钢索改为同等长度的弹簧后，结构顶层的加速度响应和位移响应变化不大，但拉索动拉力却明显减小，当采用悬吊质量作为质量摆减震系统时，拉索应尽量采用弹簧或拉压刚度较低的构件.

地震反应；悬吊体系；地震动；摇摆波；振动台试验

带悬吊质量结构体系是土木工程中一种常用的结构形式［1］，该类结构在计算地震响应时，为了简化计算，通常仅考虑水平地震动和竖向地震动作用，而忽略摇摆地震动对该类结构的影响.实际上，震源附近（近震）的摇摆地震动产生的动力效应是非常显著的，许多结构的破坏和倒塌都与摇摆地震动有关［2-4］，例如1971年San-Fernando地震中，水平和摇摆耦合地震作用导致了桥梁的垮塌［5］.特别是对于带悬吊质量结构体系，摇摆地震动会使悬吊质量产生较大的摆幅和偏转角，导致其对主体结构的动力效应更加显著.由于几乎没有摇摆地震动时程的实测记录［6-9］，因此，对于摇摆分量时程的获取是一个急需解决的问题. Vladimir Graizer等［3］在2006年提出了基于单摆式地震仪记录的水平分量中通常掺杂着摇摆分量的原理，通过滤波获取摇摆分量时程的方法，并在振动台试验和震后实地观测中得到验证，为工程结构在摇摆地震动作用下的地震效应分析打下了基础.但该方法在实际运用中会存在特征频率不易确定等缺陷.另外，国内外学者虽已对摇摆地震动作用下工程结构的动力效应进行了大量研究［10-14］，这些研究均为常规结构体系，缺乏对带悬吊质量结构体系的研究.本文对文献［3］的方法进行改进，获取摇摆地震动时程，对地震动水平-竖向-摇摆耦合作用下带悬吊质量结构体系的动力效应进行理论分析，推导了考虑悬吊质量转动惯量影响的动力方程.并以一换流站阀厅（一种典型的带悬吊质量结构）为研究对象，进行1∶10缩尺模型振动台试验，探讨带悬吊质量结构体系在地震动水平-竖向，摇摆-竖向，以及水平-竖向-摇摆耦合作用下的动力效应，从而为此类结构体系的抗震设计计算和结构控制分析提供依据.

1 地震动水平-竖向-摇摆分量作用下带悬吊质量结构动力方程

带悬吊质量结构体系在地震动水平-竖向-摇摆耦合作用下，由于摇摆地震动的影响，悬吊质量自身的转动惯量成为一个不可忽略的因素，在动力方程推导过程中应予以考虑.而由于支柱的竖向刚度较大，可忽略顶层横梁转动惯量的影响.图1为带悬吊质量结构体系在地震动水平-竖向-摇摆耦合作用下的原结构及位移变形图，图2为横梁和悬吊质量的受力图.

图1中，支柱和横梁质量集中到m1，拉索和悬吊质量集中到m2；单层框架的层间侧向刚度为kcu，支柱竖向刚度为kcv，拉索的总竖向刚度为ks；悬吊质量对其形心的转动惯量为Jc；悬吊质量形心C到其顶面的距离为h，到两端的距离为a，拉索长度为L，支柱高为H．其他位移和角度参数意义见图中所示，并假设变形均为小变形．

图1 结构体系原结构及位移变形图

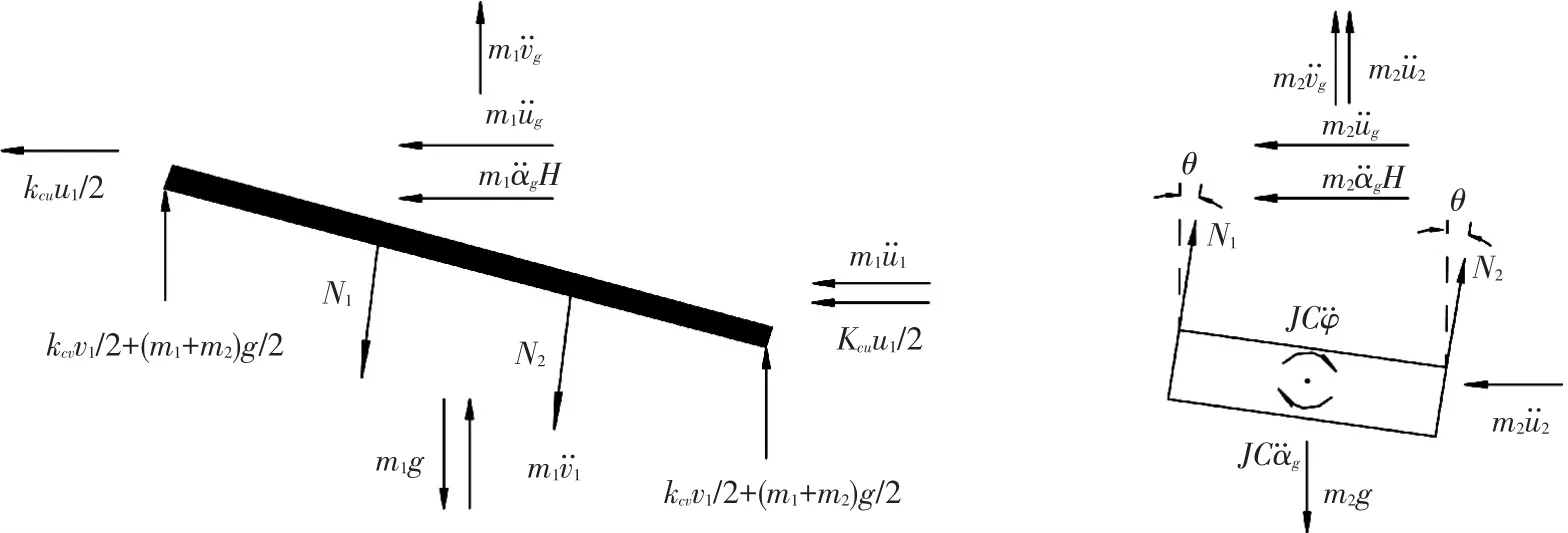
图2 横梁和悬吊质量受力图

由图1可知，左、右拉索的伸长分别为v2-v1+aφ和v2-v1-aφ，拉索的内力分别为

将式（1）代入式（2），其中，v1不包括由m1和m2产生的静位移，k1=m2g／L，k2=ksa2-m2gh，且θ=（u2-u1+hφ）／L，消去高阶微量，并写成矩阵形式，可得

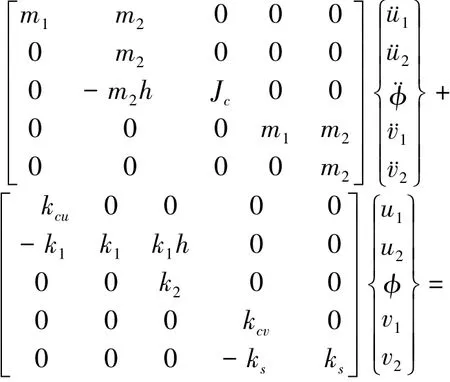
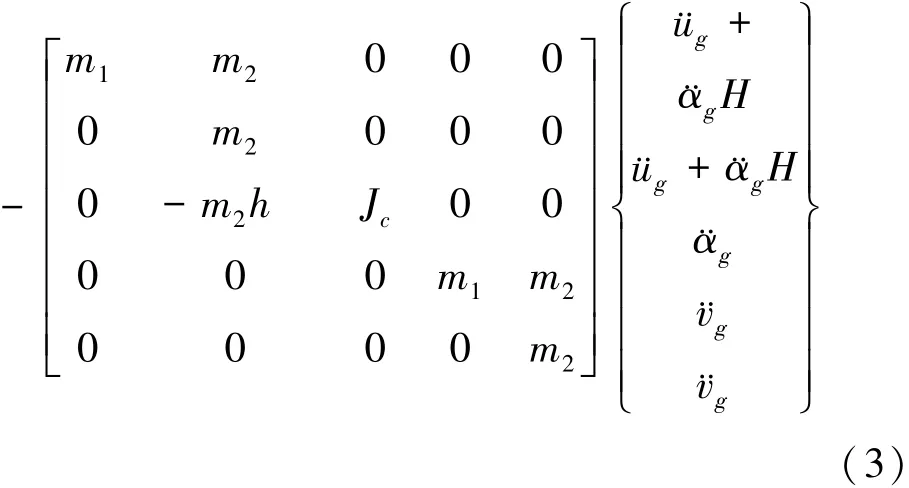
阻尼矩阵可采用瑞雷阻尼矩阵形式．由方程可以看出，随着主体结构高度H增大，¨αgH增大，摇摆地震动对结构的动力效应也将增大．另外，悬吊质量的转动惯量对摇摆地震动作用下结构的地震效应也存在较大的影响．

2 摇摆地震动时程的获取

本文是对文献［3］方法进行改进后得到的摇摆地震动时程.其方法主要步骤是先求出未修正的地震动水平与竖向分量加速度时程的傅里叶谱比值（修正后地震动时程常将摇摆分量作为噪声滤除）；根据其比值确定特征频率；最后以特征频率为界限，滤除水平分量中高于特征频率的部分，从而提取出掺杂在水平分量中的摇摆分量时程.

上述方法操作步骤虽然简单，但关键的特征频率，由于各种影响因素的存在，常常不易确定.水平与竖向傅里叶谱比值在残余倾斜存在的情况下，会在低频的范围内始终大于1，而文献［3］方法选取的特征频率是该比值大于2时的频率.但对多条震后存在倾斜的地震波时程进行处理时发现:若残余倾斜较小，该比值一般不大，不易确定相应的特征频率；若倾斜较大，比值大于2的频率范围也可能很小，所以采用此特征频率进行滤波得到的残余倾斜变形常常与实际记录不符.

本文对特征频率的确定方法进行改进，选取美国加州1994年Northridge地震Pacoima大坝左上侧站点的未修正地震波数据进行分析，获取其摇摆分量时程.地震波水平（210度分量）和竖向加速度时程如图3所示.

对上述未修正的地震波时程进行傅里叶变换得到其傅里叶谱，并求出水平加速度210度分量的傅里叶谱与竖向分量的比值，如图4所示.由图4可知:该比值在0～0.45 Hz时大于1，在0.6 Hz左右等于2，在1.55 Hz左右达到了13.8，之后有较大波动，在2 Hz左右又等于1，之后在1左右上下波动.因此分别选取特征频率为0.6、1.9 Hz，对水平地震动时程进行低通滤波.另外，由于未修正的地震动水平加速度时程时间间隔不全相同，在获取了地震动摇摆分量时程后，还应对其进行FFT平滑处理，进一步去除滤其中的高频成分，减小由于时间不等间隔而造成的偏差.最终获取的摇摆地震动时程如图5所示.

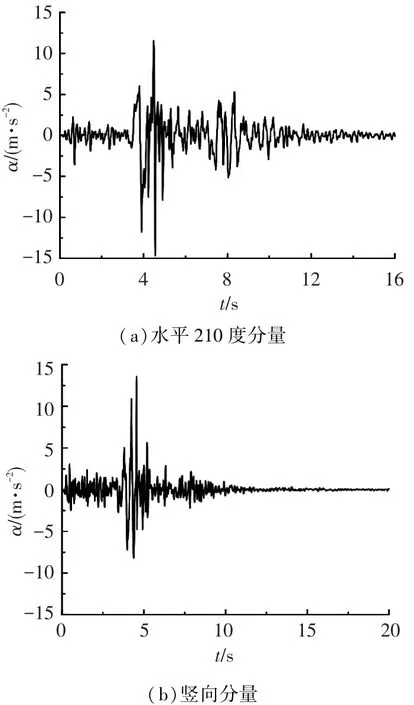
图3 Northridge地震Pacoima站点未修正地震波水平（210度分量）和竖向加速度记录

图4 水平加速度与竖向分量的傅里叶谱

图5 0.6 Hz和1.9 Hz滤波获取的摇摆地震动时程

对上述摇摆加速度时程进行两次积分，得到其倾斜位移时程如图6所示.并与CSMIP（加州强震观测计划）的员工在震后几天运用精确度为0.1°的电子水准仪测得的210度分量方向的残余倾斜位移（约为0.039 rad）进行对比，发现以1.9 Hz作为特征频率求得的残余倾斜函数与实际结果虽然有一定的误差，但比0.6 Hz的更为理想.因此，选用图5中以1.9 Hz作为特征频率获取的摇摆地震动时程.

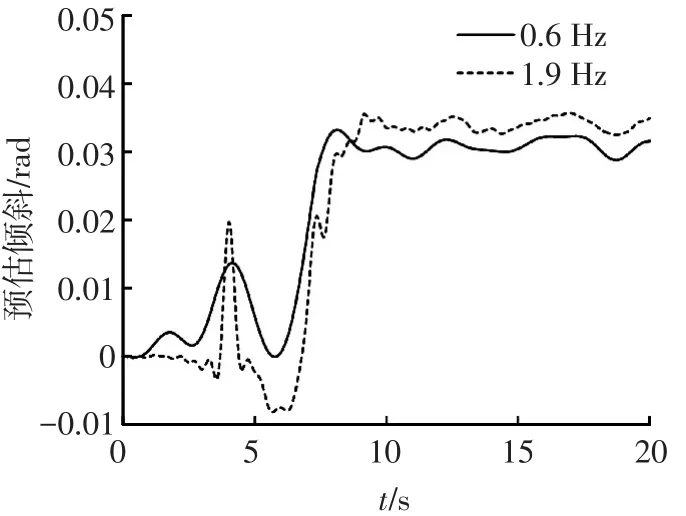
图6 0.6 Hz和1.9 Hz的倾斜位移时程

3 地震动水平-竖向-摇摆作用下带悬吊质量结构体系的振动台试验研究

本次试验在重庆交通科研设计院振动台试验室完成.试验目的是研究拉索为弹簧或钢索时的带悬吊质量结构体系，在地震动水平-竖向、摇摆-竖向和水平-竖向-摇摆耦合作用下主体结构的动力效应.

3.1 试验模型设计和拾振器布置

该试验模型以某换流站阀厅结构为原型，此阀厅为一单层钢框架结构，高度为21.6 m、跨度为18 m，屋架上悬吊大型阀塔，结构的基本自振周期约为0.48 s.试验模型缩尺比例为1∶10，模型结构设计图及实物照片如图7所示，立柱为56 mm×10 mm的钢管，主次梁为L50 mm×4 mm的角钢.顶层钢结构和人工质量共重100 kg，悬吊质量和配重盒共重100 kg.试验时，分别采用钢索和弹簧来悬吊质量，索长为0.2 m时，单根钢索和弹簧的拉压刚度分别为2.06×107N／m和6.13× 103N／m.由于本项试验重点是探讨地震动水平-竖向-摇摆耦合作用下带悬吊质量结构的主体结构动力效应，因此没有完全满足原结构的相似性，但试验模型的基本自振周期、几何尺寸、整体刚度满足相似原则.试验中的拾振器布置见图7，其中A1、A2和B1测点布置水平拾振器，A3和B2测点布置竖向拾振器，振动台两侧布置水平和竖向拾振器．钢索和弹簧连接部位C1位置贴应变片，测量钢索和弹簧的动应变．

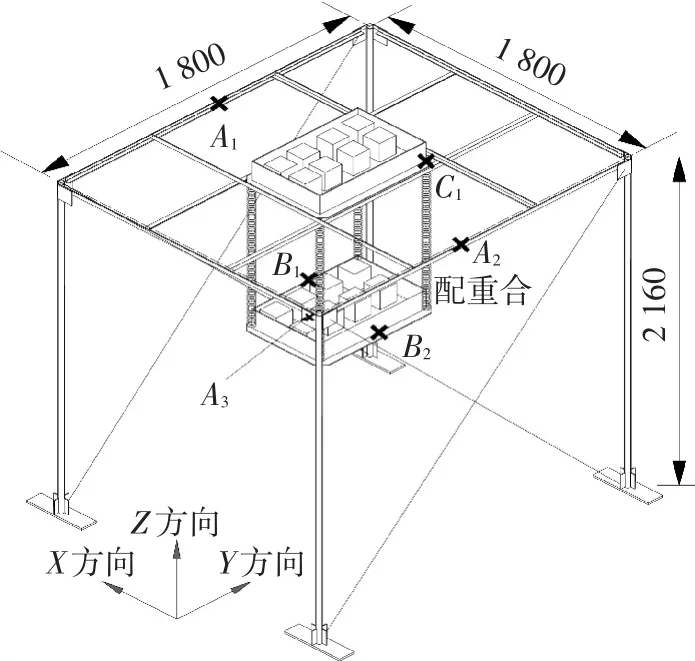
图7 试验模型结构设计图

3.2 试验工况

试验采用图3中所示的1994年Northridge地震的Pacoima大坝左上侧站点的地震波水平加速度210度分量和竖向加速度以及图5中所示的与1.9 Hz对应的摇摆分量时程.并将水平地震波时程峰值调整为6.2 m／s2（相当于9度罕遇地震），竖向和摇摆地震波时程乘以相同的比例系数，峰值分别为5.78 m／s2和0.246 rad／s2.试验中，水平（H）、竖向（V）和摇摆（T）地震波分别沿图7所示的X、Z方向输入和绕Y轴摆动，时间压缩0.316倍.试验模型结构形式分为纯框架和采用0.2、0.4、0.8 m的钢索或弹簧悬吊质量时的带悬吊质量框架.试验工况分为地震动水平-竖向、摇摆-竖向和水平-竖向-摇摆耦合作用.每次模型改变时，采用白噪声扫频，每个工况试验两次，试验结果取其平均值，水平白噪声峰值为0.5 m／s2.

3.3 试验结果

框架顶层水平加速度和位移.加速度时程由各拾振器直接测量得到，位移时程为加速度（速度）时程积分得到.各试验模型在各工况下的框架顶层水平加速度和位移幅值及影响系数见表1～4，表中amax、wmax分别为框架顶层水平加速度、位移幅值，影响系数μa（μw）表示带悬吊质量框架的amax（wmax）与纯框架的amax（wmax）之差与纯框架的amax（wmax）的比值，拉索为0 m时为纯框架；拉索为0.2 m弹簧时的框架顶层水平加速度时程a如图8所示、水平位移时程w如图9所示.由于篇幅限制，省略其他索长的顶层水平加速度和位移时程图.

由表1～4和图8、9可以看出:1）纯框架在地震动摇摆-竖向分量作用下的顶层水平加速度幅值约为水平-竖向分量作用下的54%，说明摇摆地震动产生的动力效应是不可忽略的；2）在摇摆-竖向分量作用下，索长变化对框架顶层水平加速度和位移幅值的影响都较大，当索长为0.2 m钢索时，加速度和位移的减震效果可分别达-14.5%和-19.2%，随索长的增加，减震效果均降低；在水平-竖向-摇摆耦合作用下，由于包含了摇摆地震动，索长变化对框架结构顶层水平加速度和位移幅值的影响仍较大，当索长为0.2 m钢索时，加速度和位移的减震效果为-11.2%和 -12.6%，随索长的增加，减震效果降低；3）索长变化使位移幅值减小的程度要大于使加速度幅值减小的程度；4）在同等条件下，拉索为钢索和弹簧时，框架顶层水平加速度和位移影响系数差别均不大.

表1 不同钢索长度时框架顶层水平加速度幅值及影响系数

表2 不同弹簧长度时框架顶层水平加速度幅值及影响系数

表3 不同钢索长度时框架顶层水平位移幅值及影响系数

表4 不同弹簧长度时框架顶层水平位移幅值及影响系数

图8 0.2 m的弹簧时的框架顶层加速度时程

图9 0.2 m的弹簧时的框架顶层位移时程

表5 不同钢索长度时拉索动拉力幅值及影响系数

表6 不同弹簧长度时拉索动拉力幅值及影响系数

拉索动拉力.拉索动拉力是指悬吊质量在摆动时对拉索产生的动拉力，不包括悬吊质量自重产生的静拉力.动拉力是根据拉索连接部位（图7中C1位置）的动应变幅值、材料弹性模量以及截面积的大小计算得到的.各工况拉索动拉力幅值如表5、6所示.其中，Fmax为单根拉索动拉力幅值，μF为动拉力幅值与悬吊质量自重（245 N）的比值.索长为0.2 m时，钢索和弹簧动拉力时程见图10、11.

图10 钢索动拉力

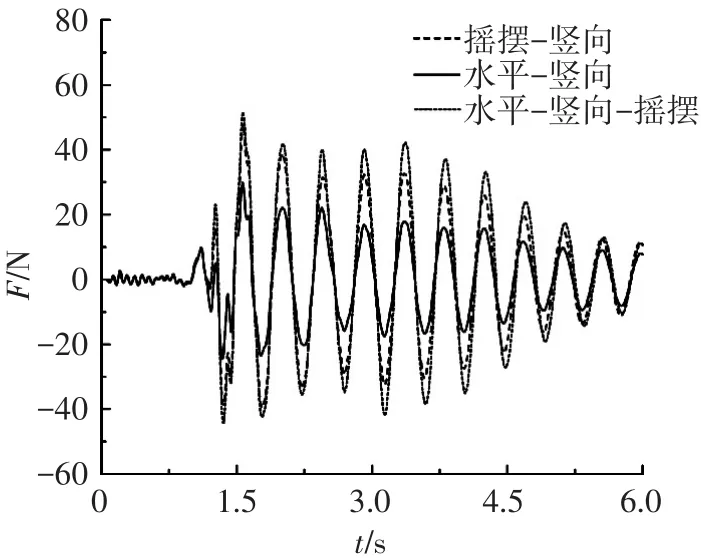
图11 弹簧动拉力

由表5、6和图10、11可以看出:1）当拉索为钢索时，由于有竖向地震作用，拉索动拉力幅值较大，超过悬吊质量自重.而拉索动拉力最大负值绝对值为245 N，即等于悬吊质量产生的静拉力，因此在某些微时间段，出现拉应力为零的状态.2）当拉索为弹簧时，拉索动拉力幅值较小，最大值仅为悬吊质量自重的21%，并随索长的增大而减小；3）在试验过程中可观测到，在各工况下，当拉索为弹簧时，悬吊质量在水平摆动的同时，还在以自己的频率上下振动.当拉索为钢索时，虽然出现拉应力为零的状态，但悬吊质量没有出现不规则振荡现象.

4 试验与理论结果对比分析

进行理论计算时，考虑到振动台实际输出和输入存在一定差异，因此在理论分析时，采用台面实测所得到的地震波时程，并将水平、竖向和摇摆地震波峰值按比例分别调整为6.2 m／s2、5.78 m／s2、0.246 rad／s2.

本文中结构动力方程采用层模型形式，因此将模型结构的质量和刚度简化为集中质量和整体抗侧刚度.计算模型中各几何尺寸与试验模型相同，弹簧长为0.2 m时理论分析与试验结果对比见表7.表中T为与结构主体水平振型相对应的第1周期．aH+V、aT+V、aH+V+T、wH+V、wT+V、wH+V+T、FH+V、FT+V、FH+V+T分别为在地震动水平-竖向、摇摆-竖向和水平-竖向-摇摆耦合作用下的框架顶层水平加速度、位移和拉索动拉力幅值．

当拉索为钢索时，理论分析中的索拉力出现负值，与实际情况不符，动力方程式（3）不再适用，必须采用更进一步的非线性动力方程分析.当拉索为弹簧时，索拉力始终为拉力，适用于本文推导的动力方程.由表3可知:1）框架顶层水平加速度幅值的理论分析与试验结果最大误差为9%，位移幅值的为21%，后者的误差较大，这可能是由于试验结果的位移时程是根据实际记录的加速度（速度）时程积分得到的，易受试验中噪声干扰；2）理论分析的拉索动拉力幅值均大于试验值，主要原因可能是理论分析时，横梁刚度假设为无限大，而与实际模型有区别；3）理论计算和试验结果的变化趋势基本一致.

综上可得，当悬吊质量作为质量摆减震系统时，采用钢索和弹簧对于结构加速度和位移响应的减震效果相近，而钢索的动拉力幅值较大，弹簧的却小很多，因此应尽量采用弹簧或拉压刚度较小的构件.

上述结果是对一个近震的实际地震波（摇摆地震波通常近震时比较显著）作用下的某一特定结构进行研究得到的结论，但在实际工程中，悬吊质量对主体结构的动力效应与主体结构的刚度、悬吊质量动力参数以及地震波的卓越频率均有关，因此，具有悬吊质量结构体系的抗震设计方案应根据实际情况进行分析.另外，本文是采用Northridge地震中Pacoima大坝左上侧站点记录的地震波时程对结构的动力效应进行分析的，而该站点由于地震倾斜转角加速度和位移幅值较大（残余倾斜约为0.04 rad），因此所得到的结果中摇摆分量产生的动力效应所占比重也相对较大.

表7 理论分析与试验结果对比

5 结 论

1）相较于水平地震动作用，悬吊质量对摇摆地震动作用下主体结构的动力响应影响更加明显；在摇摆-竖向分量作用下，当索长为0.2 m时，无论拉索是钢索还是弹簧，结构顶层加速度和位移减震效果均可达13%以上，且随着索长的增加，减震效果降低；在水平-竖向-摇摆耦合作用下，由于包含了摇摆地震动，索长对结构顶层最大加速度和位移幅值的影响仍较大；索长变化使水平位移幅值变化的程度大于使水平加速度幅值变化的程度.

2）当拉索为钢索时，由于有竖向地震作用，其动拉力幅值较大，超过了悬吊质量自重.而在某些微时间段，会出现拉应力为零的状态，在实际工程设计中，应予以重视；当拉索为弹簧时，其动拉力幅值较小，最大值仅为悬吊质量自重的21%，并随着索长的增大而减小.

3）将拉索由钢索改为同等长度的弹簧后，结构顶层的加速度响应和位移响应变化不大，但拉索动拉力却明显减小.因此当采用悬吊质量作为质量摆减震系统时，拉索应尽量采用弹簧或拉压刚度较低的构件.

［1］李宏男.摆—结构体系减震性能研究［J］.工程力学，1996，13（3）:123-129.

［2］GRAIZER V M.Effect of tilt on ground motion data processing［J］.SoilDynamicsandEarthquake Engineering，2004，25（3）:197-204.

［3］KALKAN E，GRAIZER V.Multi-component ground motion response spectra for coupled horizontal，vertical，angularaccelerations，andtilt［J］.Journalof Earthquake Technology，2007，44（22）:1-33.

［4］GRAIZER V，KALKAN E.Response of pendulums to complex input ground motion［J］.Soil Dynamics and Earthquake Engineering，2008，28（8）:621-631.

［5］KALKAN E，GRAIZER V.Coupled tilt and translational ground motionresponsespectra［J］.Journalof Structural Engineering，2007，133（5）:609-619.

［6］LI Hongnan，SUN Liye，WANG Suyan.Improved approach for obtaining rotational components of seismic motion［J］.Nuclear Engineering and Design，2004，232（2）:990-137.

［7］LEE V W，TRIFUNAC M D.Rocking strong earthquake accelerations［J］.Soil Dyn Earthquake Eng，1987，6（2）:75-89.

［8］DHIMAN B，ANDREW W S，MICHAEL C C. Estimating rotational components of ground motion using data recorded at a single station［J］.Seismological Research Letters，2013，84（1）:130-138.

［9］EMMANUEL J H，TATSYO O.Estimation small permanent rotation from strong-motion records:What is comparison with external measurements telling us？［J］. Bull Seism Soc Am，2012，102（5）:2257-2263.

［10］李宏男，王前信.水平与摇摆地震动作用下大跨越输电塔体系的反应分析［J］.工程力学，1991，8（4）:68-79.

［11］李宏男，王苏岩，周健.在水平与摇摆地震动联合作用下高层与高耸结构随机反应分析［J］.土木工程学报，1991（1）:44-51.

［12］陆铁坚，李芳，余志武.在地震动水平与摇摆分量作用下高层结构随机地震反应［J］.中南大学学报:自然科学版，2006，37（3）:623-627.

［13］李宏男.结构多维抗震理论设计方法［M］.北京:科学出版社，1998.

［14］SINAN A，MATTHEW D J.The rocking response of large flexible structures to earthquakes［J］.Bulletin of Earthquake Engineering，2014，12（2）:875-908.

（编辑 魏希柱）

Seismic response of structure with suspended mass

WEI Wenhui，ZHANGD Di，YU Meng，WU Qiwei
（Hubei Key Lab of Road Bridge and Structure Engineering，Wuhan University of Technology，430070 Wuhan，China）

To study the dynamic response of the structure with suspended mass under coupled horizontal，vertical and tilt ground motions，the dynamic equation of the structure under coupled horizontal，vertical and tilt ground motions was derived.A modified method was proposed to obtain the tilt component.Taking a valve hall with suspended mass as prototype，the shaking table test of a 1∶10 scale model was carried out，and the seismic responses of structure under coupled horizontal-vertical，tilt-vertical and horizontal-vertical-tilt when different lengths of steel cable and spring to hang the mass.The results show that，compared with under horizontal component，the damping effect of suspended mass on main structure under tilt component is more obvious.The damping effect of suspended mass on main structure decrease as the length of steel cable or spring grows.When using spring of the same length to replace steel cable，the changes in acceleration and displacement on the top of structure are not big，but the dynamic tension of cable decreases.Thus，when suspended mass is used as damping system，the cable should employ spring or the member with low axial rigidity.

susmic response；suspension system；ground motion；tilt ground motion；shaking table test

TU311.3

A

0367-6234（2014）04-0098-07

2013-04-19.

国家自然科学基金资助项目（51178362）.

魏文晖（1963—），男，教授.

魏文晖，weiwenhui＠whut.edu.cn.