基于自适应陷波滤波器的在线机械谐振抑制

杨 明，郝 亮，徐殿国

基于自适应陷波滤波器的在线机械谐振抑制

杨 明，郝 亮，徐殿国

（哈尔滨工业大学电气工程及自动化学院，150001哈尔滨）

针对不断拓展的伺服系统带宽将会超过系统固有机械谐振频率而引发机械谐振，克服原本被忽略的弹性部件的影响以提高伺服系统性能，采用自适应陷波滤波器进行在线机械谐振抑制.首先对双惯量弹性负载模型进行理论分析，解释及验证了机械谐振机理及现象.通过FFT法实时分析电磁转矩电流，可以在线快速辨识机械谐振特性，并以此辨识结果在线自动整定陷波滤波器参数，快速有效地抑制机械谐振.实验结果表明，该方案能够在线自动抑制弹性负载引起的谐振问题.离散化的高刚度谐振系统将以自然谐振频率持续振荡，而在线自适应滤波器无需对控制器参数进行改变，即可满足系统高刚度控制的同时抑制谐振.

伺服系统；弹性负载；在线机械谐振抑制；陷波滤波器；FFT

伺服驱动系统的机械传动部分经常使用传动轴、变速器、联轴器等传动装置连接电机和负载.而实际传动装置并不是理想刚体，存在一定的弹性，通常会在系统中引发机械谐振［1］.由于伺服系统动态性能的不断提升，原本被忽略的传动装置中弹性部件的影响越发显著.特别针对中高压大功率电机驱动系统，如果谐振抑制不当将产生断轴等严重事故，后果不言而喻.因此，机械振荡的研究以及抑制方法已经成为提高伺服驱动系统性能的一个重要课题.

早期避免机械谐振的方法很简单，就是降低速度给定的阶跃值或变化斜率，但这必然会限制系统的频响带宽［2］.目前各种研究方案主要针对仅测量驱动电机侧的位置、转速信息，传动装置及负载侧无需增加传感器.众多的研究方案可大致分为两类:被动方式和主动方式.

主动方式就是主动改变控制器参数或控制器结构用以消除谐振影响.主动方式可分为单纯PI控制（双自由度PI控制、RRC）［3-4］、基于PI的状态反馈控制［5-6］、其他高级算法应用［7-9］等多种方案.

被动方式就是在速度环输出与电流环给定之间插入陷波滤波器，而控制系统其他设计不变.利用陷波滤波器衰减指定频率的幅值而对其他频率没有影响的特点，而且其参数设计物理概念明确、简单易行，串入多个陷波滤波器即可抑制多个谐振频率，是目前大规模商用伺服系统普遍采用的方案［10-12］.但这种方法需要高效的谐振频谱辨识方法来准确辨识谐振频率.离线抑制方式首先要通过扫频或其他方法获得系统Bode图，然后通过分析谐振频率特性来设置滤波器参数.这种方法需要占用很多时间而且还要额外运行一次系统.文献［13］详细阐述了定点算法中所遇到的如延时、量化误差等各种数字信号处理问题.陷波滤波器的通带范围过宽会导致较大的相角滞后，为了增加抑制深度而采用窄通带设计又导致受谐振频带辨识影响加剧，因此，文献［14］采用自适应陷波滤波器设计方案，该方案能够快速辨识谐振中心频率并以此调整滤波器参数设计.尽管陷波滤波器的零极点数目相等对通带范围造成的相角滞后较小，但还是附加了相角滞后，文献［15］通过相角补偿追求零相位滞后，取得一定的效果.而文献［16］引入一FIR滤波器代替传统陷波滤波器，并且只需调整1个参数即可实现，但受谐振辨识影响巨大而且不能消除多个谐振点，因此实际抑制效果一般.

本文深入分析离散化后谐振系统的振荡情况，并提出了一种在永磁交流伺服系统中的在线机械谐振抑制方法.通过FFT的辨识结果自动设置陷波滤波器的参数.这种方法能够抑制系统稳态阶段由控制器饱和而激发的持续振荡.首先分析谐振机理，尤其对离散化后高刚度系统的谐振进行研究；通过采用FFT直接分析转矩电流的方法，系统的谐振频率可以在线辨识出来.基于谐振特性的辨识结果系统自动设置陷波滤波器的参数.仿真及实验的结果表明，该算法可以保证系统高刚度控制的同时在线准确获取系统的谐振频率及谐振幅值，并自动整定陷波滤波器来有效抑制机械谐振.

1 机械谐振的建模与分析

1.1 机械谐振的建模

在实际系统中，传动装置的刚度是有限制的，并具有一定弹性.每个机械装置都有自己的弹性及谐振频率.通常传动装置引起的机械谐振频率集中在100～2 000 Hz之间［17］，如图1所示.

图1 不同因素引起的机械谐振

电机、传动机构、执行机构组成的典型双惯量机械传动系统如图2所示．电机和执行机构通过传动轴系联接，传动轴系具有一定的抗扭刚度K和阻尼系数Cw．当传动轴系发生扭转形变时轴系将产生转矩Tw，此转矩对于电机来说可看作是电机的负载转矩，而对于执行机构来说可看作是驱动转矩．伺服驱动器控制电机运行，为电机的转轴提供电磁转矩Te．在电机端电磁转矩Te和传动轴系转矩Tw作用于转动惯量为J1、阻尼系数为C1的电机转轴．在执行机构端，执行机构具有大小为J2的等效转动惯量以及阻尼系数C2，传动轴系转矩Tw与负载转矩Tl共同作用于执行机构最终决定了负载转速．根据以上分析可建立微分方程组．

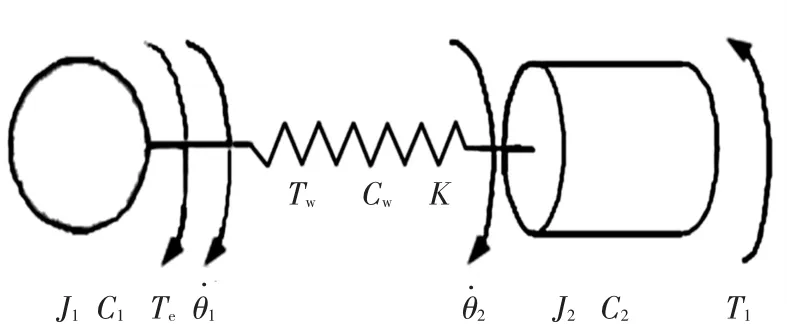
图2 典型双惯量机械传动装置模型

由于系统中的阻尼系数很小，可忽略阻尼系数从而对系统模型进行化简.对化简后的系统微分方程组进行拉普拉斯变换，得

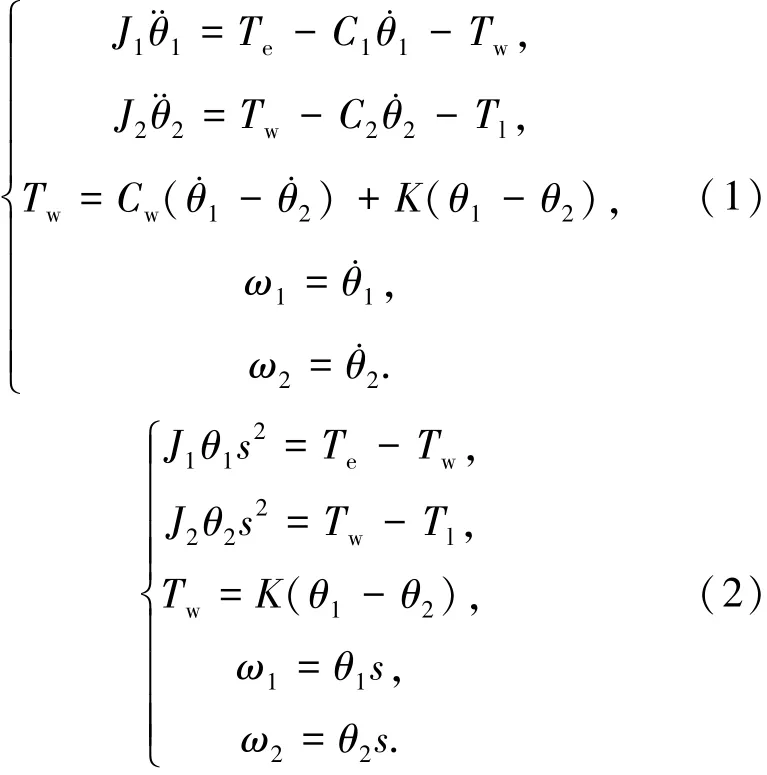
根据式（2）可推导出如图3所示的机械传动装置模型框图，进而推导出电机转速与电机电磁转矩之间的传递函数为

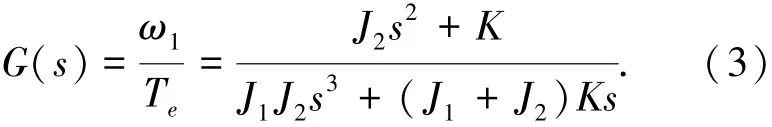
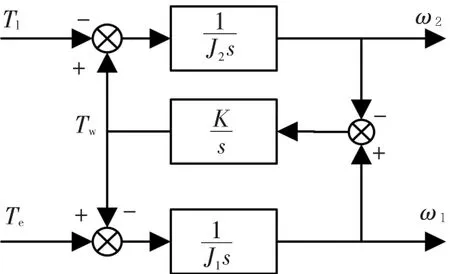
图3 传动装置模型框图

从式（3）可以得出，机械谐振点在传递函数上引入了一对共轭的零极点，共轭零点为抗谐振频率点ARF（anti-resonance frequency），共轭极点为自然振动频率点NTF（naturaltorsional frequency）.零极点的存在使得系统在特定频率下的响应会比较强烈，这就会形成机械谐振现象.通过式（3）可以得到两个谐振点具体频率及惯量比R的关系为

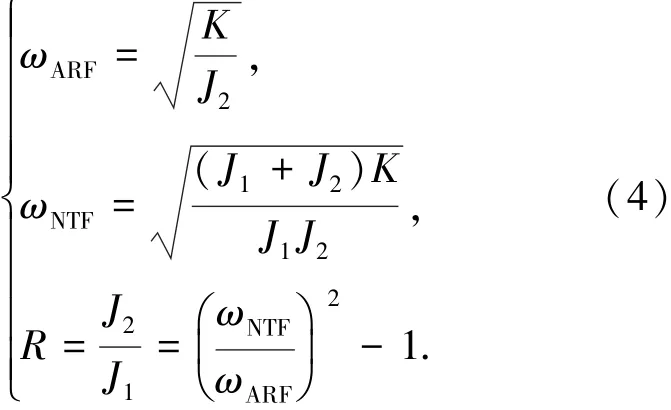
1.2 机械谐振的影响及特性

跟理想刚性传动装置相比，实际传动装置中电机转速受闭环控制基本稳定，但负载转速以及电机电磁转矩都出现严重振荡.

图4为传动轴系中的电机与负载间的转速差振荡仿真结果.扭转振荡的存在会损害机械传动装置，降低使用寿命.

图4 扭转振荡的仿真结果

从图4可以看出，振荡频率明显分为两段:当速度调节器饱和，系统处于速度控制开环阶段，此时电机和负载侧都以NTF频率振荡；当电机速度达到给定速度，速度调节器退饱和，进入速度控制闭环阶段，电机和负载速度振荡频率为ARF频率.

此外，由于实际伺服驱动系统均是数字化控制系统，所以也要考虑离散对系统谐振现象的影响.离散后系统稳定裕度减小，甚至会发生失稳.在这里用增益裕度GM来表示，在速度开环情况下，速度控制器比例增益Kp决定增益裕度.当GM小于零，闭环离散系统发散.图5是两种Kp情况下的速度开环Bode图.

图5 不同Kp的开环离散系统Bode图

离散系统和机械谐振的共同影响会使系统在原本稳定范围的Kp下就会发生振荡现象；但由于受到速度调节器的饱和限幅，使得系统持续稳定的振荡．稳定裕度的降低而导致稳定振荡的主要因素有两点:离散化及谐振特性．

图6表示的是在不同采样频率下的谐振系统的电机阶跃时的谐振现象，可以发现采样频率较低的离散系统在刚度较大的情况下会发生持续振荡的频率，该频率已不是ARF谐振频率.

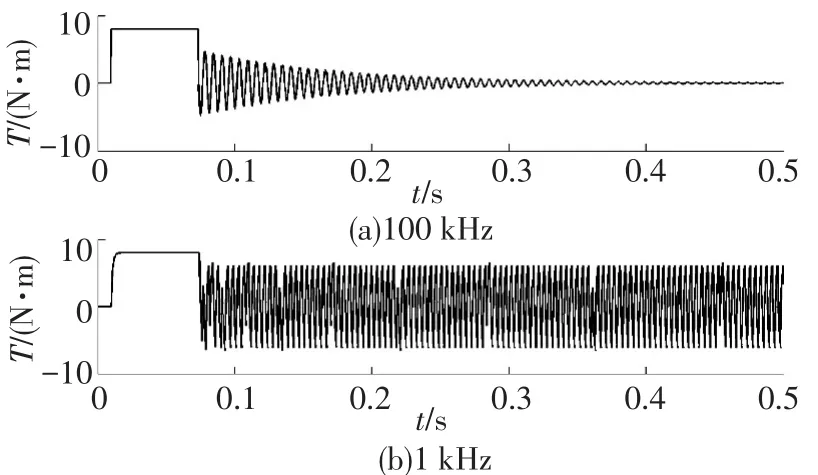
图6 不同采样频率的影响

这种持续振荡的频率才是在线谐振抑制的主要频率.图7为不同离散化频率时的对转速差的FFT分解.从图7中可以看出，不同采样频率下都会有NTF的谐振频率存在，而且附加的频率为fs／2．（此样例中设定fNTF=140 Hz）由于数据保持原理，实际系统在采样后会有一个低通滤波器进行滤波，所以在实际中的该情况下只体现NTF谐振频率.

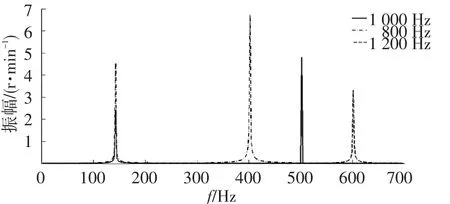
图7 不同采样频率对谐振频率成分的影响

所以通过上述分析可知，对于实际数字化控制系统，在刚度较高的情况下，无论暂态还是稳态都以NTF频率在谐振.

2 机械谐振的在线抑制

2.1 陷波滤波器的设计

常规的速度控制器即便实现最优自整定参数也只能做到消除系统固有主导极点，并不能消除由机械谐振引起的欠阻尼振荡极点，所以需要采用陷波滤波器的方式来消除系统中的谐振极点，谐振系统根轨迹见图8，其中电流内环简化成一阶惯性环节.陷波滤波器的设计主要是通过自身零点对消谐振引入的主导共轭极点.

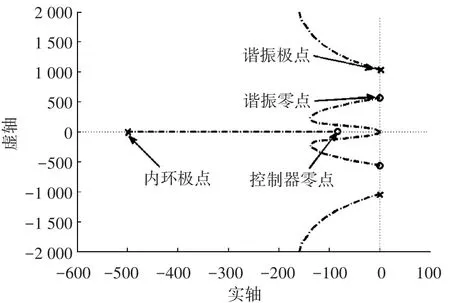
图8 谐振系统根轨迹

为了能方便地对陷波滤波器的作用频率、陷波带宽以及陷波深度进行调节，可以选用改进型双T网络陷波滤波器.图9是传统陷波滤波器与改进型陷波滤波器的对比.从图9可以看出，与传统陷波滤波器相比，改进型陷波滤波器在作用频率前的衰减要缓慢.

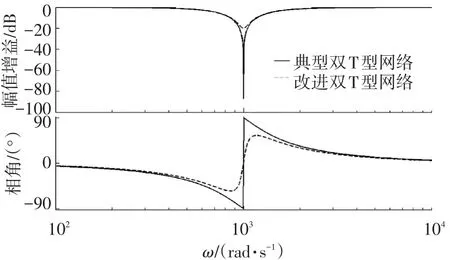
图9 两种滤波器的对比

改进型陷波滤波器的传递函数为

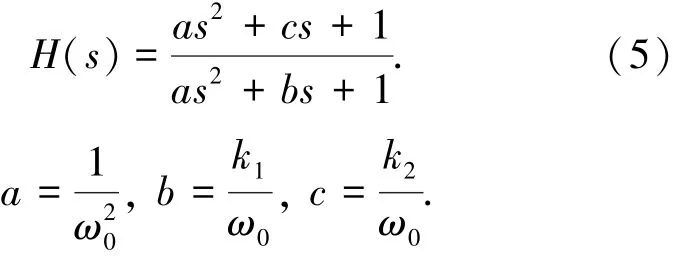
根据滤波器作用的频率点ω0、陷波带宽参数k1以及陷波深度参数k23个变量可决定滤波器的a、b、c 3个系数．式（6）表示的是陷波带宽Bw以及陷波深度Dp与系数k1和k2之间的关系.

通过调节陷波频率ω0改变陷波滤波器的零点，来对消系统的谐振极点．可以通过调节陷波带宽k1来调整附加极点的位置，当k1=2时，附加极点会全部在实轴上，根轨迹见图10．

图11表示的是不同参数的变化对滤波器的影响.从图11（b）、11（c）可以看出，过大的陷波带宽及过深的陷波深度会导致ω0附近其他频率信号的相角滞后（超前）现象加剧.所以在保证滤波带宽以及深度足够的情况下，尽可能减小滤波带宽和深度，从而降低相频特性的恶化.

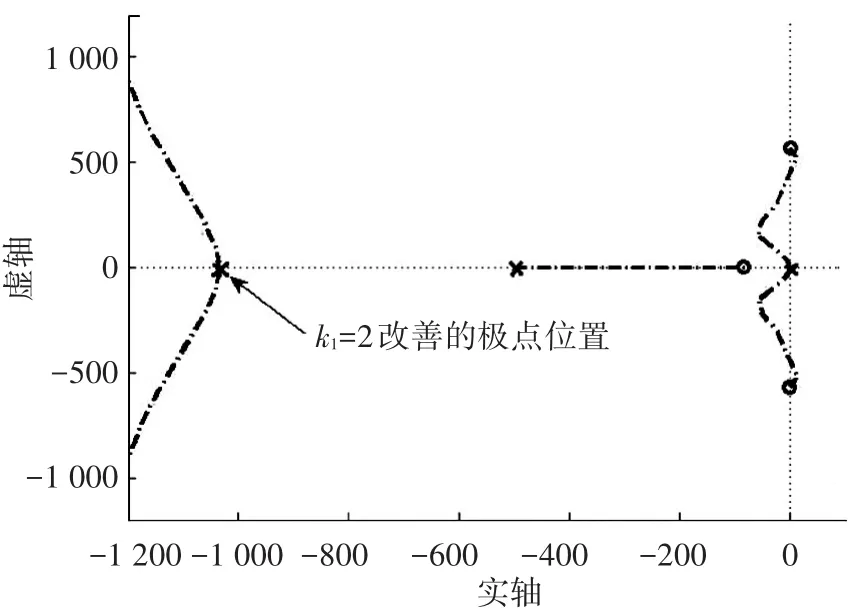
图10 k1=2时的系统根轨迹

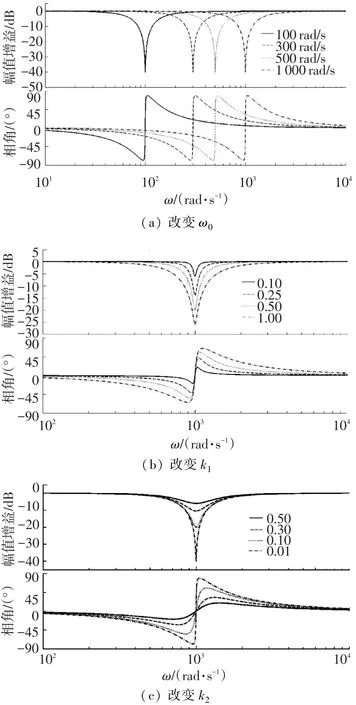
图11 不同滤波器参数的影响

将陷波滤波器串入速度环控制环路中，对转速调节器输出的电流环给定信号进行滤波，抑制电机电流的振荡，进而对电机输出电磁力矩产生抑制，最终达到抑制机械谐振的目的．在设计滤波器参数时，应首先确定系统的谐振频率ω0．之后针对谐振频率确定其陷波带宽参数k1和陷波深度k2．

2.2 频率特性的在线辨识

本文主要研究的是基于频率抽取算法的快速傅里叶变换.通过图蝶形算法原理，实现基于频率抽取算法的快速傅里叶变换，完成信号的分析.

在实际的数字控制系统中，采样结果可以看成有限长非周期序列x［n］，序列x［n］及其傅里叶频谱X［k］的变换式分别为

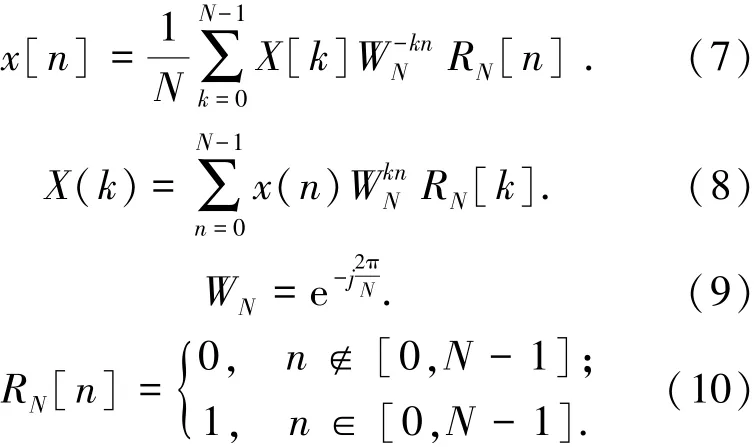
可以推导出，离散傅里叶变换形式为

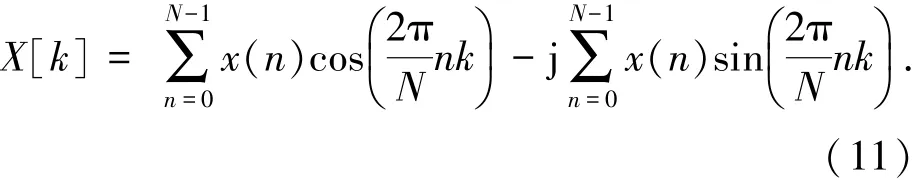
单个快速傅里叶变换运算单元运算表达式为

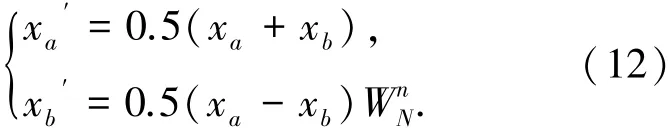
但此时的频谱存储序列X［k］需要重新按位倒序放置．根据采样定理，如果信号的频谱最高频率为fmax，为了保证频谱分析结果不发生频谱混叠，采样频率fs不能小于最高频率fmax的2倍．变换后的频谱X［k］点数为N，则X［0］至X［N／2］表示［0，fs／2］频率区间内的信号离散频谱．

在永磁交流伺服系统中，经常采用的是磁场定向控制（FOC）.在矢量控制中，将电机定子绕组电流转化为转子旋转轴系下的交轴电流以及直轴电流.其中，直轴电流表示电机电流的励磁分量，交轴电流表示电机电流的转矩分量.也就是说，在对电机电流进行矢量解耦之后，交轴电流仅与电机的输出转矩有关，二者呈线性关系.由于机械谐振引发了电机转速振荡以及转矩的振荡，因此通过直接分析电机的交轴电流，即可分析电机转矩的频率特征，进而分析系统的频率特征.该在线辨识算法只需要对交轴电流进行采样分析，运算量小，运算速度快，能够直接反应出系统中存在的机械谐振现象.图12是机械谐振抑制结构框图.

在线机械谐振抑制主要有采样，计算，获取谐振点，计算谐振频率4步.启动机械谐振自动抑制功能后，开始对进入稳态的交轴电流信号进行采样.每一个速度环采样周期完成一次交轴电流信号采样，把每次采样数据存储到寄存器中等待整体计算.当采样点数达到快速傅里叶运算预定的点数时，采样结束并开始进行FFT蝶形运算.获取谐振点需要排除低频段的频谱数据并分析最为可能的极值点信息来自动配置陷波滤波器.

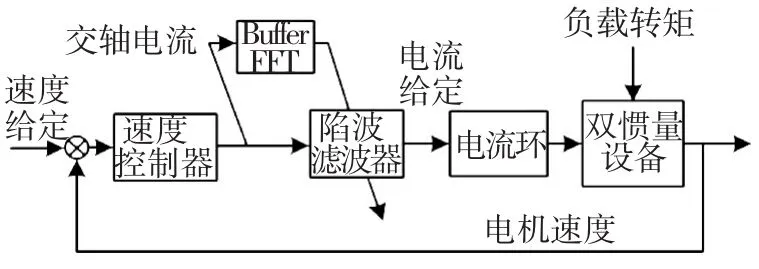
图12 在线机械谐振抑制结构框图

3 仿真与实验

3.1 仿真结果

仿真及实物实验中所使用的永磁同步伺服系统的参数如下:额定功率为0.75 kW，额定转矩为2.39 N·m，额定电流为4 A，电机惯量为11.0× 10-4N·m2，传动轴弹性系数为560 N·m·rad-1.令系统的负载转矩类型为摩擦型转矩，大小为1 N·m.系统给定信号为2 000 r／min的阶跃.

图13表示的是对离散系统机械谐振现象及其抑制的仿真图.采用的方法是在线FFT辨识并自动配置滤波器.图13（a）、13（b）分别为滤波前后电机转速与负载转速的阶跃响应曲线.可以看出经过滤波后，电机转速的振荡受到抑制.图13（c）中，滤波前后电机阶跃响应的电磁转矩曲线也表明滤波器抑制了电机交轴电流中的振荡，进而抑制了电机电磁转矩的振荡，最终实现机械谐振的抑制［18］.

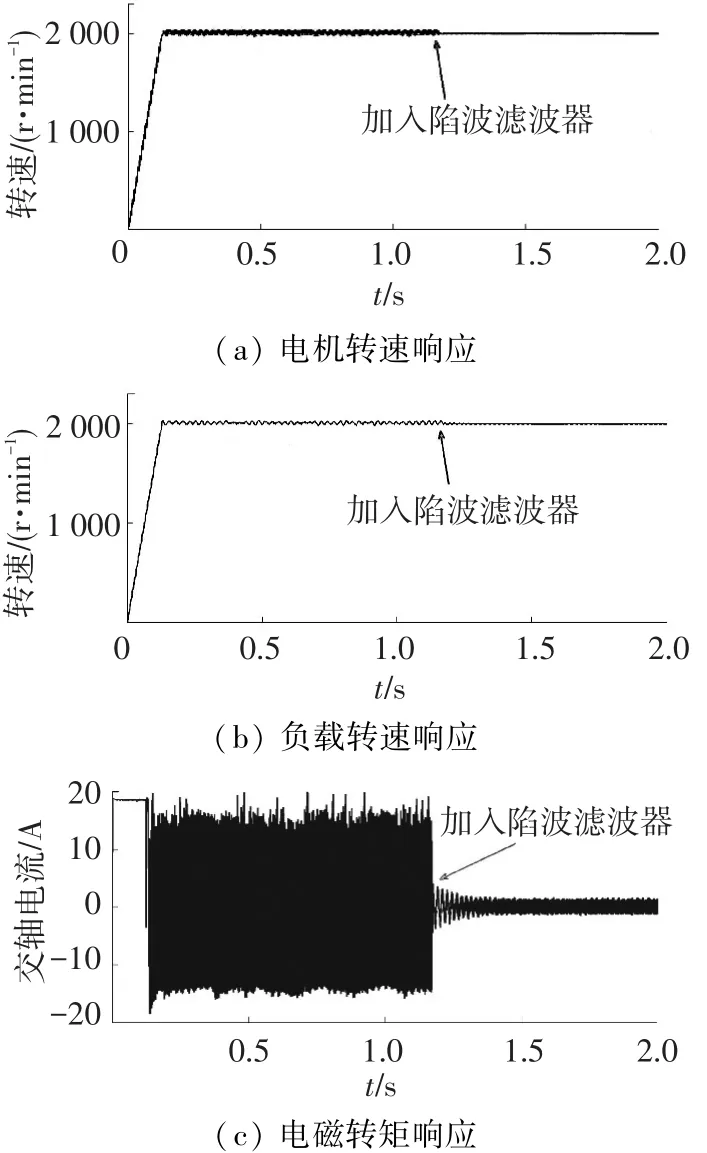
图13 机械谐振抑制仿真结果

3.2 实验结果

机械谐振抑制平台实物照片如图14所示.左侧是实验室的电机及750 W伺服驱动器，右侧是作为对比及负载的电机.在电机与负载间有一根可以产生机械谐振的传动轴.谐振频率可以通过附加惯量盘或更换其他传动轴的方法改变.控制器核心芯片为TMS320F2812.

图14 双惯量系统实物照片

由于采样频率为1 kHz，系统可以获得的频率为0～500 Hz.越多的采样点数，谐振频率的分析精度就越高，但数据需要的存储空间及程序运行时间就越长.最终选择1 024点的采样点数.图15表示的是系统在稳态振荡中的交轴电流的FFT分析结果.在线计算的总时长为1 087 ms.图16为开启自整定陷波滤波器的速度阶跃的现象.

图15 交轴电流FFT分析结果

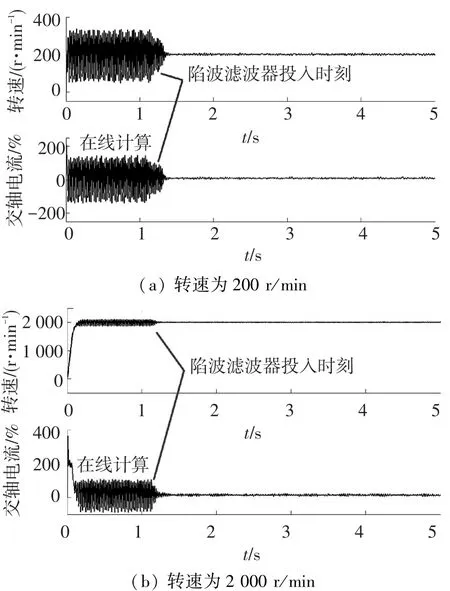
图16 在线抑制机械谐振实验波形

图16（a）为200 r／min下的转速及交轴电流结果，图16（b）为2 000 r／min下的转速及交轴电流结果.从图15可以看出，分析出的161 Hz的谐振频率与图16的时域结果吻合.无论速度给定的阶跃值如何，只要控制器刚度覆盖自然谐振频率，系统就会产生持续振荡.通过采样和FFT分析，自动辨识的数据输入给陷波滤波器，系统开启抑制功能.可以看出开启在线自整定滤波器后的抑制效果明显，系统保持了高刚度控制的同时，能够有效地抑制机械谐振.

4 结 论

1）重点分析了离散系统的谐振状况，并提出了一种基于自适应陷波滤波器的在线机械谐振抑制方法.

2）分析了带弹性传动装置的双惯量系统机械谐振的模型与机理.暂态系统谐振频率为NTF；连续系统速度控制闭环状态下的谐振频率为ARF；离散系统中，如果控制系统的刚度大，由于谐振特性和速度控制器饱和的影响，系统会以NTF频率在稳态持续振荡.

3）采用FFT技术在线分析出谐振特征可以不用考虑是何种类型的谐振频率.根据谐振特征的辨识结果在线自动整定陷波滤波器参数.仿真及实验结果证实了该在线自适应滤波器可保证高刚度控制的同时自动抑制机械谐振.

［1］马小亮.驱动弹性负载的调速传动［J］.电气传动，2008，38（7）:3-7.

［2］MURPHY B R，WDTANABE I.Digital shaping filters for reducing machine vibration［J］.IEEE Trans Robot and Auto，1992，8（2）:285-289.

［3］KATSURA S，OHNISHI K.Force servoing by flexible manipulator based on resonance ratio control［J］.IEEE Trans on Industrial Electronics，2007，54（1）:539-547.

［4］MUSZYNSKI R，DESKUR J.Damping of torsional vibrations in high-dynamic industrial drives［J］.IEEE Trans on Industrial Electronics，2010，57（2）:544-552.

［5］SZABAT K，ORLOWSKA-KOWALSKA T.Vibration suppression in a two-mass drive system using PI speed controller and additional feedbacks:comparative study［J］.IEEE Trans on Industrial Electronics，2007，54（2）:1193-1206.

［6］ORLOWSKA-KOWALSKA T，KAMINSKI M.Effectiveness of saliency-based methods in optimization of neural state estimators of the drive system with elastic couplings［J］. IEEE Trans on Industrial Electronics，2009，56（10）: 4043-4051.

［7］HACE A，JEZERNIK K，ŠABANOVIC A.SMC with disturbance observer for a linear belt drive［J］.IEEE Trans on Industrial Electronics，2007，54（6）:3402-3412.

［8］PETER K，SCHÖLING I，ORLIK B.Robust outputfeedback H∞-control with a nonlinear observer for a twomass system［J］.IEEE Trans on Industry Applications，2003，39（3）:637-644.

［9］CYCHOWSKI M，SZABAT K，ORLOWSKA-KOWALSKA T.Constrained model predictive control of the drive system with mechanical elasticity［J］.IEEE Trans on Industry Applications，2009，56（6）:1963-1973.

［10］ELLIS G，LORENZ R D.Resonant load control methods forindustrialservodrives［C］／／2000Industry Applications Conference.Rome:IAS，2000:1438-1445.

［11］HSU W C，LAI C L，HSU P L.A novel design for vibration suppression for lightly-damped servo control systems［C］／／Proceedings of 2011 8th Asian Control Conference.Kaohsiung:IEEE ASCC，2011:251-256.

［12］SCHMIDT P，REHM T.Notch filter tuning for resonant frequency reduction in dual inertia systems［C］／／Industry Applications Conference 1999.Proenix:IEEE IAS，1999:1730-1734.

［13］HARNEFORS L.Implementation of resonant controllers and filters in fixed-point arithmetic［J］.IEEE Trans on Industrial Electronics，2009，56（4）:1273-1281.

［14］KANG C I，KIM C H.An adaptive notch filter for suppressing mechanical resonance in high track density disk drives［J］.Microsystem Technologies，2005，11: 638-652.

［15］KUMAGAIS，OHISHIK，MIYAZAKIT.High performance robot motion control based on zero phase error notch filter and D-PD Control［C］／／Proceedings ofthe2009IEEEInternationalConferenceon Mechatronics.Malaga:ICM，2009:1-6.

［16］VUKOSAVIC S N，STOJIC M R.Suppression of torsional oscillations in a high-performance speed servo drive［J］.IEEE Trans on Industrial Electronics，1998，45（1）:108-117.

［17］OHISHI K.Robust position servo system based on vibrationsuppressioncontrolforindustrialrobotics［C］／／The2010InternationalPowerElectronics Conference.Sapporo:IEEE IPEC，2010:2230-2237.

［18］杨明，胡浩，徐殿国.永磁交流伺服系统机械谐振成因及其抑制［J］.电机与控制学报，2012，16（1）: 79-84.

（编辑 魏希柱）

Online suppression of mechanical resonance based on adapting notch filter

YANG Ming，HAO Liang，XU Dianguo
（School of Electrical Engineering and Automation，Harbin Institute of Technology，150001 Harbin，China）

To improve the performance of servo system，online suppression of mechanical resonance based on adapting notch filter is adopted.The expansion of bandwidth in servo system will exceed the natural mechanical resonance frequency.The originally ignored influence of elastic components will be more obvious，and mechanical resonance is caused.Firstly，the theoretical analysis of 2-mass model with elasticity load is carried out.The results of simulation verify this resonance mechanism and phenomenon.By FFT method to real-time analyze the electromagnetic torque current，resonance characteristic can be identified online and quickly. Based on identification result of resonance characteristic，parameters of notch filter can be online-set automatically.It can suppress mechanical resonance quickly and effectively.Experiment results show this method can online-suppress the resonance caused by elastic load automatically.Resonance system with high stiffness sustained oscillates at natural torsional frequency when the system is discretized.This method which uses adapting filter to suppress mechanical resonance doesn’t need to change the parameters of controller while high stiffness of control is satisfied.

servo system；torsional load；online suppression of mechanical resonance；notch filter；FFT

TM921

A

0367-6234（2014）04-0063-07

2013-05-15.

国家自然科学基金资助项目（61273147）；

台达环境与教育基金会资助项目（DREK2012002）.

杨 明（1978—），男，博士，副教授；

徐殿国（1960—），男，教授，博士生导师.

杨 明，yangming＠hit.edu.cn.