适用于高温阻抗管的修正传递函数法

张哲，王小鹏，陈天宁，奚延辉

（1.西安交通大学机械工程学院，710049，西安；

2.西安交通大学机械结构强度与振动国家重点实验室，710049，西安）

金属多孔材料在新型汽车、高速列车、航空航天器等高能耗装备的消声降噪技术中均具有重要的应用价值［1－3］。目前，多孔金属材料的吸声性能研究大多在常温常压条件下进行，而对高温或材料前、后端面间有温度梯度条件下的吸声性能研究则相对不足［4］，国内外已发表的相关研究成果寥寥无几，其中一个主要原因是缺少相应的测试技术。由于目前市场上没有可以工作在高温环境（高于150℃）的扬声器，因此在用阻抗管测量吸声材料高温吸声系数时，总是扬声器处于低温，而吸声材料处于高温，从而在阻抗管内的空气中形成了温度梯度。传统的传递函数要求阻抗管内空气温度均匀［5］，因此当阻抗管内存在温度梯度时，就必须考虑能否继续应用传递函数法测量吸声系数。冯凯、薛昌意等分别设计了高温、温度梯度阻抗管［6－7］，但是由于管径较小、管长较大且一端封闭，使温度测量较为困难，导致测量结果误差较大，误认为管内温度符合传递函数法的均温要求，因而没有对阻抗管内部能否产生平面波进行验证。本文利用自制的温度传感器支架得到阻抗管内的准确温度，对自制阻抗管内能否产生平面波进行校核，同时考虑轴向温度梯度的影响对传统传递函数法进行修正，以期为高温环境下传递函数法的使用提供理论基础。

1 高温阻抗管中平面波的产生条件

只有当阻抗管内传播平面波时，才可以用传声器测点处的声压值来代表整个波的能量，否则每点声压值不同，将使得测量失去意义。因此，传递函数法应用于高温阻抗管的要求依然是管中要能产生平面波。现已知阻抗管中的空气有温度梯度，那么该温度梯度能否产生平面波？这是本文首先要解决的问题。首先对自制的高温阻抗管进行温度场仿真，并与实验测量值进行比较，得到一个准确的温度场，然后将该温度场导入comsol软件中进行仿真，以验证在该温度场下阻抗管中能否产生平面波，并且探索产生平面波的条件。

1.1 高温阻抗管温度场分析

自制高温阻抗管的原理图如图1［7］所示。该装置是在传统阻抗管上集成了加热装置的结果。从图1可以看出，加热方案是在材料后端面加热（右热源），在材料前端面周向进行水冷，以便在材料两端形成温度梯度，并且在材料前端一段阻抗管上进行加热保温（左热源）。本文仅考虑材料在高温环境下材料前端空气的温度分布，并未考虑材料两端温度梯度的实现，因此在仿真和实验中均不考虑水冷。

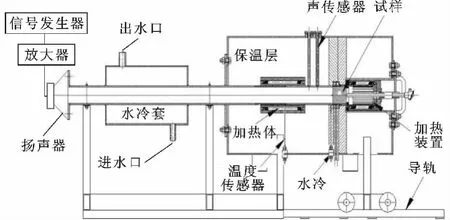
图1 自制高温阻抗管原理图

阻抗管的内径为50mm，壁厚为3mm，多孔材料厚度为50mm，较近的传声器距多孔材料前端面50mm，较远的传声器距材料前端面80mm，其他结构参数可参考文献［7］。分析可知阻抗管内部的空气产生了自然对流换热，因此，采用Fluent软件对阻抗管内的温度场进行仿真分析。首先对模型进行简化，由于对称性取阻抗管的一半进行分析，用ICEM CFD软件对其进行结构网格划分，网格数为65 529，并给定各边界条件，最终的计算模型如图2所示，各部件的物性参数见表1，阻抗管中的空气为不可压缩理想气体。

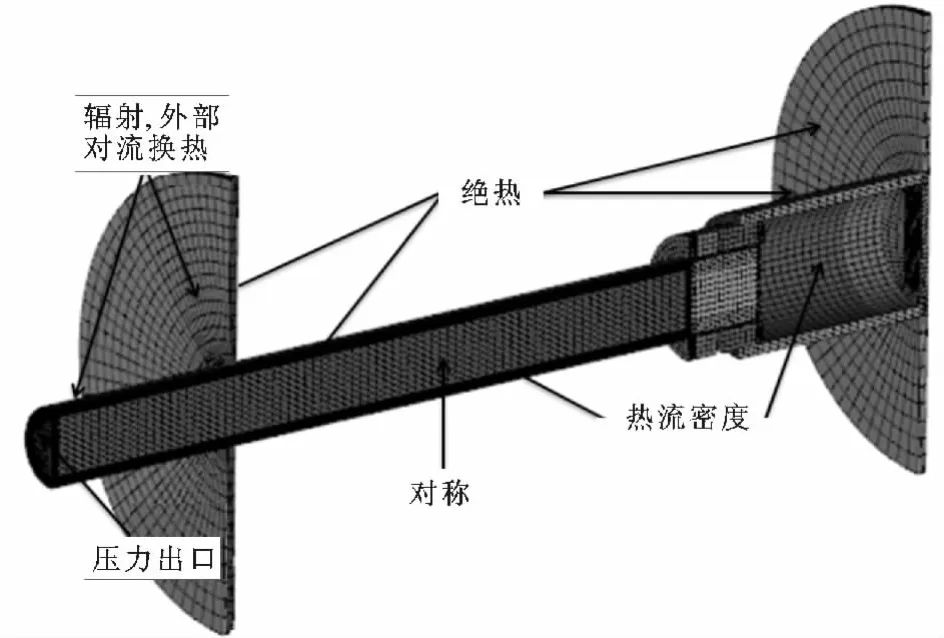
图2 Fluent计算模型

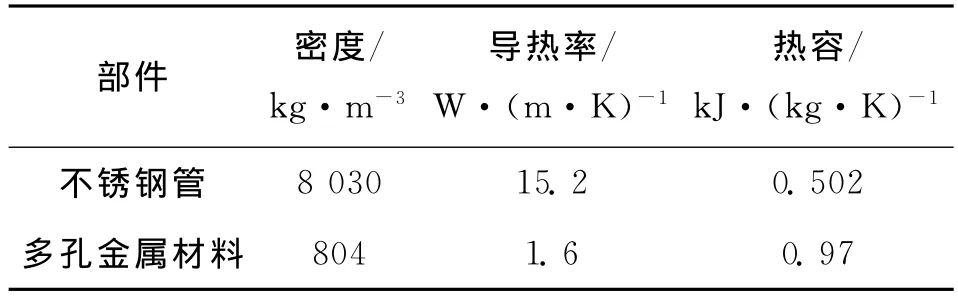
表1 高温阻抗管各部件的物性参数

重力取9.8m/s2，选择k－ε湍流模型和分离隐式求解器并进行计算。定义阻抗管中空气柱的中轴线，以及距离中轴线上、下、左、右均为16mm的4条直线的位置来对比仿真与实验的结果。仿真与实验（300℃）所得中轴线上和中轴线下的温度分布结果如图3所示。

从图3中的实验数据可以看出：管内空气在加热后产生了自然对流，温度高的气体密度小，在浮力的作用下处在较高的位置，温度较低的气体则处在较低的位置，在阻抗管中的上、下位置间存在较大的温度差，即径向温度梯度，其中材料前端面到传声器1这一段主要是轴向温度差（约为60℃），径向温度差较小。由图3可见，仿真数据与实验数据吻合较好，这为下一步仿真声场做好了准备。

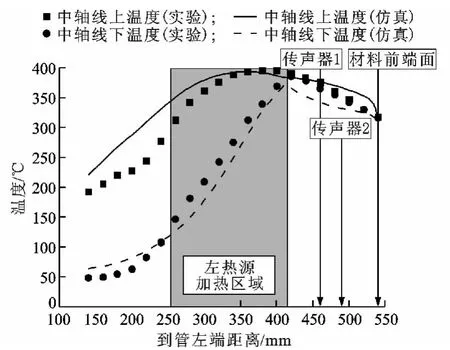
图3 温度场的仿真与实验结果对比

1.2 高温下的阻抗管声场分析

将Fluent所得到的空气温度场导入comsol软件中，计算区域为阻抗管内的圆柱空气柱。通过行波来研究声波在空气轴向温度梯度下是否满足平面波的传播特性，将2个圆柱端面设为平面波辐射边界条件，即平面波无反射，采用单频信号，入射波幅值为1Pa，管壁为硬边界条件，频率分别设为800Hz和4 800Hz，管壁为硬边界条件。仿真结果见图4、图5，图中同时画出了中轴线上、下的温度差，用来代表径向温度梯度的大小。

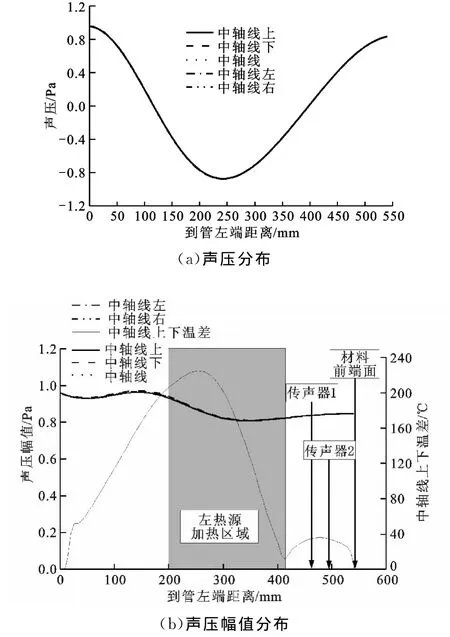
图4 入射声波频率为800Hz时的管内声场分布

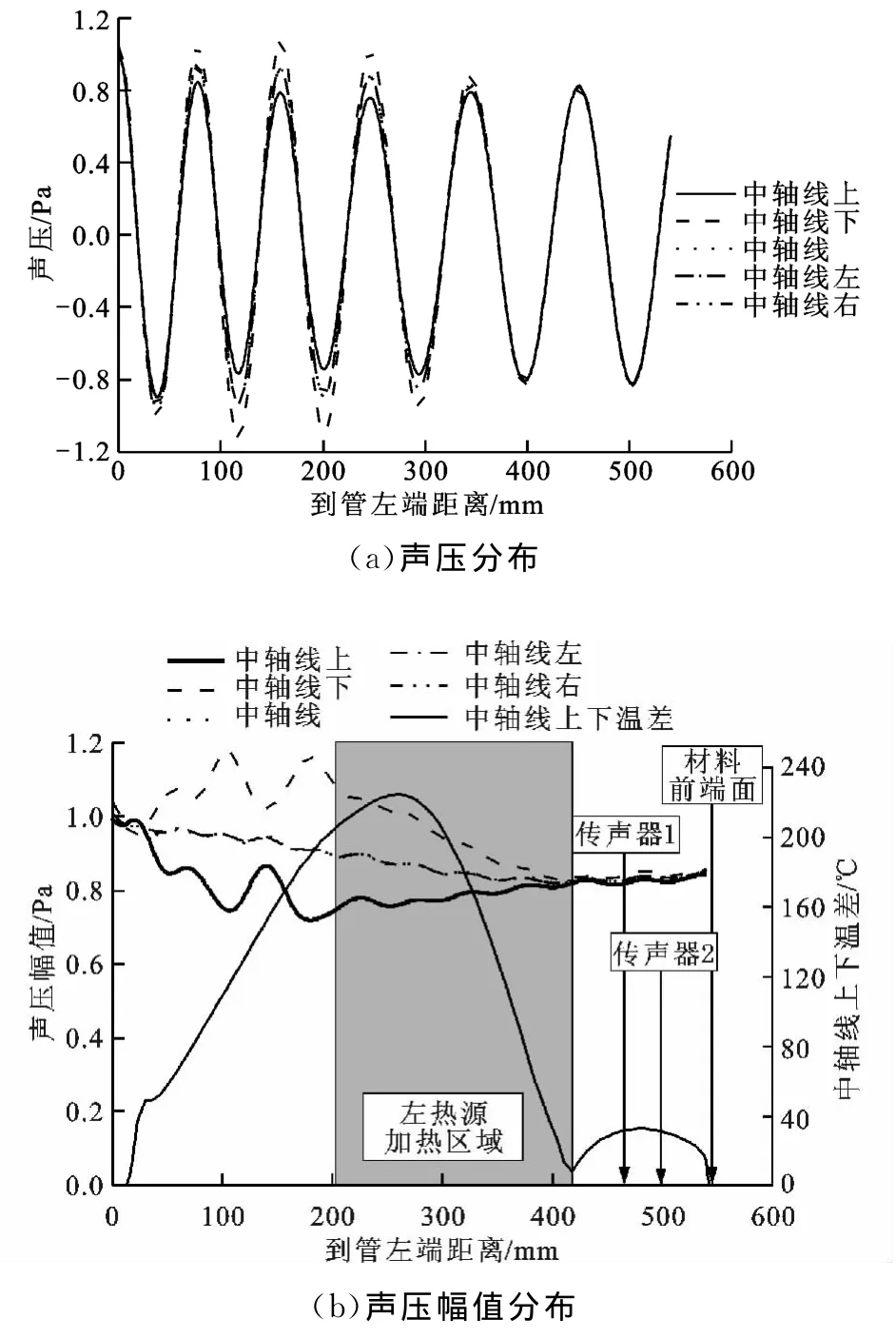
图5 入射声波频率为4 800Hz时的管内声场分布

从图4和图5可以看出：低频时温度梯度对声波的影响只体现在声压幅值的变化上，管内仍为平面波，体现了低频声波的越障性；当入射波为高频时，在径向温度梯度大的地方，如在加热区域和扬声器之间，同一截面不同位置的声压及其幅值产生了较大的变化，不再是平面波，而在径向温度梯度小的地方，如传声器附近，则产生了近似平面波。对于阻抗管中远离传声器的非平面波，可以认为是产生平面波的声源部分，故只需要考虑2个传声器处的平面波。因此，可将阻抗管内空气的均温要求扩宽到仅有轴向温度梯度。

由于实验测得材料前端空气几乎只有轴向温度梯度，因此可认为自制装置满足产生平面波的要求，能够使用传递函数法计算吸声系数。为了考虑轴向温度梯度对传递函数法的影响，需要在该梯度下对传递函数法进行修正。

2 空气有轴向温度梯度时对传递函数法的修正

2.1 修正公式推导

文献［8－10］研究了在介质的密度和声速仅沿一个方向变化时平面波的解析解。但是，文献［8］中推导解析公式时采用了均温波导管理论［11］中的处理办法，将公式（8）中的f（z）当作常项，因而得到的结果是错误的。与文献［9］相比，文献［10］给出的方法更为简单易懂——只需要通过温度场计算出密度场和声速场，然后用选定的密度和声速拟合函数进行拟合，就可以得到一个简单的解析解。密度拟合函数和声速拟合函数分别为

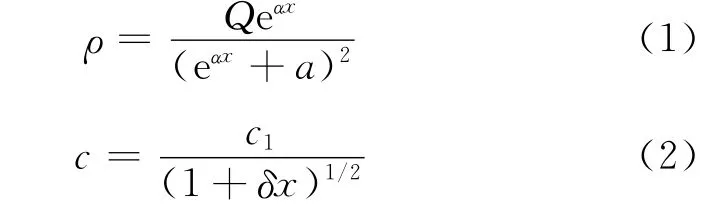
式中：Q、a、α、c1、δ均为待拟合参数。本文采用文献［10］中的方法，最终获得的空气轴向温度梯度下的平面波解析解为

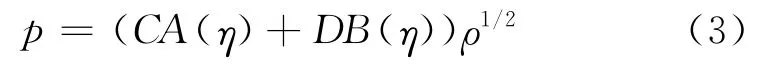
式中：A、B为艾里函数；η为位置x的函数；C、D为与温度场有关的常数。将正向波、负向波分别表示为

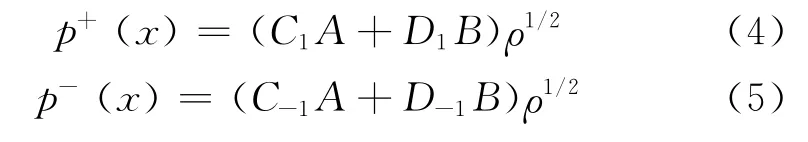
式中：C1、D1、C－1、D－1均为与温度场有关的常数。由此，可写出空气中驻波的形式为

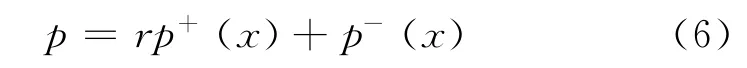
式中：r为反射系数。从传声器2处到传声器1处的传递函数为

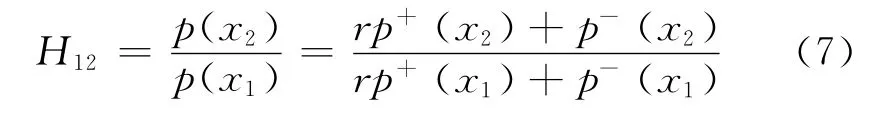
从而可求出反射系数的修正公式为

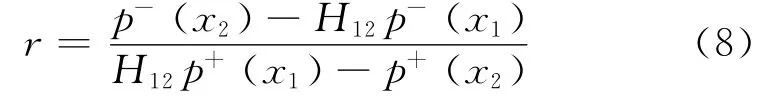
2.2 仿真验证

在comsol中分别用声强法、传递函数法以及修正传递函数法计算某多孔材料的吸声系数。声强法是通过进入材料的声强与总声强之比来计算吸声系数。利用comsol计算全场节点的声压及振速，进而计算出实际的声强，将其与入射平面波的总声强（设定值）相比可计算出吸声系数。仿真模型如图6所示。多孔材料的参数值如下：孔隙率为0.8；流阻率为10.5Pa·s/m2；黏性特征长度参数为0.49；热特征长度为470μm；黏性特征长度为240μm；曲折度为1.005 9。采用Johnson－Champoux－Allard等效流体模型计算其等效密度和等效声速。

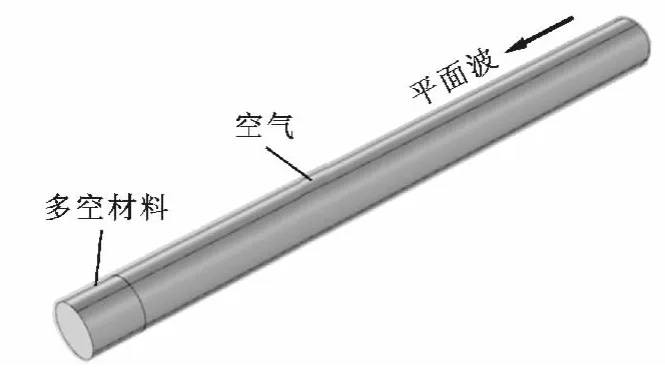
图6 声场仿真模型

空气的密度及声速用实验测得的材料前端到较远传声器之间的温度进行计算［12］，用式（1）、式（2）进行拟合可得到相应的曲线，如图7所示。

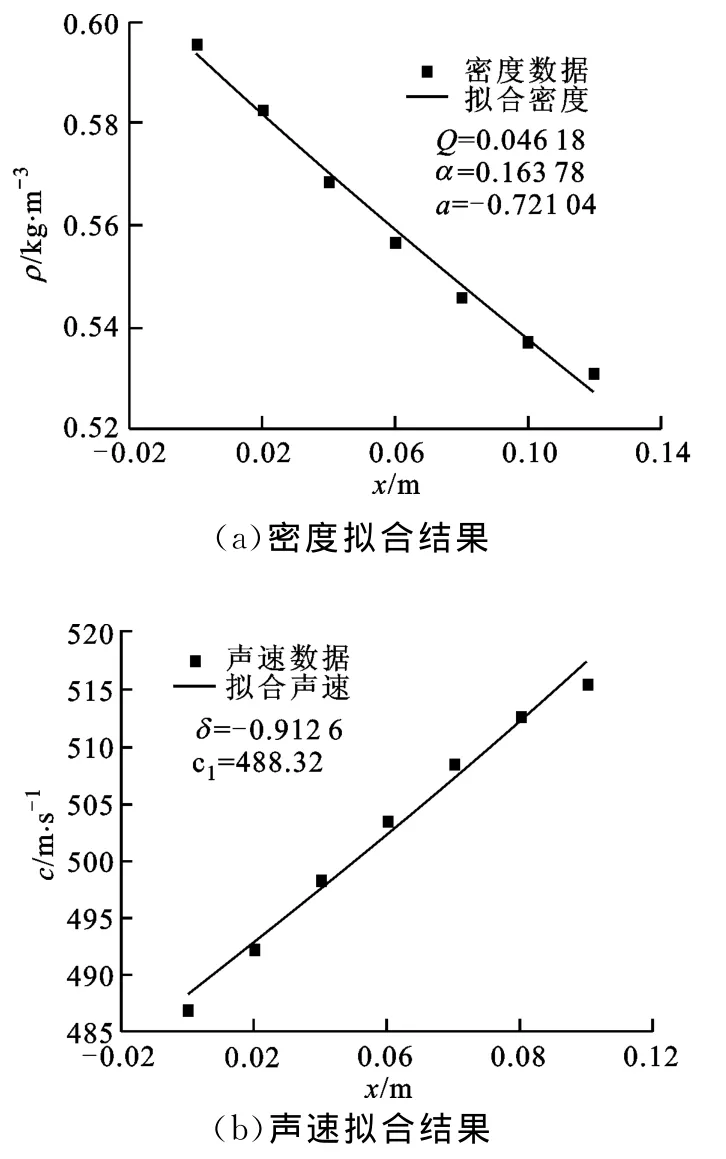
图7 密度和声速拟合结果

设多孔材料后端面及圆柱面为硬边界条件，空气柱另一端面为平面波入射，采用单频信号，幅值为1Pa。仿真结果如图8所示。

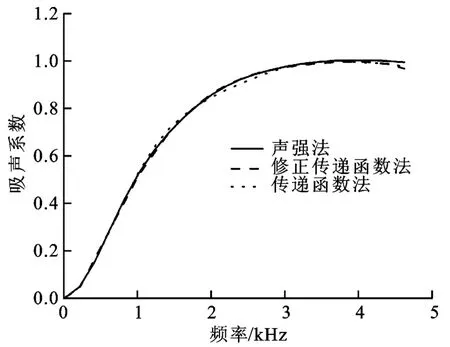
图8 吸声系数计算结果对比

从图8可知，声强法和修正传递函数法所得结果完全重合，证明了修正传递函数法的正确性。同时，修正与未修正传递函数法所得曲线的差异很小，说明材料前端空气有较小轴向温度梯度（本例为60℃/0.140m≈428.6℃/m）对吸声系数的影响不大。此结论从另一方面也说明，在设计高温阻抗管时，阻抗管前端空气有轴向温度梯度的工况是允许的，可由上述修正后的公式计算吸声系数。

3 结 论

本文对使用传递函数法时的均温要求做了推广，允许在传声器测量段空气仅有轴向温度梯度，并给出了修正公式。研究结果表明，当材料前端空气轴向温度梯度较小时，其对吸声系数计算的影响可以忽略不计。这一结论扩宽了高温阻抗管的设计空间，具有一定的潜在应用价值。

［1］卢天健，何德坪，陈常青，等.超轻多孔金属材料的多功能特性及应用 ［J］.力学进展，2006，36（4）：517－535.LU Tianjian，HE Deping，CHEN Changqing，et al.The multi－functionality of ultra－light porous metals and their applications［J］.Advances in Mechanics，2006，36（4）：517－535.

［2］彭锋，王晓林，孙艳，等.高声压级时多孔金属板的吸声特性研究 ［J］.声学学报，2009，24（3）：266－274.PENG Feng，WANG Xiaolin，SUN Yan，et al.Investigation on the sound absorption characteristics of porous metal plates at high sound pressure levels［J］.Acta Acustica，2009，24（3）：266－274.

［3］张波，陈天宁，冯凯，等.烧结金属纤维多孔材料的高温吸声性能 ［J］.西安交通大学学报，2008，42（11）：1327－1331.ZHANG Bo，CHEN Tianning，FENG Kai，et al.Sound absorption properties of sintered fibrous metals under high temperature conditions ［J］.Journal of Xi’an Jiaotong University，2008，42（11）：1327－1331.

［4］张波.多孔金属材料吸声性能研究 ［D］.西安：西安交通大学，2008：3－8.

［5］全国声学标准化技术委员会.GB/T 18696.2－2002声学阻抗管中吸声系数和声阻抗的测量：第2部分传递函数法［S］.北京：中国标准出版社，2002.

［6］冯凯.多孔金属材料高温吸声性能实验装置及吸声性能研究 ［D］.西安：西安交通大学，2008.

［7］薛昌意.变参数温度场下多孔金属材料吸声性能研究［D］.西安：西安交通大学，2010.

［8］田晓培，金韬.声波在非均匀介质波导中的传播 ［J］.复旦学报：自然科学版，2011，50（4）：527－532.TIAN Xiaopei，JIN Tao.Acoustic wave propagates in nonuniform medium waveguides［J］.Journal of Fudan University：Natural Science，2011，50（4）：527－532.

［9］SUJITH R I，WALDHERR G A，ZINN B T，An exact solution for one－dimensional acoustic fields in ducts with an axial temperature gradient ［J］.Journal of Sound and Vibration，1995，184（3）：389－402

［10］Robins A J.Reflection of a plane wave from a fluid layer with continuously varying density and sound speed［J］.Journal of the Acoustical Society of America，1991，89（4）：1686－1695.

［11］杜功焕，朱哲民，龚秀芬.声学基础 ［M］.3版.南京：南京大学出版社，2012：190－191.

［12］S A′NCHEZ－DEHESA J，ANGELOV M I，CERVERA F，et al.Sound control by temperature gradients［J］.Applied Physics Letters，2009，95：204102（1－3）.

［本刊相关文献链接］

张健，赵桂平，卢天健.泡沫金属在冲击载荷下的能量吸收特性.2013，47（11）：105－112.［doi：10.7652/xjtuxb201311019］谷伟，张虎，李增耀，等.混合气体在典型多孔介质内扩散过程的数值模拟.2012，46（3）：107－112.［doi：10.7652/xjtuxb 201203019］

张虎，谷伟，李增耀，等.氧化硅纳米多孔材料表面的水蒸气吸附动 力 学 研 究.2012，46（3）：1－8.［doi：10.7652/xjtuxb 201203001］

于雪梅.气体静压轴承用多孔SiC陶瓷的制备及静态性能.2011，45（3）：117－120.［doi：10.7652/xjtuxb201103022］

张健，赵桂平，卢天健.闭孔泡沫铝应变率效应的试验和有限元分 析.2010，44（5）：97－101.［doi：10.7652/xjtuxb201005 020］

张波，陈天宁.高声压激励下多孔金属材料的吸声性能数值计算.2010，44（3）：58－62.［doi：10.7652/xjtuxb201003012］

屈治国，徐治国，陶文铨，等.通孔金属泡沫中的空气自然对流传热 实 验 研 究.2009，43（1）：1－4.［doi：10.7652/xjtuxb 200901001］

张波，陈天宁，冯凯，等.烧结金属纤维多孔材料的高温吸声性能.2008，42（11）：1327－1331.［doi：10.7652/xjtuxb2008 11003］

张波，陈天宁.烧结金属纤维材料的吸声模型研究.2008，42（3）：328－332.［doi：10.7652/xjtuxb200803016］

DUPÈRE Iain D J，卢天健，DOWLING Ann P.声学多孔材料的孔结构优化.2007，41（11）：1251－1256.［doi：10.7652/xjtuxb200711001］

DOWLING Ann P，卢天健，DUPÈRE Iain D J.多孔泡沫材料的声 吸收 特性.2007，41（9）：1003－1011.［doi：10.7652/xjtuxb200709001］