无阀压电泵用平面锥管的非稳态特性研究

何秀华，蔡盛川，邓志丹，杨嵩，韦丹丹

（1.江苏大学能源与动力工程学院，212013，江苏镇江；2.江苏大学理学院，212013，江苏镇江；3.江苏大学流体机械工程技术研究中心，212013，江苏镇江）

压电泵的研发是集机械、电子、材料以及流体等多学科与一体的综合性研究课题，在微化学分析系统［1］、微混合器［2］、芯片冷却系统［3］、微动力系统［4］等中有着广泛的应用。无阀压电泵主要由泵体、泵盖、压电振子以及微流管等部件构成［5］。无阀压电泵中的特殊流管结构主要包括锥管、TESLA管、涡旋管、“Y”型管［6－8］等，其中锥形管结构简单、易于加工，对其性能和结构进行优化是提高无阀压电泵性能的重要途径之一。

以往关于无阀压电泵用流管的研究多是在稳态流动情况下进行的，而实际上压电泵内流动情况是非稳态的。Sun等对锥管内的非稳态流动进行了数值模拟研究，分析了扩散角和驱动频率对其流动性能的影响［9］。Ahmadian等建立了二维锥管模型，研究了其在不同频率下的动态特性［10］。Wang等通过数值模拟研究锥管的稳态与非稳态特性，发现非稳态情况下St取0.013时可获得最大净流量［11］。Tanaka等对锥管无阀压电泵进行了实验研究，结果显示流量随驱动频率的增大而增大［12］。Nabavi等在高频（10kHz≤f≤30kHz）下对不同锥角的平面锥管进行了数值模拟研究，发现当驱动频率很高时，速度变化相对于压强变化滞后的相位约为π/2［13］。

以上文献多在固定压力幅值下研究高频率范围内锥管的非稳态特性，而在不同压力幅值下低频率范围内对平面锥管非稳态特性的研究较为缺乏，且锥管内的非稳态流动易发生分离，产生的旋涡对其性能有重要影响。由于非稳态旋涡运动规律复杂，目前该方面的研究极为有限。因此，本文应用数值模拟的方法，研究了不同压力幅值下低频率范围内平面锥管的流动特性，探究旋涡的运动规律及其对锥管输出特性的影响。

1 无阀压电泵用锥管的理论分析

锥管无阀压电泵的工作原理如图1所示。无阀压电泵利用流管两个方向流动阻力不同的特性，导致在压电振子振动的一个周期里通过流管的流量不相等，从而实现流体单向泵送。

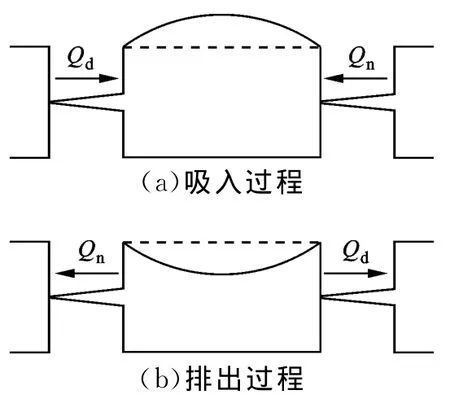
图1 无阀压电泵的工作原理

设流体沿锥管扩散方向的流动为正向流动，沿收缩方向的流动为反向流动，则一个周期内流体沿正（反）方向流动时，所受压力为［9］

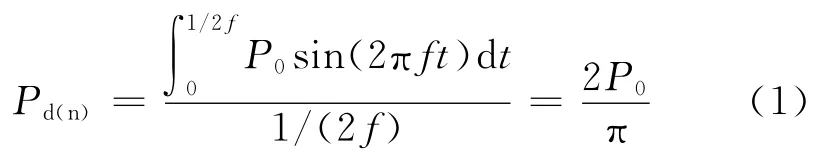
式中：f为驱动频率；P0为压力幅值；t为时间。

流体在锥管内沿正（反）方向流动时的压力损失系数为

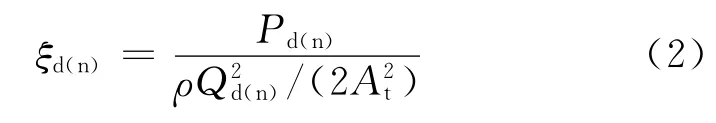
式中：ρ为流体密度；At为锥管最小过流断面面积；Qd（n）为一个周期内锥管正（反）方向的体积流量。

一个周期T内通过平面锥管的净流量为

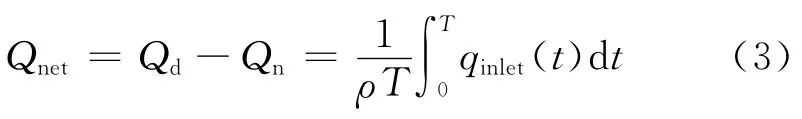
式中：qinlet为通过锥管进口的瞬时质量流量。无阀压电泵的整流效率为［14］

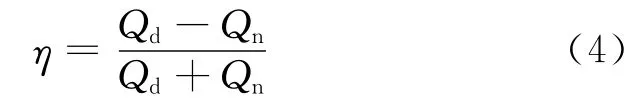
η的大小反映了微泵效率的高低，其他条件相同时，η越大，无阀压电微泵的效率越高。

2 数值计算

2.1 计算模型

应用于无阀压电泵中常见的锥管结构有3种，分别为圆锥管、棱锥管以及平面锥管。通过实验［15］发现在最佳输出状态下，平面锥管的长度比圆锥管短10%～80%，有利于压电泵的微型化。本文研究的平面锥管结构如图2所示，包括进口缓冲腔、锥管段及出口缓冲腔。影响平面锥管流阻性能的主要结构参数为锥管最小过流断面宽度w，扩散管长度L，锥角θ及锥管高度h。本模拟中平面锥管进口倒圆角，其圆角半径R取0.075mm，w取150μm，h取150μm，L取3mm，θ取5°和10°。

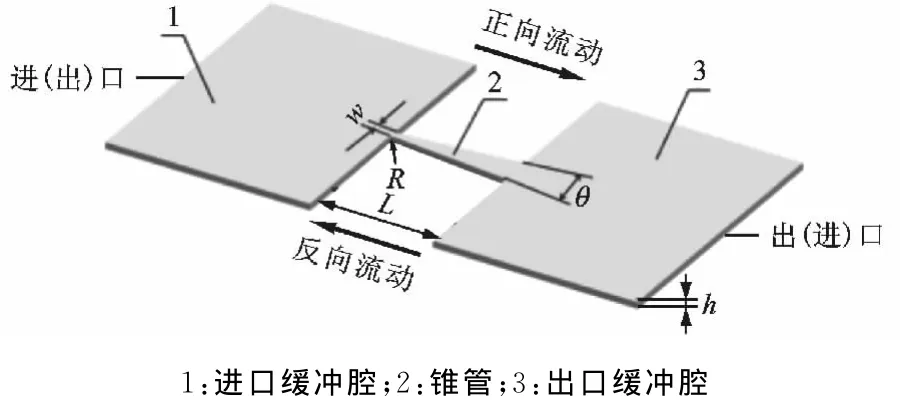
图2 平面锥管结构

2.2 初始和边界条件设定

利用CFX对θ为5°和10°的锥管内的流动进行数值模拟，流动介质选用不可压缩的水，密度ρ为1 000kg/m3，运动黏度ν为1×10－6m2/s，温度为20℃，忽略流体重力及锥管内气泡混入所产生的影响。

锥管段采用结构网格进行划分，进（出）口缓冲腔区域采用非结构网格进行划分，由于锥管段与进（出）口缓冲腔衔接处压力梯度较大，需要对这些区域的网格加密。平面锥管进口施加随时间按正弦规律变化的压力边界条件，Pinlet＝P0sin（2πft），P0取0.5、1、5kPa，锥管出口相对压力设为0。

当 Womersley数Wo（Wo＝（Dh/2）（f/ν）1/2，其中Dh为锥管最小截面处的水力直径）超过45时，振荡流为湍流［16］，本模拟中Dh为150μm，f取最大值500Hz时，计算可得Wo为1.677，远小于45。另外，根据层流向湍流过渡的经验公式Ret＝30L/Dh［17］得到Ret为600，而模拟结果表明最大雷诺数约为485，所以采用层流对平面锥管进行非稳态模拟。当驱动频率较低（Wo＜1.06）时，经过约半个周期的计算，流量开始呈现出稳定的周期性变化；当驱动频率较高（Wo＞1.06）时，要使流量变化趋于稳定则需要更多的迭代周期（当f＝500Hz时，需要约两个周期）。因此，在较低频率下计算两个压力周期且计算数据从第2个周期开始取值，较高频率下计算数据从第3个压力周期开始取值。

2.3 网格无关性分析

图3a为P0＝0.5kPa、θ＝5°、f＝10Hz、网格数分别约为40万和80万时前两个周期内通过平面锥管的瞬时流量随时间的变化关系，可以看出两条曲线基本相同，瞬时流量的最大相对误差为3.2%，净流量的最大相对误差为1.8%。为节省计算资源，根据锥管角度的不同选取网格数为40万～50万。图3b为P0＝0.5kPa、θ＝5°、f＝10Hz，一个周期内时间步为100和200时前两个周期内通过平面锥管的瞬时流量随时间的变化关系，结果显示时间步对瞬时流量的影响很小，瞬时流量的最大相对误差仅为0.92%。

3 计算结果

3.1 滞后效应分析

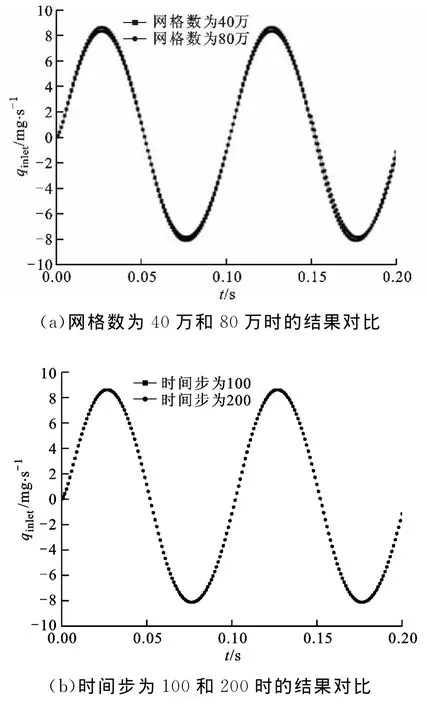
图3 不同网格数和时间步下锥管进口流量随时间的变化曲线（P0＝0.5kPa，θ＝5°，f＝10Hz）

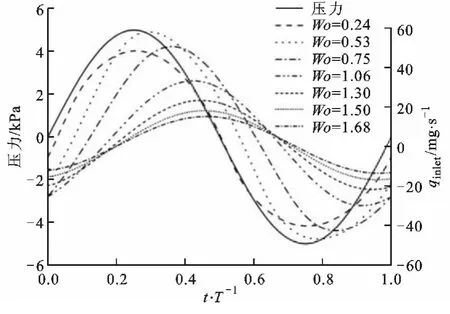
图4 不同Wo下平面锥管进口流量随时间的变化曲线（P0＝5kPa，θ＝5°）

图4为P0＝5kPa、θ＝5°、不同Wo下平面锥管进口流量随时间的变化曲线。结果表明，速度变化相对于压力变化存在滞后性，两者之间的相位差随着Wo的增大而增大。非稳态流动情况下平面锥管内的流体质点受压力、黏性力和惯性力的共同作用。当Wo很小（Wo＝0.24）时，驱动频率很低，管内流速较高，非稳态惯性力所占比重较小，使得流量与压力变化几乎同步；随着Wo的增大，驱动频率升高，管内流速降低，非稳态惯性力对流动的影响逐渐加强，使得流量变化相对于压力变化的滞后增大。由图5可以看到，相同Wo下，压力幅值越大，管内流速越大，流量相对于压力的滞后越小。

图5 不同压力幅值下平面锥管进口流量随时间的变化曲线（Wo＝0.75，θ＝5°）

3.2 最大流量分析

不同压力幅值和锥角下平面锥管正（反）方向的Remax（Remax＝（umaxDh）/ν，其中umax表示平面锥管最小过流断面处速度的最大值）与Wo的变化关系如图6所示，最大Remax处，流量取得最大值。非稳态流动情况下，流量相对于压力的滞后效应造成锥管最大流量的降低，速度剖面（速度剖面指的是平面锥管过流断面在同一时刻的速度值所形成的曲面）相对于速度变化的滞后效应造成锥管最大流量的提高［18］。由文献［19］可知，扩散角、流速越大，速度剖面相对于速度变化的滞后越容易产生。

当P0＝0.5kPa时，对θ为5°的锥管，其Remax随Wo的增大而减小，这是由于小角度锥管内流速较小且分布较为平均，速度剖面相对于速度变化的滞后较小，且在较低压力幅值下流量相对于压力的滞后较大。对于θ为10°的锥管，当Wo＜0.53时，Remax随Wo的增大而增大，表明速度剖面相对于速度变化的滞后效应对Remax的影响大于流量相对于压力的滞后效应的影响；当Wo＞0.53时，Remax随Wo的增大而减小，表明后者的影响大于前者。当P0＝1kPa时，两种角度锥管的Remax随Wo的增大而减小，表明速度剖面相对于速度变化的滞后效应对Remax产生的影响小于流量相对于压力的滞后效应的影响。当P0＝5kPa时，对θ为5°的锥管，当Wo＜0.53时，Remax随着Wo的增大而增大，当Wo＞0.53后，Remax随Wo的增大而减小；对于θ为10°的锥管，其正向流动的Remax随Wo的变化与θ为5°的锥管具有相同的趋势，而反向流动的Remax随Wo的增大而减小。

3.3 净流量

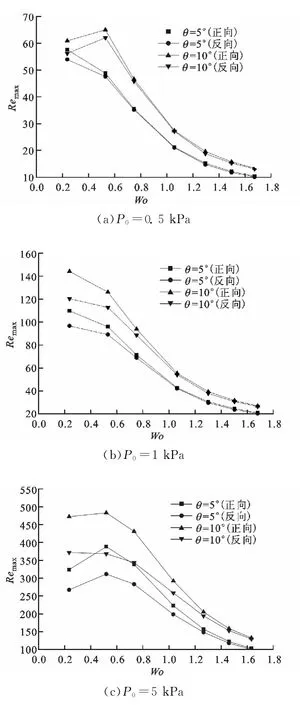
图6 不同压力幅值和锥角下Remax随Wo的变化曲线

图7为不同P0和θ下通过平面锥管的净流量Qnet随Wo的变化。较低压力（P0＝0.5，1kPa）下，当Wo＜0.53时，Qnet随Wo的增大以较快的速率递减，之后缓慢减小，当Wo＞1.06后，Qnet随Wo的增大有小幅的递增；较高压力幅值（P0＝5kPa）下，如图7c所示，Qnet随Wo的增大而减小，同样在Wo较小时递减速率较快，当Wo＞1.30后，Qnet基本不随Wo的增大而变化。同时可以看出，P0和θ越大，Qnet也越大，且随Wo的增大，锥角对Qnet的影响作用减弱。

3.4 压力损失系数

根据式（1）、（2）分别计算出ξd、ξn，得到其随Wo的变化如图8所示。ξd始终小于ξn，使得一个周期内获得沿正方向的净流量，且ξd和ξn均随Wo的增大而增大，随P0的增大而减小；同时可以看出，ξd和ξn随θ的增大而减小，且当Wo＞1.06后，锥角对ξd和ξn的影响越来越明显。

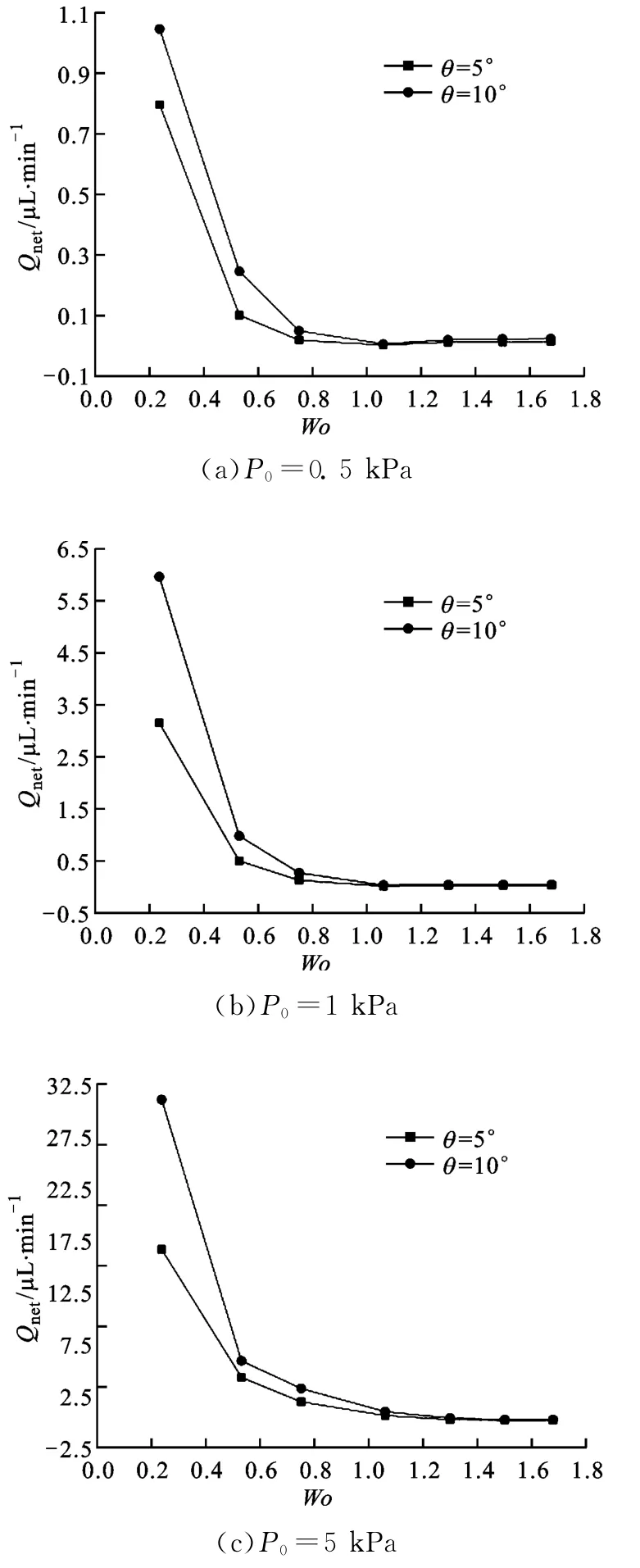
图7 不同压力幅值和锥角下净流量随Wo的变化曲线

3.5 整流效率

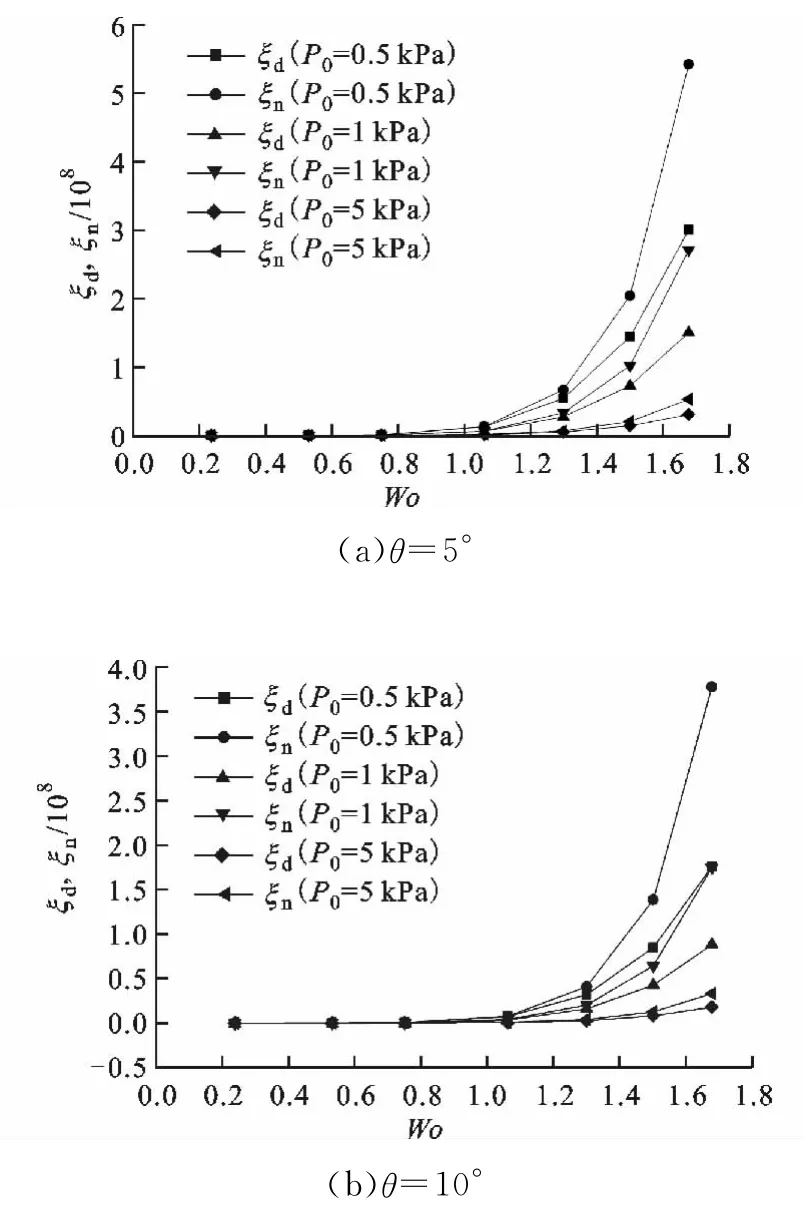
图8 不同压力幅值和锥角下ξd、ξn随Wo的变化曲线

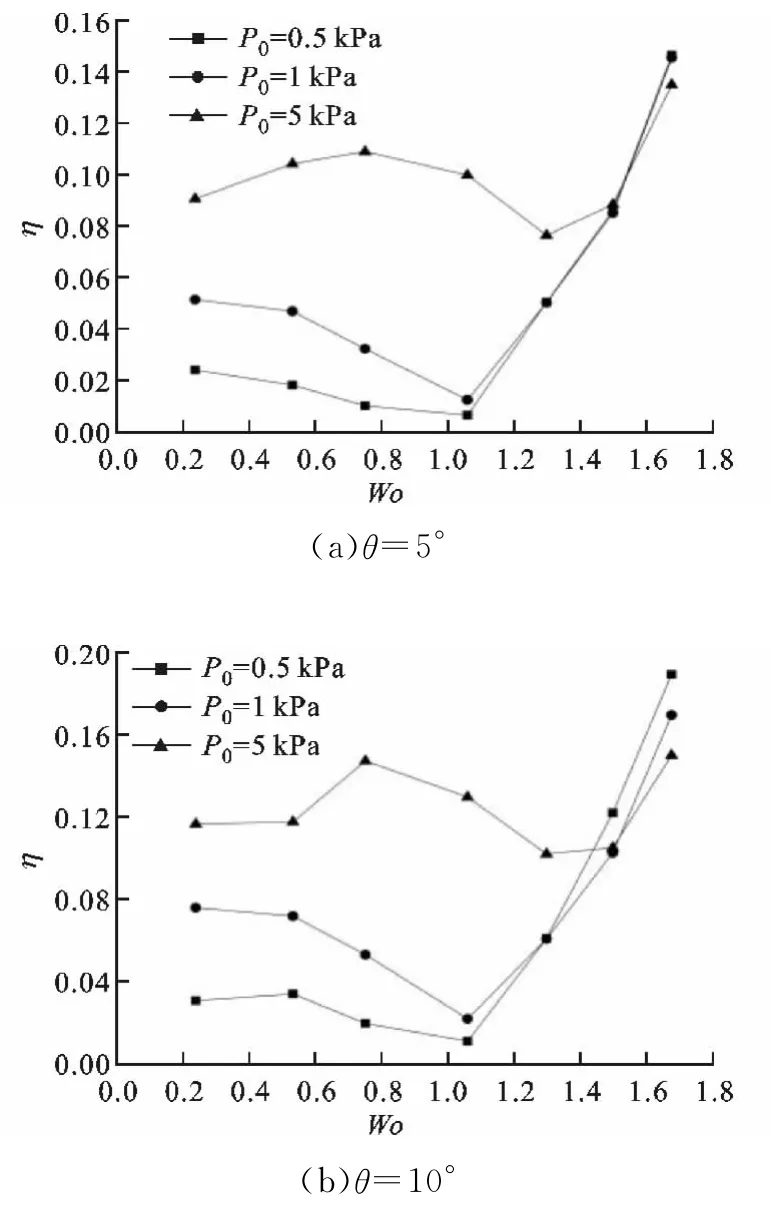
图9 不同压力幅值和锥角下η随Wo的变化曲线

微泵效率η随Wo的变化如图9所示。不同角度的平面锥管，在不同压力幅值下η随Wo的变化具有相同的趋势；当P0为0.5和1kPa、Wo＜1.06时，η均随Wo的增大而减小，在Wo＝1.06处取得最小值，当Wo＞1.06后，η随Wo的增大而显著增大；P0为5kPa时，η均先随Wo的增大而增大，之后随着Wo的增大而减小，在Wo＝1.3处取得最小值，并且当Wo＞1.5后显著增大。同时结果表明，当Wo＜1.3时，P0越大，η也越大，当Wo＞1.3后，P0为0.5、1和5kPa对应的η均随Wo的增大而增大，但增幅依次变大，致使当Wo＝1.68时表现出P0越小，η越高；对θ为10°的微泵，在P0为0.5kPa时η达到了18.9%。

3.6 平面锥管内部流场分析

非稳态流动情况下平面锥管内产生的旋涡运动增加了流管流阻。图10为P0＝1kPa、θ＝10°、Wo＝0.75时锥管中间截面在一个周期内不同时刻的速度矢量图。正向流动时，靠锥管面积较大一端的壁面上产生一对旋涡，随着锥管两端压差的减小，该旋涡脱离壁面向锥管中心移动且大小不断变化；反向流动时，靠锥管面积较小一端的壁面上产生一对旋涡，同样随着锥管两端压差的减小，该旋涡脱离壁面向锥管中心移动且大小不断变化。

图10 平面锥管中间截面的速度分布

图11为P0＝0.5kPa、θ＝5°时锥管段内旋涡的持续时间随Wo的变化，由图可知反向流动时旋涡的持续时间始终大于正向流动时的持续时间。Wo较小时，旋涡的持续时间较短，由此造成的压力损失较小，故通过锥管的净流量较大，随着Wo的增大，旋涡的持续时间增大，由旋涡运动造成的压力损失增大，使得通过锥管的净流量减小，当Wo＞1.06后，正向压力损失随Wo的增大而减小，反向压力损失却随Wo的增大而增大，从而有如图7a所示流量有小幅递增的现象。随着压力幅值进一步增大，正（反）方向旋涡的持续时间出现相反变化，对应的Wo变大，当P0＝5kPa时，给定Wo范围内正（反）方向旋涡的持续时间均随Wo的增大而增大，因而通过锥管的净流量随Wo的增大而减小。

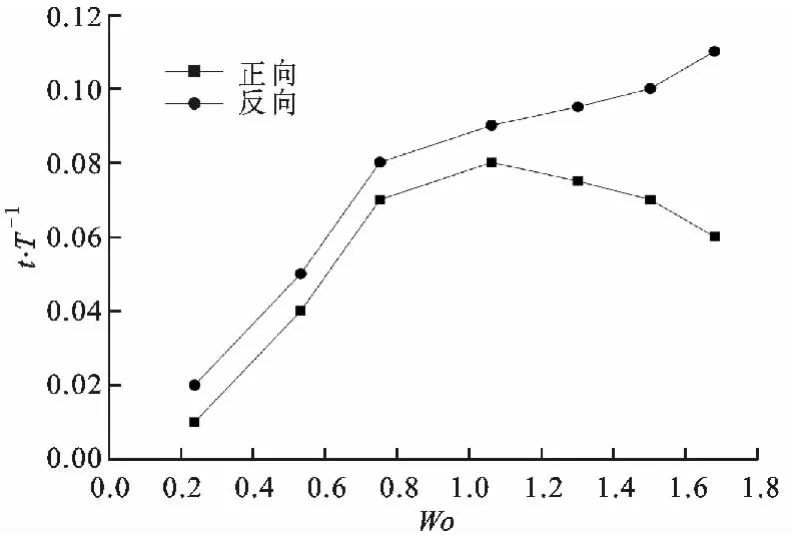
图11 锥管中旋涡的持续时间随Wo的变化曲线

4 结 论

（1）流量变化滞后于压力变化，且Wo越大，压力幅值越小，相位差越大。

（2）P0为0.5kPa时，θ为5°的锥管Remax随Wo的增大而减小，θ为10°的锥管Remax随Wo的增大先增大后减小；P0为1kPa时，两种锥管的Remax随Wo的增大而减小；P0为5kPa时，θ为5°的锥管Remax存在最大值，θ为10°的锥管正向流动时Remax随Wo的变化与θ为5°的锥管具有相同的趋势，而反向流动时Remax随Wo的增大而减小。

（3）较低压力幅值（P0为0.5、1kPa）下，净流量先随Wo的增大而减小，之后有小幅递增；较高压力幅值（P0为5kPa）下，净流量随Wo的增大而减小；P0和θ越大，通过平面锥管的净流量也越大。

（4）平面锥管正（反）方向的压力损失系数ξd、ξn均随Wo的增大而增大，随P0和θ的增大而减小，且ξd始终小于ξn。微泵的整流效率η随Wo变化有相同的趋势，较低Wo下，P0越大，η也越大，较高Wo下，P0越小，η越大；θ为10°的微泵，当P0为0.5kPa、Wo为1.68时η达到了18.9%。

（5）非稳态流动情况下平面锥管内产生的旋涡运动增加了流动阻力，且旋涡运动的持续时间越长，通过锥管的净流量越小。

［1］WEIBEL D B，WHITESIDES G M.Applications of microfluidics in chemical biology［J］.Current Opinion in Chemical Biology，2006，10（6）：584－591.

［2］SHEEN H J，HSU C J，WU T H，et al.Experimental study of flow characteristics and mixing performance in a PZT self－pumping micromixer［J］.Sensors and Actuators：A Physical，2007，139（2）：237－244.

［3］GARIMELLA S，SINGHAL V，LIU D.On－chip thermal management with microchannel heat sinks and integrated micropumps ［J］.Proceedings of the IEEE，2006，94（8）：1534－1548.

［4］SINGHAL V，GARIMELLA S V，RAMAN A.Microscale pumping technologies for microchannel cooling systems［J］.Applied Mechanics Reviews，2004，57（3）：191－221.

［5］邓志丹，何秀华，杨嵩，等.无阀压电泵用椭圆组合管正交优化设计与实验 ［J］.农业机械学报，2013，44（9）：284－289.DENG Zhidan，HE Xiuhua，YANG Song，et al.Orthogonal optimization design and experimental of oval composite tube in valveless piezoelectric pump ［J］.Transactions of the Chinese Society of Agricultural Machinery，2013，44（9）：284－289.

［6］FORSTER F K，BARDELL L，AFROMOWITZ M A，et al.Design，fabrication and testing of fixed－valve micro－pumps［C］∥Proceedings of the ASME Fluids Engineering Division.New York，USA：ASME，1995：39－44.

［7］IZZO I，ACCOTO D，MENCIASSI A，et al.Modeling and experimental validation of a piezoelectric micropump with novel no－moving part valves［J］.Sensors and Actuators：A Physical，2007，133（1）：128－140.

［8］张建辉，黎毅力，夏齐霄，等.“Y”形流管无阀压电泵振动分析及泵流量计算 ［J］.光学精密工程，2007，15（6）：922－929.ZHANG Jianhui，LI Yili，XIA Qixiao，et al.Research on vibration and pump flow rate of valveless piezoelectric pump with Y－shape tubes［J］.Optics and Precision Engineering，2007，15（6）：922－929.

［9］SUN C L，HUANG K H.Numerical characterization of the flow rectification of dynamic microdiffusers［J］.Journal of Micromechanics and Microengineering，2006，16（7）：1331－1339.

［10］AHMADIAN M T，SAIDI M H，MEHRABIAN A，et al.Performance of valveless diffuser micropumps under harmonic piezoelectric actuation［C］∥Proceedings of the 8th Biennial ASME Conference on Engineering Systems Design and Analysis.New York，USA：ASME，2006：693－699.

［11］WANG C T，LEU T S，SUN J M.Unsteady analysis of microvalves with no moving parts［J］.Journal of Mechanics，2007，23（1）：9－14.

［12］TANAKA S，TSUKAMOTO H，MIYAZAKI K.Development of diffuser/nozzle based valveless micropump［J］.Journal of Fluid Science and Technology，2008，3（8）：999－1007.

［13］NABAVI M，MONGEAU L.Numerical analysis of high frequency pulsating flows through a diffusernozzle element in valveless acoustic micropumps［J］.Microfluidics and Nanofluidics，2009，7（5）：669－681.

［14］SINGHAL V，GARIMELLA S，MURTHY J.Low Reynolds number flow through nozzle－diffuser elements in valveless micropumps［J］.Sensors and Actuators：A Physical，2004，113（2）：226－235.

［15］OLSSON A，STEMME G，STEMME E.Numerical and experimental studies of flat－walled diffuser elements for valve－less micropumps［J］.Sensors and Actuators：A Physical，2000，84（1/2）：165－175.

［16］FRANK M W.Viscous fluid flow ［M］.New York，USA：McGraw－Hill Higher Education，1991：135－136.

［17］GRAVESEN P，BRANEBJERG J，JENSEN O S.Microfluidics：a review ［J］.Journal of Micromechanics and Microengineering，1993，3（4）：168－182

［18］曹超，应济，焦致凯.无阀微泵非稳态特性及整流效率仿真 ［J］.浙江大学学报：工学版，2013，47（6）：1036－1042.CAO Chao，YING Ji，JIAO Zhikai.Simulation of unsteady characteristics and rectification efficiency of valveless micropump［J］.Journal of Zhejiang University：Engineering Science，2013，47（6）：1036－1042.

［19］SCHLICHTING H，GERSTEN K.Boundary－layer theory ［M］.Bochum，Germany：Springer，2000：731－750.