某自行火炮全弹道多学科优化设计

牛福强，洪亚军，徐 诚

（1.陆军军官学院，合肥 230031；2.南京理工大学机械工程学院，南京 210094）

某自行火炮全弹道多学科优化设计

牛福强1，2，洪亚军2，徐 诚2

（1.陆军军官学院，合肥 230031；2.南京理工大学机械工程学院，南京 210094）

为提高某自行火炮弹丸的杀伤效能，寻求该火炮全弹道设计参数间更优的匹配关系，并缩短全弹道设计周期，根据其包含的内弹道、外弹道和终点效应3个分学科之间的耦合关系，建立自行火炮全弹道多学科优化设计模型。以射程最大、杀伤面积最大为优化目标，进行全弹道优化设计。与单目标优化方法对比，多目标优化有效提高了该火炮弹道的综合性能，避免了单个目标优化时其他目标劣化的现象。

自行火炮，优化设计，全弹道，多学科优化

引言

采用传统方法对身管武器弹道进行优化设计时，通常对内弹道、外弹道和终点弹道3个弹道过程分别进行优化。该优化设计方法忽略了各弹道过程之间的耦合关系，在某弹道过程达到最优时，其余弹道过程有可能并不能满足设计要求。在确定最终设计方案时，往往只能依靠经验来选择和调整，选取一个各弹道过程均能满足的相对较优解，很难达到全弹道过程的最优；此外，在优化设计时，当某个弹道过程不能满足设计要求时，需要对其他弹道过程重新进行优化，优化效率较低。本文将各分学科模型集成为一个多目标多学科优化设计模型，实现各分学科仿真模型之间数据的相互自动传递。

1 各学科仿真模型及耦合关系

1.1 内弹道仿真模型

由于内弹道过程比较复杂，为更好地对内弹道过程进行研究，做如下假设：

（1）t=0时刻，所有火药同时着火；

（2）火药燃烧遵循几何燃烧定律；

（3）弹带与炮膛形成了一个完全的气体密封系统；

（4）火药气体的流动是零维的、无黏性的和不可压缩的。

建立内弹道计算模型

（1）形状函数

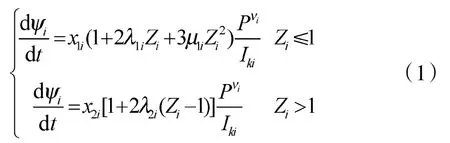
（2）燃速方程

（3）弹丸运动方程

（4）弹丸运动方程

（5）内弹道基本方程

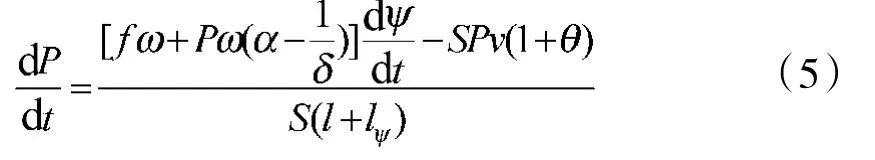
式中：

式中：x、λ、μ为火药形状特征量；Z为火药已燃相对厚度；ψ为火药已燃百分数；P为平均压力；φ为次要功计算系数；m为弹丸质量；v为弹丸运动速度；t弹丸运动时间；S枪膛断面积；l为弹丸行程长；lψ为药室自由容积缩径长；f为火药力；ω为装药质量；θ为火药热力参数；Δ为火药装填密度。

1.2 外弹道仿真模型

建立包括身管火炮弹丸自转在内的质点外弹道方程如下所示。根据弹丸出膛口时的初速，根据外弹道方程编制程序迭代求解出火炮射击时的射角、弹道最大高度、弹丸飞行时间等。

式中：t为弹丸飞行的时间，c为平均弹道系数；H（y）为气重函数；G（v）为阻力函数；x，y为弹丸在飞行中t时刻的坐标；v为弹丸飞行速度；vx、vy为弹丸在x，y方向的分速度；Jζ为弹丸对转轴的极转动惯量；γ.为弹丸自转角速度；N为弹丸自转转数。

1.3 终点弹道仿真模型

设弹丸在目标区域爆炸，破片向四周飞散，其中部分破片击中地面上的目标并致其伤亡。

弹丸破片在目标位置（x，y）的杀伤概率取决于破片的杀伤概率、破片的分布以及目标的暴露面积，其杀伤概率数学模型为：

榴弹杀伤面积表示弹丸爆炸时破片对地面目标能够产生有效杀伤的面积，榴弹杀伤面积可表示为：

1.4 各学科耦合关系

全弹道包括内弹道、外弹道和终点弹道3个学科，它们之间相互有着耦合关系，如图1所示。

图1 各学科耦合关系

内弹道的输出参数V0，为外弹道计算的输入参数；外弹道输出参数落速Vc与落角Tc，是终点弹道的输入参数；终点弹道计算出的弹丸形状参数与炸药质量，决定着弹丸的质量，弹丸的质量又是内弹道与外弹道的输入参数，直接影响着内、外弹道的计算结果。

2 集成优化设计模型

以弹丸结构参数、内弹道装药诸元、射击条件等为设计参数，以最大膛压、火药能量利用效率、火药燃烧相对结束位置、装药密度为约束条件，以其杀伤面积与射程最大为优化目标，建立身管火炮全弹道多学科优化设计模型。

2.1 目标函数

对于火炮来讲，杀伤面积与射程是重要的战术技术指标，也是设计人员追求的设计指标，本模型以杀伤面积与火炮射程为目标函数。

杀伤面积

火炮射程

以理论最大射程的45°发射角为例，以杀伤面积和火炮射程最大为优化目标，权重都为0.5，进行仿真优化。

2.2 设计变量

设计变量是用于描述火炮优化设计中可被设计者控制的一组相对独立的变量，用于身管火炮优化设计的设计变量包括内弹道、外弹道及终点弹道3个模型的40个变量：

表1 变量

表1中：r0、r1、r2、r3、h1、h2、h3为从弹头至弹尾的内3段尺寸R0，R1，R2，R3，H1，H2，H3为从弹头至弹尾的外3段尺寸。

2.3 约束条件

约束条件为在身管火炮优化设计过程中必须要满足的条件，本算例中约束条件一共设了4个。

式中：ηω为火药能量利用效率，ηk为火药燃烧相对位置，Δ为装药密度，Pm为最大膛压。

2.4 优化设计流程

全弹道优化设计模型工作流程如图2所示：

图2 全弹道优化设计流程图

3 优化结果

以弹丸杀伤面积与最大射程为优化目标，应用模拟退火优化算法，对该模型进行优化求解，经过3 480次迭代达到收敛。通过优化，获得了火炮弹丸杀伤效能达到最优时弹丸结构、内弹道装药及射击条件等各参数。与原设计相比，杀伤面积收敛过程如图3所示，杀伤面积由1 055.53 m2提升到1 250.26 m2，提高了18.45%；最大射程收敛过程如图3所示，最大射程由14 634.19提升到15 995.08，提高了9.3%。

图3 杀伤面积优化结果曲线图

图4 射程优化结果曲线图

优化前后各参数如表2所示。

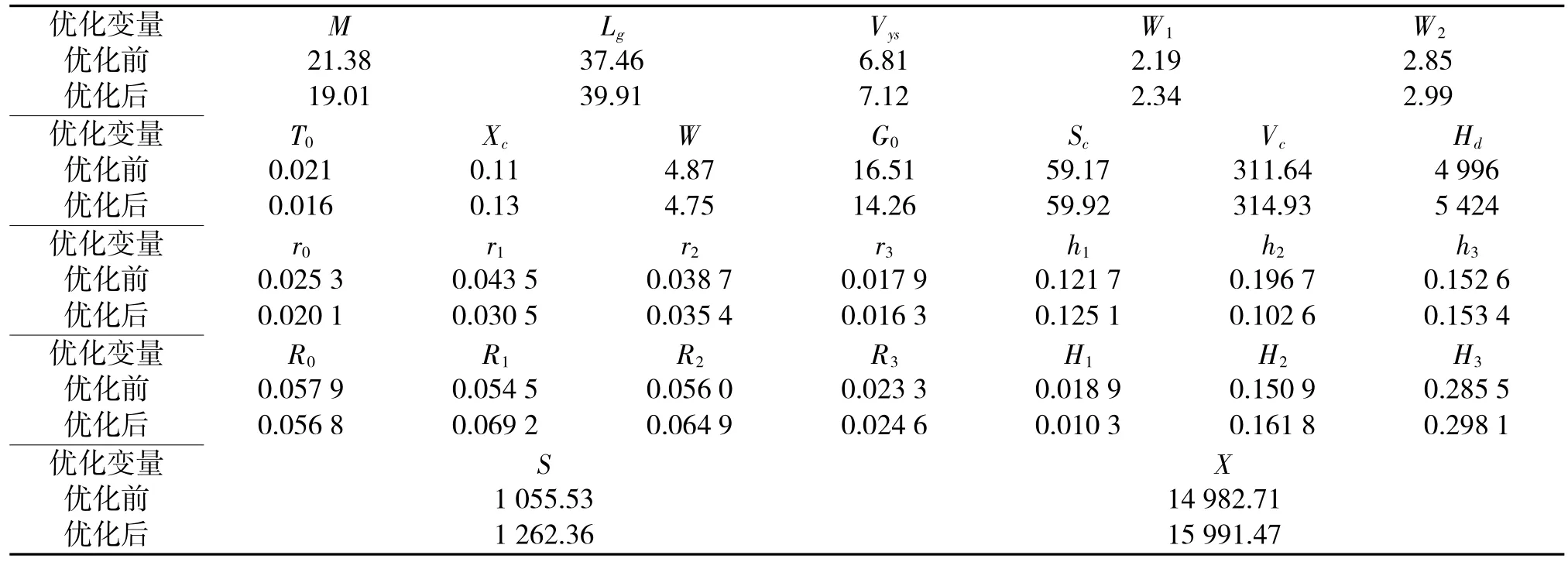
表2 优化前后各弹道参数对比

4 结束语

本文以某型自行火炮为研究对象，考虑其全弹道涉及的多个领域模型间的耦合关系，建立多学科优化设计模型，并对其进行多目标优化设计。通过多学科多目标优化设计，实现各个所涉及到的学科间的有机协调，获得了整体最优时的优化设计方案，与原设计方案相比，优化后火炮弹道性能得到显著提高。本文为火炮弹道设计提供了一种可行新方法，对自行火炮武器系统的设计具有指导意义。

［1］钱林方.火炮弹道学［M］.北京：北京理工大学出版社，2009.

［2］王振国，陈小前，罗文彩，等.飞行器多学科优化设计理论与应用研究［M］.北京：国防工业出版社，2006.

［3］洪亚军，王亚平，徐 诚.单兵榴弹武器系统集成优化设计方法［J］.南京理工大学学报，2012，36（（2）：216-220.

［4］李克婧，张小兵.火炮全弹道过程仿真及应用［J］.火炮发射与控制学报，2010，32（6）：48-52.

［5］毛保全，邵 毅.火炮自动武器优化设计［M］.北京：国防工业出版社，2007.

Research of Multidisciplinary Design Optimization to a Self-propelled Gun's Full Ballistics

NIU Fu-qiang1，2，HONG Ya-jun2，XU Cheng2
（1.Army officer Academy of PLA，Hefei 230031，China；
2.School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing210094，China）

To improve a self-propelled guns kill efficiency of the projectile，and find the design parameters of optimal matching relations，and shorten the design cycle，the model of self-propelled gun's full ballistic multidisciplinary design optimization is build，which depends on the coupling relationship of interior ballistic，exterior ballistics，and the terminal ballistic.To get the maximum of lethal area and range of fire，the full ballistics is optimized.Compared with the traditional design methods which are single subject optimization，the multidisciplinary design optimization method can effectively improve the comprehensive performance of the gun'ballistic，and avoid the phenomenon of other target's degradation when a single target optimization.

self-propelled gun，optimaldesign，the whole trajectory，multidisciplinary design optimization

TN971

A

1002-0640（2014）11-0160-04

2013-08-05

2013-11-10

牛福强（1977- ），男，河南武陟人，博士。研究方向：自行火炮总体设计优化。