基于Matlab/Simulink的无人机自主着陆过程仿真*
2014-06-15陈晓飞董彦非
陈晓飞,董彦非
(南昌航空大学飞行器工程学院,南昌 330063)
基于Matlab/Simulink的无人机自主着陆过程仿真*
陈晓飞,董彦非
(南昌航空大学飞行器工程学院,南昌 330063)
为了研究无人机自主着陆过程中高度、速度和飞行轨迹角的变化特性,以提高无人机自主着陆的安全性和精确性,需要对无人机着陆过程进行数学建模。采用模块化设计思想,根据无人机非线性动力学和运动学方程,在Matlab/Simulink环境下建立了无人机着陆仿真系统及其分系统模型。通过仿真分析,该模型能够比较真实地描述无人机着陆过程的特性,为更深入地无人机仿真研究打下基础。
无人机,Matlab/Simulink,自主着陆,仿真
引言
飞行仿真本质上是通过实验手段进行技术研究[1],通过飞行仿真可以比较真实地模拟飞机的整个飞行过程,并获得其飞行过程中的各种姿态及参数的变化,可以对飞机的飞行过程进行更好的理论研究,降低研究风险,提高效率。
对无人机自主着陆过程的仿真,主要是研究无人机在着陆过程中的速度、高度以及飞行攻角的变化特性,以解决无人机自主着陆的安全问题和验证无人机自主着陆控制率的鲁棒性,确保无人机在外部环境变化的影响下自主着陆的精度控制在规定范围内。
Matlab/Simulink作为一款在动态系统建模和仿真方面应用广泛的软件,融合了科学计算、信号处理、图像处理等特点,利用它提供的航空模块可以使无人机飞行控制系统仿真变得方便直观[2]。无人机自主着陆六自由度仿真包含线性和非线性运算、多迭代解算等,仿真过程是一个复杂的系统建模仿真工程。而Matlab/Simulink在建模仿真方面的优点,决定了其在无人机自主着陆仿真方面具有较强的优势。
本文采用模块化设计思想[3],建立无人机非线性运动学和动力学模型,包括气动参数模型、发动机推力模型、六自由度运动学模型等,然后对各个子模型分别采用Simulink建立单元仿真模型。通过对单元仿真模型的集成得到了无人机运动的仿真模型,最后进行仿真并分析仿真结果。
1 无人机数学模型
无人机的空间运动是一个复杂的过程,在飞行和着陆过程中,其自身状态和外部影响都在不断变化,为了方便研究无人机的运动过程,对其作出以下假设:①认为无人机是刚体,而且由于无人机着陆过程时间比较短,质量变化很小,因此,可以假设其质量是常数;②假设地面为惯性参考系,即假设地坐标为惯性坐标;③无人机着陆过程离地面距离小,因此,可以忽略地面曲率,视地面为平面;④无人机着陆过程其高度较低,因此,可以假设重力加速度不随飞行高度而变化;⑤假设机体坐标系的x-o-z平面为飞机的对称平面,且飞机不仅几何外形对称,而且内部质量分布亦对称,惯性积Ixy= Izy=0[4]。
根据刚体动力学以及以上的假设可获得无人机机体坐标系下的6个动力学方程,如下所示[5]:

根据欧拉关系以及机体坐标系与地面坐标系之间的坐标转换关系,可获得无人机机体坐标系下的6个运动学方程。


根据这12个微分方程,可以描述无人机的六自由度运动模型。建模时,则可在Matlab环境下使用Simulink来构建上述无人机运动模型。
2 仿真环境总体结构设计
根据无人机的数学模型,作出简化处理,需要以下几个模块:飞行控制系统模块,环境模型模块(包括重力、标准大气压、风模型),无人机动力学方程模块,执行机构模块,气动力和力矩计算模块,发动机模块和气动参数计算模块[6-7]。各个模块间的关系,如图1所示。
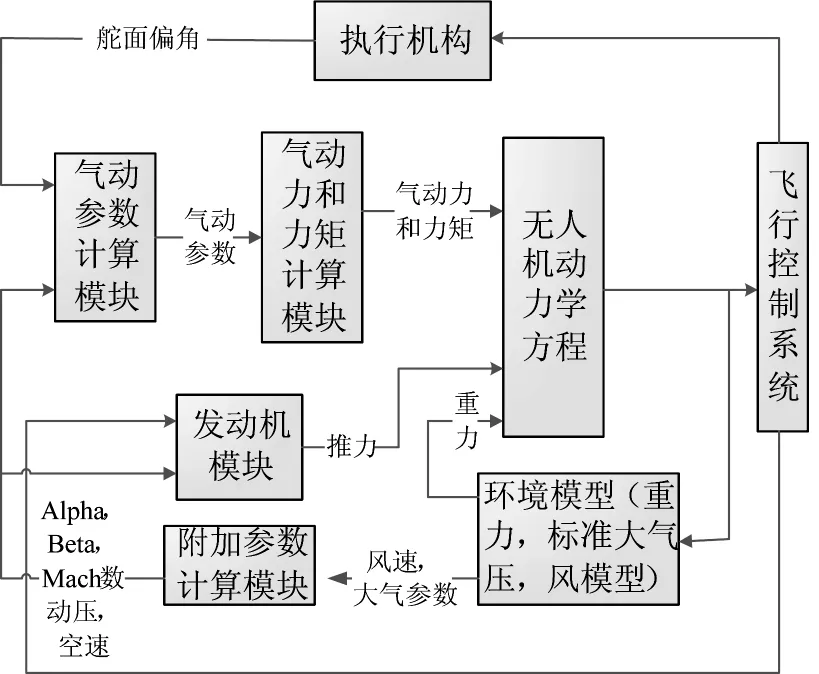
图1 无人机仿真系统组成框图
3 Matlab/Simulink建模
本文采用Matlab/Simulink对无人机进行建模,通过Simulink中提供的航空模块Aerospace Blockset,可以对无人机进行建模、集成与仿真。Aerospace Blockset将航空领域通用的标准模块在Simulink环境下进行集成,能够方便地组合并展示无人机的系统结构,在此基础上可以对无人机进行完整的系统开发和测试,从而完成无人机系统的概念设计。
3.1 无人机仿真模型
根据以上无人机仿真系统组成的框图在Matlab/Simulink环境下建立无人机仿真模型,如下页图2所示。
3.2 无人机动力学模型
无人机动力学模型采用Matlab的Simulink库中Aerospace Blockset中的6DoF(Euler Angles)模块,如下页图3所示,它只需在模块中设置惯性参考系下无人机的初始位置、速度、姿态角、滚转角速度、俯仰角速度、偏航角速度和无人机的质量。该模块的输入为无人机所受的合力和合力矩,输出为无人机的六自由度运动状态参数。

图2 无人机仿真模型

图3 无人机动力学模型
3.3 环境模型
环境模型为Environment Model模块,包括风模型、大气模型和重力模型;其中风模型包括风切变模型、Dryden紊流风模型和离散阵风模型,风模型如图4所示。大气模型采用 COESA Atmosphere Model模型,如图5所示。在该模型中输入地理高度,则可以利用标准插值算法计算出绝对的温度、气压和大气密度。重力模型采用标准的WGS84模型,此模型将地球当成椭球看待。重力场计算公式采用泰勒级数展开的形式表示,并封装成一个子系统。Environment Model模块,输入为无人机六自由度运动状态参数,输出为大气密度、重力以及其他大气环境参数;Alpha,Beta,Mach模块,输入为大气环境参数,输出为计算飞行过程中的攻角以及侧滑角,它的输出反馈回Atomic Subsystem模块[8]。

图4 风模型
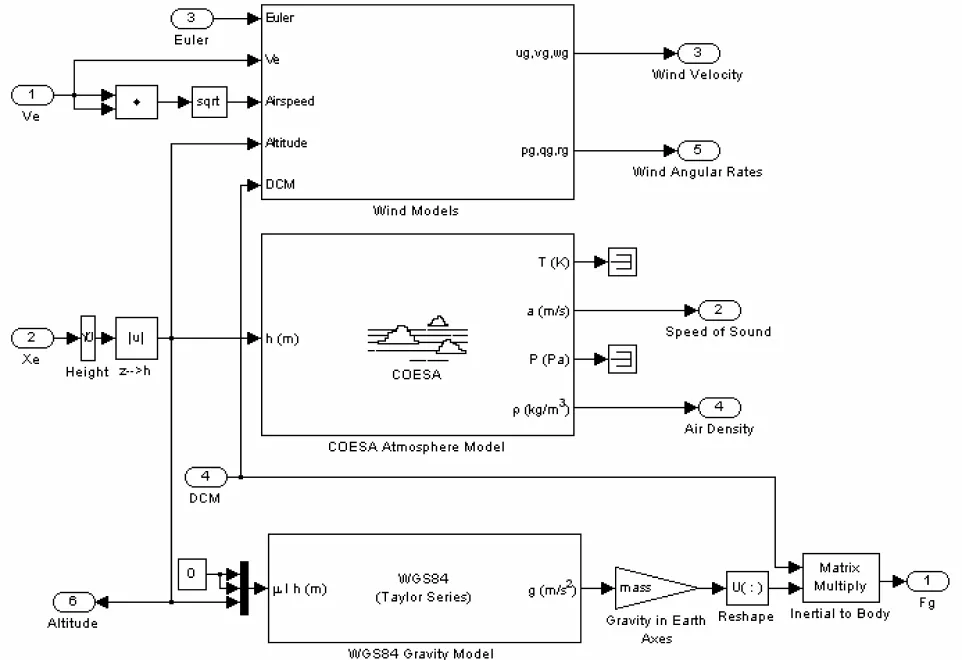
图5 大气环境模型
3.4 发动机模型
发动机模块为Turbofan Engine System模块,其输入为发动机油门杆的位置、无人机的马赫数和当前的无人机的高度,输出为推力和单位时间燃油消耗量。
3.5 气动力和力矩计算模型
Forces and Moments模块为气动力和力矩计算模型,输入为机身参数、动压和发动机推力,输出为气动力和力矩;其子系统模块如图6所示。采用Aerospace Blocket中 Aerodynamic Forces and Moments模块,该模块只需按照需要修改机身的参考面积、长度和宽度即可。在力和力矩子系统中,空气动力和机身的重力作用于机体中心的实时计算需要空气动力系数、推力、动压和参考机身参数。
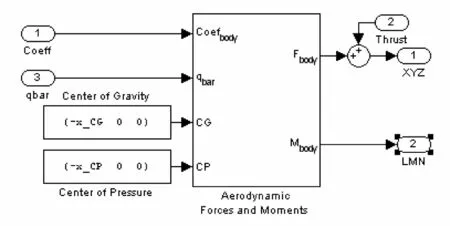
图6 Forces and Moments模块子系统
3.6 气动参数计算模块
气动参数计算模块为Atomic Subsystem模块,其输入为控制信号和空气动力系数,输出为无人机的各项力系数。
3.7 着陆引导模块
着陆引导模块的最终目的是让无人机以规定的精度跟踪预设的着陆轨迹。无人机着陆过程中,如果无人机偏离预设的着陆轨迹,雷达将测出的无人机实时位置发送给无人机,无人机根据实时位置与预设的位置进行比较,并计算出偏差,然后无人机以一定的控制规律控制角运动。其模块图如图7、图8所示。图7中根据无人机的实际距离X,经过预设着陆轨迹公式计算得出在X位置的预设高度,然后与实际高度比较,经计算得出无人机所需的俯仰角;在图8中,根据无人机所需的俯仰角与反馈的真实俯仰角进行比较,得出偏差,经计算,得出所需的舵面偏角。

图7 引导模块1

图8 引导模块2
4 着陆过程仿真
仿真系统采用某无人机气动数据,设置其初始条件:进场阶段以初始速度为[68 m/s,0 m/s,0 m/s]水平飞行,当无人机截获下滑信号时,此时无人机质心位置位于地面坐标系[-4 900 m,0m,-300 m]处,无人机开始进入下滑阶段,仿真开始,仿真结果如图9、图10所示。
图9中无人机从时间t=0时开始下滑,至高度为20 m时开始进入拉平阶段,无人机在t=68.8 s时着地;图10中无人机以-3°的轨迹角下滑,接地时其飞行攻角接近于零;图11中无人机以速度V= 68 m/s开始下滑,接地时其速度V=35.5 m/s;图12中无人机开始下滑时其竖直方向速度Vz=3.1 m/s,接地时其垂直速度Vz=-0.3 m/s,符合允许接地速度Hjd=-0.3 m/s~-0.6 m/s。将仿真结果与无人机实际着陆过程的速度、高度和飞行攻角进行比较,该结果能正确反应无人机真实着陆过程的运动参数变化特性。
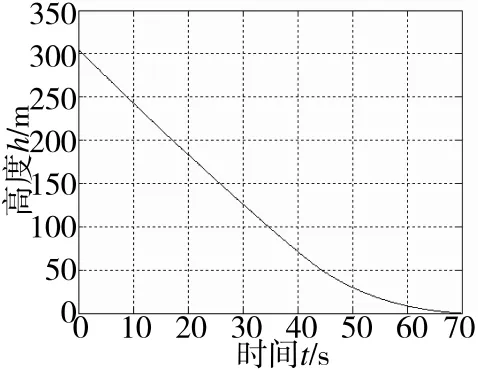
图9 某无人机质心位置纵向高度曲线
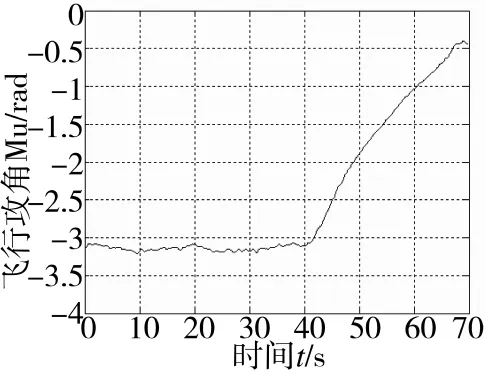
图10 某无人机飞行轨迹角变化曲线

图11 某无人机质心飞行速度曲线
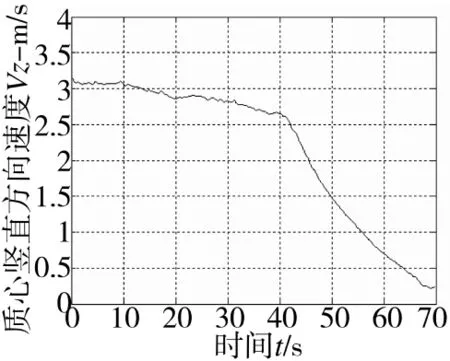
图12 某无人机质心竖直方向速度曲线
5 结 论
通过建立无人机非线性运动学和动力学模型,然后根据无人机仿真系统总体框图在 Matlab/Simulink环境下建立仿真模型,从而实现了无人机运动的计算机仿真,并对仿真结果进行了分析,验证模型能正确描述无人机自主着陆过程运动参数的特性,着陆精度在规定范围内。无人机整体模型由各个分模型通过集成后得到,结构清晰,容易对各个集成模块进行参数设置和调试,能够很好地实现无人机自主着陆过程的仿真。
另外,建立的无人机模型具有较强的通用性,可以对各个集成模块的参数进行修改后用于仿真其他类型的飞机。还可以对引导系统进行修改,用于多种其他方式引导的无人机自主着陆,如:精密进场雷达引导无人机自主着陆等。
[1]王永林.Matlab_Simulink环境下无人机全过程飞行仿真技术研究[D].南京:南京航空航天大学,2006.
[2]张坤峰.基于Simulink的导弹六自由度建模与仿真[J].舰船电子对抗,2011,34(4):72-76.
[3]李 辉,敬晓刚,徐利梅.基于Matlab/Simulink的运载火箭6自由度运动仿真[J].宇航学报,2005,26(5):616-619.
[4]张明廉,杨一栋.飞行控制系统[M].北京:航空工业出版社,1994.
[5]何湘智,王荣春,周 伟.基于MATLAB的无人机六自由度仿真与研究[J].机械工程与自动化,2010(4):32-34.
[6]张 镭,姜洪洲,齐潘国,等.基于MATLAB的飞行仿真[J].计算机仿真,2006,23(6):57-61.
[7]李文强,彭学峰,郑志强.基于Simulink的无人机六自由度仿真[J].系统仿真学报,2007,19(19):4604-4606.
[8]陈 斌,王 力.基于MATLAB的飞行控制实时仿真系统研究[J].微计算机信息,2007,23(5-1):295-297.
UAV Autonomous Landing Simulation Based on Matlab/Simulink
CHEN Xiao-fei,DONG Yan-fei
(School of Aircraft Engineering,NanChang HangKong University,Nanchang 330063,China)
In order toimprovethe safety and accuracyof UAV(Unmanned Aerial Vehicle)autonomous landing,andstudythealtitude,speed,andangleofattackchangesoffeaturesduringUAVautonomouslanding,it is needed to build the mathematical modeling of UAV landing.Using modular design concept.According to UAVnonlineardynamicsandkinematicsequations,UAVlandingsimulationsystemanditssubsystemsmodels in Matlab/Simulink environment are built.Through simulation analysis,the model can compare the real responseoftheactualcharacteristicsofUAVlandingandlaythefoundationforfurtherresearch.
UAV,matlab/simulink,autonomous landing,simulation
V271.4;E926.3
A
1002-0640(2014)11-0055-04
2013-09-05
2013-11-23
航空科学基金(2011ZA56001);江西省研究生创新专项基金资助项目(YC2011-S096)
陈晓飞(1987- ),男,江苏宿迁人,硕士研究生。研究方向:飞行仿真与效能评估研究。
