基于数据链的航空作战进程研究*

牛德智，陈长兴，徐浩翔，李永宾，王 卓

（1.空军工程大学理学院，西安 710051；2.空军工程大学装备管理与安全工程学院，西安 710051）

基于数据链的航空作战进程研究*

牛德智1，陈长兴1，徐浩翔2，李永宾2，王 卓1

（1.空军工程大学理学院，西安 710051；2.空军工程大学装备管理与安全工程学院，西安 710051）

研究了数据链支持下的航空作战兵力变化问题。将空战能力指数通过映射关系转化为平均战斗力水平，从数学理论上证明了二者具有等价性。结合平均战斗力水平，建立了基于数据链的改进蓝彻斯特空战模型及具有增援力量的作战模型。仿真分析了等效实力比、不同初始值以及增援时刻的不同对空战进程的影响，结果表明数据链具有提高作战效能和改变战局的作用。实验发现了在增援作战时，存在“局部最优增援时刻点”这一重要结论。

数据链，航空作战，蓝彻斯特，等效实力比，局部最优

引言

在信息化战争条件下，超视距空中作战已日渐作为现代空战的主要样式，在这一应用场景下，信息的获取变得至关重要［1］。数据链以其独特的战场态势共享、精确指挥控制和武器协同的无缝链接优势，在航空作战中发挥着中枢系统的作用［2］。近几场局部战争无不表明，数据链在现代战争中发挥出了巨大威力。美军从上世纪50年代开始研制数据链并先后将各种不同类型数据链运用到作战飞机上，其空中作战能力大幅度提高［3］。在这种环境下，开展数据链体制下的航空作战进程研究，对于预测整个空战进程、科学判断战斗结果以及合理作出指挥决策等，都具有重要意义。

纵观现有的文献研究成果，大多是针对数据链体制下的飞机效能评估问题，或者未考虑数据链作用，研究不同作战条件下的空战过程兵力变化情况，这些未能将效能评估的结果应用到实际的空中作战场景中去，造成了“由作战到评估效能，再由评估结果到作战运用”的环路没有有效粘合。文献［4］研究了通过雷达范围的变化之比来确定数据链作战效能的评估方法，为数据链效能评估问题提供了切入口。文献［5］将飞机各项指标分为有、无数据链信息支持两类进行评估，同样也仅限于评估出效能大小。文献［6］讨论了数据链支持下的空战双方飞机数量的变化问题，分析具有一定的合理性，但是模型中缺少一个直接反映数据链作用的量化指标，这样不利于直接研究数据链对空战双方格局的影响。文献［7］研究了不同条件下的兰彻斯特作战模型，未考虑信息因素（数据链）对战斗过程的影响，不适用于现代空战。

本文研究的出发点就是将作战效能评估的结果再应用到作战对决中，实现评估与作战之间关系的一体化。首先通过空战能力指数变换得到衡量飞机作战效率的平均战斗力水平，然后建立具有数据链特征的改进兰彻斯特模型进行空战进程的变化分析，设定具体的仿真样例来说明数据链对空战的影响，并对有增援情况下兵力支援的时间和数量关系进行了科学说明。

1 空战能力与平均战斗力水平

1.1 飞机对空作战能力指数模型

飞机的空战能力指数可以采用对数法进行计算，该方法简单易行，而且得到了广泛的认可。对数法选用有关空战的7个主要项目来衡量飞机的空对空作战能力。它们是火力、机动性、探测目标能力、生存力、电子对抗能力、航程和操纵效能。将前3项的对数值相加，最后乘上后4项系数即得出总的空战能力指数［8］，表示为：

其中，C为空战能力指数，A1为火力参数，A2为机动性参数，A3为探测目标能力参数，ε1为生存力系数，ε2为电子对抗能力系数，ε3为航程系数，ε4为飞行员操纵效能系数。

一般来说，单机对单机的空战损失比与飞机的空战能力指数成反比。在本文中，为了在兰彻斯特方程基础上研究飞机作战进程中的数量变化，特引入平均战斗力水平来反映飞机的杀伤能力，其在本质上和空战损失比、空战能力指数是一致的，只是它可以作为模型参数直接使用。

1.2 空战能力与战斗力水平的转化

由于飞机的火力参数、机动性和探测能力的数量级相对于其他4个参数都比较大，所以由式（1）及文献［4］知，空战能力指数一般远大于1。在空战中，考虑单机一次战斗只打击一架敌机的情况，则应该用单机的平均战斗力水平来衡量作战威力，其意义表示单机在单次作战中对敌机的杀伤效率。

作如式（2）的变换，将空战能力指数C变换为在区间（0，1）上的平均战斗力水平η（其中k为一比例调节因子，且k＞0，其作用是避免变换后的η在数值上过于集中）。

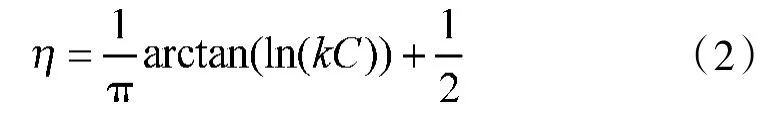
现证明η和C关于空战能力的描述是等价的，并且η和C具有一致性，即η随C的增大而增大，随C的减小而减小。

［证明］：令A={x|x∈Z，x＞0}，B={x|x∈Z，0＜x＜1}，做由A到B的映射：

所以，f:A→B是由A到B的一一映射，这样就说明，A和B是等势（等价）的，即A～B。

另外，可以求得

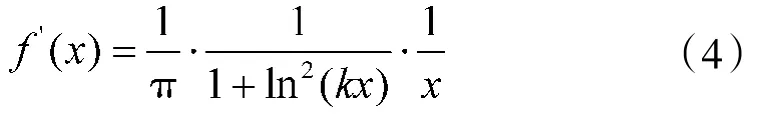
∵x＞0，∴f'（x）＞0

这说明f（x）为增函数，由此说明，在式（2）中，η随C的增大而增大，随C的减小而减小，η和C的变化关系一致。所以，η在保证空战能力指数特性的情况下，可以用来作为平均战斗力水平。

2 数据链支持下的蓝彻斯特方程

兰彻斯特方程（也称为兰彻斯特作战模型）是1914年英国工程师兰彻斯特在英国工程杂志上发表的一系列论文中提出，它是用微分方程描述的交战双方兵力变化关系［7，9］。兰彻斯特模型的主要优点是便于分析人员进行灵敏度分析，迅速改变兵力编成、装备特性等变量的结果，适用于各种规模的作战模拟。此处仅以兰彻斯特平方律方程（其他类似）进行分析，其方程为：

式中，t为时间，R、B分别为红、蓝军在时刻t的战斗单位数量，α、β分别为蓝、红军每个战斗单位的平均战斗力水平。对于此处的α和β，可以通过式（1）～式（2）来具体确定不同类型作战飞机的平均战斗力水平。

对上式进行等式相除后并进行积分，可以得到该微分方程组的状态解为：

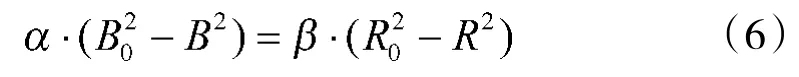
令x=1-R/R0表示红军兵力数量的消耗率，y= B/B0表示蓝军兵力数量的剩余率。L=β·R02/α·B02表示可以理解为衡量红蓝双方战斗实力的一个参数，即红蓝双方的战斗实力之比，L＜1时表示蓝军战斗实力强，L＞1时表示红军战斗实力强，L=1时两军的实力相等。将式（6）变形，并用x，y，L代入得：

按照式（5）～式（7）的分析方法，依然可以得到红方消耗率与蓝方剩余率的变化关系：

上式中的（1+λ）/（1-λ）·L部分可以理解为等效实力比。另外，在双方都采用数据链的情形下，可以将相对提升率融入到式（8）～式（9）中，且定义相对提升率为：

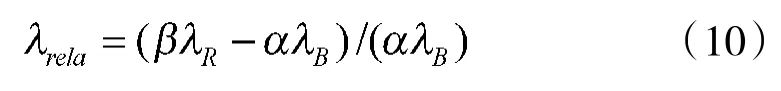
从式（10）可以看出，λrela为一个可正、可负的量，当为正时表示两方都采用数据链后红方的战斗力水平占优，当为负时表示都采用数据链后蓝方的战斗力水平占优，这样处理也是符合实际的。

在考虑一方兵力不足有增援的情况下（如红方），进一步可建立该情形下的兰彻斯特模型为：

在式（11）中，μ表示增援率（可以是恒定增援率，也可以是变化增援率），t0表示增援开始的时刻，ε（t）表示阶跃函数［10］，用它来限制仅当增援开始时，增援对兵力的变化才起作用。此处需要说明的是，模型（11）不管是在双方都采用数据链的情况下，还是双方都有空中增援力量的情况下，都可以进行扩展以适应不同的战斗状况。

3 仿真实验分析

3.1 数据链对消耗率与剩余率之间变化关系的影响

1982年，邓聚龙教授创立了灰色系统理论［6-7］，之后灰色系统理论被不断发展完善，在诸多领域都得到了应用［8］。一方面灰色关联、灰色统计、灰色预测、灰色控制、灰色评价等基础理论被逐步完善，另一方面灰色系统理论与其他领域交叉产生了一系列成果，如灰色博弈［9-10］、灰色粗糙集模型［11］、灰色神经网络模型［12-13］等。灰色系统理论之所以具有如此旺盛的生命力，在于其主要研究的“小样本不确定”灰色系统在客观世界是普遍存在且难以回避的［14］。本研究采用灰色聚类评估模型对生活垃圾分类投放方案进行评价。

此处，取一组红、蓝双方实力的参数为L=［0.3；0.5；1；1.5；1.7］，在该组参数下仿真红方的消耗率与蓝方的剩余率的变化曲线如图1所示。

图1 蓝军剩余率和红军消耗率的变化关系

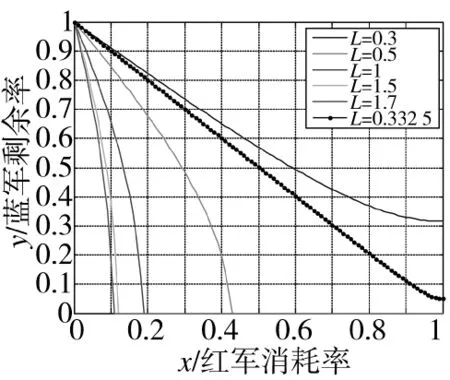
图2 红方引入数据链后的蓝军剩余率和红军消耗率的变化关系

由图1可以看出，当双方的实力相同（L=1）时，二者的变化规律一致（同消同亡），当L＜1时，红方的消耗率大于蓝方的剩余率，最终蓝方可以获胜；当L＞1时，红方的消耗率小于蓝方的剩余率，最终红方可以获胜。

同样在该组参数下，考虑红方引入数据链系统，这样设定λ=0.5，讨论这两种变化率的变化关系，仿真曲线如图2所示。由变化曲线的关系知，由于数据链对作战实力的影响，只有当红方实力很弱小（本次仿真图中为L=0.3）时蓝方可以取胜，其余的状况均为红方可以取胜。在L=0.3和L=0.5之间，采用“二分法”近似找到了二者的实力均衡点为L=0.332 5，并绘出消耗率与剩余率曲线如图2所示。

分析图中曲线变化关系知，在数据链体制下，红方只要保持与蓝方的实力比大于L=0.332 5，就可以最终获得空战的胜利。这说明，对于空战中的双方，实力较弱的一方通过引入数据链终端，就可以赢得战斗主动权进而取得胜利。

3.2 数据链体制下的空战进程变化实验

为了综合体现本文的方法思想，首先设定一种作战场景（红少红弱），红方拥有F-14A机型10架，蓝方拥有F-15E机型15架，双方进行空中作战，并且在兰彻斯特平方律模型下进行研究。采用文献［4］中的作战飞机各项指标，由式（1）可以求得空战能力指数分别为13.4和19.8。这样，按照本文中提出的式（2）的变换方法（取k=1/10），可以得到两种飞机的平均战斗力水平大约分别为α=0.7和β=0.6。在这种情况下，对微分方程组（5），采用Runge-Kutta数值积分求解方法，在matlab中通过编程可以仿真得到红、蓝双方的战斗动态损耗曲线，如图3所示。

图3 战斗过程中的红蓝双方动态损耗图

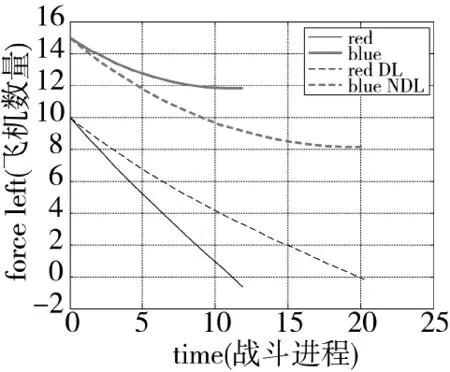
图4 数据链作用下的双方动态损耗图

该条件下最终获胜的为蓝方。考虑数据链的引入，使得红方的平均战斗力水平提升30%，即λ=0. 3，同样可以得到双方的动态损耗关系（图4）。虽然结局仍为红方失败，但是数据链机制的引入，延缓了红方失败的时间，在战术应用中，就可以采用延长的作战时间等待来援等因素以寻求改变战局。

这样，以下主要讨论红方在拥有增援时的双方力量变化，主要分析不同的初始条件及增援起始时间对空中战局的影响。

3.3 增援力量对空中战局的实验分析

仍然是3.2中的仿真参数，并且设定增援率为2.5。这样在考虑红方有增援力量（增援从t0=0开始）的情况下，分红方飞机有、无数据链支持，可以仿真得到红蓝双方的空战动态损耗图（图5）。为了便于比较和说明问题，也同时绘制出无增援时的作战双方动态损耗曲线（图4中的曲线）。

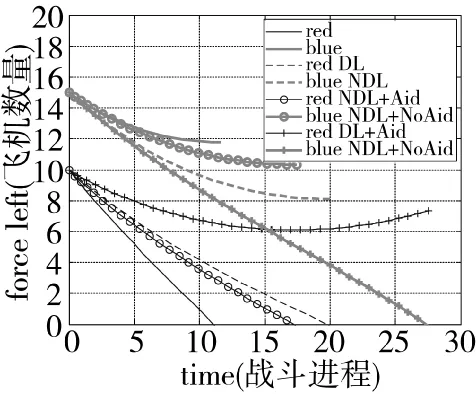
图5 不同作战条件下的双方动态损耗图

图6 随R0初始数量不同时双方的动态损耗图

上图中的4种类型的动态损耗曲线分别对应双方最原始的作战样式、红方有数据链支持时的作战样式、红方无数据链支持但有增援的作战样式、红方有数据链支持并且有增援。由图6可以看出，红方在有数据链支持下，可以利用延长的作战时间等待空中支援力量，最终可以改变劣势获得胜利。相反，红方在本来实力就弱于蓝方的情况下，不采用数据链体制，单纯依靠一定速率的支援并不能改变失败的战局（空战中红方剩余飞机数量为0时即认为失败，增援不再继续）。

接下来考虑红方有数据链支持且有增援，但初始的整体实力仍弱于蓝方时（由等效实力比可以计算得到，当R0不大于11时红方实力弱于蓝方），不同的飞机初始数量与获得战争胜利时损失的飞机数量之间的关系。蓝方飞机数量和红方增援率保持不变，令红方飞机初始数量分别为R0=［8，9，10，11］，可以得到此时的飞机数量变化曲线，如图6所示。

R0初始数量越大时，越能较快地加速空战进程获得胜利。图中还给出了当R0=12时的双方动态损耗曲线，此时红方实力大于蓝方，不需要增援力量就可以获胜，这也说明了等效实力比的合理性。另外，表1列出了在不同的初始数量时到战争取胜红方支援的飞机数量和损失的飞机数量，由表中的数据也能说明这种规律，并且初始R0较大时，需要增援和损失的飞机数量都相对较少。

表1 红方不同初始值时的支援和损失飞机数量

进一步，讨论不同的增援时刻对于空战过程的影响。取3.2中的仿真参数，让t0在［0，12］之间取值，步进量为1，得到的双方动态损耗曲线，如图7所示。

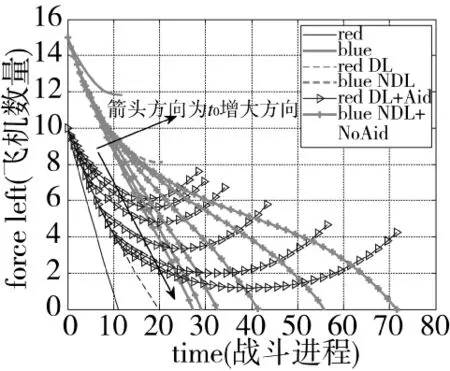
图7 不同t0时的双方动态损耗图

图8 t0值不同时的红方增援和损失飞机数量变化

由图7可知，当t0增大时（即增援开始时刻越晚），总的趋势是双方的空战进程维持时间越长，战斗胜利时红方剩余的飞机数量越少，但是由于一些相邻时间上的各种飞机数量比较接近，所以，此图像不易分析过程中的红方增援和损失飞机数量变化情况。因此，这里专门给出随t0值变化时的红方增援和损失飞机数量曲线（图8）。

从图中可以看出，随t0值变化时，增援和损失的飞机数量并不是简单的单调递增关系，而是存在增援和损失飞机数量的一系列极小值点，在这些极小值点周围，增援和损失的飞机数量都较大。据此可以得出结论，在不同的增援时刻，存在使得增援和损失飞机数量同时较小的局部最优点，本文将之称之为“局部最优增援时刻点”。掌握了这种时刻点，可以便于指挥员对整场空战中在何时进行空中力量支援，使得空战结束时损失的飞机数量最小提供决策依据，这对于把握空中战机和合理利用飞机资源具有重要意义。

4 结论

本文对数据链体制下的航空作战进程预测及分析问题作了相关研究。从飞机作战效能评估角度出发，将飞机空战能力指数转化为平均战斗力水平，进而建立了表征数据链影响作用的改进兰彻斯特空战模型及其有支援情况下的空战模型。定义了等效实力比，并对有、无数据链情况下的一方消耗率与另一方剩余率之间的变化关系进行仿真分析。数据链的引入，使得实力较弱一方可以通过等待增援飞机来实现空中战局的扭转，并且通过发现了“局部最优增援时刻点”来为决策人员掌握和运筹整个过程提供了重要依据，该结论对如何安排和部署空战具有启示意义。

［1］王安丽，何胜强，张 安.机群编队对地攻击飞机武器系统作战模型研究［J］.飞行力学，2005，23（1）:82-85.

［2］Enel L，Guillem F.Improvements in Navy Data Networks and Tactical Communication Systems［J］.World Academy of Science，Engineering and Technology，2006（18）：97-101.

［3］Gray，Frank B，L'Hommedieu，William R.A Combat-effectiveness Approach to Information Assurance［C］//U.S.Air Force T and E Days 2010，2010：355-362.

［4］黄金才，张 勇，杨 磊，等.战术数据链作战效能定量评估方法［J］.火力与指挥控制，2010，35（12）:66-69.

［5］陈卫平，姚佩阳，张志坚，等.基于数据链的空战效能评估［J］.火力与指挥控制，2008，33（6）:70-73.

［6］夏白桦，周于义.数据链对现代空-空作战效能的影响分析［J］.计算机工程，2011，37（9）:257-260.

［7］巨金川.兰切斯特方程的推广及其作战应用［J］.电光与控制，2009，16（10）:22-25.

［8］徐浩军，郭 辉.空中力量体系对抗数学建模与效能评估［M］.北京：国防工业出版社，2010.

［9］ He J，Shang Y D.Operational Effectiveness Analyses of Air-to-Ground Strike for Battle-Plane［J］.Journal of Beijing University of Aeronautics and Astronautics，2002（5）：354-357.

［10］Zhou L，Zhang H Y，Wang T，et al.Static Check of WS-CDL Documents［J］.IEEE International Symposium on Service-Oriented System Engineering，2008（8）：142-147.

Study on Air Combat Process Changes Based on Data Link

NIU De-zhi1，CHEN Chang-xing1，XU Hao-xiang2，LI Yong-bin2，WANG Zhuo1
（1.Science College，Air Force Engineering University，Xi'an 710051，China；
2.Equipment Management and Safety Engineering College，Air Force Engineering University，Xi'an 710051，China）

Force changes problem in air combat based on data link is studied.Operation ability index is converted to average battle effectiveness level，whose equivalent property is proved by mathematic theory. According to average battle effectiveness level，improved lanchester air combat model and operation model with reinforcement based on data link is set up.Simulation analyzes how equal force ratio，different initial values and different reinforcement time influence the process of air combat，which shows data link could improve combat effectiveness and change combat result.Also，one important conclusion that there exists local optimum reinforcement time is found in case of battle with reinforcement.

data link，air combat，lanchester，equal force ratio，local optimum

V271

A

1002-0640（2014）11-0022-05

2013-08-05

2013-11-10

陕西省电子信息综合集成重点实验室基金资助项目（No.201107Y16）

牛德智（1984- ），男，陕西富平人，博士。研究方向：通信系统与雷达信息处理。