一类三种群时滞捕食－食饵系统的持久性①

王 锐， 王 奇， 张友梅

(1.安徽大学数学科学学院，安徽合肥 230601;2.合肥职业技术学院，安徽巢湖 238000)

近年来，很多研究者对具有功能反应函数的捕食－食饵系统开展研究，得到丰硕的成果.其中，功能反应函数既有只依赖于食饵的Holling型功能反应函数，也有像同时依赖食饵与捕食者的比率依赖型功能反应函数[1～6].Beddington[7]和 DeAngelis[8]曾经研究过一种具有 Beddington－ DeAngelis型功能反应的捕食－食饵系统:

受以上论文的启发，本文研究一类具Beddington－DeAngelis型功能反应的三种群时滞捕食－食饵系统:

其中，x1(t)，x2(t)，x3(t)分别表示食饵及两类竞争捕食者的种群密度，其分 τ1，τ3，τ5≥0 别表示对于食饵对捕食者产生的负反馈作用，τ2，τ4表示捕食者由于出生而产生的时滞，τ={τj(t)}，j=1，2，3，4，5，aj(t)表示种群 xi(t)的内禀增长率，b1(t)表示食饵种群内部的竞争率，b2(t)，b3(t)分别表示捕食者x1(t)，x2(t)相互间竞争率，并且函数 ai，bi，ci，di，αi，βi，γi，i=1，2，3 都是定义在R+上的严格正的连续有界ω－周期函数.

1 预备知识

定义2.1[9]称系统(2)是持久的，如果存在正常数mi，Mi(0＜mi＜Mi)，以及有限时间T，对所有的t≥T，均有以下结论成立:mi≤xi(t)≤Mi，i=1，2，3.

引理 2.2[10]如果:

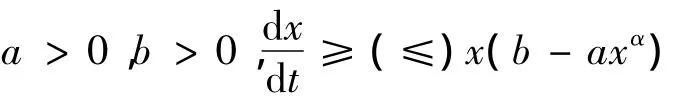
这里α是正常数，则:

下面给出文中用到的一些记号:

对连续有界ω－周期函数f(t)，记

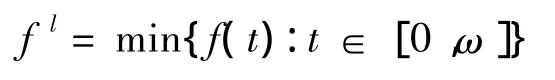
fu=max{f(t):t∈[0，ω]}

2 系统的持久性

定理3.1 如果系统(2)满足以下条件:

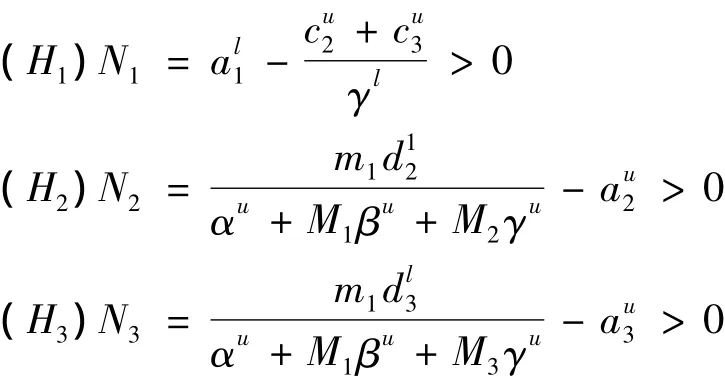
那么系统(2)是持久的，即，存在T＞0，当t＞T时，系统(2)的任意解都满足:mi≤xi(t)≤Mi，i=1，2，3，其中，

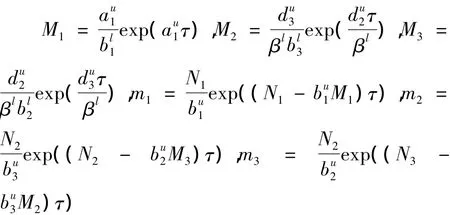
证明: 由系统(2)的第一个方程有:

将(4)从t－τ1到t上进行积分，得到:

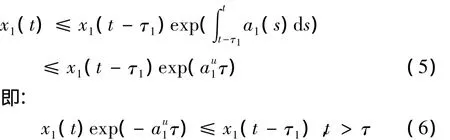
将(6)代入至系统(2)的第一个方程有:

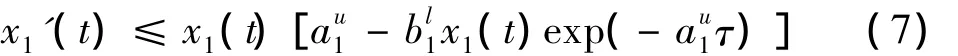
由引理2.2知:∃T1＞ 0，当t＞ T1时，有:

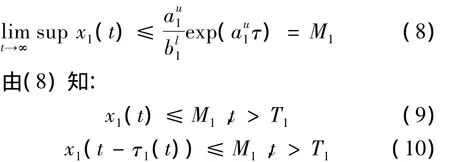
同时将系统(2)的第二个，第三个方程进行放大，得到:

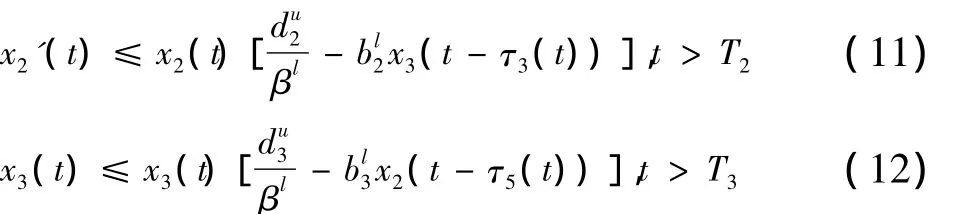
设x2(t)是x2(t)的最大值，代入(11)有:

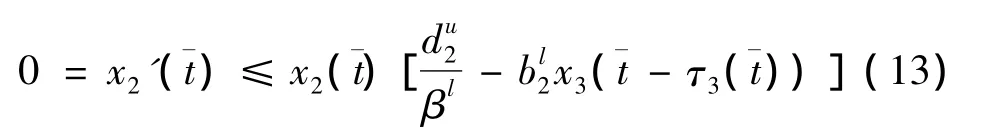
由于x2(t)≥0，解得:

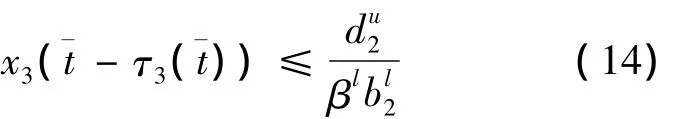
设x3()是x3(t)的最大值，代入(12)有

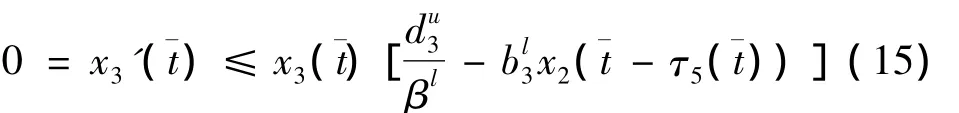
由于x3(t)≥0，解得:

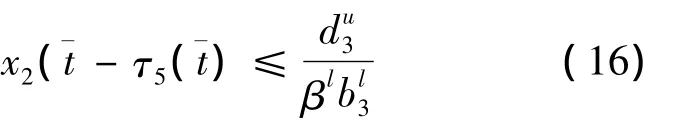
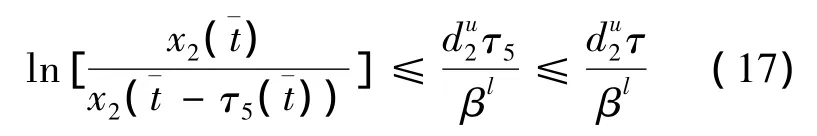
联合(16)与(17)得到:

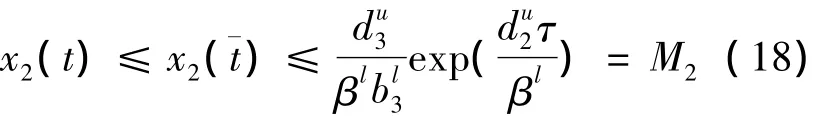
联合(14)与(19)得到:

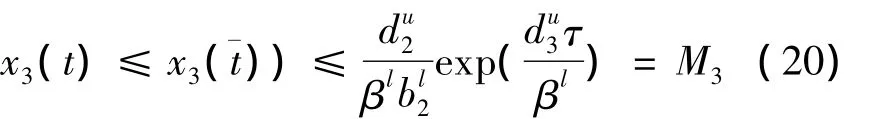
由(9)，(10)，(18)，(20)知，存在 T4＞max{T2，T3}，有:

设x1()为x1(t)的最小值，因此有:

由于x1()≥0，解得:

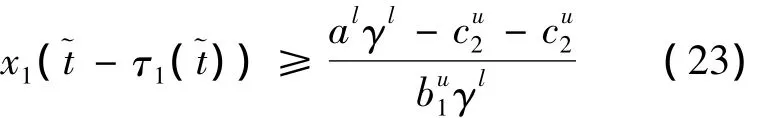
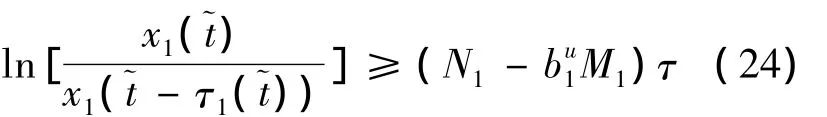
由(23)，(24)可以联合解得:

那么，存在T4＞0，当t＞T4时，有

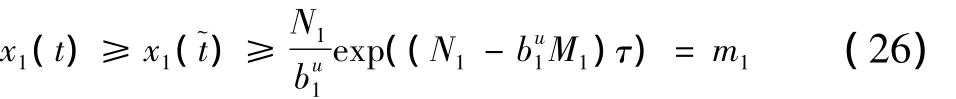
将系统(2)的第二，第三个方程进行缩小，可

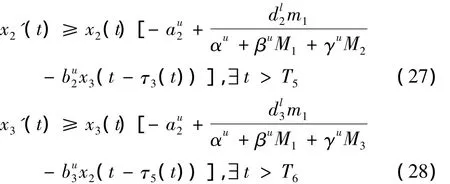
以分别得到以下两个不等式:设x2()，x3()分别是x2(t)，x3(t)的最小值，

代入至(27)，(28)分别得到:

仿照前面的解法，解得:

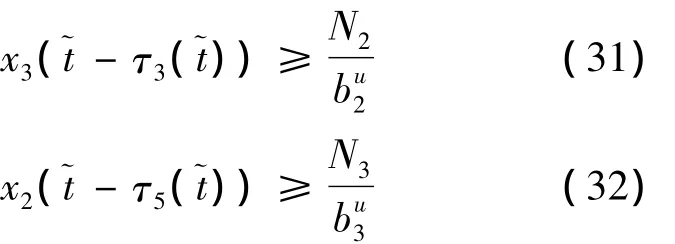
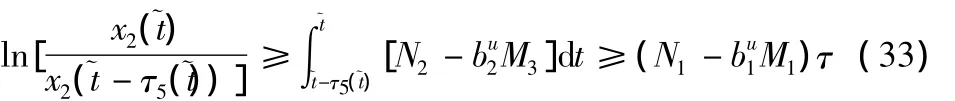
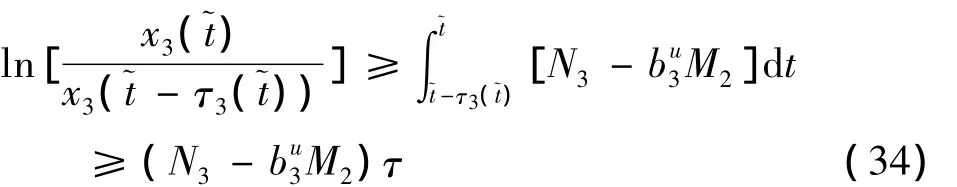
把(31)，(32)分别代入(33)，(34)中，分别解得以下两个不等式:

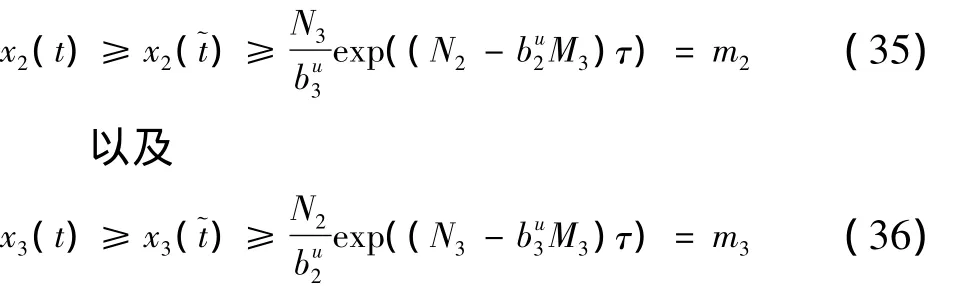
所以，有 T ＞ max{T1，T2，T3，T4，T5，T6}＞ 0，使得:mi≤ xi(t)≤ Mi，i=1，2，3，至此，系统(2)的持久性得证.

[1]R.Arditi，H.R.Akcakaya.Underestim－ ation of mutual interference of Pred－ ators[J].Oecologia，1990，83:358－361.

[2]R.Arditi，N.Perrin，H.Saiah.Functi－ onal Response and Heterogeneities:An Experimental Test with Cladocerans[J].O－ ikos，1991，60:69－75.

[3]C.Jost，R.Arditi.From Patternt Process:Identifying Predator－Prey Interactions[J].Popul.Ecol，2001，43:229－243.

[4]C.Jost，S.Ellner.Testing for Pred－ Ator Dependence in Predator－ Prey Dyn－ Amics:A Nonparametric Approach[J].Proc.R.Soc.Lond.Ser，2000，B267:1611－1620.

[5]G.T.Skalski，J.F.Gilliam.Functional Response with Predator Interference:Viable Alternatives to the HollingtypeⅡModel[J].Ecology，2001，82:3083－3092.

[6]P.M.Dolman.The Intensity of Inte－ Rference Varies with Resource Density:Evidence from a Field Study with Snow Buntings[J].Plectroph.Niv.Oecologia，1995，102:511－514.

[7]J.R.Beddington.Mutual Interferen－ Ce between Parasites or Predators andits Effect on Searching Efficiency[J].Anim.Ecol，1975，44:331－340.

[8]D.L.DeAngelis，R.A.Goldstein，R.V.O’Neill.A Model for Trophic Interac－ tion[J]，Ecology，1975，56:881－892.

[9]宋新宇，郭红建，师向云.脉冲微分方程理论及其应用[M].北京:科学出版社，2011.

[10]C.Shen.Permanence and Global At－ Tractivity of the Food－Chin System w－ith HollingⅣType Functional Respon－se[J].Appl.Math.Comput，2007，194:179－ 185.