基于AHP的智慧社区商品综合评价①

刘 红， 傅 军， 邓 伟

(1.成都理工大学管理科学学院，四川成都 610059;2.数学地质四川省重点实验室，四川成都 610059)

0 引言

随着互联网和信息技术的发展，越来越多的国家更注重智慧城市的发展，2006年，新加坡提出“智慧国2015”计划;2009年9月，美国迪比克市与IBM共同宣布，通过采用一系列IBM新技术“武装”的迪比克市将完全数字化，并将城市的所有资源都连接起来，侦测、分析和整合各种数据，并智能化地作出响应，服务于市民的需求.我国深圳、上海、广州、北京等城市智慧社区发展较快，北京西城区“智慧社区”社会服务管理平台，包括智慧中心、智慧政务、智慧商务、智慧民生四大部分14个子系统.

智慧社区电子商务系统主要为社区居民家庭提供与日常生活密切相关的消费品，该服务克服传统电子商务消费群体规模大，消费品范围模糊，比价单一的缺点，本文为购物者提供商品更智能的比价功能，从多方面对商品进行综合比价.智慧社区的电子商务系统，提供商品的选购功能，通过综合比较商品的价格、销量、商家的评分、商品的质保、商家的开店时间等，进行商品排序，从而用户可以最先查看到所要选购商品中性价比最高的商品.

本文采用AHP方法可以把复杂问题分解成不同组成因素，又将这些因素按支配关系分组形成阶梯层次结构，通过两两比较确定诸因素的相对重要性，然后综合有关人员的判断，从定性与定量的角度，将实际问题层次化、数量化.

1 商品比价层次结构模型

根据若干商品购买指标，结合电子商务网站的特征，最后征求有网络购物经历的人的意见，从而确定目标层、准则层和方案层，商品比价层次结构型如图1所示.

2 构造成对比较阵

根据比较标准确定对比矩阵如下:

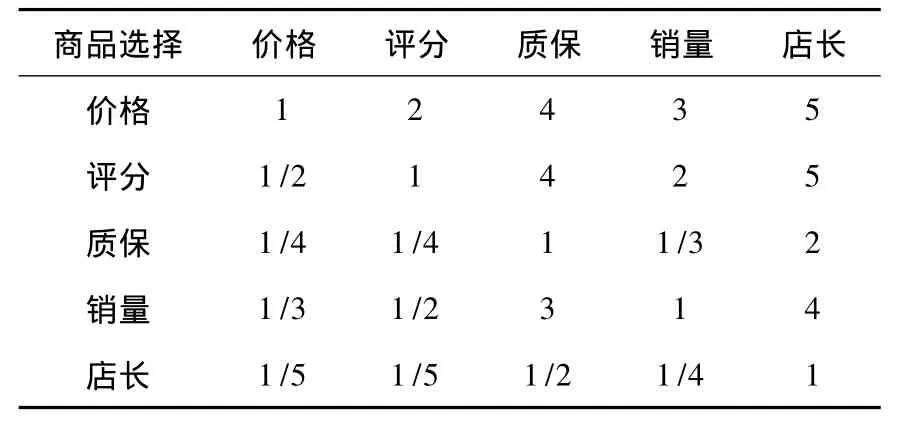
表1 准则层对于目标层的判断矩阵

得到该判断矩阵可以简化为式(1).

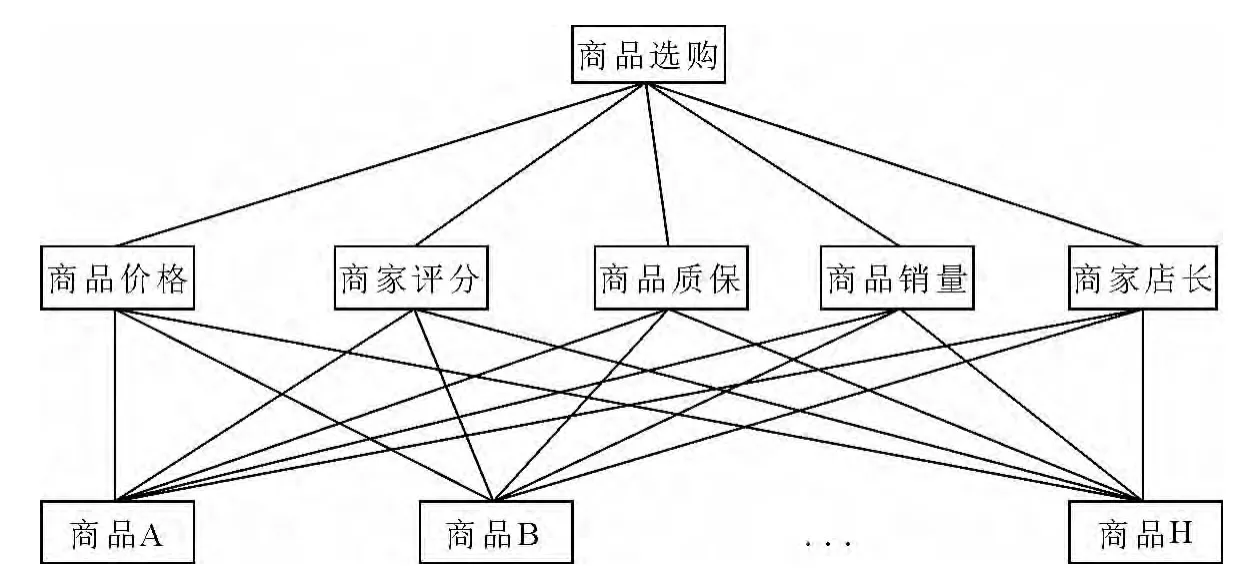
图1 商品比价层次结构模型

3 计算权重向量

关于 n阶正矩阵 A=(aji)，若对所有的 i，j，k∈I={1，2，…，n}满足aij=aik/ajk，则称A是具有完全一致性的[1].当矩阵 An×n是一致矩阵时，矩阵的最大特征值正是矩阵An×n的行数，即λ =n，其余n－1个特征值均为0，任一列(行)都对应于特征值λ的特征向量.若成对比较矩阵是一致性矩阵，则取对应于最大特征值n的归一化特征向量{w1，w2，…，，其中wi表示下层第i个因素对上层某个因素影响程度的权值.若成对比矩阵不是一致阵，要取其最大特征值对应的归一化特征向量作为权向量 w，则 Aw=w，w={w1，w2，…，wn}[2].

在层次分析法中，式(1)所示矩阵A中，aij≠aik/ajk，因此矩阵An×n不是一致矩阵，因此使用特征值法来计算权向量.应用Excel进行特征值法计算层次分析法所需要的值，计算判断矩阵每一行的乘积，计算公式为aij，计算各行Mi的n次方根公式对向量 W=(W1，W2，…，Wn)T做归一化处理，即即为我们所要求的指标权重系数值[3].利用上述方法计算得到各项指标的权重系数值如下表2所示.

表2 各项权重系数值

检验An×n的一致性程度，如果矩阵An×n的最大特征值λmax比n大得越多，An×n的不一致性越严重.因而根据λ－n数值来衡量矩阵An×n的不一致程度.建立一致性指标CI=(λmax－n)/(n－1)，可知，CI越大，表示An×n的不一致程度越严重.其中然而对于一个具体的矩阵来说，很难判断移植性指标CI到底是很大还是很小，针对这个问题采用随机RI一致性指标来检验判断矩阵An×n是否具有满意的一致性.一致性比率CR=CI/RI，如表3所示.

表3 平均随机一致性指标RI的数值

在本商品比价层次结构中，针对矩阵An×n，用上述方法计算得到 λmax=5.1395，因此，An×n的一致性指标CI=0.0348，对于方案层有八种情况，由表 3 可知，RI=1.41，从而得到 CR=0.0311，即CR ＜0.1，一般认为CR ＜0.1时，判断矩阵具有满意的一致性，因此矩阵An×n具有满意的一致性.

4 计算组合权向量

在计算组合权向量之前，需要将方案层相对于准则层的每个准则进行对比，矩阵如下表

表4 方案对于价格准则的判断矩阵

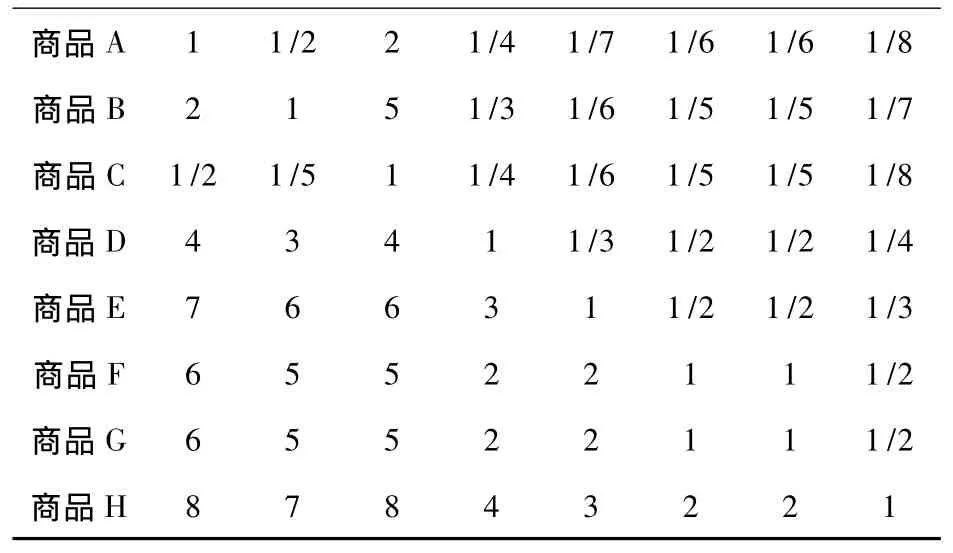
A 1 1/2 2 1/4 1/7 1/6 1/6 1/8商品B 2 1 5 1/3 1/6 1/5 1/5 1/7商品C 1/2 1/5 1 1/4 1/6 1/5 1/5 1/8商品D 4 3 4 1 1/3 1/2 1/2 1/4商品E 7 6 6 3 1 1/2 1/2 1/3商品F 6 5 5 2 2 1 1 1/2商品G 6 5 5 2 2 1 1 1/2商品商品H 8 7 8 4 3 2 2 1

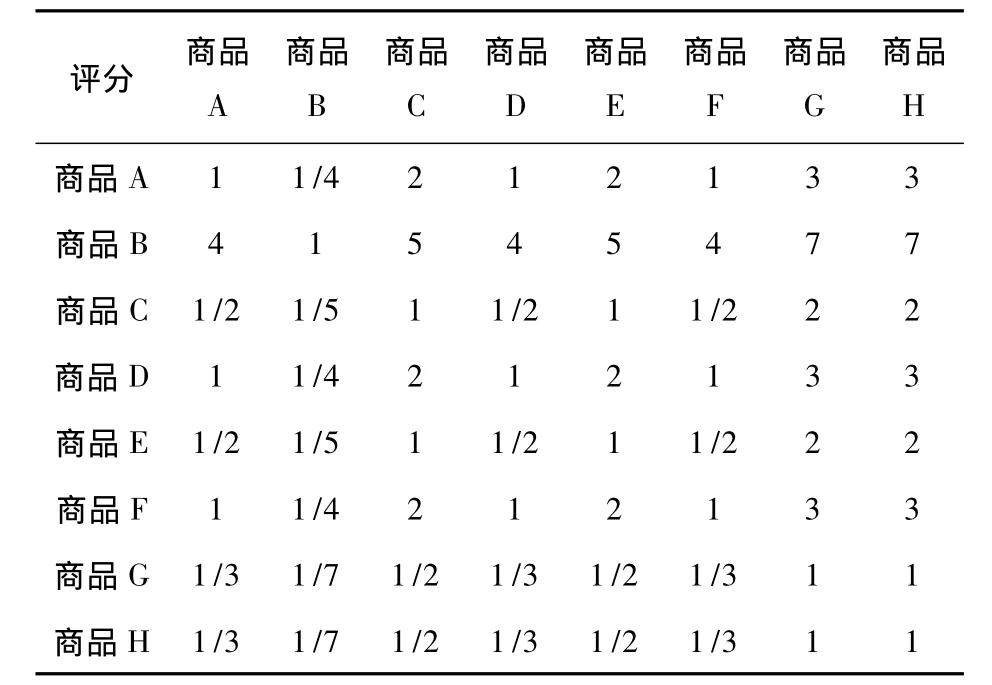
表5 方案对于评分准则的判断矩阵

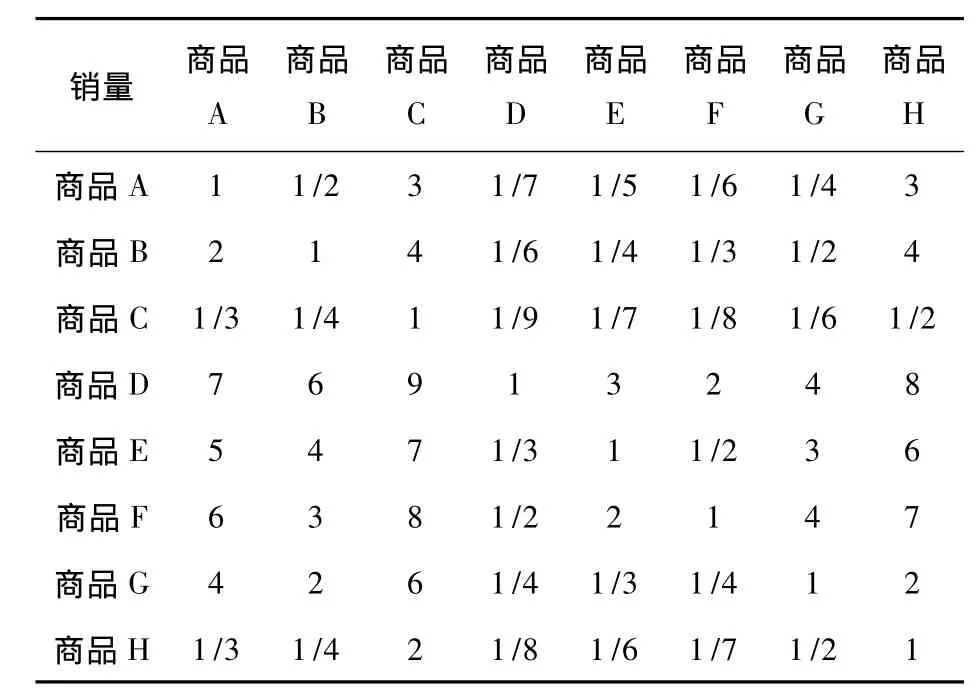
表6 方案对于销量准则的判断矩阵

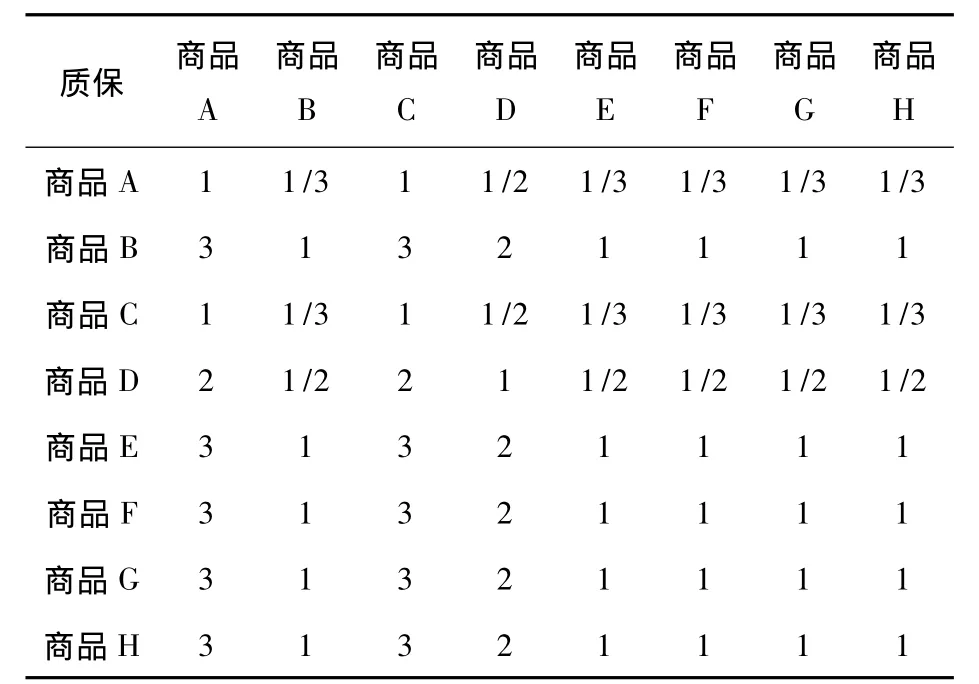
表7 方案对于质保准则的判断矩阵

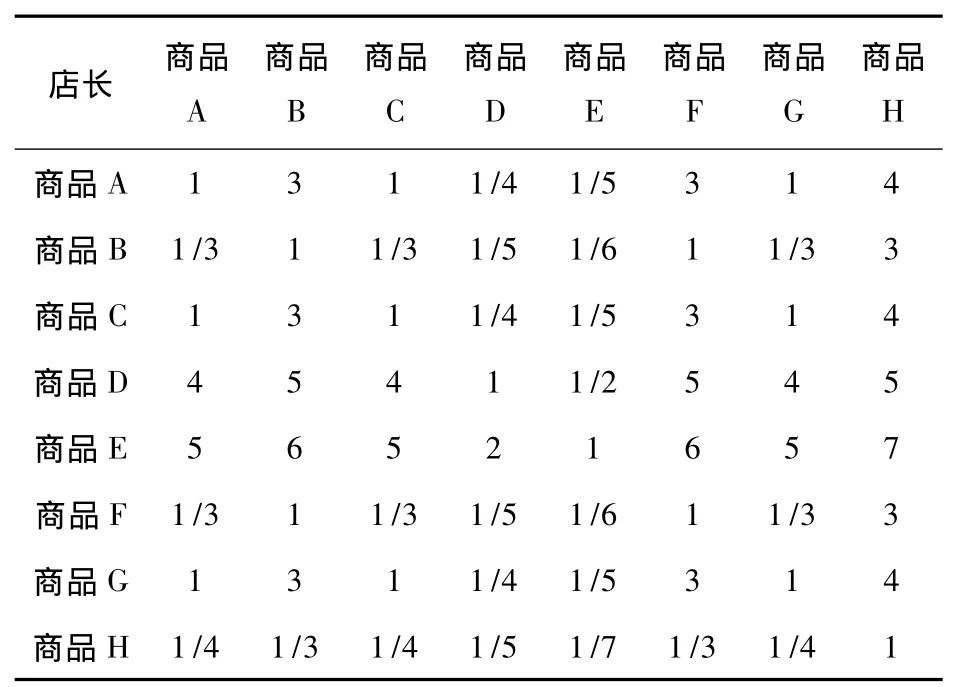
表8 方案对于店长准则的判断矩阵

得到方案对价格准则的权重及一致性判断如表9所示.表9为对应价格、评分、销量、质保、店长准则的判断矩阵得到的权值及一致性检验的参数CI，RI的值.

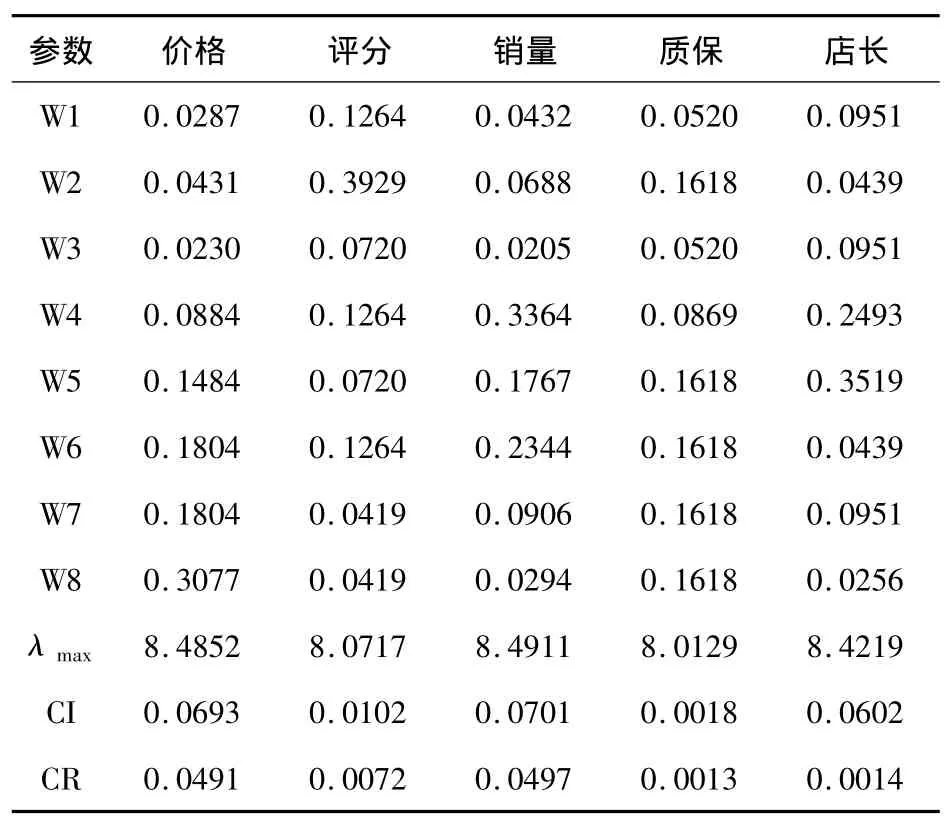
表9 方案层相对于准则层的参数值

最后，计算层次总排序，层次总排序计算表如表10所示.

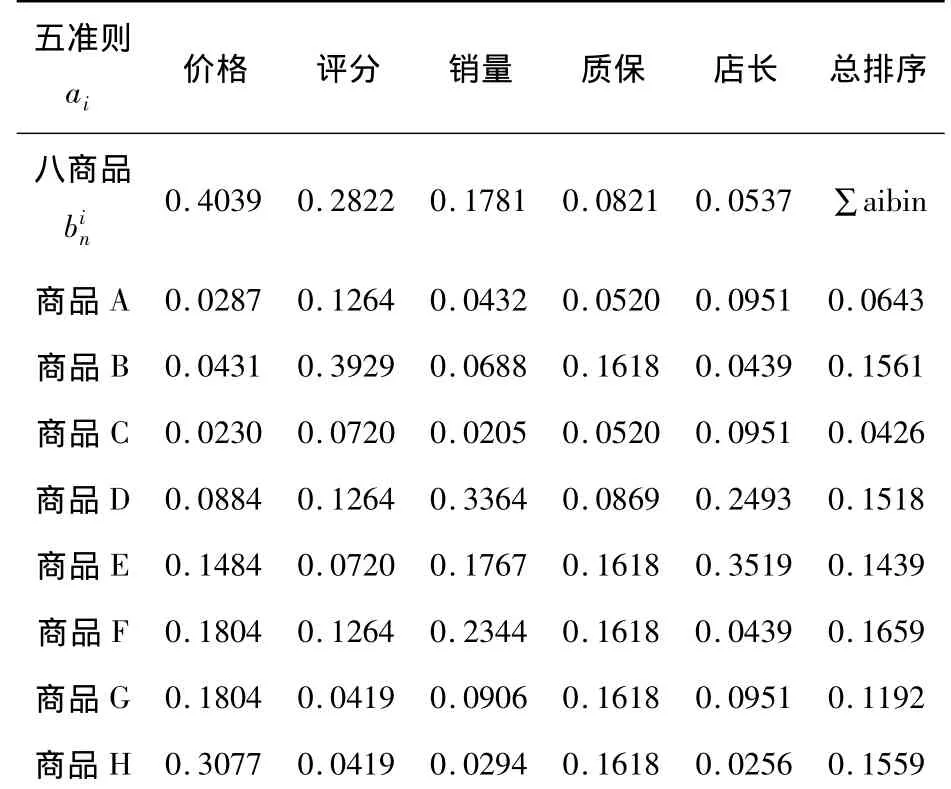
表10 层次总排序计算

以下，对层次总排序进行一致性检验，CI=0.0467，CR=0.0331，因为CR ＜ 0.1 ，所以得到总排序也满足一致性.这样，无论单排序还是总排序均满意一致性，排序结果符合实际情况.商品的最终排序为F＞B＞H＞D＞E＞G＞A＞C，即可以按照这个顺序排列商品显示顺序.

这样通过使用层次分析法，就可以将商品排序显示给用户，可以大大节省用户查找商品的时间，方便了用户的操作.

5 结论

智慧社区电子商务系统是互联网创业热潮中非常活跃的一种形态，该服务提高了人们的生活质量.智慧社区服务的智能化，高效化成为人们选择该服务的主要依据，基于AHP的商品综合评价可以从多方面有序地反映商品比价，让人民更好，更准确选择所需产品，更好的满足消费者需求，实现了优质服务的宗旨.

本文结合理论和实际，充分证明了AHP在智慧社区电子商务系统商品综合评价中应用的科学性和有效性，为今后智慧社区电子商务系统提供了更好的选购功能，为社区住户、加盟商、物流提供了重要的信息，充分显示了信息产业的优势.

[1]孙宏才，田平，王莲芬.网络层次分析法与决策科学[M].2011，20－30.

[2]He Kun.A Study on the Scale of Analytic Hierarchy Process[J].SYSTEMS ENGINEERING－－－ THEORY ＆ PRACTICE，1997，6:58－61.

[3]储敏.层次分析法中判断矩阵的构造问题[D].南京:南京理工大学，2005.

[4]先锋.用电子表格(Excel)实现层次分析法(AHP)的简捷计算[J].中国科技论文，2004，5.

[5]洪志国，李焱.层次分析法中高阶平均随机一致性指标(RI)的计算[J].计算机工程与应用，2002，12:45－48.

[6]费小燕.层次分析法在第三方物流服务商评价中的应用研究[J].商业经济，2010，16.

[7]李礼.建筑材料绿色性的6E综合评价体系研究[D].大连:大连理工大学，2012，10.

[8]谢莉琴.基于层次分析法的省级新农合运行管理评价指标体系构建研究[D].北京:北京协和医学院，2013，01.

[9]王生，凌胜利.层次分析视角下中国软实力战略问题研究[J].社会科学战线，2012，10.