无标度网络中的SIS模型的计算机模拟①

续 婷， 朱 烽

(1.中北大学 理学院，山西太原 030051;2.太原科技大学 应用科学学院，山西 太原 030024)

0 引言

传染病是一种扩散性极快的疾病，对人类健康有极大的威胁.近些年的几起大的传染病，对世界产生了极大影响.

1998年6月，美国康奈尔大学理论及应用力学系的博士生Watts及其导师Strogatz在Nature杂志上发表了题为《“小世界”网络的群体动力行为》的文章[1].而经典的SIS模型是建立在这种网络下的，即人际网络是一个均匀网络.同时传染性与恢复性是按照固定比例完成的.但在现实世界中这些是很难满足的.

1999年10月，美国圣母大学物理系的Barabasi教授及其博士生Albert在Science杂志上发表了题为《随机网络中标度的涌现》一文，揭示了复杂网络的无标度特性，并建立了无标度网络的模型[2，3].

因为无标度网络的优先连接性，所以对于现在世界的互联网与民航网络都是典型的无标度网络，由于网络的复杂性，建立确切的传染病模型是很困难的，同时即便建立起模型，对其的研究也是不容易的.在Pastor－Satorras和 Vespingnani建立的无标度网络中的传染病传播模型就体现了这些特点[4～7].

由于解析方程建立的难度，所以上面的模型都不能将传染性与恢复性是按照一定概率进行的这个特点体现出来.同时没有考虑到网络中人与人之间的距离.

但是，计算机因为具有强大的计算功能，却可以将上述特点都体现出来.这样可以更直观的研究传染病的传播机理.

1 建立模型

首先，根据BA无标度网络的特点[3].随机产生网络图.

实际上，根据建立经典SIS模型时的条件[8].这里需要考虑传染病在单位时间内具有的两个重要特性:传播性(即与患病者的距离越近，则被传染的机率越大，但超过一定距离则不可能被传染)和恢复性(即患病者会按照一定的机率，变为健康者).

设Ai为网络中第i个人为健康者变为患病者;d为有效传播距离;d(i，j)为第i个人与第j个人的距离;Bi为患病者变为健康者;b为恢复率.

所以由传播性知，第i人由第j人传染成为患病者的机率为:

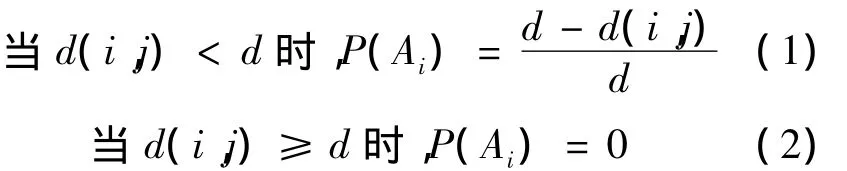
同时由恢复性知，第人由患病者变为健康者的机率为:

从模型中可看出传播性与有效传播距离和初始患病者的人数成正比，同时与恢复率成反比，下面在两种情况下模拟传染病的传播[2，8].

2 无标度网络下的SIS模型模拟

下面利用matlab编程，随机产生无标度网络图，在给定的初始患病人数，与有效接触距离和治愈率时的模拟结果.

当总人数为24939，初始患病人数为10，有效接触距离为2，治愈率为0.8时，下面图1至图10为每隔10个单位时间的网络蔓延图，图中灰色为正常人群，黑色为患病人群:

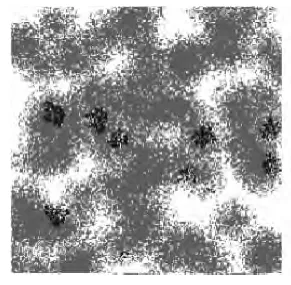
图1 t=10

图2 t=20

图3 t=30

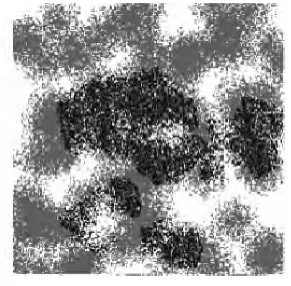
图4 t=40

图5 t=50

图6 t=60

图7 t=70

图8 t=80

图9 t=90

图10 t=100

所以，得到了这种情况对应的患病比例图:

而当总人数为24431，初始患病人数为5，有效接触距离为，治愈率为0.9.这时每隔十个单位时

间得到的疾病蔓延图12至图21为:

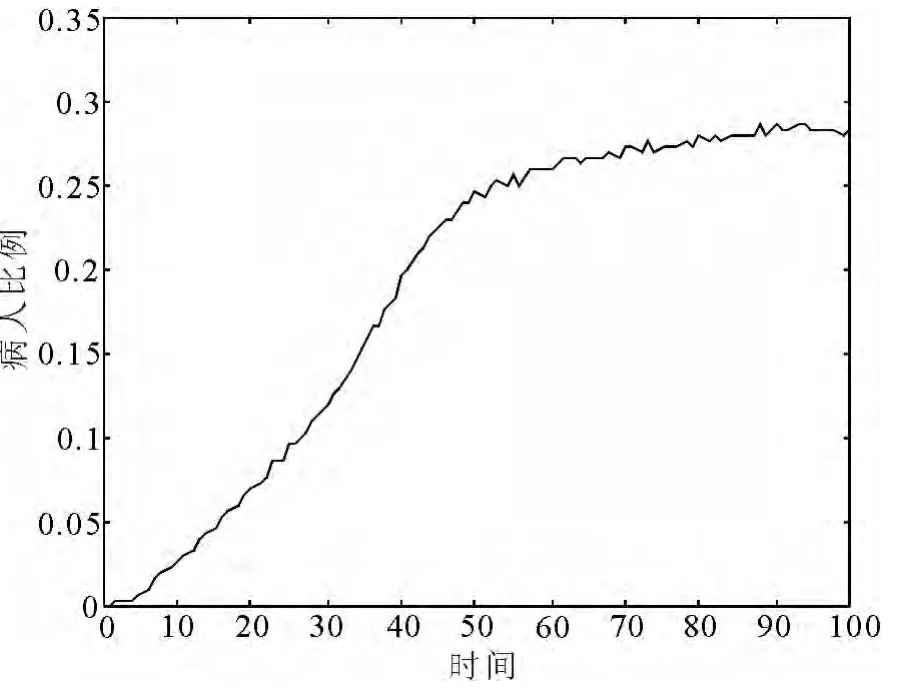
图11 病人随时间的比例图

图12 t=10

图13 t=20

图14 t=30

图15 t=40

图16 t=50

图17 t=60

图18 t=70

图19 t=80

图20 t=90

图21 t=100

所以，得到了第二种情况对应的患病比例图:

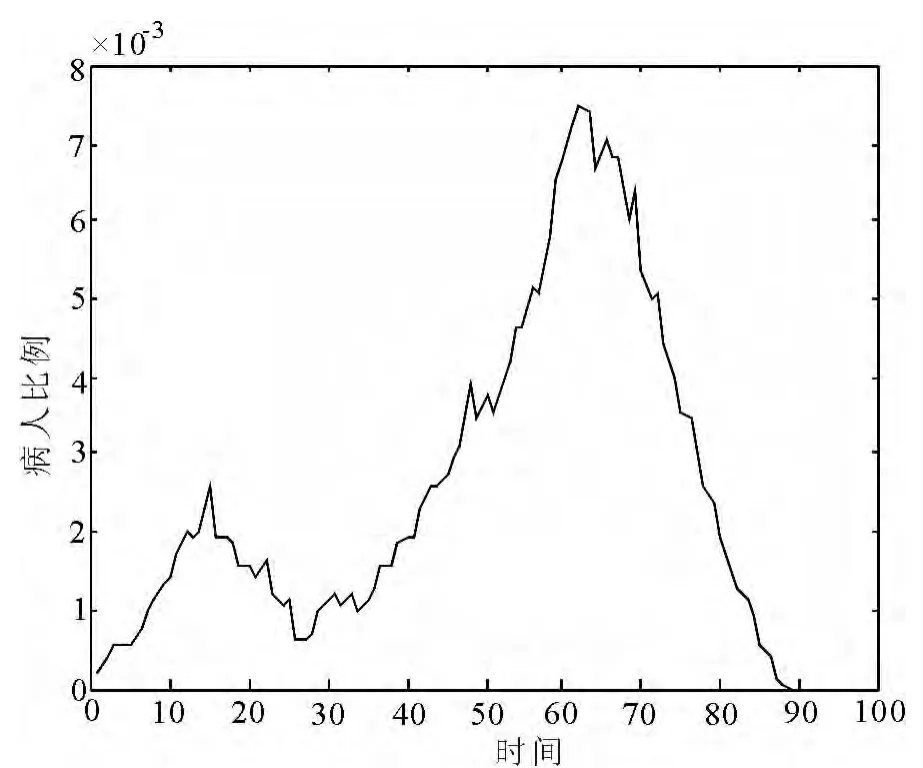
图22 病人随时间的比例图

通过上面两次实验，还不能直观的表现传播与初始患病人数和有效接触距离的关系，下面通过几组实验来具体分析传播规律，在实验里设定当患病人数达到总人数的1%，即认为传染病暴发.为了避免不同结构人群的分布不同，实验是在同一结构的人群里做的实验，人总数为:24896，由于一般的传染病都具有固定的治愈率，所以这里取治愈率为0.9.在实验数据中，0表示不传播，1表示传播:

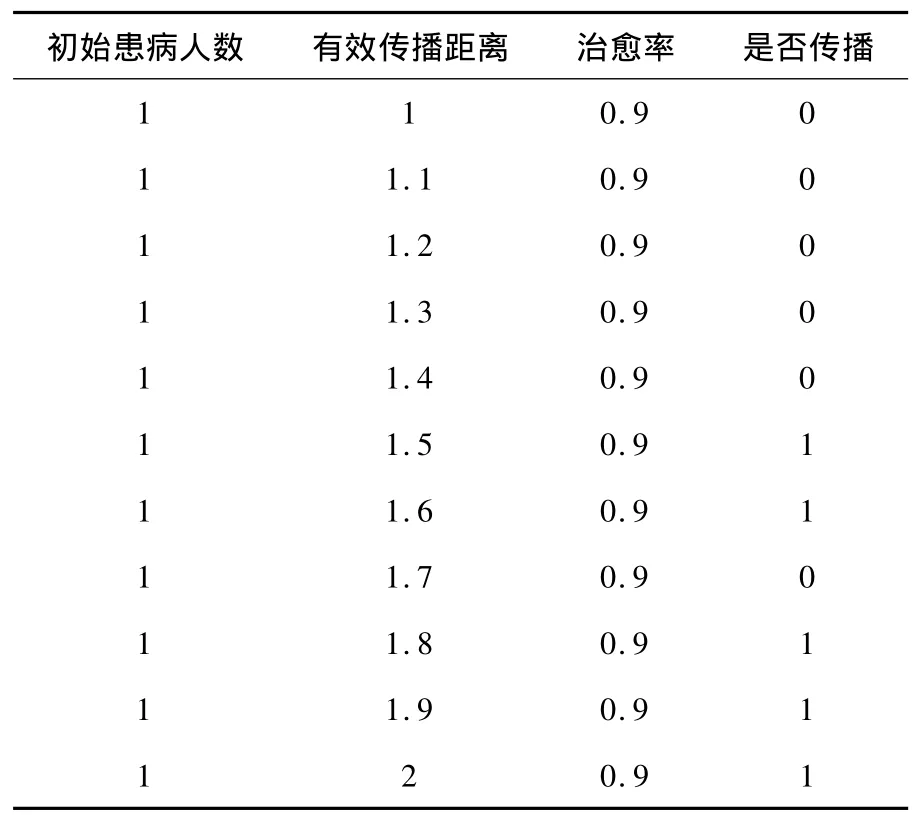
表1 第一组实验

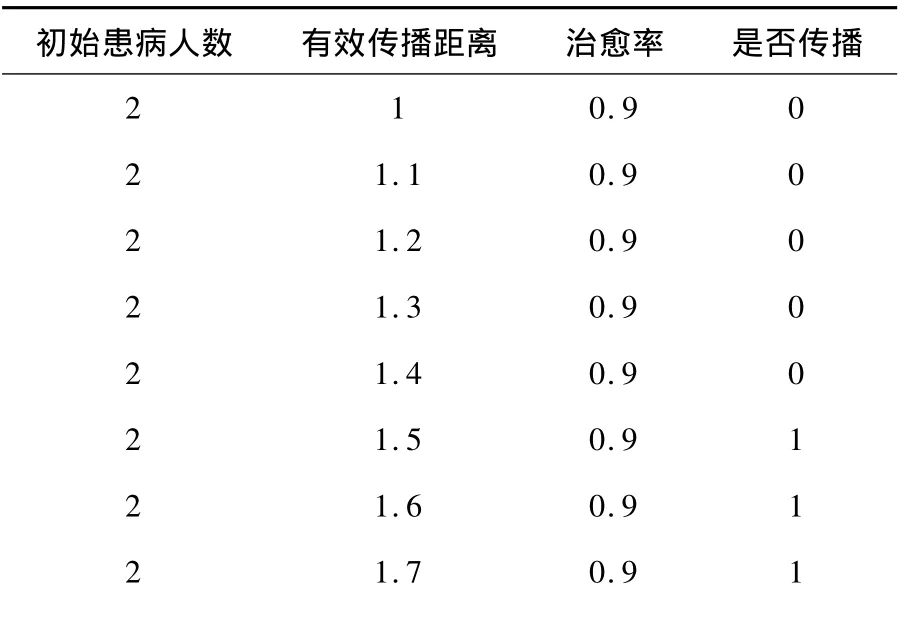
表2 第二组实验

2 1.8 0.9 1 2 1.9 0.9 1 2 2 0.9 1

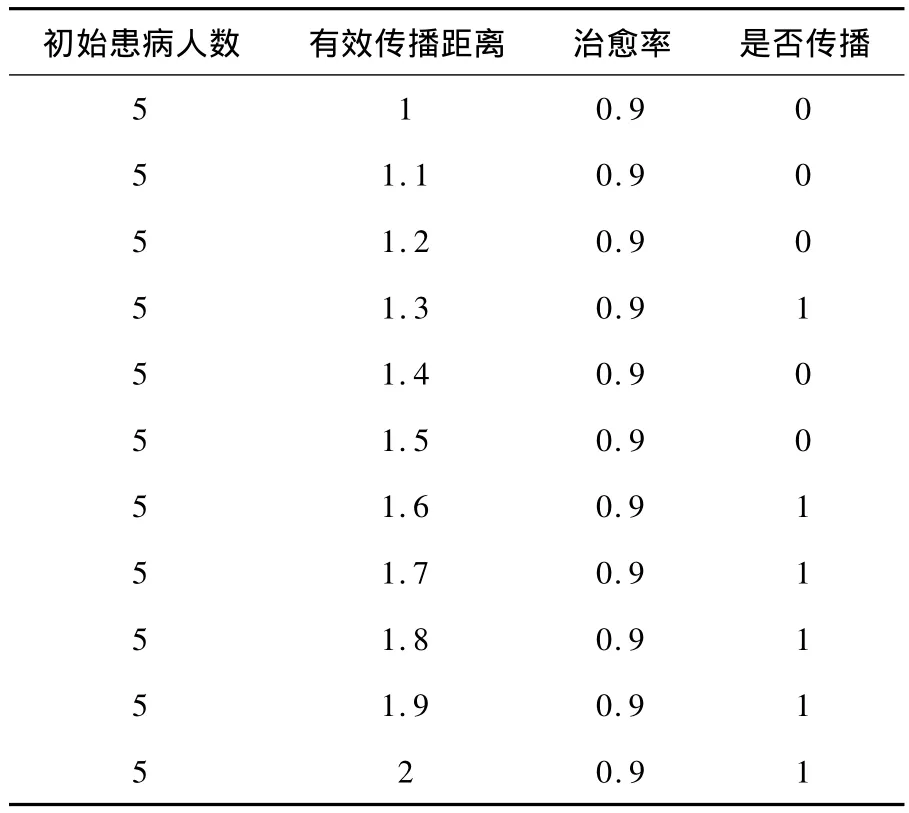
表3 第三组实验

图23 没有传播的初期图

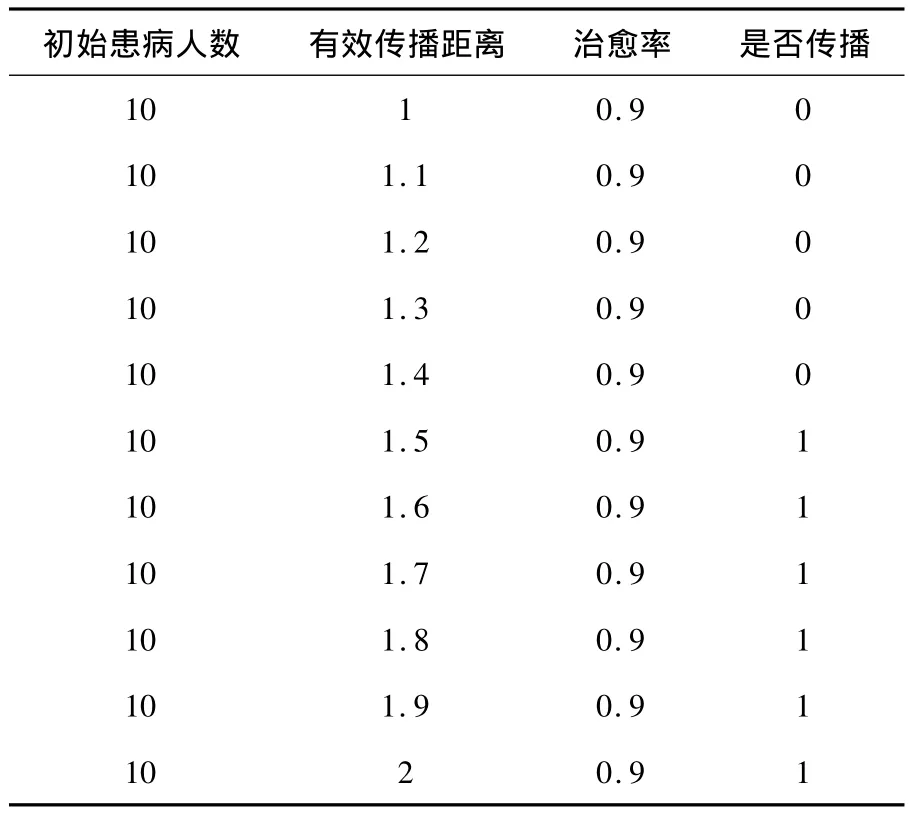
表4 第四组实验

通过上面四组实验，可以观察到，无标度网络下的传播有很强的敏感性，只要有患病者即有可能传播，而传染病的传播对初始患病人数没有很强的依赖，即只需有患病者即可，而对有效传播距离有很强的依赖性，这是在经典模型中看不到的.

所以只要传染病的传播能力比较强，即使初始患病者很少也能传播开，这也验证了，当年甲型流感的传播，最初传染源仅是个别从美洲回国的人员，竟然就能将疾病传播开来，说明传染病在无标度网络中是极易传播的，因为现代的航空网络即是无标度网络.

但同时也看到了在传播距离为1.3至1.7之间，是否传播是具有不稳定性的，所以通过下面一组实验来分析这种情况，下面实验是在同一结构的人群中，初始患病者为5人，有效传播距离1.5，治愈率0.9，的情况下，随机做了10次实验.

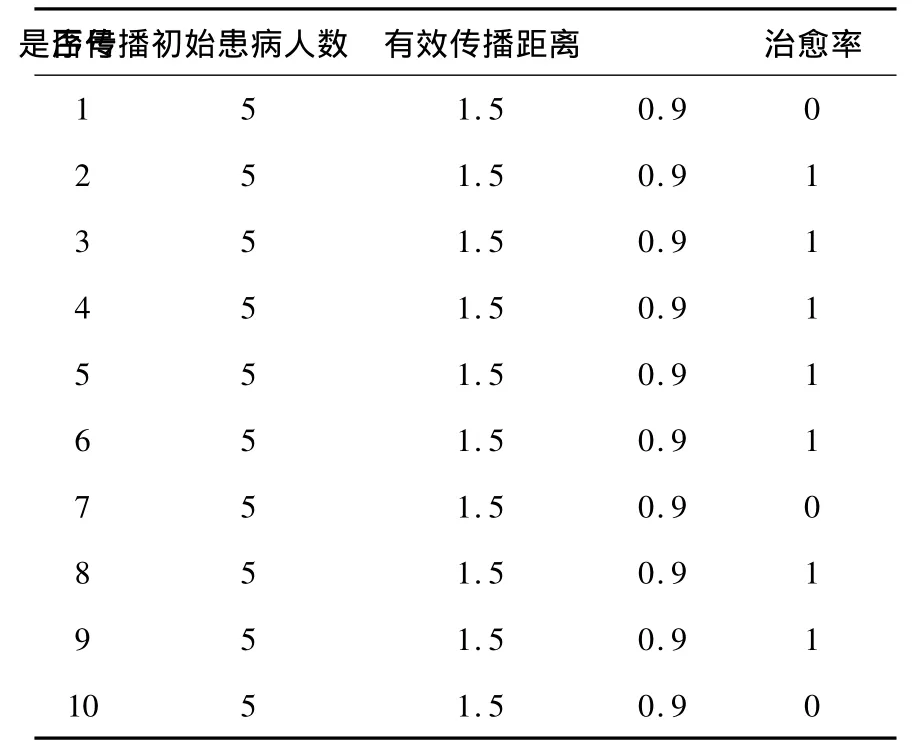
表5 第五组实验

从实验中可以看到即使在相同的数据下，也会出现不同的情况，这是什么原因呐?

图23是上面没有传播开的实验初期的传播图:

从图中的画圈处的病人可看出，若初期病人出现在密度较低处，则即使有效距离较大，也是不会传播的，但从概率的角度可知，若初始患病者越多，这种情况发生的可能性就越低，所以在第一组实验中，由于初始患病人数为1人，所以，这种不稳定就显得更强一些.

3 结论

从模拟结果可以知道，无标度网络对传染病传播的防范是非常脆弱的.只要有患病者出现，即就有可能传播开，而且传播对有效传播距离有很强的依赖性，也就是只要传染病够厉害，即使1人患病也照样传播，从实验中可以看到，有效传播距离的临界值应该是分布在1.3至1.7之间.这也验证了，前些年发生的甲型流感，最初传染源仅是个别从美洲回国的人员，竟然就能将疾病传播开来，说明传染病在无标度网络中是极易传播的.同时，计算机病毒传播也是典型的无标度网络传播，也是满足这种特性的.计算机模拟的好处就在于，可以利用事物直观的特性，建立比较简单的模型，来了解事物发展规律，结论比较直观.

[1]Watts D J，Strogatz S H.Collective Dynamics of‘Small－ World’Networks[J].Nature，1998，393(6684):440－442.

[2]汪小帆.复杂网络理论及其应用[M].北京:清华大学出版社，2006:73－78.

[3]Barrat A，Weigt M.On the Properties of Small World Networks[J].Eur.Phys.J.B，2000，13:547－560.

[4]Pastor－Satorras R，Vespingnani A.Epidemic Dynamics and Endemic States In Complex Networks[J].Phys.Rev.E，2001，63:066117.

[5]Pastor－ Satorras R，Vespingnani A.Epidemic Dynamics in Finite Size Scale－ Free Networks[J].Phys.Rev.E，2002，65:035108.

[6]Boguna M，Pastor－Satorras R.Epidemic Spreading in Correlated Complex Networks[J].Phys.Rev.E，2002，66:047104.

[7]Liu Z H，Lai Y C，Ye N.Propagation and Immunization of Infection on General Networks with both Homogeneous and Heterogeneous Components[J].Phys.Rev.E，2003，67:031911.

[8]姜启源.数学模型(第三版)[M].北京:高等教育出版社，2003:135－144.