全液压矫直机液压伺服非线性系统稳定性研究

王爱国

(太原重工技术中心，太原 030024)

矫直机在钢铁生产中是不可或缺的基础设备，广泛应用于钢板和钢管生产过程的矫直环节[1]，国外常用的矫直机液压系统都采用对称阀控非对称缸，他们为液压缸的有杆腔提供恒定背压来消除由于液压缸换向时所产生的巨大的压力和流量突变，但是这样就会使伺服阀长期在一侧工作，使得伺服阀的磨损加剧，寿命大大缩短了。为解决这一难题我们运用非对称阀控制非对称缸方法，但是对于矫直机液压伺服系统，液压缸在大行程运动时阀的开口大约都在50%～70%之间[2]，此时系统存在着大量的非线性和不确定因素，且四缸之间还存在一定的位置关系，是一类典型的大规模耦合非线性系统[3]。对于这种非线性系统，不能简单的进行线性化处理来判定其稳定性[4]，这样得出的结论会不符合实际情况，因此本文使用李亚普诺夫第二方法判定此系统的稳定性，这种方法是处理非线性系统稳定性问题强有力的一种方法[5]。

采用李亚普诺夫第二方法判断系统的稳定性，它不需要求出微分方程的解就可以确定系统的稳定性，大大减少了运算量，用李亚普诺夫第二方法判断系统稳定性时，最重要的就是李亚普诺夫函数的构建，李亚普诺夫函数的实质是一个虚构的能量函数，且这个函数是具有一阶偏导数的纯量函数[6]，李亚普诺夫定理认为只要此函数本身正定，一阶偏导数负定，则其在原点处的平衡状态是一致渐进稳定的，这就是李亚普诺夫定理的核心内容。

本文求解出非对称阀控非对称缸的状态方程，利用李亚普诺夫第二方法验证了此系统是稳定的。并运用AMEsim软件对矫直机的四缸同步性进行仿真，从同步性中分析了非对称阀控非对称缸的稳定性，最后通过现场的实际数据说明运用非对称阀控非对称缸的现实意义和必要性。

1 状态方程的建立

非对称阀控非对称缸的结构简图如图1.

△1，△2，△3，△4为阀芯各窗口的开口度，则各窗口的节流公式为：

图1 非对称阀控非对称缸结构简图Fig.1 Structure diagram of unsymmetrical cylinder withunsymmetrical valve control

则进出液压缸两腔的流量可表示为:

q1=f1(xv,p1)=qsv1-qsv4

(1)

q2=f2(xv,p2)=qsv3-qsv2

(2)

其中：Cd为流量系数；ω为阀口开口的面积梯度。

考虑液压油的可压缩性，液压缸内、外泄漏以及液压缸两腔液容的时变特性，并假设液压缸的内、外泄漏为层流流动，液压缸流量连续性方程可以表示为:

(3)

(4)

其中，V1(y)=A1(y0+y)+Vd1，

v2(y)=A2(L-y0-y)+Vd2,

qc=Cic(p1-p2),

Vd1，Vd2——无杆腔与有杆腔的死容积。

活塞的力平衡方程为(不计非线性摩擦力)：

(5)

根据前面介绍的基本方程(1)-(5)，可以建立非线性状态方程如下：

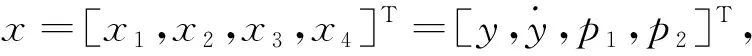
其中：f1(xv,p1)=q1=qsv1-qsv4

f2(xv,p2)=q2=qsv3-qsv2

2 系统稳定性的判定

以系统中的液体为研究对象，不考虑液体发热所产生的能量，根据液体的能量守恒构造Lyapunov函数：

其中：P1V1，P2V2分别为液压缸两腔液体的压能；

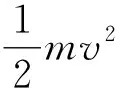
由于此式是能量守恒方程，因此必然正定。

(1)对V求一阶导，得：

(6)

∵x1>0，且K是个很大的系数(K是钢板的弹性模量)

同理，当x2<0，则x1<0，

(2)对于第3项

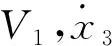
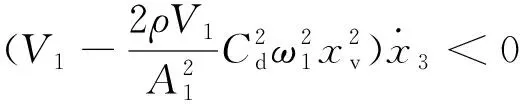
由于各个系数都大于0，所以第4项为负，所以式(6)负定，根据李雅普诺夫稳定性理论可知，此系统稳定。

3 系统的仿真研究

全液压矫直机中的四个压下缸都采用了非对称阀控非对称缸的方法，当压下时，四缸需同步，矫直机液压系统采用了跟随同步的方法。利用AMEsim软件建立系统模型如图2，为了能证明非对称阀控非对称缸的稳定性和在矫直机上的实用性，我们可以通过验证其同步性来说明非对称阀控非对称缸的稳定性。

液压缸考虑活塞两边容腔的压力动态，黏性阻力，活塞两边的泄漏，设活塞直径为640 mm，活塞杆直径为480 mm，行程为60 mm，设液压阀的固有频率为80 Hz，阻尼比为0.8，额定流量为200 L/min.

为了可以很清楚的分别四个缸的位移，设置每个缸的位移总比前一个缸的位移小5 mm，因此得到的曲线如图3，从图中可以很清楚的看出四个缸的同步性很好，稳定性也很好，没有出现任何波动，是完全可以满足工程的需要的。

4 实验研究

由太原科技大学设计，太原重工生产的全液压矫直机采用4WRDE16V200L高频响阀，其响应频率在控制信号的25%，幅值为-3 dB时的响应频率为100 Hz，液压缸总行程为300 mm，工作行程为260 mm，在现场工作的的实际情况和采集到的数据(如表1)可以看出，矫直机的四缸稳定性很好，浮动基本不超过0.03 mm，全液压矫直机中1#，4#缸同步，2#，3#缸同步[7]，现场设置1#，4#缸目标位置为24.5 mm，2#，3#缸目标位置为28.5 mm，从现场的数据可以看出，四缸的同步性很好，最大同步误差大约0.1 mm，并且四个缸距离目标位移最大误差约为0.2 mm，符合工程中的使用要求，并且比国外所采用的对称阀控非对称缸的系统位置控制效果好[8-10]，矫直出的钢板也满足国家标准。说明非对称阀控非对称缸在现场使用中是稳定和可行的。

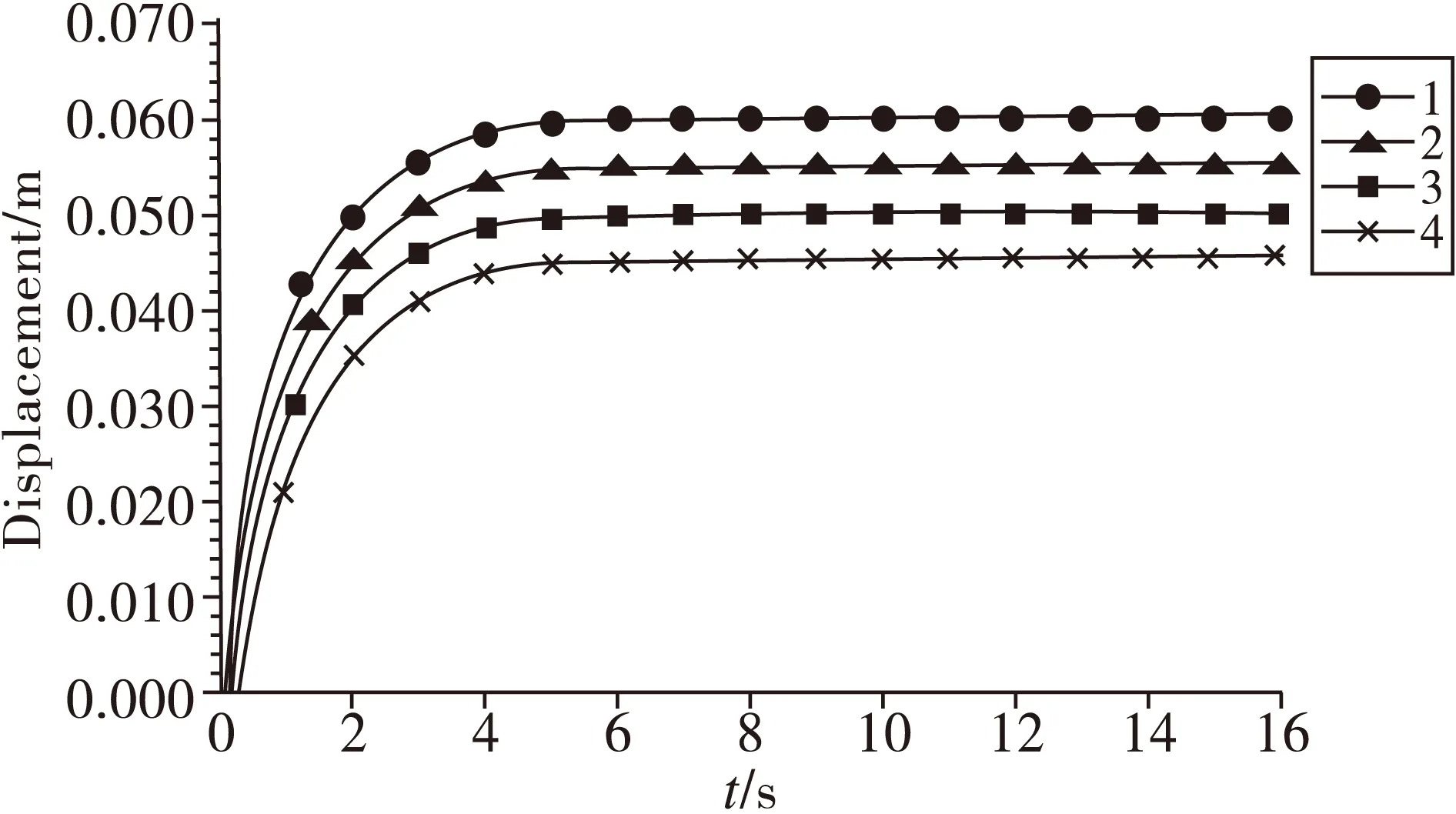
图3 液压缸的位移曲线Fig.3 Displacement curve of the cylinders

表1 现场采集数据Fig.4 Data of field sampling

5 结论

本文分析了全液压矫直机液压伺服系统中运用到的非对称阀控非对称缸的稳定性，由于伺服阀运行在非线性区域，不能用简单的线性化方法对其进行分析，所以本文运用李亚普诺夫第二方法证明了它的稳定性，这样即减小了运算量又使得状态方程中的一些重要量不会被忽略。然后利用AMEsim仿真软件对矫直机四个压下缸进行建模，通过验证其同步性来说明非对称阀控非对称缸的稳定性，最后从现场采集到的数据验证了此理论的可靠性和可行性。本文以液压矫直机为例严密地证明了非对称阀控非对称缸系统是稳定的，并且可以很好的减小液压缸换向带来的强大的压力和流量冲击，增大了元件的寿命。比国外常用的对称阀控非对称缸有更大的优势。非对称阀控非对称缸的应用在以后的工业发展中是一大趋势，尤其在负载变化较大、系统精度要求比较高的大型系统，一定会得到越来越多的应用[11]，非对称动力机构的液压伺服系统的高性能控制问题也应该引起越来越多的关注[12]。因此对于非对称阀控非对称缸的研究我们需要更加深入的研究和探索，充分发挥它的有效价值。

参考文献：

[1] WAIGAND A，DUNBAR A.Developments in roller leveling[J].Iron and Steel Technology Conference Proceeding，2004，2：335-344.

[2] 王传礼，丁凡，李其鹏，等.对称四通阀控非对称液压缸伺服系统动态特性研究[J].中国机械工程，2004，16：471-473.

[3] 关景泰，王海滨，周俊龙.非对称阀控制非对称缸的动态特性[J].同济大学学报，2001，29(9)：1130-1134.

[4] YAO B，BU F，REEDY J.Adaptive robust motion control of single-rod hydraulic actuators：theory and experiments[J].IEEE/ASME Transactions on Mechatronics，2000，5(1)：79-91.

[5] BO GUO，YUGUI LI，HEYONG HAN.Analysis of Asymmetric Valve Control Asymmetric Cylinder System of Hydraulic Leveler[J].Advances in Rolling Equipment and Technologies，2011，145：477-480.

[6] 杨军宏，李圣怡，戴一帆.阀控非对称缸系统的稳定性分析与设计[J].机械科学与技术，2007，26(12)：1625-1629.

[7] 刘公平.李亚普诺夫第二法主稳定性定理的证明与应用[J].山东轻工业大学学报，1991(1)：42-51

[8] 张嗣瀛，高立群.现代控制理论[M].北京：清华大学出版社，2006.

[9] 王栋梁，李洪人，张景春.非对称阀控制非对称缸的分析研究[J].济南大学学报，2003，17(2)：118-123.

[10] 王春行.液压控制系统[M].北京：机械工业出版社，2003.

[11] 郭波.液压矫直机阀控缸系统研究[D].太原：太原科技大学，2011.