柔性支承下风力机系统建模及轴承振动分析

那亚莉，殷玉枫，丁健刚，王洪涛

(太原科技大学机械工程学院，太原 030024)

风能发电由于清洁无污染、成本较低，取用不尽等优点，有效缓解了能源污染、雾霾和全球变暖等问题，并且在可再生能源开发中技术相对成熟，极具开发前景。随着风力机大型化，对风力机传动系统可靠性提出了更高的要求，风力机设计理论方面的不足渐渐显现，现有的研究成果已无法直接用于载荷情况极端、支承结构柔性大的风力机上，风力机实际使用寿命远低于其设计寿命。

长期以来，国内外学者对滚动轴承振动特性做了大量研究。Lundberg等[1]通过静力学分析了滚动体的变形，但没有考虑惯性力、摩擦力等的影响；Jones[2]考虑了离心力及陀螺力矩的影响，建立滚动轴承拟静力学模型。郑林庆[3]建立滚动轴承拟动力学模型，通过弹流润滑理论，对接触区因摩擦产生的热效应进行分析。

齿轮箱是故障率最高的部件之一，其中齿轮箱轴承失效率居于首位。由于风力机轴承特殊的工作环境、所受载荷的时变性，使得轴承设计分析变得相当复杂。本文建立了极端载荷下基于柔性支承的风力机传动系统耦合动力学模型，讨论打滑区域摩擦力、内圈转速等激励对轴承振动特性的影响，为风力机轴承设计提供了一定的理论指导。

1 柔性支承下风力机传动系统动力学分析

风力机传动系统在高空极端载荷环境下运行，随着风力机单机功率的不断增加，塔架高度增加，柔性增大。

1.1 柔性支承下风力机传动系统动力学模型

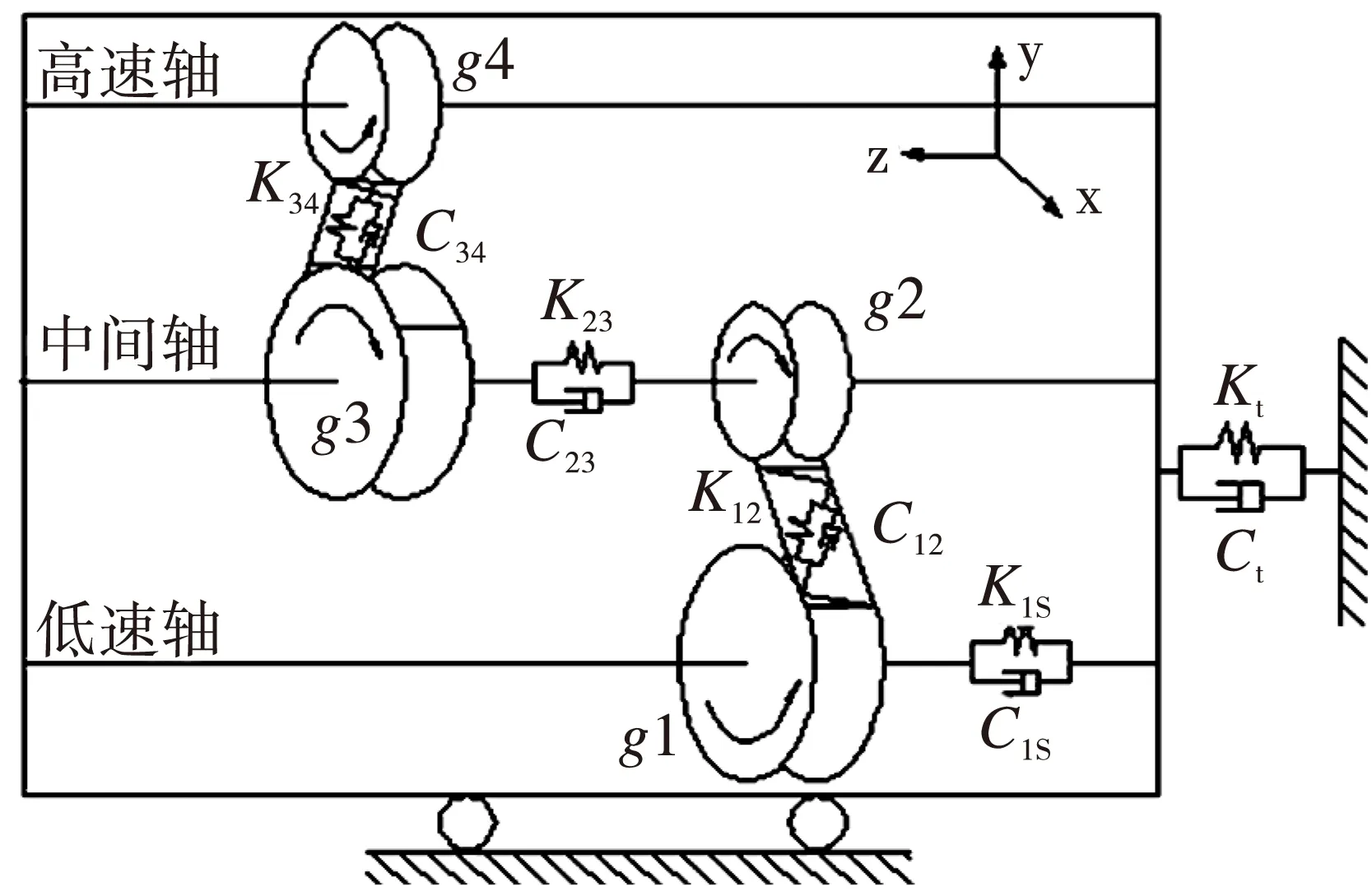
图1 二级斜齿轮传动耦合示意图Fig.1 Coupled model of two-stage helical gear

目前，风力机传动系统普遍采用一级行星齿轮加二级斜齿轮的形式。塔架在随机风载荷的作用下产生柔性变形，使得齿轮箱二级斜齿轮传动系统产生轴向的耦合运动，其耦合示意图如图1.其中gi(i=1，2，3，4)为对应斜齿轮；K1s，C1s分别为低速轴扭转刚度、阻尼；K23，C23分别为中速轴扭转刚度、阻尼；K12，C12分别为斜齿轮g1与g2间时变啮合刚度、粘性阻尼；K34，C34分别为斜齿轮g3与g4间时变啮合刚度、粘性阻尼；Kt，Ct分别为塔架支承刚度、阻尼。

根据拉格朗日方程推导出二级斜齿轮传动系统耦合动力学方程，如式(1).

Kz1z1=0

Kz3(zM3+z3)=0

(1)

式(1)中：Ii(i=1，2，3，4)分别为斜齿轮gi的转动惯量；mi(i=1，2，3，4)分别为斜齿轮gi的质量；Mi(i=1，2，3，4)为齿轮箱(除去mi)的质量；rbi(i=1，2，3，4)分别为斜齿轮gi的基圆半径；Kzi，Czi(i=1，2，3，4)分别为齿轮箱(除去mi)的支承刚度、阻尼，Tinx、Tout分别为齿轮箱输入扭矩、输出扭矩。

2 滚动轴承动载荷计算

2.1 滚动轴承动载荷

滚动轴承在外部和内部激励的共同作用下产生复杂动载荷，这是轴承设计所需要的重要数据之一。滚动轴承动载荷定义为振动方向位移与轴承刚度的乘积，当解得系统各自由度的位移解后，可以由此计算出动载荷，其计算公式为：

Fgi=Kgixi

(2)

式(2)中：Fgi为滚动轴承径向或者轴向载荷；Kgi为滚动轴承径向或者轴向刚度；xi径向或者轴向位移。

2.2 滚动轴承载荷系数

考虑到风力机实际工作环境中冲击力、不平衡作用力等难以精确计算的附加载荷，需要在当量动载荷的基础上乘以一个载荷系数。常规的设计方法为经验法，通过查表获得，本文由动力学分析计算得出，依据公式(2)得到轴承径向和轴向动载荷，则轴承载荷系数的计算公式为：

fp=(P+Fgp)/P

(3)

式(3)中：P为当量动载荷，P=XFr+YFa；X,Y为径向和轴向折算系数，由手册查得；Fr,Fa为径向动载荷和轴向动载荷；Fgp为由激励引起的当量动载荷，Fgp=XFgr+YFga；Fgr,Fga为激励产生的径向载荷和轴向载荷。

3 风力机二级斜齿轮轴承摩擦振动方程建立

3.1 摩擦振动模型

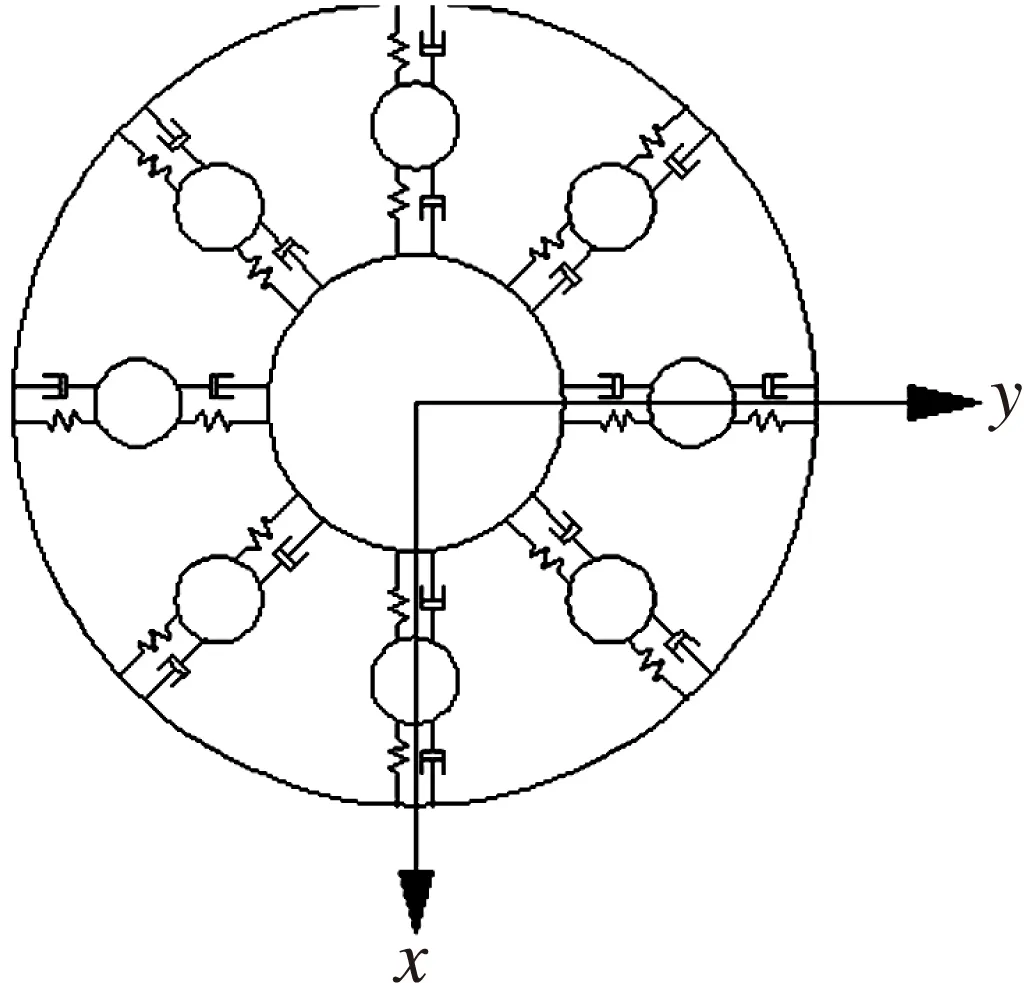
图2 轴承振动模型Fig.2 Vibration model of bearing

基于纯滚动理论建立轴承振动模型[1]，其物理模型简化为弹簧阻尼系统，如图2所示，模型中考虑了x和y两个方向的自由度。

3.2 摩擦振动方程

在打滑区域将摩擦力引入纯滚动振动模型，那么摩擦力的大小表示为：

F=μKnδ1.5

(4)

式(4)中：μ为滑动摩擦系数；δ为接触变形；Kn轴承等效刚度。

那么摩擦力在X、Y方向的合力分别表示为：

Fux=-μKn(xcosθl+ysinθl-e)1.5sinθj

(5)

Fuy=μKn(xcosθl+ysinθl-e)1.5cosθj

(6)

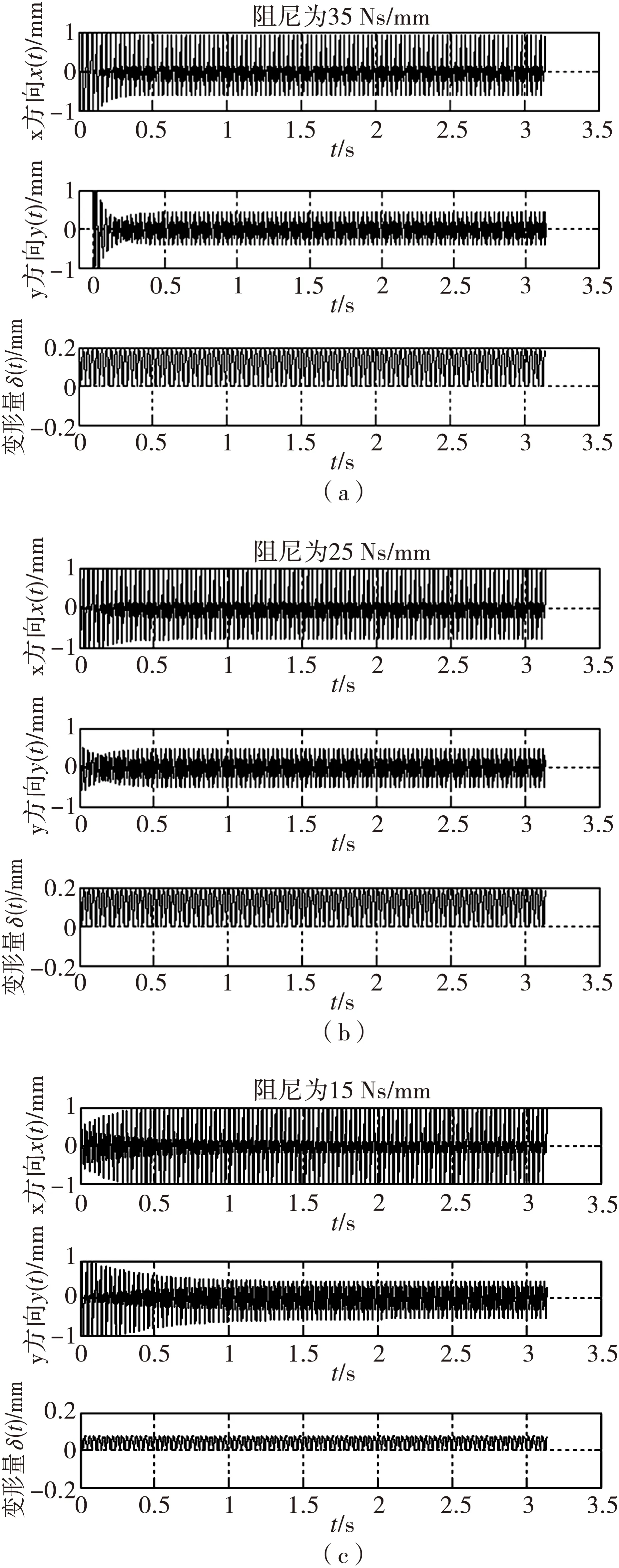
图3 不同阻尼下轴承振动特性分析Fig.3 The vibration analysis under different damping

其运动微分方程表示为：

(7)

(8)

式(7)中：mi为内圈质量，W为轴承所受径向载荷。

4 风力机二级斜齿轮传动系统摩擦振动分析

在本节中，仿真了风力机齿轮箱轴承在极端工作环境下的动态响应，其极端工作载荷由参数化概率拟合模型得出。系统参数如表1.

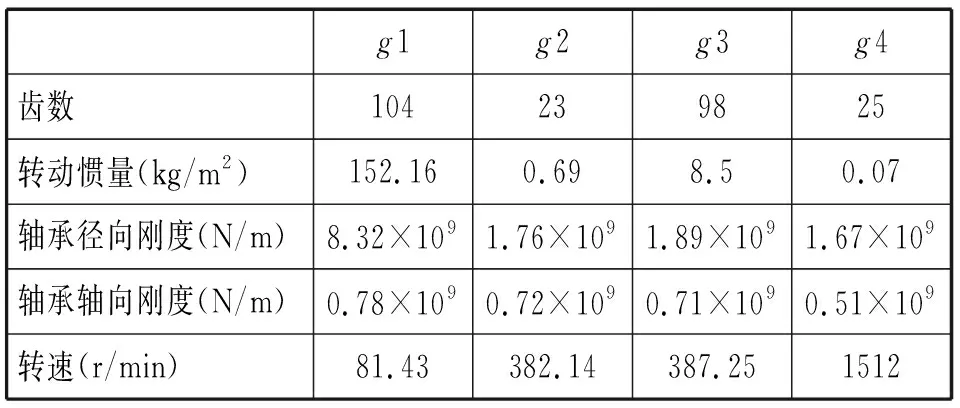
表1 系统参数Tab.1 Parameters of system

4.1 不同阻尼对振动特性的影响

因为轴承振动响应引入了摩擦激励，这里着重分析阻尼对振动特性的影响。阻尼不是轴承结构参数，但阻尼对轴承的振动有很大的影响。阻尼的计算非常困难，在建立的摩擦振动模型中，等效粘性阻尼与轴承振动直接相关，这里只给出经验计算值，下面分别取粘性阻尼35 Ns/mm、25 Ns/mm、15 Ns/mm进行对比分析，结果如图3.

分析图3可知，不同阻尼下打滑区域振动是不同的，阻尼为25 Ns/mm时振动幅度不是特别大，这是由于轴承刚进入承载区所受摩擦力不同而造成的。在y方向上的位移可以看出，阻尼过大或者过小使得轴承在刚开始进入承载区时打滑振动非常大，然后渐渐趋于平稳。当阻尼为15 Ns/mm时，轴承的振动位移偏大，这种现象说明阻尼的选取应该在合理的范围内，根据特定的条件进行选择，这样也可以避免出现共振现象。

4.2 不同轴承转速对振动特性的影响

本节分别分析了500 r/min、1 000 r/min、1 500 r/min这三组转速下轴承的振动特性。在相同的响应时间内，不同转速下轴承各方向振动响应如图4所示。

由图4可得：在内圈转速较低的情况下滚动体在打滑时引起的振动比较微弱，分布较散，高速情况下的振动情况则相反。这主要是由于高转速情况下，打滑区域的范围增大的原因造成的。随着转速的提高，其在x和y方向上的位移逐步增大，转速对轴承的振动特性有着很大的影响。

5 结论

建立了柔性支承下风力机传动系统动力学模型及摩擦振动模型，考虑打滑区域阻尼、轴承转速等因素，对比分析了极端载荷下轴承振动特性，得出结论如下：

(1)阻尼在35 Ns/mm或15 Ns/mm时轴承在y方向上振动位移非常大，然后渐渐趋于平稳。这种现象说明润滑阻尼对y方向上振动影响较大，并且阻尼的选取应该在合理的范围内，根据特定的条件进行选择，这样也可以避免出现共振现象。

(2)分析对比了500 r/min、1 000 r/min、1 500 r/min这三组转速下轴承的振动特性，转速对轴承的振动特性有着很大的影响。在相同的响应时间内，内圈转速较低的情况下滚动体在打滑时引起的振动比较微弱，分布较散，高速情况下的振动情况则相反。

参考文献：

[1] LUNDBERG G，PALMGREN A.Dynamic capacity of rolling bearings[J].Mechanical Engineering Series，1947，1(3)：5-50.

[2] JONES A B.A genal theory for elastically constrained ball and radial roller bearings under arbitrary load and speed conditions[J].Journal of Basic Engeering Transaction of the ASME，1960，8(2)：309-320.

[3] 郑林庆，朱东.高速滚子轴承的打滑分析[J].润滑与密封，1982(4)：79-84.

[4] 唐云冰，高德平，罗贵火.滚动轴承非线性轴承力及其轴承系统振动特性的影响.航空动力学报[J]，2006，21(2)：366-373.

[5] 李锦标，吴林丰.高速滚子轴承的动力学分析[J].航空学报，1992，13(12)：625-632.

[6] 黎明安.MATLAB/Simulink动力学系统建模与仿真[M].北京：国防工业出版社，2012.

[7] 薛小倩.风速模拟与风力机风轮模拟的研究[D].内蒙古包头：内蒙古科技大学，2012.

[8] 王建军，李润方.齿轮系统非线性振动研究发展[J].力学进展，2005，35(1)：37-51.

[9] 王峰，陈棋，余国城.大型风力发电机组塔架刚度的研究[J].新能源及工艺，2005(5)：38-40.

[10] 刘家文.滚动轴承设计与应用手册[M].武汉：华中工学院出版社，1985.