利用微分求积法分析静态圆柱板

高文安，王居林 (山西建筑职业技术学院，太原 030006)

复合材料圆柱板由于具有易成型、低密度的特点，被广泛用于大量工程中。一般来说，使用三维弹性方程分析这种结构会设计到大量的数学问题。简单边界条件的圆柱板已得到详细的分析，Ren J G等求出了圆柱板在两对边简支条件下的解析解[1-2]，Varadan T K、Huang N N、Chan-drashekhara K等利用试验的方法验证了Ren J G的解析解[3-7]。但在实际工程中简单边界条件的圆柱板应用较少，相比较而言，复杂边界条件的圆柱板得到广泛的使用，而在文献中还没有相关的文章。基于此，本文结合微分求积法和傅立叶级数分析圆柱板在不同边界条件下的力学行为，最后通过数值计算验证了该方法的可行性和有效性。

2 圆柱板本构方程的建立

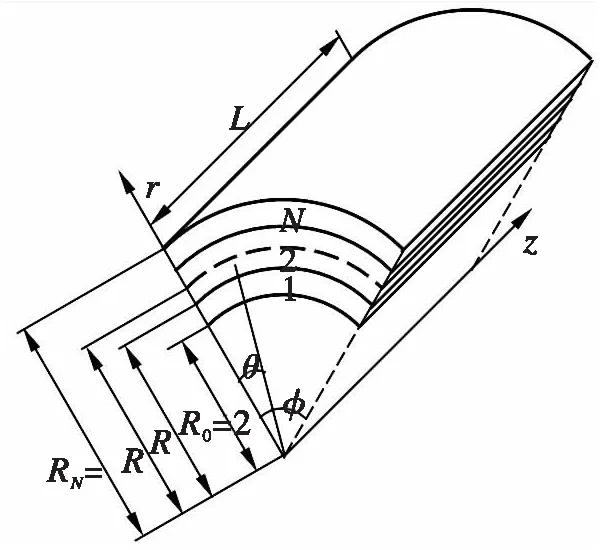
图1 圆柱板及其r，θ，z坐标轴

分析一有M层的圆柱板，如图1所示，每层为均匀的正交各向异性材料，任意一层在参考坐标系(r,θ,z)中的本构方程为：

(1)

其中，σij，εij分别是应力应变向量，Cij是材料弹性系数。在不考虑自重时，板的控制方程为：

(2)

其中，ur，uθ和uz分别表示在r，θ和z方向上的位移；ρ表示板的密度。其应变和位移的关系为：

(3)

板上下表面不受约束，因此有：

σr=qτzr=τrθ=0

(4a)

σr=τzr=τrθ=0

(4b)

假定板一对边为简支，该对边的位置分别为θ=0，θ=θm，则有：

(5)

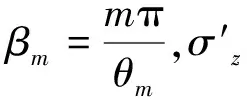
(6)

dδ/dη=Gδ

(7)

其中，δ和G分别表示状态变量矩阵和常系数矩阵[9]。

式(5)的状态变量有下述表达式：

(8)

为了得到板的问题解，对公式(5)的状态变量进一步作以下假定：

(9)

(10)

对公式(10)积分得：

(11)

当η=ηk，上式可得：

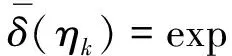
(12)

(13)

把公式(12)代入到公式(13)得：

(14)

对所有M层进行类似公式(12)，公式(13)和公式(14)的分析得：

(15)

其中，S=πexp[Gkhk]是全局转换矩阵。把公式(4)代入到公式(12)得：

[Sij]{δj}={q0 0}T(i=1,5,6;j=2,3,4)

(16)

从公式(16)能解得位移矩阵{δj}，把{δj}和公式(4b)代入到公式(11)，联立公式(8)和公式(11)并求解，最后得到圆柱板的应力。

(17)

其中，N表示分析点的数量，gij表示加权系数。把公式(17)应用到公式(7)中，能得到状态方程在分析点xj的状态变量：

(18)

同理，可以得到公式(8)中的变量：

(19)

(20)

(21)

应用边界条件z=0,L，可以求解公式(20)得到状态变量θk.当边界条件z=0,L时，作如下假定：

(22)

(23)

其中，下标b表示状态方程考虑了边界条件。同理，公式(15)考虑到边界条件可得：

△b(h)=Tb△b(0)

(24)

其中，Tb=πexp[Mbhk]是全局转换矩阵。把公式(4)代入到公式(24)得：

[Tij]{△j}={q0 0}T(i=1,5,6;j=2,3,4)

(25)

2 数值计算与分析

现分析计算一个三维圆柱板，其坐标系为：

板的每层厚度相同，物理属性为：

为了计算的准确性和收敛性，圆柱板的每层又划分成若干层。从图2可以看出，每一层细划分至15层时，该方法分析的横截面剪应力接近精确解。图2-图6显示正应力，横截面剪应力和沿圆周正应力的计算结果分析图，与实验结果较为吻合[11-16]。从以上的分析可以看出：该方法能够准确地求解圆柱板在复杂边界条件下的应力和应变。

图2 横截面尺寸S=10，θ=0，z=L/2时的剪应力

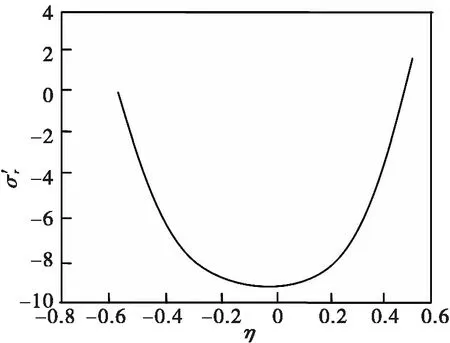
图3 横截面尺寸S=50，θ=0，z=L/2时的正应力

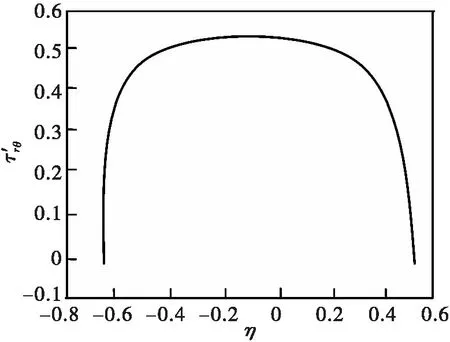
图4 横截面尺寸S=50，θ=0，z=L/2时的剪应力

图5 横截面尺寸S=50，θ=0，z=L/2时的沿圆周正应力

3 结论

微分求积法用于对圆柱板在一对边简支约束而另一对边任意约束情况下的静态分析，克服了传统的空间状态法不易求解非简单边界条件。通过对一个圆柱板的数值分析，表明该方法能准确地分析圆柱板在不同边界条件下的力学行为。

参考文献：

[1] REN J G.Exact solutions for laminated cylindrical shells in cylindrical bending[J].Compos Sci Technol，2007，29：167-187.

[2] REN J G.Analysis of simply supported laminated circular cylindrical shell roofs[J].Compos Struct，2008，11：277-292.

[3] VARADAN T K，BHASKAR K.Bending of laminated orthotropic cylindrical shells-anelasticity approach[J].Compos Struct，2011，17(2)：141-156.

[4] HUANG N N，TAUCHERT T R.Thermoelastic solution for cross-ply cylindrical panels[J].Therm Stress，2011，14：227-237.

[5] HUANG N N，TAUCHERT T R.Thermal stresses in doubly-curved cross-ply laminates[J].Solids Structures，2012，29：991-1000.

[6] CHANDRASHEKHARA K，KUMAR B S.Static analysis of thick laminated circular cylindrical shells[J].Pressure Vessel Technol，2013，115：193-200.

[7] BHASKAR K，VARADAN T K.Benchmark elasticity solution for locally loaded laminated orthotropic cylindrical shells[J].AIAA，3013，32(3)：627-632.

[8] HUNG-SYING J，KUAN-GOANG T.Elasticity solution for laminated anisotropic cylindrical panels in cylindrical bending[J].Compos Struct，2012，30：307-317.

[9] BHASKAR K，GANAPATHYSARAN N.Elasticity solution for laminated orthotropic cylindrical shells subjected to localized longitudinal and circumferential moments[J].Pressure Vessel Technol，2013，125：26-35.

[10] 钱纯，杨嘉陵.复合材料层合板的非线形动力稳定性[J].航空学报，1996，17(S1)：95-98.

[11] BERT C W，JANG S K，STRIZ A G.Nonlinear bending analysis of orthotropic rectangular plates by the method of differential quadrature[J].Comput Mech，2011，5：217-226.

[12] CHEN W Q，LV C F，BIAN Z G.Elasticity solution for free vibration of laminated beams[J].Compos Struct，2013，62：75-82.

[13] CHEN W Q，LV C F.3D free vibration analysis of cross-ply laminated plates with one pair of opposite edges simply supported[J].Compos Struct，2011，69：77-87.

[14] 聂国隽，仲正.微分求积单元法在结构工程中的应用[J].力学季刊，2005，23：35-39.

[15] HUNG-SYING J，KUAN-GOANG T.Approximate elasticity solution for laminated anisotropic finite cylinders[J].AIAA，2013，3(11)：2121-2129.

[16] SHU C，RICHARDS B E.Application of generalized differential quadrature to solve two-dimensional incompressible Navier-Stokes equations[J].Numer Methods Fluids，2012，15：791-798.