应用角动量升降算符分析角动量的矩阵表示和表象变换

田杏霞，王 鹏，王 艳

(通化师范学院 物理学院，吉林 通化 134002)

在量子力学中，算符和波函数的具体表示形式由选择的表象决定．同一个算符在两个不同表象之间的表示可以通过变换矩阵换算，但在角动量问题中，角动量分量的矩阵表示并不容易求得，本文利用升降算符计算角动量的矩阵表示，以及不同分量表象之间的变换[1-2]．

1 角动量升降算符

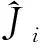
(1)

(2)

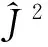
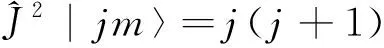
(3)

(4)

1.1 升降算符的定义

定义算符

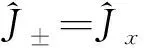
(5)

升降算符与角动量分量满足如下关系：

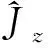
(6a)

(6b)

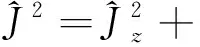
(6c)

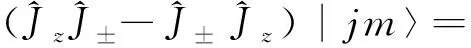
(7)

1.2 升降算符对波函数的作用

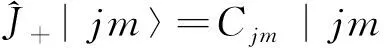
(8)

(9)

将(9)式左作用于(8)式，我们可以得到：

(10)

将(6c)式代入上式的左边进行整理，得到：

与(10)式对比，得：

|Cjm|2〈jm+1|jm+1〉=
(j(j+1)ћ2-m2ћ2-mћ2)〈jm|jm〉

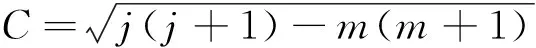
所以升降算符对波函数|jm〉的作用：

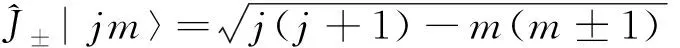
(11)

2 利用升降算符建立表象的变换矩阵

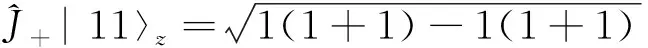
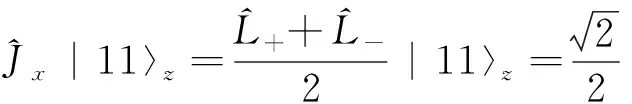
(12a)

(12b)

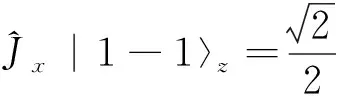
(12c)

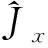
(13)

(14)

|1m〉x=c1|11〉+c2|10〉+c3|1-1〉

(15)

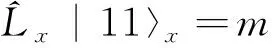
同理可得：

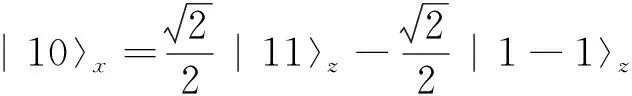
根据表象变换矩阵元的定义[1,2]，我们可以得到从z表象到x表象的变换矩阵为：

(16)

按照同样的方法可以知道从z表象变到y表象的变换矩阵为：

(17)

3 总结

求解角动量算符的矩阵表示和

分量表象之间的变换矩阵的方法有很多，每一种方法都有自己的优点和缺点．本文通过引入升降算符，用简单的计算给出了角动量分量算符在z表象中的表示，同时推导了从z表象到x(y)表象的变换矩阵．在文中以j=1为例，这一方法可以推广j为任何值的情况．

参考文献：

[1]周世勋.量子力学教程[M].北京:人民教育出版社，2009：94-117.

[2]曾谨言.量子力学[M].北京:科学出版社，2007:251-256.

[3]马宇晓.量子数l的上升算符和下降算符对|l，m〉的作用[J].大学物理，2002(09).