计算电磁学及其在复杂电磁环境数值模拟中的应用和发展趋势

周海京， 刘 阳， 李瀚宇， 董 烨，廖 成， 董志伟， 莫则尧

计算电磁学及其在复杂电磁环境数值模拟中的应用和发展趋势

周海京1，2， 刘 阳1，2， 李瀚宇1，2， 董 烨1，2，廖 成3， 董志伟1，2， 莫则尧1，2

（1.北京应用物理与计算数学研究所，北京 100094；2.中物院高性能数值模拟软件中心，北京 100088；3.西南交通大学电磁所，成都 610031）

概述计算电磁学的发展历程及其数值方法，并从学术研究、商业软件以及专用软件三个层次论述国内外研究的最新进展.结合复杂电磁环境的应用介绍复杂电磁环境数值模拟平台的研究现状，最后提出未来发展趋势的几点设想.

计算电磁学；复杂电磁环境；高性能计算

0 概述

0.1 计算电磁学

从研究手段（或研究途径）的角度考察，我们发现，电磁学的发展历程大致可以分为实验电磁学（1864年以前），经典电磁学（1864年－1950年代）和计算电磁学（1950年代至今）三个阶段.实验电磁学是建立在来自实验的感性认识基础上的，这一阶段的标志性工作包括库伦、安培以及法拉第等实验定律.1864年，苏格兰物理学家麦克斯韦在上述实验定律的基础上建立了麦克斯韦方程，揭示了自然界一切宏观电磁现象所遵循的普遍规律，使电磁学真正上升为一门理论，也标志着电磁学迈入经典电磁学的发展阶段.电子计算机发明之前，人们通过应用经典电磁理论求解具有规则边界简单问题（如球、圆柱、平面等）的解析解，获得电磁场问题的物理或工程上的解释或认知.这种方法效率高且可得到问题的准确解，如分离变量法、格林函数法、保角变换等，但适用范围太窄.为求解较复杂的电磁场问题，人们发展了渐进方法，如高频近似方法等.然而，面对工程电磁问题中越来越复杂的边界条件时，解析或渐进方法往往无能为力.20世纪50年代以来，电子计算机技术飞速发展，计算机强大的计算能力使其取代了只依赖纸和笔的传统计算模式，成为科学和工程技术发展中不可或缺的计算分析工具.在计算机辅助下，电磁场数值计算方法能够求解形状复杂不规则的实际问题，其解在一定程度上满足了实际应用的精度.随着电磁场数值计算方法在实际工程问题中的广泛应用，计算电磁学研究领域已成为现代电磁理论研究的主流［1］.概括来讲，计算电磁学是以电磁场理论为基础，以数值计算技术为手段，运用计算数学提供的各种数值方法，解决复杂电磁场理论和工程问题，是目前电磁场与微波技术学科中十分活跃的一个研究领域.

0.2 计算电磁学数值方法

目前，计算电磁学方法从名称上来分种类繁多，曾经有学者试图在现有算法基础上总结出计算电磁学族谱，其中列出有正式名称的算法就多达五十种之多.限于篇幅，本文只作概念性分类描述.从求解麦克斯韦方程的方法来分，可分为解析法、渐进法和数值法三类.解析法是指严格求解麦克斯韦方程的方法，通常只适用于理想的边界条件，如分离变量法只能在十一种可以作变量分离的坐标系下进行求解.渐进法是指在极限条件下求解麦克斯韦方程的近似形式，如低频近似下退化为准静态问题和电路问题，高频近似下的光学和准光学方法，包括几何光学法、物理光学法、几何／物理／一致绕射方法、高斯波束法等［2－5］.而大部分计算电磁学方法则被归于数值方法，即用离散化方法通过计算机程序直接求得麦克斯韦方程及其衍生方程的数值解［6］.

在电磁学领域中，目标体的特征尺寸与波长之比是一个重要参数，即目标体的电尺寸.通常可以根据目标体的电尺寸大小将问题分为低频、中频和高频问题［7］.当目标体的特征尺寸远小于波长时，该问题属于低频问题，电路物理占据主导地位，可利用静态场或准静态场近似建立模型提高计算效率；当目标体的特征尺寸远大于波长时，该问题属于高频问题，射线物理占据主导地位，高频渐近方法适用于该类问题；当目标体的特征尺寸与波长可比拟时，电磁场是振荡且传播的，此时常采用波物理来理解和描述该问题.因此计算电磁学的数值方法从求解的问题可分为低频、中频和高频方法，如求解低频问题的低频多层快速多极子方法、求解中频问题的多层快速多极子方法以及求解高频问题的高频近似方法等.

计算电磁学中的数值方法也可分为频域方法（frequency domain）和时域方法（time domain）两大类.频域方法是基于时谐微分和积分方程，如有限元方法（finite element method，FEM）［8－10］、矩量法（method of moments，MoM）［11－12］等，这类方法一次只能求得一个频率点上的响应，多用于窄带问题.当面对瞬态电磁问题时，需要通过对多个频率采样值的傅里叶逆变换得到.时域方法按照时间步进得到相关场量，如时域有限差分法（finite difference time domain，FDTD）［13－15］、时域有限元方法［16－17］、时域多分辨分析法［18］、时域积分方程法［19］、时域间断伽辽金方法［20－21］、时域谱元法［22－23］等，这类方法通常适用于求解在外界激励下场的瞬态变化过程.在求解复杂结构超宽带响应时，时域方法可以一次性获得时域超宽带响应数据.

由于方程形式上可分成积分方程和微分方程，计算电磁学中的数值方法也可划分为基于微分方程的和基于积分方程的方法.基于微分方程的方法包括时域有限差分法、时域有限体积法［24－25］、有限元方法等.基于积分方程的方法包括各类基于边界积分方程与体积分方程的方法，包括矩量法、多层快速多极子方法［26］等.

各种数值计算方法都有优缺点，一个复杂的问题往往难以只依靠一种方法得到很好地解决，需要将多种方法结合起来，互相取长补短，因此各种方法的协同和集成技术日益受到人们的重视，并成为研究的热点之一.

1 国内外研究最新进展

为了更清晰地概述计算电磁学的最新进展，我们从学术研究、商业软件及专用软件三个层次进行论述.高校和研究所主要从事学术研究层次的工作，以更高的计算效率和计算精度的新算法为研究目标，常以程序和论文作为研究成果的体现形式.商业软件主要是由软件公司主导，一些高校或研究所参与部分模块的研发，商业软件面向市场，需要具有良好的通用性和易用性，因此一般会采用最成熟的算法.专用软件介于学术研究和商业软件之间，强调的是计算能力和专用性，这类软件通常与重大项目紧密结合，因此，一般是由政府研究机构主导，并有相关高校和公司参与.

1.1 学术层次

从学术层次来讲，近年国内外研究的最新进展主要表现为五个方面：快速算法、预条件技术、混合方法、基于分而治之（divide and conquer）思想的数值计算技术以及并行计算技术.

1.1.1 快速算法

由于矩量法产生的是一个满阵，用N代表未知量个数，则存储量为O（N2），采用直接求解的计算复杂度为O（N3），而迭代法求解的计算复杂度为O（N2），当未知量N增大时，存储量和计算量都会快速增加，极大地限制了矩量法的求解能力，使其不能满足电大尺寸电磁场问题的计算.快速算法主要是为了解决矩量法求解过程中存储量和计算量过大的问题而发展起来的一类算法，以满足工程中日益增长的对电大尺寸复杂多尺度问题精确模拟的需要.这些方法主要包括快速多极子方法（FMM），多层快速多极子方法（MLFMM）［26］，快速非均匀平面波算法（FIPWA）［27］，自适应积分方法（AIM）［28］，共轭梯度快速傅里叶变换（CG-FFT）［29］等.其中，多层快速多极子算法是一种常用的基于矩量法的快速算法，可以成功地将存储量和计算复杂度降到O（N）或O（N log N）.

快速多极算法（fastmultipolemethod，FMM）是由Greengard和Rokhlyn在20世纪80年代提出，用于拉普拉斯（Laplace）方程的求解，90年代初开始应用于电磁场散射问题的计算.快速多极子方法首先是将离散的未知量划分成若干组，相对于任何一个组，其它组可分为该组的邻近组和远距组两类.邻近组内的未知量的相互作用仍通过矩量法进行计算，而远距组内未知量的相互作用则用快速多极子方法计算，其基本思路是将整个相互作用过程分解为聚集、转移和发散三步，完成远相互作用的高效计算.另外，还有基于矩量法的快速算法研究的小波正交基的应用.利用小波函数具有的局域性和多分辨分析等特性可对矩量法矩阵进行稀疏化处理，从而降低矩量法的计算复杂度.

1.1.2 预条件技术

应用计算电磁学的数值方法求解电磁问题时，得到离散矩阵的条件数往往很差，因此，若直接使用迭代法求解，其迭代速度常常很慢甚至不收敛.选用合适的预条件子可以大大改善离散矩阵的条件数，从而提高迭代法的稳定性和收敛速度.预条件技术的基本思想是将原线性方程组转化为与之同解的但性质更好的线性方程组，然后对这个改善后的方程组进行迭代求解.一个好的预条件子首先应易于构造和应用，其次预处理后的线性方程组还应易于求解.计算电磁学数值方法中常用的预条件技术包括对角预条件、对称超松弛预条件、不完全LU分解预条件、稀疏近似逆预条件等.

卡尔德龙（Calderon）预条件子算得上是近年来计算电磁学界比较成功的预条件技术.在低频问题中电场积分方程对应的积分算子是无界且病态的.然而，根据卡尔德龙（Calderon）等式，电场积分算子的平方等于一个单位算子和一个紧算子之和，因此研究人员提出利用电场积分算子作为自身的预条件子来改善其条件数，即卡尔德龙预条件子［30］.卡尔德龙等式早已为大家所熟知，然而直接利用Rao-Wilton-Glissons（RWG）基函数离散电场积分算子的平方会导致奇异的Gram矩阵，所以一直未能很好地用来构造预条件子.最近，Buffa-Christiansen（BC）基函数［31］的提出和使用可以很好地避免奇异矩阵的生成，使卡尔德龙预条件子真正成为研究热点，并成功地用于改进许多电磁场问题离散矩阵的条件数.

1.1.3 混合方法

为了更好地求解实际工程中遇到的复杂电磁问题，比如涂敷复杂目标的电磁特性分析、电路板及微带天线的辐射散射，以及复杂系统的电磁兼容分析等等，目前很多学者常将各种方法搭配起来使用，形成各种混合方法.常见的混合方法包括基于边界积分方程或体积分方程的方法与基于微分方程的方法的混合、高频近似方法与数值方法的混合、解析方法与数值方法的混合等.比如，针对含有局部复杂精细结构的超电大尺寸目标提出的高频近似方法与数值方法的混合技术，包括弹跳射线法／矩量法混合（SBR／MoM）、物理光学／矩量法混合（PO／MoM）、几何绕射理论／矩量法混合（GTD／MoM）等等［31－33］.由于完全使用数值方法来处理超电大尺寸目标往往超出了目前计算机的计算能力，而单纯使用高频近似方法又不能得到足够精确的近场，所以这种相互结合，发挥各自的优势的方案就应运而生.当然，引入了高频近似方法在赢得了速度和空间的同时，在一定程度上也损失了精度.

而基于边界积分方程的方法与基于微分方程的方法的混合技术，多用于含有复杂细节目标体和复杂介质的问题.这类方法中比较典型的是有限元边界元混合法（FEBI）［34］.该类方法中边界积分方程的选择灵活多样，如电场积分方程（EFIE）、磁场积分方程（MFIE）、组合场积分方程（CFIE）等等，需要注意的是不同边界积分方程的选择会直接影响FEBI矩阵的条件数，导致不同的计算精度和效率，一些还会导致内谐振问题.边界积分方程部分可以利用矩量法及其快速算法进行计算，边界所围的内部区域通常采用有限元方法.边界积分方程的使用能够精确地描述电磁场在无限远处的辐射条件，为有限元方法提供了精确边界条件，不仅提高了计算精度，而且大大减小了有限元方法的求解区域.

1.1.4 基于分而治之（divide and conquer）思想的数值计算技术

面对所要求解的电大尺寸多尺度复杂电磁场问题，尽管目前计算机在运算速度和存储能力上都发展迅速，仍无法满足O（N2）和O（N3）的计算复杂度和存储需求.对于一个超大规模问题，近年来，一些学者利用分而治之的思想发展出了高效的数值方法，如等效原理算法（equivalence principle algorithm，EPA）［35］、多求解器区域分解方法（multi-solver domain decomposition method） 等，可以将整个计算成本降低到一个合理的水平.区域分解方法是最直观的分而治之方法，它也可以看作是一类预条件子.分而治之简单来讲，首先把一个大问题划分成一些较小的子问题，然后将所有子问题的一定精度的数值解进行整合，从而，得到原问题较低阶的数值解.由于计算量分配到了各个子问题，因此很自然地可以使用分布式的计算机系统配合分而治之的方法来求解电大尺寸多尺度复杂电磁场问题.

在EPA算法中，首先引入一些人工等效表面将需要计算的目标体分成多个子目标体，并利用等效表面上的切向磁场和电场定义等效电流和磁流作为未知量.根据惠更斯原理，可通过每个等效表面内部各自的相互作用和等效表面之间作用的相互转移因子来实现子目标体之间的相互作用.

另一个基于分而治之思想的方法是多求解器区域分解方法.与等效原理算法不同，该方法不需要引入人工等效表面，而是根据计算区域各部分的特点，将求解区域直接划分成一些子区域，在每个子区域中还需要选择合适的离散网格和数值方法进行求解.同时，需要在子区域间的交界面上建立合适的传输条件来满足交界面上的连续性条件.然后，应用整合技术来实现各区域之间信息的交换.

此外，时域间断伽辽金方法（discontinuous Galerkin time-domain method，DGTD）是近年来发展起来的一种时域区域分解方法.它支持并行计算技术和非协调网格技术，可以处理各种不同形状的单元，并获得高阶精度.

1.1.5 并行计算技术

目前，如果只使用单CPU计算机的串行计算，很难满足复杂电磁场问题的大规模计算的需求.因此，开发采用多CPU的并行计算机系统成为高性能计算机的发展趋势，为此必须相应地发展电磁场问题的并行计算技术.并行计算，也称为高性能计算，是在现有的算法基础上，增加计算资源等硬件设施，把待求解的问题分解为许多小问题，分别在不同的处理器上求解，通过网络等方式实现进程间的通信，最后得到需要的解，从而实现联合求解大问题.

在计算电磁学的数值方法并行计算技术的研究中，最早发展的是时域有限差分法的并行算法.在时域有限差分方法的Yee网格上，每一网格点上的电场或磁场只与其周围相邻点的磁场或电场及其上一时间步的场值有关.其固有的局部化特征使得每个子区域可单独由一台处理器进行计算，且在迭代过程中不同子区域之间的通信量很小，因而易于获得较高的并行效率.目前，时域有限差分方法的并行算法已应用于很多复杂三维电磁场问题的计算［1］.

虽然多层快速多极子算法的计算复杂度可达到O（N）或O（N log N），但是当未知量个数N很大时，单个CPU往往很难满足计算需求.自1999年美国伊利诺伊大学成功开发了可扩展并行化程序ScaleME（scaleable multipole engine），并在并行多层快速多极子算法的研究工作并取得了一系列成果.为了求解更大规模问题，近年来许多学者在改进多层快速多极子算法的并行化方面做出了许多努力，特别是在发展新的分区技术和分布格式方面，如混合分区技术、分层并行策略等［37－39］.

1.2 商业软件

计算电磁商业软件的特点是以成熟的数值方法为基础开发，以PC平台为主的通用软件.在当前的电磁相关科研甚至产业界，商用计算电磁软件以其良好的建模能力和用户界面、丰富的分析功能、大量的应用算例，已经占据了统治地位.由于依靠商业手段和市场规律不断发展的，商业软件在成熟性和实用性方面具有天然优势.基于有限元类方法的软件包括HFSS，POISSON／SUPERFISH，QUICKFIELD，FIELD PRECISION等；基于时域有限差分类方法的软件包括：CST MWS，FLOEMC，XFDTD，OPTIFDTD，EMPIRE，SEMCAD，FIDELITY等，基于矩量法的软件包括：FEKO，IE3D，SONNET，MOMENTUM等（其中FEKO初步实现了高频近似方法和矩量法的混合计算），具有多物理场计算功能的软件包括ANSYS，COMSOL.商业软件的发展趋势是结合高性能计算和多物理计算，以收购和联合研发方式不断完备其方法库，强化其工程计算能力.

1.3 专用软件

尽管商业软件很大程度上满足了一般电磁模拟的需要，但是由于其计算平台的资源限制，以及对市场及通用性的优先考虑，并不具备处理以平台级或系统级电磁模拟为代表的大型复杂电磁问题的能力.为了弥补这一缺陷，美国和欧盟均不断开发专业的模拟软件，这些软件通常利用最新的算法成果，集成多种算法，建立在大规模计算平台上，并将工程实践经验融合其中，提供专家级的系统模拟解决方案.专业软件通常在政府及军方主持下开发，安排有专门的系统级实验项目用于校验程序.专用软件的使用权无一例外地受到政府的严格控制，正常渠道不可能获得.有限的报道和文章均只限于展示其计算能力，技术细节从不涉及.这些软件包括：GEMACS（general electromagneticmodel for the analysis of complex systems，频域模拟）和TMAX（时域模拟），XPATCH（飞行器散射分析程序），ADF（antenna design framework）天线设计平台、Ship EDF（ship electromagnetic de-sign frame）舰船电磁设计平台软件以及电磁兼容方面的SEMCAP（系统和电磁兼容分析程序），IEMCAP（系统内电磁兼容分析程序）和E3EXPERT（电磁环境效应专家系统），SEMCA（舰船EMC分析）等.限于篇幅，下面只介绍几个主要超大规模并行高性能计算计划支持下的计算电磁学相关专用软件发展状况.

1）美国能源部的SCIDAC（scientific discovery through advanced computing）：

作为高能物理研究的主要工具——加速器系统是典型的电大、多尺度、多物理模拟目标，对计算电磁能力有极高的要求.为了满足二十一世纪射频加速器的研制需要，SCIDAC已经支持了两期先进计算项目，即Scidac1（1996－2001）中的 AST（accelerator science＆technology）和 Scidac2（2007－2011）中的 COMPASS（community petascale project for accelerator science and simulation）.其目标是通过高置信度电磁模拟实现大型加速器系统的设计和优化（design and optimization of large accelerator systems through high-fidelity electromagnetic simulations）.在这个计划中，广泛应用了诸如高阶有限元全电磁模拟、电磁／热／应力多物理模拟、并行自适应网格加密、动态负载平衡、并行可视化及交互等先进技术.

2）美国国防部的HPCMP（高性能计算现代化计划，DOD high performance computingmodernization project）：

定向能武器虚拟样机（virtual prototyping of directed energy weapons）是HPCMP计划支持的项目之一，其主干程序ICEPIC的技术含量明显高于高功率微波界目前常用的商用软件：MAGIC、KARAT和OOPIC，其具有的超大规模计算能力使得对高功率微波源甚至系统进行三维全波模拟成为可能.此外，专用于大型天线和系统级耦合效应模拟的计算电磁程序也都在该计划支持下得到快速发展.

3）欧盟的HIRF-SE（high intensity radiated fields synthetic environment）：

高强度辐射场集成环境（HIRF-SE）项目（2008－2012）是由欧盟委员会第七框架计划资助，包括在电磁兼容计算，电磁建模，飞行器测试，验证以及模拟等方面具有良好基础的43家合作单位，总经费达2650万欧元.该项目旨在为航空工业提供一个在设计开发阶段使用的数值模拟计算框架，用来保证飞行器在全寿命周期中的电磁性能，同时显著减少对飞行器验证的测试.该集成环境是通过将已有的数值模拟技术进行有效集成，使各种方法实现协同计算，建立系统化求解器来处理复杂问题.

2 复杂电磁环境数值模拟技术

2.1 复杂电磁环境

以电磁波辐射、传播、接收为基础的各类使用电磁波的军用、民用活动，以及科学实验与研究行为是电磁环境形成的基础.电磁环境的构成要素包括人为电磁辐射（有意和无意的电磁辐射），自然电磁辐射（静电、雷电等）以及辐射传播因素（电离层、地理环境和气象环境等）.国内和美国在关于复杂电磁环境概念的提法上稍有不同，国内称为复杂电磁环境，是指在一定空间内，由空域、时域、频域和能域上分布密集、数量繁多、样式复杂、动态随机的多种电磁信号交叠而成的，对设备和人员等构成一定影响的电磁环境.而美国则称为电磁环境效应，指以电磁场／波作为信息／能量载体／工作媒介的设备／系统／平台在复杂电磁环境中的响应或状态.复杂电磁环境数值模拟的应用前景十分广泛，如军用方面：由多个密集电子平台构成的海陆空天四维电磁空间的场景模拟，以及重要电子系统在特定环境中的性能分析；民用方面：信息领域重大应用（如无线通讯，铁路，电力，民用航天及航空等）模拟，以及重要科学研究平台及民用电子系统在特定环境中的性能分析.因此，复杂电磁环境是当前军用、民用信息领域关注的焦点问题之一.北京应用物理与计算数学研究所正是在这个背景下开展了复杂电磁环境数值模拟平台的论证及构件工作.

从计算电磁学的角度看，复杂电磁环境数值模拟的复杂性主要体现在激励源的多时间尺度、全频谱特性；边界条件的多空间尺度、多介质特性；器件机理的多种物理特性以及系统本身的多空间尺度特性等.这些特性对复杂电磁环境高效能高置信的数值模拟提出了挑战.根据复杂电磁环境的几何尺度、包含物理问题的特性、所关注的具体物理量等方面的综合考虑，我们将复杂电磁环境不严格地分为区域级、平台级以及器件级电磁环境.

尽管计算电磁学已形成了一些成熟的通用商用软件，可用于不同层次复杂电磁环境的数值模拟，如AREPS（区域）、WinProp（区域）、REMCOM（区域－平台）、ANSYS（平台）、CST（平台－电路）、WiPL-D（平台－电路）、EMC Studio（平台－电路）等.但在相当长的时期内，高性能微机／工作站加商用软件的模式在面对大规模复杂电磁环境问题模拟时常常无能为力，而这些问题正是国防领域和高端商用领域所经常遇到的.大规模复杂电磁环境问题的科学工程计算不仅对计算资源及高性能计算有强烈需求，而且需要借助于计算电磁学目前在超电大、多尺度、多介质、多物理的协同电磁高性能计算方面的先进数值方法.因此，立足于高性能计算领域的已有特色及优势，与建立在成熟计算技术基础上的主流商业软件形成互补，避免重复性劳动，解决大规模复杂电磁环境问题计算能力的“有无”问题就成为第一步目标.

2.2 复杂电磁环境数值模拟软件平台体系

近年来，以面向大规模复杂电磁环境问题工程计算为发展目标，以传统计算电磁学与高性能科学计算无缝融合为特点，在北京应用物理与计算数学研究所的计算平台及JASMIN（J parallel adaptive structured mesh applications infrastructure，并行自适应结构网格应用支撑软件框架）和 JAUMIN（J parallel adaptive unstructured mesh applications infrastructure，并行自适应非结构网格应用支撑软件框架）上提出并正在建立复杂电磁环境数值模拟软件平台.JASMIN和JAUMIN是针对科学计算中的结构和非结构网格应用，通过封装高性能数据结构，集成成熟数值算法、屏蔽大规模并行和网格自适应计算技术，支撑物理建模、数值方法、高性能算法的创新研究，加速研制可有效使用现代高性能计算机的并行自适应计算应用程序，从而显著降低程序开发成本.在JASMIN和JAUMIN基础上，用户无需了解并行计算、自适应网格剖分、高性能数值算法等细节，而只需专注于物理模型和计算方法.

从所要求解的纷繁复杂的电磁工程问题的超电大、多尺度、多介质、多物理等特性出发，基于高效能计算环境，采用多种方法有机集成的方式形成软件平台，以保持计算方法的持续可扩展性，并通过基于机理／数据的混合可计算建模及接口设计，保持物理个性的可分离性及可扩展性.在充分了解国内外发展现状的基础上，将国际／国内计算电磁学的最新成果融入到软件平台的设计和研制中，以算法模块联合研究的形式发挥国内优势高校的研究力量.

依据复杂电磁环境数值模拟的上述三个层次，以及不同物理层次所需模拟软件算法共性基础构架的不同，复杂电磁环境数值模拟软件平台的软件体系由区域级电磁环境模拟软件、平台级全波电磁模拟软件以及器件级多物理电磁模拟软件三套软件包共同构成，整体体系规划如图1所示.该软件体系的总体目标是重点突破区域级／场景电磁模拟、电大多尺度结构全波模拟、多物理电磁计算、大规模并行计算等关键技术，围绕明确需求牵引，在高性能计算环境中构建能力型复杂电磁环境数值模拟平台，为高价值目标提供基于高性能计算的复杂电磁系统分析、优化及评估解决方案，为国内重大电磁工程问题快速定制高端专用计算平台.

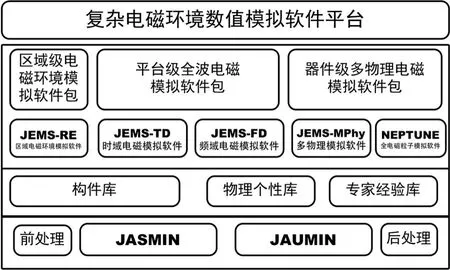
图1 复杂电磁环境数值模拟软件平台体系规划Fig.1 A general layout of numerical simulation platform of E3

区域级电磁模拟软件是依托高性能计算机系统，针对平方公里以上区域的典型军用／民用场景，在综合考虑多变地形地貌（如丘陵、森林、植被、海洋）及气象（考虑风、霜、雨、雪、雾）等因素的条件下，具备对由不同参数和位置的多个电磁辐射源所形成的动态电磁环境进行高效数值模拟的能力.获取该区域的矢量电磁场时域、空域、频域分布.区域级电磁模拟软件采用的关键技术是三维矢量以及时域抛物方程方法，且发展了抛物方程方法与射线方法、有限差分方法的混合计算技术.另外，还采用了多重网格大规模并行技术、电磁环境一体化可计算建模技术、不同地貌的大地回波特性模拟方法以及基于激光成像／地理信息系统的海量数据前处理及后处理技术.

平台级全波电磁模拟软件主要是针对典型的平台级目标（超电大多尺度目标，如大功率微波／毫米波／太赫兹发射系统、飞行器等），通过精确建模及全波电磁模拟，获取包括近场和远场在内的所有电磁特征（如平台级目标特性RCS、平台级电磁兼容等），具备构建电大复杂目标的电磁虚拟样机的能力.平台级全波电磁模拟软件从时域和频域两个方面发展电大多尺度多介质电磁模拟技术，以具备高性能计算能力.时域部分主要采用基于HPA-adaptive模式的时域多算法求解技术，而频域部分采用基于非重叠非匹配网格区域分解方法的多算法求解技术.配合以并行网格剖分及并行计算技术、基于耦合波方法的电大馈线系统的快速计算技术以及电磁场／电路协同计算技术.

器件级多物理电磁模拟软件则是针对电子系统在特定环境中的特性分析，基于麦克斯韦方程构建多物理求解框架，突破多物理计算及瞬态电路／电磁场协同计算和多物理大规模并行等关键技术，具备能普遍用于器件级多物理电磁模拟及粒子模拟的大规模并行计算能力.多物理电磁计算指除了求解麦克斯韦方程外，由于多个物理场的多向强耦合关系，还必须联立求解多个方程组.器件级多物理电磁模拟软件的关键技术是时域多物理求解框架及时间尺度统一算法，并实现多层紧耦合协同算法和器件物理可计算建模技术.

2.3 典型算例

目前已自主及联合研制了多个相关程序，并在北京应用物理与计算数学研究所的计算平台及JASMIN上调试成功.已实现的算法模块包括：三维全电磁粒子模拟模块（NEPTUNE3D，自主），频域积分方程求解器——多层快速多极子算法（JEMS-MLFMM，联合电子科技大学），时域微分方程求解器——时域有限差分算法（JEMS-FDTD，联合西南交通大学）和多物理场（电磁、载流子、热）时域混合求解器（联合四川大学）.下面是一些典型算例.

1）高功率微波器件设计与分析

通过三维全电磁粒子模拟，对高功率微波源——磁绝缘线振荡器进行了物理分析与优化设计.数值模拟揭示了器件内部电子束与电磁波互相用并形成群聚的物理过程及图像，模拟结果（见图2）与实验结果吻合.总网格数1 380万，总粒子数300万，物理过程20纳秒，运行20 000时间步，在1 024 CPU核上并行计算1.3小时.

图2 磁绝缘线振荡器（MILO）的三维粒子模拟Fig.2 3D PIC simulation of MILO

2）真实建筑物的辐照电磁效应分析

计算整栋真实建筑物在外界斜入射平面波照射下建筑物内的电磁分布，用以分析其电磁屏蔽效应.建筑物为三层结构，电尺寸超过200波长.结构与真实情况相同，具有包括多种墙体、地板、玻璃、金属框架、木门、铁门等在内的复杂结构，其材料电属性通过实测获得.对该类电大尺寸问题的全波数值模拟是国内首次实现.网格总数125亿，使用5 760处理器核并行计算，结果如图3.

图3 建筑物的结构示意图和建筑物内频域电场分布（1.5 GHz）Fig.3 A schematic of building and electric field in the building（1.5 GHz）

3）真实计算机机箱电磁屏蔽效能分析

对计算机机箱在外界脉冲电磁波照射下的电磁响应进行数值模拟，用以分析计算机机箱的电磁屏蔽效能.计算模型参照真实计算机机箱严格建模，尺寸为250 mm×500 mm×600 mm，箱体表面分布有各种形状散热孔，背部有三芯电源线，另外还包括多种线缆、主板、设备托架等真实结构.数值模拟显示了电磁波通过孔缝、线缆耦合进入机箱的物理过程以及各频点处的电磁稳态分布，计算结果（如图4）与实测结果吻合.网格总数6亿，使用天河－1 A超级计算机上80 000处理器核并行计算.

图4 计算机机箱的瞬态电场分布（a）和2.8 GHz频域电场分布（b）Fig.4 Transient electric field in a computer case（a）and electric field at2.8 GHz（b）

4）飞行器整机瞬态电磁特性

对L波段平面波沿飞机头部正入射照射下的飞行器进行数值模拟，结果如图5，用以分析飞行器整机瞬态电磁特性.计算模型参照瑞典Saab公司的JAS-39（Gripen）型真实飞行器严格建模，尺寸为17 m×10 m×5.3 m通过数值模拟给出了飞行器的2 GHz频点的电场近场分布以及瞬态电场近场分布.网格总数达72亿.

3 高性能计算电磁学的发展趋势

计算电磁学横跨计算数学、电磁理论、计算机技术等多个学科，相关学科的快速发展，不仅推动计算电磁学的各种数值方法不断改进，同时也向计算电磁学的发展提出了更多要求.综合考虑以复杂电磁环境问题为代表的国防高技术领域的应用需求以及计算电磁学技术的发展现状，我们提出了对电磁模拟技术未来发展的要求，即：面向并紧密结合国防重大应用，为大规模复杂电磁环境相关问题提供高性能高置信计算仿真平台.这些重大应用可能包括：建立复杂场景下的电波传播模型；系统级目标的散射、耦合效应及电磁效能评估；毫米波、亚毫米波／THz电磁系统的整体数值模拟，高能物理实验系统的电磁模拟（RF加速器、等离子体）等.

图5 瞬态电场近场分布Fig.5 Transient electric field near surface

具体地讲，就是在现有基础上继续完善在高性能计算平台下的复杂电磁环境专用软件系统，逐渐使其具备大规模、多尺度、多介质、多算法、多物理模拟的计算能力，重点的发展方向包括大规模高性能计算技术、多物理计算技术和协同计算技术，即

1）发展高性能计算支撑环境下的计算电磁学方法集成.在完善已有算法代码的基础上逐渐增加新的算法模块和物理功能模块.例如平台级时域模块中采用基于HPA-adaptive的时域多算法技术，除了已开发的JEMS-FDTD外，还将发展非均匀网格FDTD、高阶FDTD、时域有限元方法等，并实现并行自适应网格加密（AMR）技术；在平台级频域模块中以基于非重叠非匹配网格区域分解方法的多算法求解技术为发展思路，在实现并完善JEMS-MLFMM的基础上，继续发展有限元方法、高频近似方法等主要频域方法，并设计有效的区域分解框架，实现各种频域方法的高效协同计算.升级并行支撑框架以支持灵活度更高、边界拟合能力更强的非结构化网格算法（如有限元方法）等等.

2）在大规模并行计算平台上，以全局随机优化算法、数据挖掘和人工智能技术为基础逐渐形成器件级的自动化工程设计能力.应当注意，并非只有超大和超复杂的问题才需要大规模并行计算.对中小问题而言，大规模并行计算是实现全局优化的必要条件.比如，在当前普遍采用二维全电磁模拟软件进行的高功率微波源模拟和设计中，单机单次计算时间并不长，但是如果要求对多个参数进行全局自动优化，就通常需要进行成千上万次的运算才能替代一般的人工调试，这样的计算量对单机而言几乎是不可实现的.我们已经初步实现了基于遗传算法和全电磁例子模拟的优化程序，在对MILO等典型高功率微波源的测试中已经取得了不错的效果.

3）在高性能计算平台上建立复杂工程目标的通用建模及并行网格剖分能力（前处理），完善并行可视化交互能力（后处理）.图形化建模、自动网格剖分以及良好的结果可视化历来是商业软件的长项，是保障其实用性和通用性的基础，因而也占据了其软件成本的较大比例.但对于复杂电磁环境中的超电大、多尺度、多介质复杂目标而言，前后处理中的海量数据将成为计算中的主要瓶颈，其对内存和计算时间的要求远非一般商业软件和通用计算平台所能承受.

4）逐渐建立和完善协同计算能力.这里所指的协同计算是一个大概念，或者称是一套思想，它应包括多物理协同（如电磁、热、力）；系统的物理分级协同（如场／路／信号协同，电磁拓扑）；多算法协同（如混合算法、区域分解）以及计算与实验数据／库的协同／融合等各个方面.必须强调，尽管近年来的专用软件研制工作以实现大规模并行计算作为首要目标，但客观地讲，仅仅追求大规模计算对于工程计算而言是远远不够的.一方面，由于计算机能力提高的摩尔定律远不能与计算复杂度的提高速度相比，因此计算代价与计算需求及精度之间的矛盾将永远存在；另一方面，对于很多现实面临的复杂电磁问题（比如系统级电磁兼容或电磁环境效应分析和评估等），即使拥有超级计算机和最好的计算电磁学代码可用，也可以断言确定的数值解没有什么价值.对于合格的物理设计和实验人员而言，最好的模拟工具是基于协同概念构成的专家系统或半实物仿真系统，而绝对不是单纯依赖海量计算、可视化及优化就完成设计和实验过程的傻瓜软件.

［1］王长清.现代计算电磁学基础［M］.第一版.北京：北京大学出版社，2005.

［2］James G L.Geometrical theory of diffraction for electromagnetic waves［M］.Chicago，IL：Peregrinus，1976.

［3］Michaeli A.Equivalent edge currents for arbitrary aspects of observation［J］.IEEE Trans Antennas Propag，1995，43（2）：162－169.

［4］Millar R F.An approximate theory of the diffraction of an electromagnetic wave by an aperture in a plane screen［J］.Proc IEEE，1993，81（12）：1658－1684.

［5］Stratton JA.Electromagnetic theory［M］.New York：McGraw-Hill，1941.

［6］盛新庆.计算电磁学要论［M］.第1版.北京：科学出版社，2004.

［7］Chew WJ，Jiang L J.Overview of large-scale computing：The past，the present，and the future［J］.Proceedings of The IEEE，2013，101（2）：227－241.

［8］Silvester P P，Ferrari R L.Finite elements for electrical engineering［M］.Cambridge：Cambridge University Press，1983.

［9］Zienkiewicz O C，Taylor R L.The finite elementmethod［M］.4th ed.New York：McGraw-Hill，1989.

［10］Jin JM.The finite elementmethod in electromagnetics［M］.New York：Wiley，1993.

［11］Harrington R F.Field computation bymomentmethods［M］.2nd ed.New York：IEEE Press，1993.

［12］Peterson A F，Ray S L，Mittra R.Computationalmethods for electromagnetics［M］.New York：IEEE Press，1998.

［13］Taflove A.Computational electrodynamics：The finite difference time domain approach［M］.Artech House，Norwood，MA：1995.

［14］Gustafsson B，Kreiss H O，Oliger J.Time dependent problems and differencemethods［M］.New York：Wiley，1995.

［15］葛德彪，闫玉波.电磁波时域有限差分方法［M］.西安：西安电子科技大学出版社，2002.

［16］Cangellaris A，Lin C，Mei K.Point-matched time domain finite elementmethods for electromagnetic radiation and scattering［J］.IEEE Trans Antennas Propag，1987，35（10）：1160－1173.

［17］Lee JF，Sacks Z.Whitney elements time domain（WETD）methods［J］.IEEE Trans Magn，1995，31（3）：1325－1329.

［18］Krumpholz M，Katehi L P B.MRTD：New time-domain schemes based on multiresolution analysis［J］.IEEE Trans Microwave Theory，1996，44（4）：555－561.

［19］Manara G，Monorchio A，ReggianniniR.A space-time discretization criterion for a stable time-marching solution of the electric field integral equation［J］.IEEE Trans Antennas Propagat，1997，45：527－532.

［20］Cockburn B，Li F，Shu C W.Locally divergence-free discontinuous Galerkin methods for the Maxwell equations［J］.J Comput Phys，2004，194（2）：588－610.

［21］Lu T，Zhang P，Cai W.Discontinuous Galerkin methods for dispersive and lossy Maxwell's equations and PML boundary conditions［J］.JComput Phys，2004，200（2）：549－580.

［22］Lee JH，Chen J，Liu Q H.A 3-D discontinuous spectral element time-domain method for Maxwell's equations［J］.IEEE Trans Antennas Propag，2009，57（9）：2666－2674.

［23］Lee JH，Liu Q H.An efficient 3-D spectral elementmethod for Schrodinger equation in nanodevice simulation［J］.IEEE Trans Comput Aided Design Integr Circuits Syst，2005，24（12）：1848－1858.

［24］Shankar V，Mohammadian A H，Hall WF.A time-domain finite-volume treatment for the Maxwell equations［J］. Electromagnetics，1990，10（1）：127－145.

［25］Mohammadian A H，Shankar V，HallWF.Computation of electromagnetic scattering and radiation using a time-domain finitevolume discretization procedure［J］.Comput Phys Commun，1991，68（1－3）：175－196.

［26］Chew WC，Jin J，Michielssen E，Song JM.Fastand efficientalgorithms in computational electromagnetics［M］.MA：Artech House，2001.

［27］Hu B，Chew WC，Michielssen E，Zhao J.An improved fast steepest descentalgorithm for the fastanalysis of two-dimensional scattering problems［J］.Radio Science，1999，34（4）：759－772.

［28］Bleszynski E，Bleszynski M，Jaroszewicz T.AIM：Adaptive integralmethod for solving large-scale electromagnetic scattering and radiation problems［J］.Radio Science，1996，31（5）：1225－1251.

［29］Zwamborn P，van den Berg P M.The three-dimensional weak form of conjugate gradient FFT method for solving scatteringproblems［J］.IEEE Trans Microw Theory Tech，1992，40：1757－1766.

［30］Andriulli F P，Cools K，Bagci H，Olyslager F，Buffa A，Christiansen S，Michielssen E.A multiplicative Calderon preconditioner for the electric field integral equation［J］.IEEE Trans Antennas Propag，2008，56（8）：2398－2412.

［31］Buffa A，Christiansen S.A dual finite element complex on the barycentric refinement［J］.Mathematics of Computation，2007，76（260）：1743－1769.

［31］Jin JM，Ling F，Carolan S T，Song JM，Gibson WC，Chew WC，Lu C C，Kipp R.A hybrid SBR／MoMtechnique for analysis of scattering from small protrusions on a large conducting body［J］.IEEE Transactions on Antennas and Propagation，1998，46（9）：1349－1357.

［32］Jakobus U，Landstorfer FM.Improved PO-MMhybrid formulation for scattering from three-dimensional perfectly conducting bodies of arbitrary shape［J］.IEEE Trans Antennas Propag，1995，43（2）：162－169.

［33］Thiele G A，Newhouse TH.A hybrid technique for combiningmomentmethodswith the geometrical theory of diffraction［J］. IEEE Transactions on Antennas and Propagation，1975，23：62－69.

［34］Sheng X Q，Jin JM，Song JM，Lu CC，Chew WC.On the formulation of hybrid finite elementboundary integralmethods for 3D scattering［J］.IEEE Trans Antennas Propagat，1998，46（3）：303－311.

［35］LiMK，Chew WC，Jiang L J.A domain decomposition scheme based on equivalence theorem［J］.Microw Opt Technol Lett，2006，48（9）：1853－1857.

［36］Lee SC，VouvakisMN，Lee JF.A non-overlapping domain decompositionmethod with non-matching grids formodeling large finite antenna arrays［J］.JComput Phys，2005，203（1）：1－21.

［37］Velamparambil S，Chew WC，Song J.10million unknowns：Is it thatbig？［J］.IEEE Antennas Propag Mag，2003，45（2）：43－58.

［38］Ergul O，Gurel L.Hierarchical parallelization strategy formultilevel fastmultipole algorithm in computational electromagnetics［J］.Electron Lett，2008，44（1）：3－5.

［39］Gurel L，Ergul O.Hierarchical parallelization of the multilevel fastmultipole algorithm（MLFMA）［J］.Proceedings of the IEEE.2013，101（2）：332－341.

Com putational Electromagnetics and Applications in Numerical Simulation of Electromagnetic Environmental Effects and Development Tendency

ZHOU Haijing1，2，LIU Yang1，2，LIHanyu1，2，DONG Ye1，2，LIAO Cheng3，DONG Zhiwei1，2，MO Zeyao1，2
（1.Institute of Applied Physics and Computational Mathematics，Beijing 100094，China；2.Software Center for High Performance Numerical Simulation，CAEP，Beijing 100088，China；3.Electromagnetics Institute，Southwest Jiaotong University，Chengdu 610031，China）

A brief introduction to development history of computational electromagnetics（CEM）and numericalmethods in CEMis provided.In addition，we discuss up-to-date progress of CEMin scientific researches，commercial softwares and proprietary softwares. Considering applications of electromagnetics environmental effects（E3），we present development of our numerical simulation platform of E3.Finally，future trends of development in E3 are shown.

computational electromagnetics；electromagnetic environmental effects；high performance computing

date： 2013－12－02；Revised date： 2014－03－05

O562

R

1001-246X（2014）04-0379-11

2013－12－02；

2014－03－05

国家重点基础研究发展计划（2013CB328904），国家自然科学基金（61201113和11305015），中物院复杂电磁环境科学与技术重点实验室课题及国家自然科学基金委－中物院NSAF联合基金（U1330109）资助项目

周海京 （1970－），男，博士，研究员，中物院高性能数值模拟软件中心首席专家，主要从事高功率电磁学及计算电磁学的应用研究

刘阳，E-mail：liu_yang＠iapcm.ac.cn