基于Foliation条件的离散动力系统二维流形计算

贾 蒙

（新乡学院机电工程学院，河南新乡 453003）

基于Foliation条件的离散动力系统二维流形计算

贾 蒙

（新乡学院机电工程学院，河南新乡 453003）

研究离散动力系统双曲不动点的二维流形计算，利用不变流形轨道上Jacobian矩阵能够传递导数这一特殊性质，提出一种新的一维流形计算方法，通过预测－校正两个步骤迅速确定流形上新网格点，避免重复计算，并简化精度控制条件.在此基础上，将基于流形面Foliation条件进行推广，推广后的Foliation条件能够控制二维流形上的一维子流形的增长速度，从而实现二维流形在各个方向上的均匀增长.此外，算法可以同时用于二维稳定和不稳定流形的计算.以超混沌三维Hénon映射和具有蝶形吸引子的Lorenz系统为例验证了算法的有效性.

离散动力系统；稳定流形；不稳定流形；导数传递；三维Hénon映射；Lorenz系统；混沌吸引子

0 引言

稳定流形和不稳定流形在分析系统的动力学特性中起着非常重要的作用，它们充当着不同吸引子吸引域的边界，将全空间划分为多个具有不同动力特性的不变子空间；而当稳定与不稳定流形相交时，就会引起同宿、异宿以及混沌等复杂动力学行为的出现.

流形计算作为动力系统分析的一种几何方法，一直以来都受到研究人员的重视.研究的对象主要有两类系统：连续动力系统（向量场）和离散动力系统.连续动力系统一般以微分方程的形式来表示，其一维流形只需通过积分求解初值问题就能得到，比较简单，二维流形计算就变得困难多了：其中一个最主要的问题是当系统的两个稳定（或不稳定）特征值的比值较大时，流形轨道在各个方向上的增长速度不均，而且轨道朝其中一个特征值方向汇集，从而使得计算的结果变差.针对这个问题，国内外的学者给出了许多不同解决办法，详见文献［1－7］.

离散动力系统一般以映射的形式出现，所以有时也称作映射动力系统.离散动力系统的流形计算比较困难，与连续动力系统的流形计算相比，它的一个重要特点是轨道上新网格点对轨道上已有的网格点的依赖性，也就是说，新网格点必须是通过已有网格点或其插值经过映射后才能得到；而连续动力系统的流形计算是通过求解初值问题来计算的，所以只有给定一个出发点，就能计算之后的轨道，而无需考虑出发点之前轨道的状态.这种依赖性的存在，使得离散动力系统的流形计算更为困难.

You［8］，Simó［9］，Parker和Chua［10］，Hobson［11］给出了基域迭代的改进算法.Bernd Krauskopf和Hinke Osinga［12－13］通过每步向流形中加入一个离散点来增长流形，结合曲率控制技术，使得流形的增长速度由流形的局部曲率来决定，该算法能够有效展示流形的细节.与此思想类似，文献［14］中提出的算法能够在逆映射不能显式表达的情况下计算系统的一维稳定流形，而之前提到的大部分算法都是把系统的稳定流形当作其逆映射的不稳定流形来计算的.Dellnitz和Hohmann提出的细分法［15］也能有效地计算一维流形；Danny Fundinger［16］的算法与此思想类似.以上算法在计算的快速性上都有待提高.一维流形计算的问题没有有效地解决，所以二维流形的计算就显得更为困难了，除了要面对计算向量场二维流形时的困难，还要牵扯到插值点原像的搜索问题，并且插值点之后的轨道计算对于插值点之前的轨道存在依赖性，所以就不得不对插值点之前原本不存在的轨道也进行插值，从而使计算变得尤为复杂.目前对于离散系统二维流形的算法很少，文献［17］中提出了一种应用Foliation条件的算法，该算法比较好地解决了流形各向增长速度不均的问题，实际上与向量场二维流形算法 是同一算法，该算法默认新网格点的原像都处于当前流形边界上，很多时候这与实际情况是不符的，所以应用受到限制.国内在相关方面的研究较少，文献［7］提出对于一维流形的计算，最基本的方法是对基域内的有限个离散点进行迭代，这种算法操作简单，计算速度快，但在迭代过程中点的分离可能导致在基域上相距很近的两个点经迭代后得到的像间距变得很大，从而错过流形的细节，使得计算的精度变差.文献［18］提出一种预估流形增长速度的一维流形算法，在此基础上，提出了一种快速的二维流形计算方法，但是该算法也没有解决流形各向增长速度不均的问题进行处理.文献［21］提出的方法仍然不能反映一维子流形的细节特性.文献［22］提出了典型Foppl-von Karman（F-K）理论结合全局分形理论进行非线性系统的流形计算，针对某些特定系统取得一定成果，但是该方法仍不能普及到所有的非线性系统流形计算中.

一维流形计算是二维流形计算的基础，本文在提出一种快速的一维流形算法的基础上，对Foliation条件进行推广，提出一种新的二维流形计算方法，该算法很好地保证了二维流形在各个方向上的均匀增长，并巧妙地避免了新网格点的原像搜索问题.

1 流形的基本概念

设F：Rn→Rn为一个保向的微分同胚映射函数

对于系统（1），若存在x0，满足F（x0） ＝x0，则称x0为系统的不动点．A为x0处的雅各比矩阵A ＝DF（x0）＝［∂fi／∂xj］（x0）．若矩阵A的特征值的模都不等于1，那么x0就是一个双曲不动点；其中模小于1的特征值叫做稳定特征值，其对应的特征向量｛v1，v2，…，vl｝张成稳定特征空间Es；模大于1的特征值叫做不稳定特征值，它们对应的特征向量｛vl＋1，vl＋2，…，vn｝张成不稳定特征空间Eu．全空间Rn＝Es⊕Eu．

定理1设x0是保向微分同胚映射函数F的一个双曲不动点，则在x0的邻域U内存在局部稳定和不稳定流形

从上面的定义可知，全局流形就是局部流形在映射F迭代下得到的像．其中全局稳定流形是局部稳定流形在映射F下进行反向迭代得到的像，而全局不稳定流形是局部不稳定流形在映射F下进行正向迭代得到的像，迭代的方向与其直接定义有所区别.

2 一维流形的计算

一维流形简单看来就是一条满足特殊条件的曲线，其特殊性之一就在于：对于处于流形轨道上的任意一点，其像和原像必定也处于流形轨道上.本文的算法就是从这一特殊性出发的.

2.1 导数传递

由式（4）、（5）易知，对于任意x∈Ws（x0）（或x∈Wu（x0）），有Fk（x）∈Ws（x0）（或Fk（x）∈Wu（x0））其中k可取任意整数．所以我们可以把稳定流形和不稳定流形的计算当作同一类不变集W来研究.

对于任意x∈W（x0），有F（x）∈W（x0）．对式（1）中的函数F在x处进行Taylor级数展开

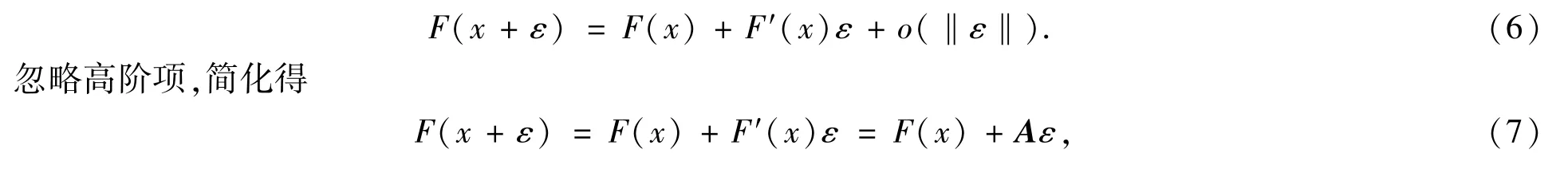
其中A为F在x处的Jacobian矩阵.对于任意n维系统，有

二维状态空间下的情形比较容易理解：Δx2／Δx1可看作是一维流形轨道在x处的斜率，经Jacobian矩阵A变换后得到流形轨道在F（x）处的斜率Δx′2／Δx′1，这就是不变集轨道上的导数传递，高维状态空间下的情况类似［23－24］.

在计算稳定流形的过程中，经常用到的是F－1，为了应用的方便，对F在F－1（x）处进行Taylor级数展开，可得

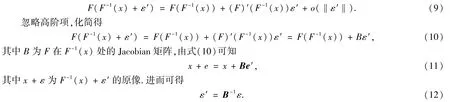
2.2 一维流形计算

以一维不稳定流形的计算为例进行说明.

1）初始化：以不动点x0为起点，沿Eu方向距离为δ处取一点x1，对x1进行映射得到下一点x2＝F（x1），网格点的初始序列为M＝｛x0，x1，x2｝.

2）增长流形.假定当前网格点序列M＝｛x0，…，xn｝，xn＝F（x′n）的原像为x′n，如图1所示，现要在距xn为Δn增加下一点xn＋1，可以通过以下两步来完成：

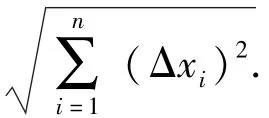
图1 增长流形Fig.1 Manifold extending

b）校正：Δ′n和Δn之间的比值为R＝Δn／Δ′n，然后对ε进行调整，ε＝Rε．由于ε和ε′是线性关系，所以调整之后ε′的模必然为Δn.

xn＋1＝F（x′n＋ε）．之后要检查图1中的夹角α是否满足以下条件

当条件（13）满足时，说明步长Δk合适，则接受xn＋1作为流形上的新点．当α＜αmin时，说明步长过小，但仍然接受xn＋1作为流形轨道上的新点，并设定Δn＋1＝SΔn；当α＞αmax时，则说明步长过大，设定Δn＝Δn／S并重新计算xn＋1．其中S为增长因子，为了保证网格点密度不至于变化太快，建议S的取值范围为1.2＜S＜1.6．此外，当Δn＜Δmin时，为了避免步长过小而影响计算速度，即使条件（13）不满足，也接受xn＋1．与此相对应，当Δn＞Δmax时，则用线性插值插入一个离散点．当流形弧长达到ARC时计算结束.

一维稳定流形的计算方法与此类似，但是由于牵扯到函数的求逆运算，所以还是存在一些差别.现将二者的不同之处列于下表1.

表1 一维稳定和不稳定流形的计算差异Table 1 Differences between algorithm in com puting 1D unstable and stablemanifolds

3 二维流形的计算

二维流形计算在一定意义上就是一族一维流形轨道计算的集合，有了快速的一维流形算法，二维流形的计算就水到渠成了.现在的主要问题是如何确保二维流形在各个方向上的均匀增长.

3.1 推广的Foliation条件

Foliation条件在文献［17］中率先提出，内容如下：在线性Foliation的每个叶形中，与不稳定流形存在唯一的相交线.也就是说，不稳定流形和每个叶形横截相交.

文献［17］应用该条件来确保二维流形在各个方向上的均匀增长.每个叶形定义为与流形环面边界横截相交的一个超平面，该超平面与流形面存在唯一交线.通过选取交线上与流形边界特定距离处的网格点来构成下一个流形环面，二维流形以环面的形式向外增长.Foliation条件通过使流形环面每步向外延伸相同的长度来实现二维流形在各个方向上的均匀增长，由于二维流形与一个平面是拓扑等价的，所以如果将二维流形“展平”，则可以看出，Foliation条件是利用画圆的思想来保证二维流形在各个方向的均匀增长，这个圆的中心为不动点，而圆的半径每步向外增加相同长度.

Foliation条件通过控制环面的扩张来计算二维流形，而二维流形在本质上是由一维流形轨道“铺成”的，所以在实际计算过程中就会产生很多的不便.下面我们将从控制流形轨道的增长速度入手，提出推广的Foliation条件.

首先说明流形轨道上叶形的定义方法：如图2所示，双曲不动点x0的二维局部（不）稳定流形面由两个（不）稳定特征值对应的特征向量V1和V2张成，n＝V1×V2为局部流形面的法向量，对于流形轨道上任意一点xk，由向量和n确定了过点xk的平面，即为该点处的叶形.只要该平面取得足够小，与流形面的交线必定唯一.

推广的Foliation条件内容如下：取流形轨道上任意一点，对该点处的切向分量向该点处的叶形进行投影，沿轨道对投影值进行积分，所得结果就是该流形轨道相对于不动点x0的Foliation弧长.若对二维流形面上的所有流形轨道都计算同样Foliation弧长，就能够保证二维流形在各个方向上的均匀增长.

由于计算过程中流形轨道通常都是用一系列的离散点来表示，是分段线性的，所以Foliation弧长的积分可以用下面的公式来表示.

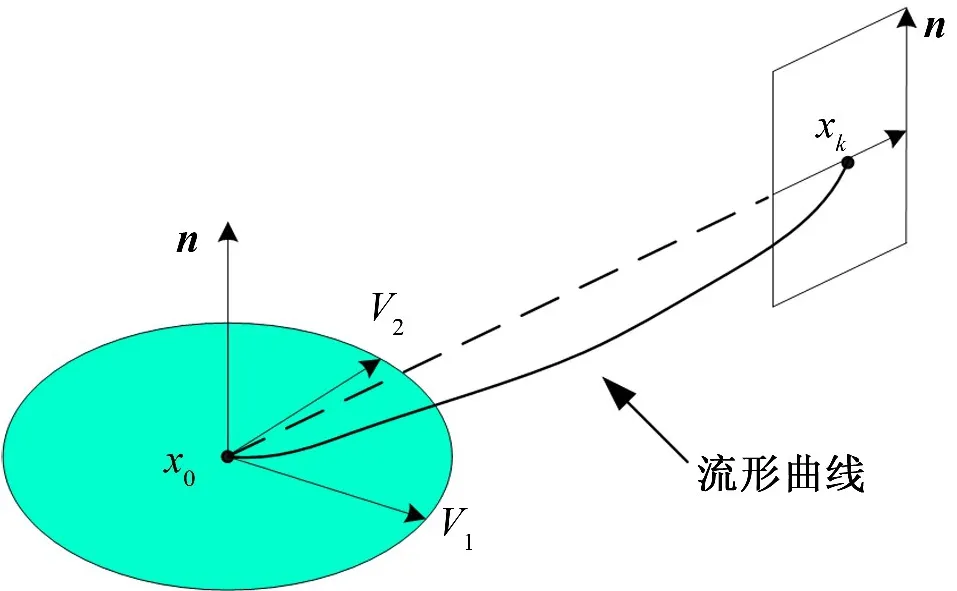
图2 推广的Foliation条件中叶形的定义Fig.2 Definition of linear foliation in generalized Foliation condition

3.2 二维流形计算步骤

以二维不稳定流形的计算为例.由于二维流形实际上就是无穷多条一维子流形的集合，一维流形的计算是二维流形计算的基础，不同于单纯的一维流形计算，在二维流形中计算一维流形轨道时要按照式（14）标出轨道上离散点的Foliation弧长，从而确保二维流形在各个方向上的均匀增长.以不动点x0为圆心，在局部不稳定流形上以δ为半径作圆，在圆上均匀取N个点．然后任取其中一点，与x0相连构成初始流形段，然后按照2.2节所介绍的一维流形计算方法计算出第一条Foliation弧长为ARC的流形轨道L1.

以L1为当前的参考轨道，顺次选取初始圆上的下一点与x0相连构成初始流形段，进行一维流形轨道计算，使Foliation弧长为ARC.然后计算当前轨道上离散点与参考轨道上处于相同Foliation弧长处离散点的距离，若其中某个点对的距离大于网格最大半径SIZEmax，则说明两条轨道间的距离过大，需要在这两条轨道之间再插入一条新的轨道.插入新轨道的方法为：在初始圆上两条轨道的出发点的中点处插入一个网格点，然后以x0和该网格点的连线为初始流形段，计算一条Foliation弧长为ARC的轨道.比较新轨道与参考轨道的距离，若距离仍过大，则按上述方法继续插入新的轨道，否则以新轨道为新的参考轨道，选取初始圆上的下一点进行一维流形轨道计算.

上述过程总的目的是计算出足够多的一维流形轨道来对二维流形面进行覆盖，所以不可避免地会产生冗余，有必要删除一些相互之间距离过小的轨道.仿真过程中发现，一般情况下，相邻轨道最末点之间的距离是两条轨道之间最大的，所以我们以轨道末点之间的距离来代表轨道之间的距离.对于相邻的三条轨道Li、Li＋1、Li＋2，若Li与Li＋1的距离小于网格最小半径SIZEmin，并且Li与Li＋2的距离小于网格最大半径SIZEmax，则删除轨道Li＋1.

接下来就是对计算结果进行可视化.在每条轨道上，抽取Foliation弧长为k×step（k＝1，2，…）处的网格点构成新轨道，其中step规定了网格的大小，可以根据需要进行调整.由于原轨道上的网格点的Foliation弧长不一定恰好满足step的整数倍条件，所以抽取过程中要根据原轨道上网格点的Foliation弧长进行新网格点的线性插值.抽取结束后，依次将各条新轨道上k＝1，2，…，的网格点用线连起来，以流形环的形式表示二维流形，所以同一环上的网格点的Foliation弧长是相同的.可以进一步进行三角形有限元网格化，将二维流形表示为一个曲面，相邻环间的网格化如图3所示，由于相邻环上的网格点是一一对应的，所以操作起来也很方便.

二维稳定流形的计算除了一维流形轨道的计算方法不同，其余操作类似.

图3 流形环之间的三角形网格化Fig.3 Triangulation between two neighboring circles

4 算例分析

仿真硬件环境为AMD phenom三核，2G内存的计算机，使用MATLAB编程.

4.1 三维Hénon映射的二维稳定流形

三维Hénon映射［20］的表达式

当M1＝1.4、M2＝0.2、B＝0.1时，该系统具有混沌吸引子，见图4，这点与著名的二维Hénon映射类似.此时系统的不动点为x0＝（x，y，z），其中x ＝y ＝z＝0.883 9．F 在x0处的Jacobian矩阵为

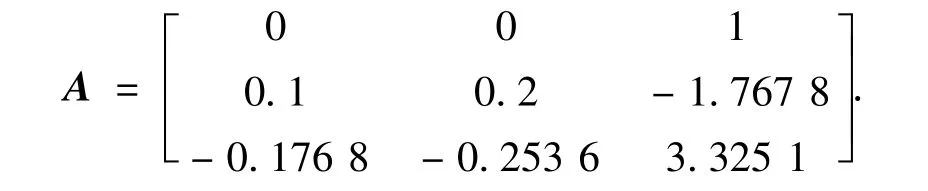
矩阵A的3个特征值的模值分别为：λ1＝3.410 6、λ2＝0.038 6、λ3＝0.075 9，所以x0是一个双曲不动点，且具有一维不稳定流形和二维稳定流形.

计算过程中采用的精度参数如下：δ＝0.1、βmax＝0.15、αmax＝0.15、αmin＝0.05、Δmax＝0.2、Δmin＝0.05、S＝1.4、SIZEmax＝1、SIZEmin＝0.5、step＝0.5．本文采用流形均匀增长的策略，而对于实际流形可能曲率变化不一致，增长步长越小，越能反映局部快速变化的细节，但计算量随之增加，两者是不可调和的矛盾，本文选取的增长步长是兼顾计算速度和计算精度的中间值.

为了说明本文提出的Foliation控制方法能够实现二维流形在各个方向上的均匀增长，先计算一段ARC＝5的二维稳定流形，结果如图5所示.其中不同灰度的环带之间的距离为1，实线为实际计算过程中得到的一维流形轨道，轨道上的点则是抽取的Foliation弧长为step整数倍处的点，容易看出推广的Foliation条件能够很好地保证二维流形在各个方向上的均匀增长.计算图5中的二维流形仅耗时1.25 s.

图4 三维Hénon映射的混沌吸引子Fig.4 Chaotic attractor of 3D Hénon map

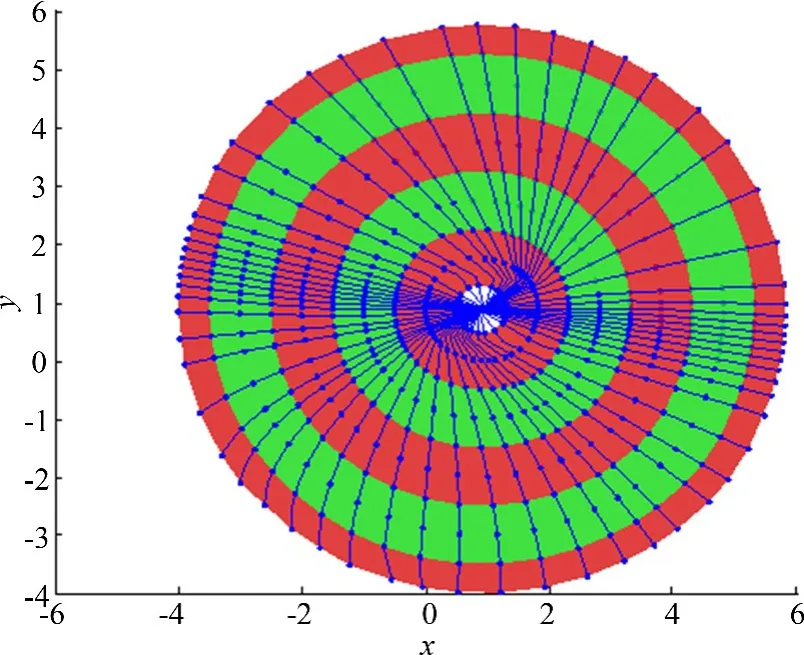
图5 三维Hénon映射二维稳定流形的起始部分Fig.5 Localmanifold of a 3D Hénon map

下面计算ARC＝30的二维稳定流形，结果如图6所示，耗时为108 s.其中不同灰度的环带之间的距离为1.二维稳定流形的形状类似于将一张圆形纸张进行了两次对折.另外，由图可见，当流形的弧长增加时，本文的算法仍然能够很好地控制二维流形在各个方向上的增长速度.

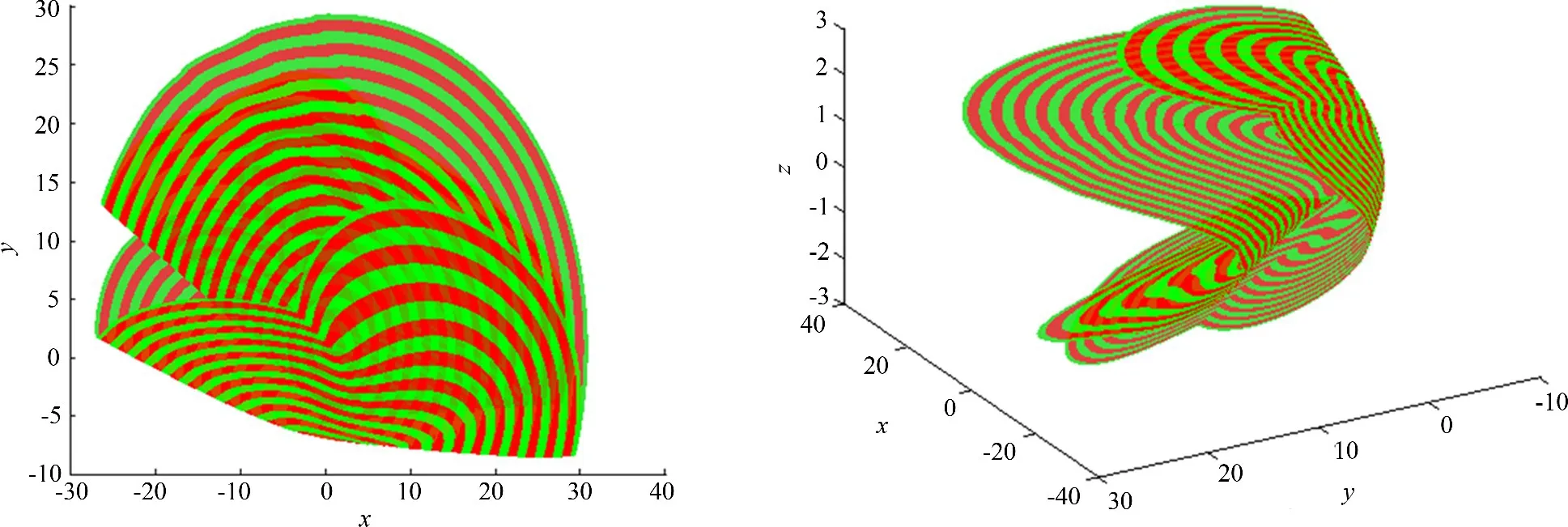
图6 三维Hénon映射的二维稳定流形Fig.6 Stablemanifold of a 3D Hénonmap（ARC＝30）

4.2 Lorenz系统的二维稳定流形

Lorenz系统是一个大气对流模型，以其著名的蝶形混沌吸引子而备受关注.该模型的表达式

当σ＝10、ρ＝28、β＝8／3时，系统的蝶形吸引子如图7（a）所示.该模型是用微分方程表示的，是一个连续系统，我们以差分的形式将其离散化

为了尽可能地保持原系统的性质，需要对采样间隔T进行优化选取．通过实验，发现当T＝0.01时，离散系统具有与原连续系统类似的混沌吸引子（见图7（b）），而且系统的演化速度适中，比较好地保持了原系统的性质.

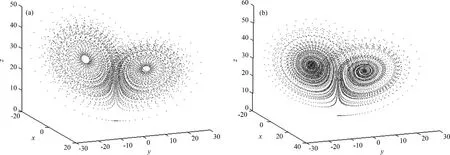
图7 （a）原Lorenz系统混沌吸引子和（b）T＝0.01时，离散化后的Lorenz系统混沌吸引子Fig.7 （a）Chaotic attractor of a continuous Lorenz system；（b）Chaotic attractor of a discrete Lorenz system；

原点是离散化后的Lorenz系统的一个不动点，系统在原点处的Jacobian矩阵为

矩阵A的3个特征值的模值分别为：λ1＝0.771 7、λ2＝1.118 3、λ3＝0.973 3，所以x0是一个双曲不动点，且具有一维不稳定流形和二维稳定流形，这点与原Lorenz系统类似.

计算过程中采用的精度参数如下：ARC ＝80、δ＝0.1、βmax＝0.15、αmax＝0.1、αmin＝0.05、Δmax＝0.1、Δmin＝0.001、S＝1.4、SIZEmax＝1、SIZEmin＝0.5、step＝0.8.

计算结果如图8和图9所示，计算耗时约为22分钟.由图易见本文的算法很好地控制了二维稳定流形在各个方向上的增长速度.该二维稳定流形具有很复杂的几何结构，这也是Lorenz系统复杂动力学性能的一种反映.其中图8以流形环的形式来表示二维稳定流形，不同灰度带之间的距离为5，图9以曲面的形式来表示二维稳定流形，不同灰度带之间的距离为10.

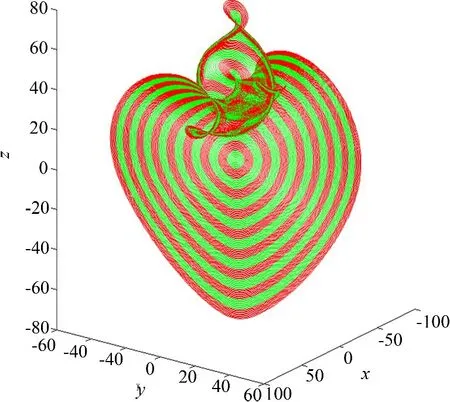
图8 以流形环来表示二维稳定流形Fig.8 Manifold covered by circles

图9 以流形曲面来表示二维稳定流形Fig.9 Manifold covered by circles

图10为系统的一维不稳定流形和二维不稳定流形.其中一维不稳定流形用曲线表示，弧长为1 000，计算耗时为20秒.从图中可以观察到，稳定和不稳定流形除了在原点处相交外，之后二维稳定流形面与蝶形的一维不稳定流形相互缠绕、卷曲，但是始终未相交，这也从一个侧面反映了本文算法的准确性.

5 总结

研究离散动力系统的二维流形计算问题.首先从不变流形沿轨道具有导数传递这个特殊性质出发，提出了一种新的一维流形计算方法，计算过程中以一维流形轨道的切线为参考基准来检查精度，较文献［10］中的控制条件更为简洁，同时能够保证计算的精确性.更为重要的是，本文的算法可以同时用于一维稳定流形和一维不稳定流形的计算.以一维流形计算方法为基础，提出了二维流形计算方法.针对文献［17］中提出的Foliation条件只能应用于流形面的局限，通过对叶形重新进行定义，提出了基于流形轨道的Foliation条件，仿真结果表明，推广的Foliation条件能够很好地控制二维流形在各个方向上的增长速度.文献［17］的算法由于默认新网格点的原像处于已有流形的边界上，所以应用中会有所局限，而本文的方法是以一维流形轨道曲线的计算为基础的，应用中不存在这个限制.相对于文献［18］中的算法，本文显然在均衡二维流形在各个方向的增长速度上更具优势，另外，文献［18］中的算法仅是针对于二维不稳定流形的计算提出的，而本文的算法可以同时计算二维稳定流形和二维不稳定流形，文中的仿真例子说明了这一点，所以本文的算法在适用范围上比文献［18］中的算法更广.

由于本文算法在进行插值时直接从初始环处开始计算轨道，这样就避免了插值点原像的搜索问题，而且插值点之后的轨道也很容易计算，这样做的一个冗余之处在于，会在二维流形上Foliation弧长较短处产生大量的离散点，这也是本文算法以后改进的一个方向.但是值得强调的一点是，对离散动力系统的二维流形进行网格点插值时，需要搜索插值点原像的位置，而这种搜索是在二维流形曲面上进行的，所以操作起来较直接计算轨道更为复杂，这也是本文采取直接计算轨道法的原因.使用本文的方法计算同宿轨道和异宿轨道的前提是必须已知同宿横截点或者异宿横截点以及其对应的增长方向，这是计算同宿轨道和异宿轨道比较困难的问题.

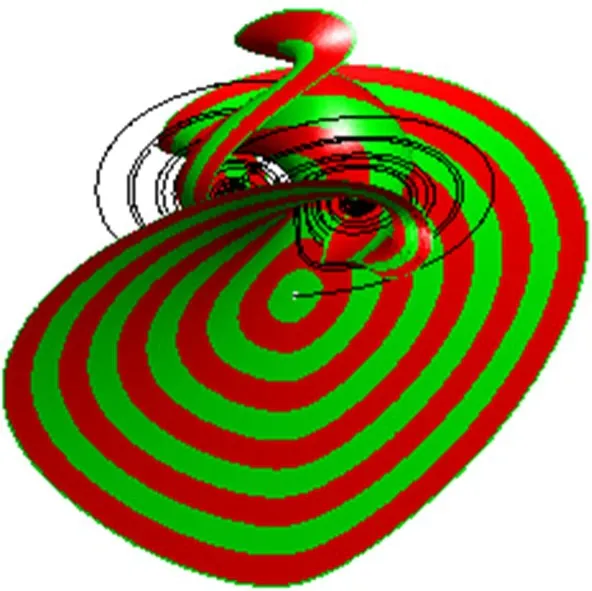
图10 离散化后Lorenz系统的一维不稳定流形和二维稳定流形Fig.10 Stable and unstablemanifold of discrete Lorenz system

［1］Johnson ME，Jolly MS，Kevrekidis IG.Two-dimensional invariantmanifolds and global bifurcations：Some approximation and visualization studies［J］.Numer Algorithms，1997，14：125－140.

［2］Guckenheimer J，Worfolk P，Dynamical systems：Some computational problems［M］.Kluwer Academic Publishers.1993：241－277.

［3］Henderson ME，Siam J.Computing invariantmanifolds by integrating fattened trajectories［J］.Appl Dyn Syst，2005，4：832－882.

［4］Krauskopf B，Osinga H M.Two-dimensional globalmanifolds of vector fields［J］.Chaos，1999，9：768－774.

［5］Krauskopf B，Osinga H M，Doedel E J，Henderson ME，Guckenheimer J，Vladimirsky A，Dellnitz M，Junge O.A survey of methods for computing（un）stablemanifolds of vector fields［J］.Bifur Chaos Appl Sci Engrg，2005，15：763－791.

［6］Guckenheimer J，Vladimirsky A，Siam J.A fastmethod for approximating invariantmanifolds［J］.Appl Dyn Syst，2004，3：232－260.

［7］Li Q D，Yang X S.A new algorithm for computation of two-dimensional unstablemanifolds and its applications［J］.Acta Phys Sin，2010，59（3）：1416－1422.

［8］You Z，Kostelich EJ，Yorke JA，Calculating stable and unstablemanifolds［J］.Int JBifurc Chaos Appl Sci Engrg，1991，1：605－623.

［9］SimóC.On the analytical and numerical approximation of invariantmanifolds［M］∥Benest D，FroeschléC.Les Méthodes modernes de lamécanique céleste goutelas，1989，285－330.

［10］Parker TS，Chua LO.Practical numerical algorithms for chaotic systems［M］.Berlin：Springer，1989：131－140.

［11］Hobson D.An efficientmethod for computing invariantmanifolds［J］.JComput Phys，1991，104：14－22.

［12］Krauskopf B，Osinga H M.Growing unstable manifolds of planar maps［EB／OL］.1997，http：／／www.ima.umn.edu／preprints／OCT97／1517.ps.gz.

［13］Krauskopf B，Osinga H M.Growing 1D and quasi-2D unstablemanifolds ofmaps［J］.JComput Phys，1998，146（1）：406－419.

［14］England JP，Krauskopf B，Osinga H M.Computing one-dimensional stablemanifolds and stable sets of planarmaps without the inverse［J］.Siam JAppl Dyn Syst，2004，3（2）：161－190.

［15］Dellnitz M，Hobmann A.A subdivision algorithm for the computation of unstablemanifolds and global attractors［J］.Numer Math，1997，75：293－317.

［16］Fundinger D.Toward the calculation of higher-dimensional stable manifolds and stable sets for noninvertible and piecewisesmooth maps［J］.JNonlinear Sci，2008，18：391－413.

［17］Krauskopf B，Osinga H M.Globalizing two-dimensional unstablemanifolds ofmaps［J］.Int JBifurc Chaos Appl Sci Engrg，1998，8：483－503.

［18］Li Q D，Zhou L，Zhou HW.Computation for two-dimension unstablemanifold ofmap［J］.Journal of Chongqing University of Posts and Telecommunications（Natural Science Edition），2010，22（3）：339－345.

［19］Palis J，MeloWD.Geometric theory of dynamical systems［M］.New York：Springer-Verlag，1982.

［20］Gonchenko SV，Ovsyannikov II，Simo C，Turaev D.Three-dimensional Hénon-likemaps and wild Lorenz-like attractors［J］. Internat JBifur Chaos Appl Sci Engrg，2005，15（11）：3493－3508.

［21］Li Q D，Yang X S.Computation of two dimensional unstablemanifold［J］.Chinese Journal of Computational Physics，2005，22（6）：549－554.

［22］Timothy JH，Li Q D，Cheng R B.Wrinkling behavior of highly stretched rectangular elastic films via parametric global bifurcation［J］.Journal of Nonlinear Science，2013，23：777－805.

［23］Sun H，Fan Y，Li H，et al.Computation of two-dimensional invariant manifolds with radial growth factor［J］.Chinese J Comput Phys，2011，28（4）：621－625.

［24］Li H，Fan Y，Zhang J.Computing stable and unstablemanifolds of typical chaoticmaps［J］.Chinese JComput Phys，2011，28（6）：927－932.

Grow ing 2D Manifold of Discrete Dynam ical System Based on Foliation Condition

JIA Meng
（Department of Electrical Engineering，Xinxiang College，Xinxiang 453003，China）

An algorithm for computing 2D stable and unstablemanifolds of hyperbolic fixed points of discrete dynamical systems is shown.With the fact that Jacobian transports derivative along orbitof an invariantmanifold，an algorithm for computing 1Dmanifold is proposed.Themesh point is located with a Prediction-Correction schemewhich reduces searching time and at the same time gives rise to a simplified accuracy condition.2D manifold is computed by covering it with orbits of 1D sub-manifold.A generalized Foliation condition is used to guarantee that2D manifold is growing equally along orbits of 1D sub-manifold in different directions.Performance of the algorithm is demonstrated with hyper chaotic 3D Hénonmap and Lorenz system.

discrete dynamical system；stable manifold；unstable manifold；derivative transportation；3D Hénon map；Lorenz system；chaotic attractor

date：2013－07－22；Revised date：2013－11－26

O59

A

1001-246X（2014）04-0495-10

2013－07－22；

2013－11－26

河南省重大科技攻关项目（112102210014）资助

贾蒙（1981－），男，河南新乡，博士，从事非线性流形计算和非线性信号处理研究，E-mail：tianshi_cd＠163.com