天然裂缝储层压裂定向井稳态产量的蒙特卡洛计算

张 晋， 黄世军， 程林松

（中国石油大学（北京）石油工程学院，北京 102249）

天然裂缝储层压裂定向井稳态产量的蒙特卡洛计算

张 晋， 黄世军， 程林松

（中国石油大学（北京）石油工程学院，北京 102249）

针对各向异性天然裂缝储层，蒙特卡洛随机模拟天然裂缝分布，从统计学角度表征天然裂缝参数，根据势叠加原理，把天然裂缝和人工裂缝当成独立的源进行势叠加，考虑天然裂缝和人工裂缝的耦合作用，建立压裂定向井稳态产量计算公式.计算结果表明，基于蒙特卡洛的天然裂缝模拟能从统计学角度反映产量变化趋势，能快速分析压裂定向井稳态产能.

天然裂缝；定向井；压裂；产量计算；蒙特卡洛

0 引言

随着油气资源开发难度的加大，低渗透油气藏已成为油气田开发的主要对象.水力压裂能增大泄流面积，沟通天然裂缝形成缝网，进一步增加产量，已经成为低渗透油藏开发的常规工艺［1－2］.对于海上低渗透油藏丛式井，受经济和技术因素的限制，多为压裂大斜度井.关于天然裂缝性油藏的研究，Warren和Root［3］建立双重介质理论模型，Kazemi［4－5］、Sonier［6］等人在此基础上将模型扩展到二维和三维流动，模拟了全区油藏实际模型.Baca等［7］，Kim和Deo［8］，Karimi Fard和Firoozabadi［9］，黄朝琴［10］等基于有限元方法发展了离散网络模型，相比于双重介质模型能更精确描绘每条裂缝.双重介质模型和离散网络模型均能良好的模拟常规天然裂缝，但是对于低渗透油藏压裂后形成复杂裂缝的情况处理困难，精度有限.冯金德等［11］运用等值渗流阻力法处理天然裂缝，建立了裂缝性低渗透油藏稳态渗流的理论模型.程林松等［12］根据裂缝性油藏水平井渗流特征，建立了考虑天然裂缝和水平井生产段共同渗流的耦合模型.Qin G等［13］通过蒙特卡洛方法模拟分析了体积改造（SRV）的产能规律，这三个模型均能有效分析天然裂缝储层产能规律，但对于定向井压裂成倾斜裂缝，无法处理.对于天然裂缝地层，定向井（斜井）压裂产能及增产机理仍没有一个系统完善的研究，因此从理论上研究天然裂缝储层中定向井压裂产能对大斜度压裂丛式井的开发具有指导意义.

1 天然裂缝的模拟

在漫长的地质年代中，构造运动、卸载作用和内部流体作用等使得岩体内部和表面产生大量各种类型的不连续结构面，即天然裂缝.实践中可以通过仪器测量了解天然裂缝的分布和形态特征，但是这样费时费力、成本高且难以识别更微小的裂隙情况.随着计算机技术的发展，逐渐发展用计算机表征天然裂缝的形态，包括整体的裂隙分布情况和裂隙面的凹凸情况等.

根据已有的岩体裂隙研究成果以及地质工程实践可知［14］，岩体裂隙的几何要素一般都具有统计规律，服从某一种或几种类型的概率分布.一般来说，裂隙的条数依据其密度服从Poisson随机过程；裂隙中心点位置服从研究域内的均匀分布；产状（走向和倾角）通常服从Bingham分布、单变量或双变量Fisher分布、双变量正态分布或对数正态分布、均匀分布等；迹长（半径）和隙宽服从负指数分布或对数正态分布.

蒙特卡洛原理是通过对模型和过程的观察或者抽样试验来计算所求参数的统计特征，从而解决工程等方面的实际问题.对于蒙特卡洛模拟，首先是要构造和描述概率过程.蒙特卡洛模拟基于各种概率分布的随机变量，其中最重要的随机变量是［0，1］随机分布，其他分布的抽样都是借助它来实现.计算机上产生随机数是通过迭代产生的，其结果不是随机的，但是迭代过程开始前每一项都不能预知，大量这样的数能够通过局部随机性检验就可以作为随机数来使用，即伪随机数.这样的方法借助于迭代公式，速度快、费用低廉［15］.其次，根据天然裂缝统计数据回归出概率分布的参数，将天然裂缝半径、位置、数量、倾角和走向用随机函数表征，通过计算机产生一定分布的随机数，从而实现天然裂缝的模拟.

国内外裂隙表征模型有三大类：力学模型，几何模型和几何力学模型.为了能方便计算产能，运用Baecher圆盘模型［16］，裂缝半长，空间位置，产状，裂缝密度（条数）各自服从一定的概率分布.根据统计天然裂缝的数据，回归出各参数服从的概率分布参数，然后根据蒙特卡洛随机模拟出天然裂缝的参数和分布位置.

假设某区块天然裂缝的密度（条数）服从泊松分布，裂缝半径服从对数正态分布，产状（倾角和走向）服从双变量正态分布，天然裂缝圆盘中心坐标服从均匀分布.蒙特卡洛随机模拟两种产状情况下天然裂缝分布结果如图1所示.

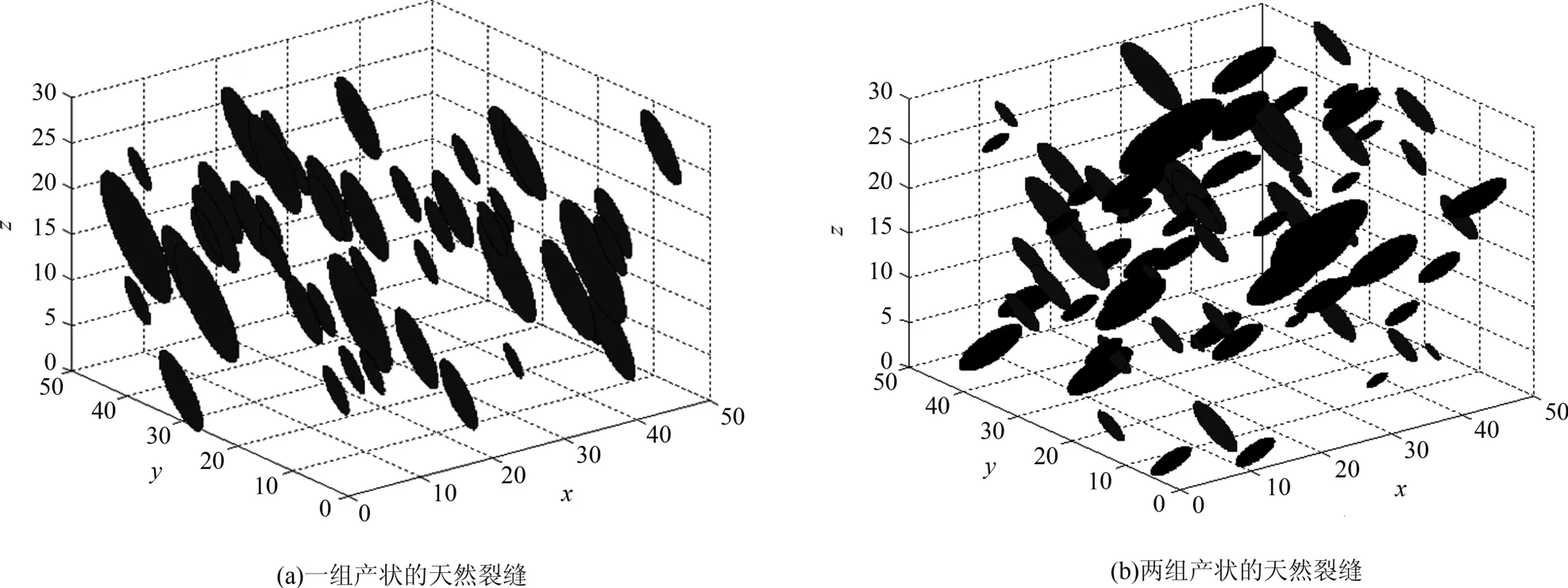
图1 天然裂缝模拟图Fig.1 Simulation of natural fractures

2 天然裂缝储层压裂定向井产量模型

2.1 压裂定向井势函数

室内真三轴模拟压裂实验发现定向井水力压裂裂缝起裂及扩展的一些规律［17］：当定向井方位沿最大水平主应力方向，裂缝沿最大水平主应力方向起裂，且不发生偏转；当定向井沿最小水平主应力方向，发生裂缝转向；裂缝转向后仍会沿最大主应力方向扩展.

为简化模型，便于推导，将裂缝简化成沿井筒的平面，裂缝沿最大主应力方向延伸.其假设为：①油藏为均质、等厚各向异性无限大地层，其中各向异性渗透率Kx＝Ky＝Kh，Kz＝Kv；②单相不可压缩流体，油藏中渗流符合达西定律；③在任意x-y平面上，压裂裂缝总是沿最大水平主应力方向延伸（设为x方向）；④忽略重力和井筒沿程压力损失的影响；⑤忽略裂缝内的流动，流体流到裂缝即当作流入了井筒；⑥裂缝段井筒为生产段，裂缝为倾斜缝；⑦井筒简化成直线，裂缝简化成平面；

根据势叠加［18－20］，整个裂缝面在无限大地层中任意点M（x，y，z′）所产生的势为

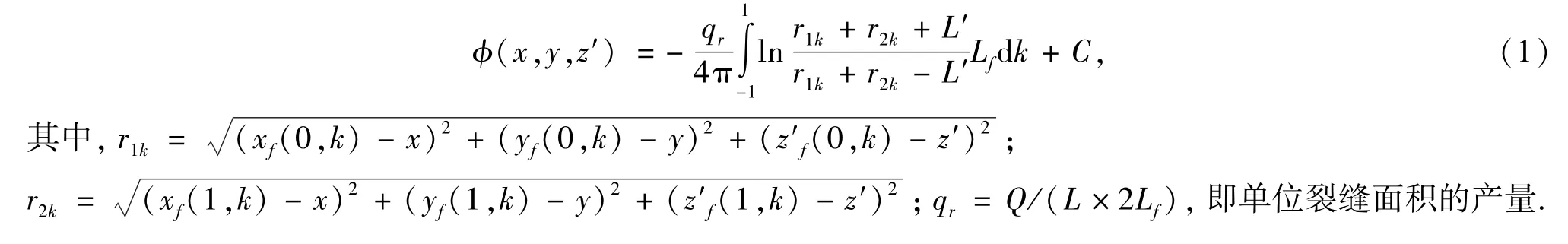
2.2 天然裂缝势函数

含天然裂缝的储藏，水力压裂后产生非常复杂的裂缝网络，将三维面势叠加模型运用于水力压裂裂缝／天然裂缝系统，为简化物理模型，假设天然裂缝连接主裂缝，流体从储藏流入天然裂缝后流入主裂缝；对于人工压裂的主裂缝，流体来自储藏和连接的天然裂缝，然后主裂缝中流体流入井筒.对于未与人工裂缝连接的天然裂缝，当成孤立裂缝，不影响压裂定向井产能［21］.每个水力压裂裂缝和天然裂缝是彼此相互独立的源，运用叠加原理可计算压力和产量.

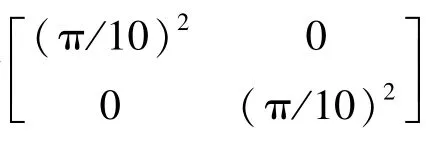
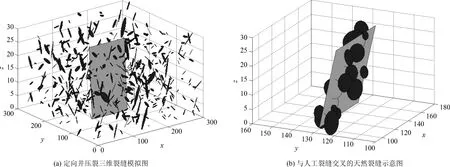
图2 天然裂缝与人工裂缝耦合图Fig.2 Coupled natural and artificial fractures

设计算法，将与人工裂缝交叉的天然裂缝选出来，如图2（b），只有这部分的天然裂缝与人工裂缝沟通，流体可以通过这部分的天然裂缝流入人工裂缝，最终流入井筒，而空间中其他天然裂缝则为孤立裂缝，文中忽略这部分的裂缝对产能的影响.与人工裂缝交叉的天然裂缝可以作为单独的源与人工裂缝一起进行势叠加，计算圆盘的势.

对于圆盘做势叠加，其势函数为

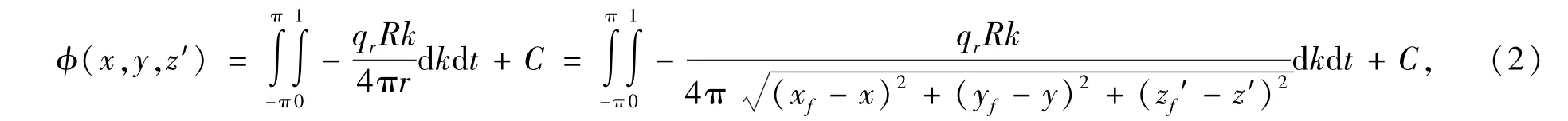
式中有，xf＝Rkcosθ cost cosα＋Rksint sinα＋x0；yf＝－Rkcosθ cost sinα＋Rksint cosα＋y0；zf＝Rkcost sinθ＋z0．其中－π≤t≤π，0≤k≤1，（x0，y0，z0）为圆盘的圆心坐标，（xf，yf，zf）为天然裂缝上任意点的坐标，θ为圆盘天然裂缝的倾角，α为圆盘天然裂缝的走向，R为圆盘裂缝的迹长即半径.

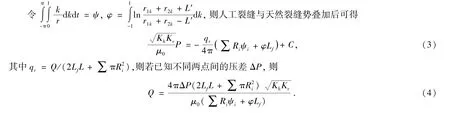
3 模型验证与敏感性分析

采用某油田的油藏参数（如表1所示），根据概率分布参数，随机模拟天然裂缝，通过与人工裂缝一起进行势叠加，从而计算各自产量以及总产量.10次随机模拟取产量平均数，如图3所示.

用式（1）计算该压裂定向井产量（即不考虑天然裂缝），得产量为4.68 m3·d－1，现场数据中缺乏对天然裂缝的统计，用假设的天然裂缝参数随机模拟计算，得产量为6.77 m3·d－1，实际产量为6.1 m3· d－1，与蒙特卡洛随机模拟结果接近.（1）式忽略了天然裂缝的贡献，计算产量偏小，蒙特卡洛法假设裂缝无限导流，计算产量偏高，蒙特卡洛法计算结果与实际值更为接近.此外，蒙特卡洛模型中误差也来源于天然裂缝统计，并存在一定的随机性.

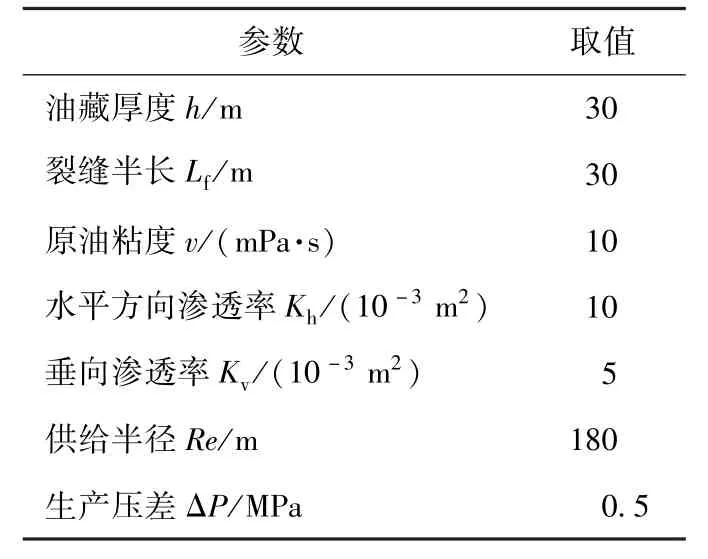
表1 油藏参数Table 1 Reservoir parameters

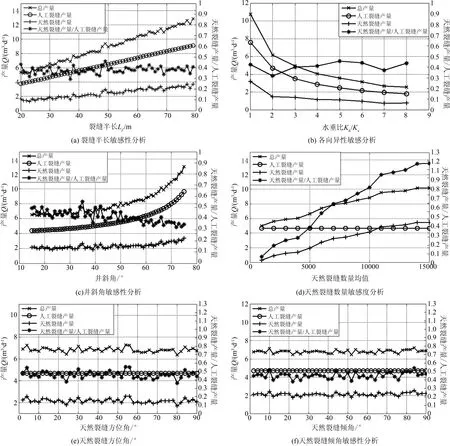
图3 产量敏感性分析图Fig.3 Analysis of production sensitivity

如图3（a）所示，随着裂缝半长的增加，人工裂缝产量呈直线上升趋势，天然裂缝产量和总产量由于模拟的随机性，呈波动直线上升趋势，天然裂缝与人工裂缝对产能贡献比值在0.4左右波动，没有明显的变化趋势.这是因为随着裂缝半长的增加，人工裂缝泄油面积增加，与人工裂缝相交的天然裂缝数量也线性增长，模型假设中天然裂缝和人工裂缝均作为独立的源进行势叠加，所以两者产量上升而比值不变.

如图3（b）所示，随着渗透率非均质性程度增加，人工裂缝产量，天然裂缝产量和总产量均呈下降趋势，且当非均质性较弱时产量下降快，天然裂缝与人工裂缝对产能贡献比值在0.4左右波动，无明显变化趋势.这说明储层各向异性对人工裂缝和天然裂缝产量影响很大，各向异性越强产量越低.模型假设中天然裂缝和人工裂缝均作为相同的源进行势叠加，所以两者产量下降而比值不变.

如图3（c）所示，随着井斜角的增加，人工裂缝产量，天然裂缝产量和总产量均呈上升趋势，且人工裂缝产量上升比天然裂缝快，天然裂缝贡献比重有小幅下降趋势.这是因为井斜角增加使得人工裂缝面积越大，势函数越大，产量越高，而人工裂缝面积越大，则与人工裂缝交叉的天然裂缝数量越多，天然裂缝产量也越大，但是人工裂缝产量增加更多，因此天然裂缝与人工裂缝产量比重有所下降.

如图3（d）所示，随着天然裂缝数量的增加，天然裂缝产量急剧上升，在300 m×300 m×30 m范围内天然裂缝数量达到12 000条左右时，天然裂缝贡献产能部分超过了人工裂缝.如图3（f）和图3（g）所示，天然裂缝走向和倾角对产量影响不大，这是因为随着走向的变化，天然裂缝与人工裂缝相交的概率并没有随之增加.

4 结论

天然裂缝对产能的贡献不可忽略，分析复杂裂缝网络对产能的影响后可得到以下结论：

1）通过蒙特卡洛随机模拟天然裂缝储层，从统计规律角度表征天然裂缝具有实际意义.

2）通过计算机随机模拟的方式分析天然裂缝储层稳态产量不仅经济而且省时，人工裂缝与天然裂缝耦合，能快速分析压裂定向井稳态产能.

3）天然裂缝储层压裂定向井产能影响因素中，天然裂缝密度是最重要的影响因素.压裂及井身设计时，为提高产量，可在经济允许条件下增大裂缝半长和井斜角.

［1］Zeng F，Guo J，Xu Y，et al.Factors affecting production capacity of fractured horizontal wells［J］.Petroleum Exploration and Development，2007，34（4）：474－477.

［2］Xu F，Yang J，Hu X，et al.Puzzlers of horizontal well technique in low permeability reservoir［J］.Special Oil＆Gas Reservoirs，2001，8（4）：36－39.

［3］Warren J E，Root P J.The behavior of naturally fractured reservoirs［J］.Old SPE Journal，1963，3（3）：245－255.

［4］Kazemi H.A pressure transient analysis of naturally fractured reservoirs with uniform fracture distribution［J］.Old SPE Journal，1969，9（4）：451－462.

［5］Kazemi H，LS M，Porterfield K L，et al.Numerical simulation of water-oil flow in naturally fractured reservoirs［J］.Old SPE Journal，1976，16（6）：317－326.

［6］Sonier F，Souillard P，Blaskovich F T.Numerical simulation of naturally fractured reservoirs［J］.SPE Reservoir Engineering，1988，3（4）：1114－1122.

［7］Baca R G，Arnett R C，Langford D W.Modelling fluid flow in fractured-porous rock masses by finite-element techniques［J］. International Journal for Numerical Methods in Fluids，1984，4（4）：337－348.

［8］Kim J G，Deo M D.Finite element，discrete-fracture model for multiphase flow in porous media［J］.AIChE Journal，2000，46（6）：1120－1130.

［9］Karimi－Fard M，Durlofsky L J，Aziz K.An efficient discrete-fracture model applicable for general-purpose reservoir simulators［J］.SPE Journal，2004，9（2）：227－236.

［10］Huang Z，Yao J，Wang Y，et al.Numerical simulation on water flooding development of fractured reservoirs in a discretefracture model［J］.Chinese Journal of Computational Physics，2011，28（1）：41－49.

［11］Feng J，Cheng L，Li C.A theoretical model of steady-state flow for naturally fractured low-permeability reservoir［J］.XinjiangPetroleum Geology，2006，27（3）：316－318.

［12］Cheng L，Pi J，Lian P，et al.A computational method for productivity of horizontal well in naturally fractured reservoirs［J］. Chinese Journal of Computational Physics，2011，28（2）：230－236.

［13］Qin G，Chen R，Gong B，et al.Data-driven Monte Carlo simulations in estimating the stimulated reservoir volume（SRV）by hydraulic fracturing treatments［C］∥SPE Europec／EAGE Annual Conference，2012.

［14］Liu X，Wang E，Wang S，et al.Representation method of fractured rock mass and its hydraulic properties study［J］.Chinese Journal of Rock Mechanics and Engineering，2008，27（9）：1814－1821.

［15］Jin C.Study on random number generator and random sampling in Monte Carlo method［D］.Dalian：Dalian University of Technology，2005.

［16］Baecher G B，Lanney N A，Einstein H H.Statistical description of rock properties and sampling［C］∥The 18th US Symposium on Rock Mechanics（USRMS），1977.

［17］Wang L.Research on prolongation law of hydraulic fracture for directional well［D］.Dongying：China University of Petroleum （East China），2011.

［18］Chen Y，Yan T，Bi X.Theoretical research on 3-D potential distribution in reservoir of inclined well when considering borehole pressure drop［J］.Drilling＆Production Technology，2002，25（5）：17－19.

［19］Huang S，Cheng L，Zhao F，et al.Production evaluation model of a fishbone well considering coupling among multi-segment flows［J］.Journal of China University of Petroleum（Natural Science Edition），2010，34（2）：83－88.

［20］Lian P，Cheng L，Cao R，et al.A coupling model of low permeability reservoir and fractured horizontal wellbore in nonsteady state［J］.Chinese Journal of Computational Physics，2010，27（2）：203－210.

［21］Lin J，Zhu D.Predicting well performance in complex fracture systems by slab source method［C］∥SPE Hydraulic Fracturing Technology Conference，2012.

Monte Carlo Calculation of Stable Productivity of Fractured Directional Wells in Natural Fracture Reservoirs

ZHANG Jin，HUANG Shijun，CHENG Linsong
（College of Petroleum Engineering，China University of Petroleum（Beijing），Beijing 102249，China）

We focus on anisotropic reservoir with natural fractures，and simulate distribution of natural fracture with Monte Carlo.It characterizes natural fracture parameters from the perspective of statistics.Coupled natural and artificial fractures are considered as independent sources.A formula of steady production is derived according to potential superposition principle.It shows that Monte Carlo simulations of natural fractures reflect trends of productivity from a statistical point of view.It analyzes quickly steady productivity of fractured directional well.

natural fracture；directional well；fracture；productivity calculation；Monte Carlo

date：2013－10－11；Revised date：2014－01－27

TE319

A

2013－10－11；

2014－01－27

国家自然科学基金（51174215／E0403）资助项目

张晋（1990－），男，湖南湘乡人，硕士生，主要从事油气田开发与渗流机理研究，E-mail：zhangjin_1990＠foxmail.com

1001-246X（2014）05-0567-06