采用态－态模型的热化学非平衡喷管流数值研究

徐 丹， 曾 明， 张 威， 柳 军

（国防科学技术大学航天科学与工程学院，湖南长沙 410073）

采用态－态模型的热化学非平衡喷管流数值研究

徐 丹， 曾 明， 张 威， 柳 军

（国防科学技术大学航天科学与工程学院，湖南长沙 410073）

数值求解耦合态－态模型的N2／N准一维喷管非平衡流方程，获得驻室温度3000 K～10000 K，压力1 atm～10 atm条件下的流场参数分布和详细的振动能级分布，分析喷管流动中的宏观和微观特性，并对这类复合占优的流动考察双温度模型中假设的合理性.

态－态模型；热化学非平衡；振动能级分布；高超声速喷管流动；数值模拟

0 引言

高超声速高焓流动中常同时存在热力和化学非平衡现象.对热力非平衡流动，气体各种模式的内能无法用统一的温度表征.一般而言，转动与平动内能模式较易达到平衡，可以用同一温度描述，记作平动／转动温度或平动温度T，且平动和转动能级分布为该温度下的Boltzmann分布.在电子能可以忽略的情况下，热力非平衡主要表现为振动非平衡.有两类描述流动中热力非平衡现象和热力－化学耦合的方法.一类是多温度模型法，以双温度模型法［1］为代表，通过振动能变化率方程描述振动非平衡过程，以不同于平动温度的振动温度Tv表征非平衡振动能，将化学反应控制温度设为平动温度与振动温度的某种平均值以反映热力－化学耦合；另一类是态－态模型法［2－3］，直接描述分子在各振动能级间的非平衡跃迁过程，给出各能级粒子数变化率方程，热力－化学耦合则通过分别描述各能级上分子的化学反应过程自然体现.

双温度模型法引入振动能变化率方程和流动控制方程耦合求解，得到流场各点的非平衡振动能后借用平衡振动能和温度的关系式，折算出振动温度Tv，它与平动温度的差别能直观地反映流动中的振动非平衡现象.振动温度进入化学反应控制温度也是一个简便地体现热力－化学耦合的方法.双温度模型及其后来拓展的多温度模型一定程度上反映了流动中的热力非平衡现象和热力－化学耦合，在高温非平衡流的数值模拟中获得了广泛的应用，在许多条件下也获得了良好的数值结果，但是也存在局限［4］，例如在复合区的效果不如离解区，无法合理解释AVCO实验数据，等.其实化学反应控制温度（即化学反应速率系数Arrhenius公式中的温度）中包含振动温度的内涵是值得进一步分析的.Arrhenius速率系数公式中的温度参数一方面是反映粒子碰撞频率，与随机热运动（平动）速度有关；另一方面则是反映碰撞能够引起化学反应的概率，与参与碰撞粒子的内能（包括平动、转动、振动、电子能）有关，这里以温度反映粒子内能的物理内涵其实是基于参与反应的粒子能级分布满足该温度下的平衡分布（Boltzmann分布）的.因此从这个角度看，在化学反应控制温度中引入振动温度，可以说隐含着对振动非平衡流采用了振动能级分布满足振动温度下Boltzmann分布的假设，这个假设是否合理，需要进一步研究.另外，采用何种方式对平动温度和振动温度取平均以确定化学反应控制温度主要依据经验，也具有相当的不确定性.

态－态模型法描述振动非平衡及其与化学反应耦合的方法则更为精细和直接.它将粒子在能级间的跃迁与化学反应视为同一性质的过程研究，能够得到流体组元详细能级分布而不只是总的非平衡振动能的变化规律，掌握了更多的细节；它直接研究各能级上粒子的化学反应，避免了多温度模型中经验性的热力－化学耦合方法.不过，尽管态－态模型在理论上展现出诸多优点，但各种内能模式能级间的跃迁过程复杂，使得计算中处理的信息量巨大，并且计算结果强烈依赖于所使用的微观模型和动力学给出的相关数据，所以目前还无法实现态－态模型与多维流场程序的耦合［5］，国外采用态－态模型的研究一般集中在不涉及流动的零维问题［5］，或是正激波后、边界层［6－7］和准一维喷管非平衡流动［8－9］问题.

国内在态－态模型的研究方面刚刚起步，一些学者对模型基本原理和实验方法进行了总结和讨论［10］，笔者曾采用态－态模型研究零维问题［11］，对等温等压或等温等容的N2／N混合物系统，详细研究其热化学非平衡过程，揭示了非平衡过程中的一些微观分布信息，加深了对态－态模型和非平衡过程的理解.

进一步将态－态模型与流动耦合，研究N2／N混合物的准一维热化学非平衡喷管流动.国外学者求解耦合态－态模型的准一维非平衡喷管流控制方程时是采用空间推进方法［8－9］，考虑到非平衡喷管流中喉部非声速等原因造成的入口条件试凑的困难，本文采用时间推进法.在驻室温度3 000 K～10 000 K，压力1 atm～10 atm条件下数值求解N2／N非平衡喷管流动，获得流场参数分布特别是详细的振动能级分布，分析喷管流动中的宏观和微观特性变化特点.对这类复合占优的流动，考察双温度模型中假设的合理性.

1 基本方程与计算方法

态－态模型将位于不同振动能级上的分子视为不同组元，位于振动能级v上的N2记作N2（v）.本文采用有68（0～67）个振动能级的N2能级模型，因此N2（v）／N混合物中含68个分子组元和1个N原子组元，共69个组元.态－态模型直接描述分子在不同振动能级间的跃迁和各能级上分子N2（v）与原子N的化学反应，共5类过程：分子间的振动－平动能量交换过程（vTm）、分子与原子间的振动－平动能量交换过程（vTa）、振动－振动能量交换过程（vv）；原子作为碰撞参与者的离解－复合反应（dra）和分子作为碰撞参与者的离解－复合反应（drm）.具体表示如下［12］

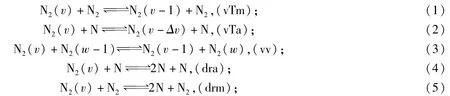
其中v和w代表N2的不同振动能级.根据上述各类跃迁或化学反应的速率方程就可给出N2（v）和N共计69个组元的质量生成率.各类过程的速率系数具体计算公式和相关数据见文献［6，12－13］.

对非平衡流动，需要69个组元连续方程.加上动量、能量方程后，守恒形式的准一维热化学非平衡喷管流控制方程为

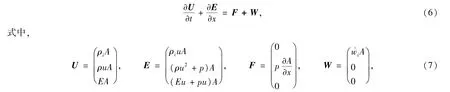
其中ρi为N2（v）和N各组元的密度，A为喷管截面面积，E为单位体积的总能，˙wi为的各组元的质量生成率，由上述（1）～（5）式给出的各类过程的速率方程表达，其中包含各组元密度ρi．

对控制方程（6）式进行差分离散时，无粘通量项E和源项W采用全隐格式，右端项F采用显式离散，隐式求解方法为LU-SGS方法，具体参见文献［14］.源项隐式求解时需要的（∂W／∂U）矩阵需根据态－态模型各跃迁过程的速率系数公式推导计算［15］.

定解条件中，喷管入口给出总温总压条件，流速由内点外插得到，假设驻室至入口第一点流动接近平衡因而等熵.入口点的N原子和各振动能级N2（v）的质量分数采用驻室温度压力下的态－态模型平衡结果给定.喷管超声速出口边界上所有物理量由内点外插得到.初场的确定首先根据喷管各点膨胀比分布马赫数，以热化学平衡条件给出对应马赫数的宏观流动参数，N和N2（v）组元的质量分数则取为驻室条件下的态－态模型的平衡结果.

为验证笔者编制的“态－态模型”数值计算程序，曾对文献［12］的算例，进行了N2／N系统热化学非平衡过程的数值模拟，程序结果和文献结果吻合很好［11］.

2 数值算例与结果分析

喷管流动计算针对一轴对称的喷管进行.喷管半径沿轴线的分布曲线为抛物线

喷管长度为1 m，喉部位置在x＝0.5 m处.

喷管驻室温度T0在3 000 K～10 000 K范围，驻室压力p0在1 atm～10 atm范围，本文选取了多个算例条件求解N2／N非平衡喷管流场，下面以T0＝8 000 K（N2离解程度较高）和T0＝3 000 K（离解程度很低）两组算例为代表给出数值计算结果和分析.

2.1 T0＝8 000 K算例

采用了态－态模型进行喷管非平衡流计算得到的宏观流动参数如压力、温度、密度、速度在气流膨胀过程中的变化特点与双温度模型得到的结果一致，这里不再给出，下面主要讨论组元质量分数或N2（v）与N2的粒子数之比沿轴线的分布，喷管中不同位置的振动能级分布及其偏离Boltzmann分布的特点.

2.1.1 参数沿轴线分布

图1给出了N质量分数CN沿喷管轴线的分布.p0＝1 atm条件下CN约在0.7～0.8之间，5 atm时约为0.4～0.5，10 atm时约为0.3～0.4.这是总压升高抑制驻室N2离解，而膨胀过程中提高压力又促进N复合生成N2的缘故.三个总压条件下喷管喉道下游都表现出化学冻结的现象，但总压越大，冻结出现得越晚.

图2以第0（基态）和第30振动能级为代表给出了N2（v）质量分数CN2（v）沿轴线的分布.各振动能级N2（v）的质量分数在入口到x／L＝0.4这段范围内变化都较小，直到喉道附近才发生明显变化，最后在喉道下游的不同位置趋于冻结.喉道前温度变化较小，各能级的CN2（v）也相对稳定，到喉道附近后温度快速降低，CN2（v）发生明显变化.喉道下游气流膨胀过程中温度继续下降，但由于压力和密度的快速下降，各类跃迁和化学反应速率都急剧下降，而流速又快速增大，因此喉道下游不远处就表现出流动热化学冻结的特点.不同振动能级出现冻结的位置略有差别，但大致都在x／L＝0.6～0.8之间.总压越高流动冻结出现得越晚，这是由于压力增加（密度增大）增大了粒子碰撞频率，使流动的非平衡程度降低.振动基态的CN2（0）在膨胀过程中随温度降低而增加（见图2（a）），而其它较高振动能级的CN2（v）变化趋势相反（见图2（b））.从CN2（v）冻结值来看，总压越大，基态及低能级的冻结值越高，而高能级的冻结值越低，这与总压升高推迟流动冻结的特点是一致的.

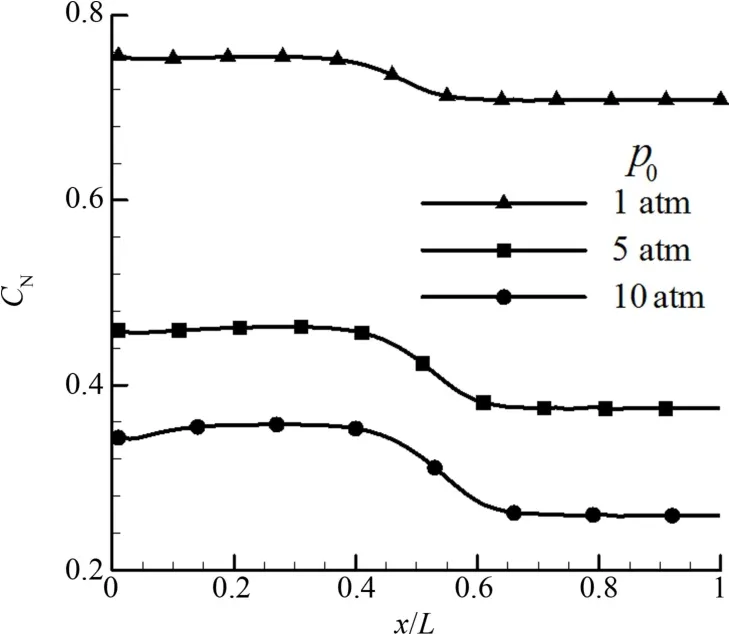
图1 T0＝8 000 K条件下CN沿喷管轴线分布Fig.1 Distribution of CNalong the axis of nozzle at T0＝8 000 K

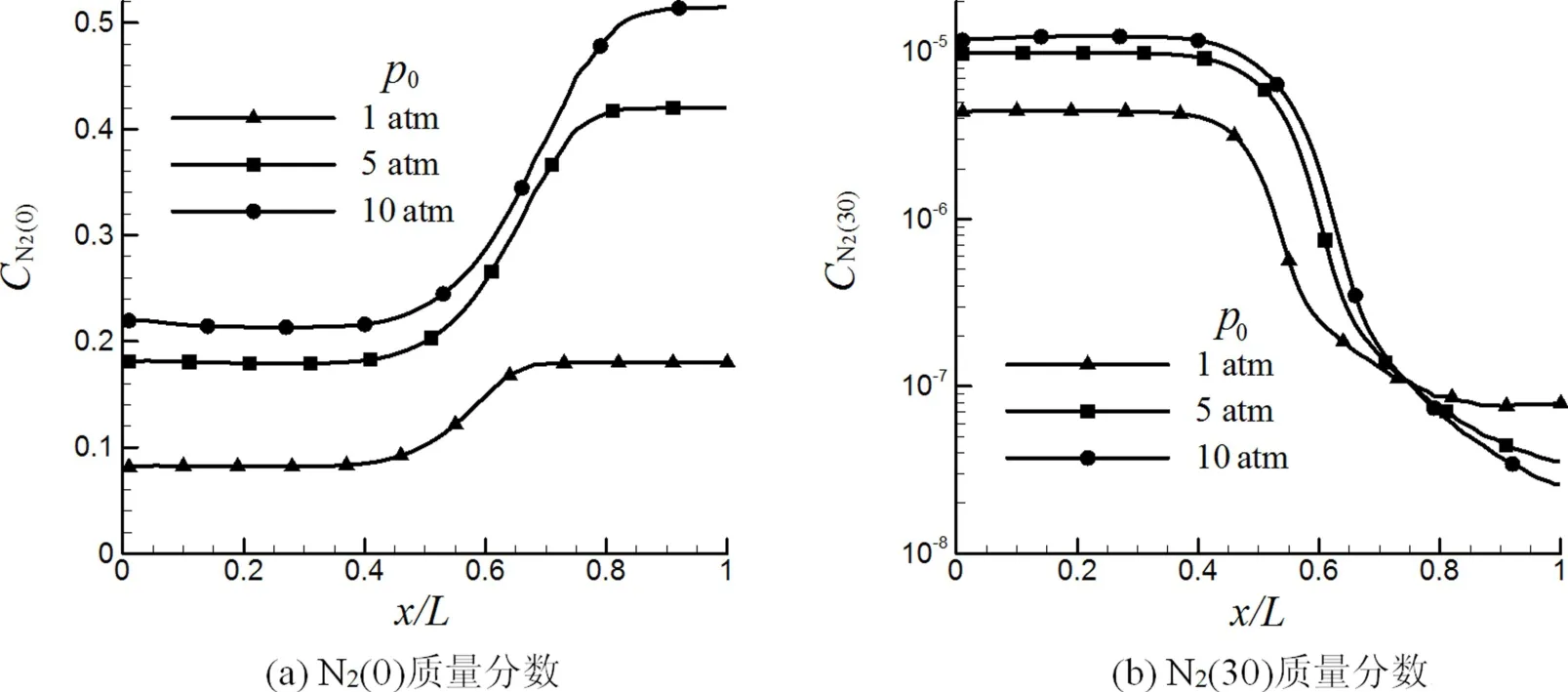
图2 T0＝8 000 K条件下CN2（v）沿喷管轴线分布Fig.2 Distribution of CN2（v）along the axis of nozzle at T0＝8 000 K

图2反映了总压条件对CN2（v）在膨胀过程中变化规律的影响，但由于不同总压条件下N2／N混合物的组成不同，质量分数还不能反映不同振动能级上粒子分布.图3分别给出了基态和第30振动能级的N2（v）粒子数在总的N2粒子数中所占比例沿轴线的分布.由图3（a）可见，在流动冻结之前，p0＝1 atm条件下N2（0）所占比例最高，p0＝10 atm条件下最低，这对应于总压较低时气流温度较低，更多的粒子通过跃迁进入低振动能级；从N2（0）比例的冻结值来看，则是p0＝10 atm条件下最高，p0＝1 atm条件下最低.这是由于压力较低条件下能级分布较早地进入冻结状态.较高振动能级的粒子比例分布的变化特点及总压条件的影响则与基态能级情况相反，这可由图3（b）看出.

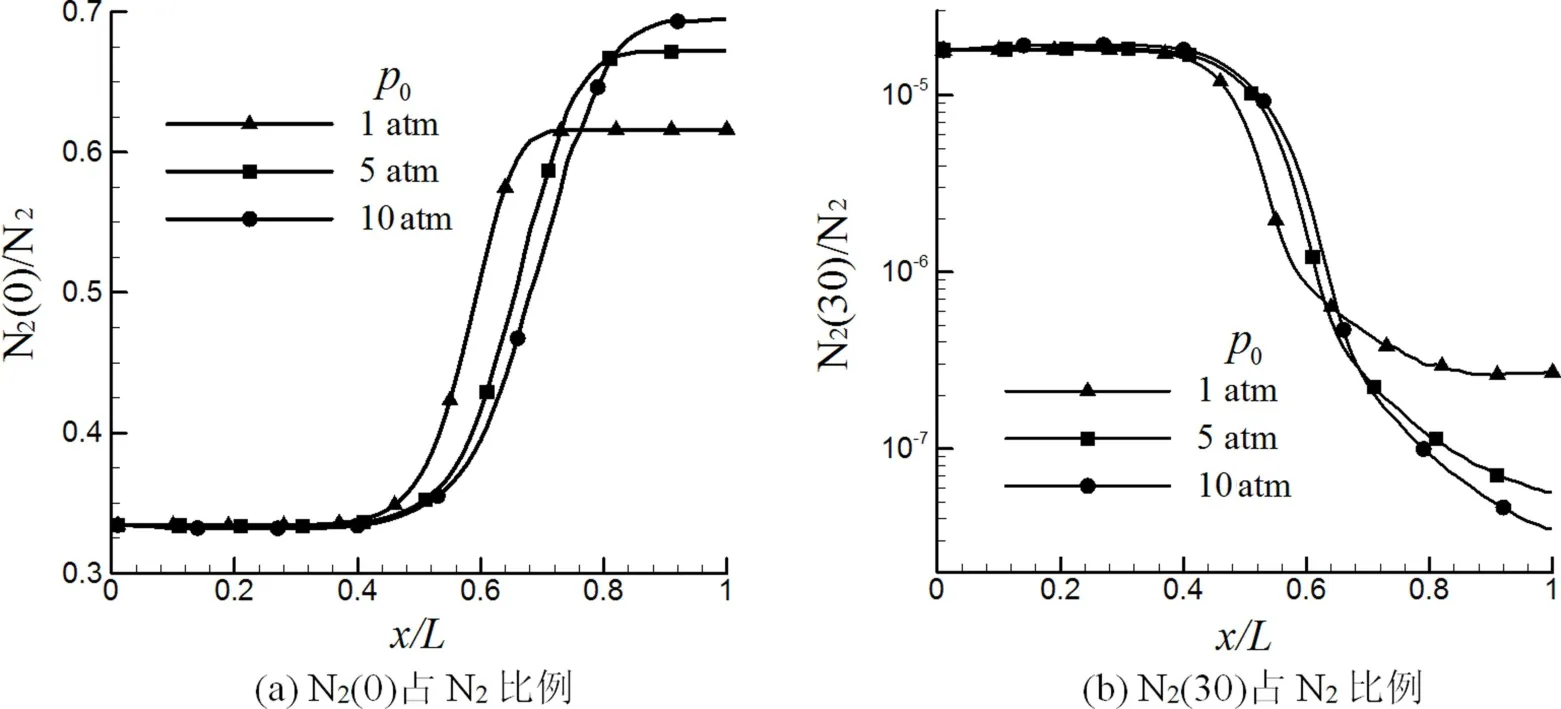
图3 T0＝8 000 K条件下N2（v）占N2比例沿喷管轴线分布Fig.3 Distribution of ratio of N2（v）in N2along the axis of nozzle at T0＝8 000 K

2.1.2 喷管不同位置的振动能级分布

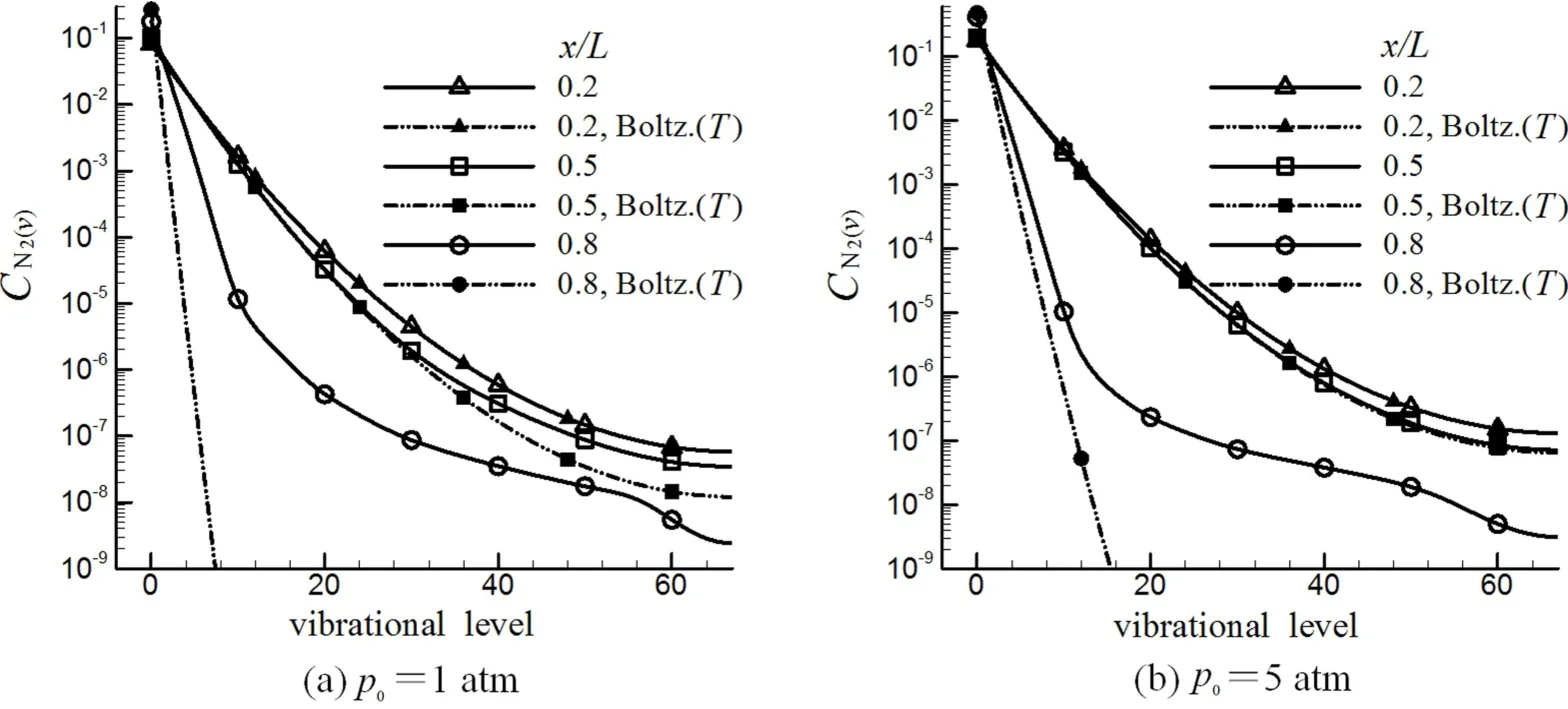
图4 T0＝8 000 K条件下CN2（v）分布与Boltzmann分布Fig.4 Distributions of CN2（v）and Boltzmann distribution at T0＝8 000 K

图4分别给出了p0＝1 atm、5 atm条件下，喷管轴线位置为x／L＝0.2、0.5、0.8处的各振动能级上的质量分数.图中实线代表态－态模型计算得到的实际振动能级分布，虚线代表该位置处流场平动温度下的Boltzmann分布.可见在x／L＝0.2处，两分布基本重合，说明此处流动仍接近振动平衡，这是由于流动速度还很低，温度压力和驻室相比也没有明显下降，流动过程中分子间可进行足够多的碰撞以使振动能级分布达到当地温度下的平衡态.在x／L＝0.5（喉道）处，p0＝1 atm条件下的两种分布出现差别，高能级上N2（v）的质量分数要高于当地温度下的Boltzmann分布值，这表明气流在膨胀降温和加速过程中，粒子并没有及时完成由高能级向低能级的跃迁，流动出现振动非平衡；而在p0＝5 atm的条件下，两种分布仍基本重合，这是由于压力增加提高了碰撞频率，推迟了喷管流动中非平衡的出现.在x／L＝0.8处，实际振动能级分布与当地温度下Boltzmann分布的差别在p0＝1 atm（图4（a））、5 atm（图4（b））和10 atm（图不再给出）条件下都非常明显，除基态外，各能级N2（v）质量分数都要高于Boltzmann分布值，并且总压越低，差别越大.这是因为喉道下游气流温度和压力（密度）的降低与速度的增加都非常迅速，粒子间碰撞频率明显降低，非平衡程度进一步加剧，流动甚至趋近于化学和热力学冻结.

图4明显地反映出喷管流动中的振动非平衡现象.双温度或多温度模型通过引入表征非平衡振动能的振动温度描述振动非平衡，隐含假设振动能级分布满足振动温度下的Boltzmann分布.这里对该假设的合理性做进一步分析.首先根据本文采用了态－态模型计算得到的细致振动能级分布和各能级能值求得总的非平衡振动能，再采用和双温度模型中类似的办法折算出振动温度，然后比较本文得到的振动能级分布和该振动温度下的Boltzmann分布.

图5给出了T0＝8 000 K，p0＝1 atm、5 atm和10 atm条件下，平动温度和振动温度沿喷管轴线的分布.可见喉道前和喉道后部分区域振动温度与平动温度都是基本重和的（高总压条件下重合区域更大），在气流继续流向下游的过程中二者分离，平动温度仍然有明显下降，而振动温度下降缓慢并趋于冻结不变.由此可知引入振动温度确实能在一定程度上方便地反映出振动非平衡现象，但是否能够反映出细致的非平衡能级分布还需继续考察.

图6对比了T0＝8 000 K，p0＝1 atm、5 atm条件下采用了态－态模型算得的实际振动能级分布和振动温度下的Boltzmann分布.可见二者有明显偏离，与图4非常类似.当然，在x／L＝0.8处，实际振动能级分布与振动温度下Boltzmann分布的差别要比与平动温度下Boltzmann分布的差别稍小.这和喉道前及喉道后近下游平动温度与振动温度重合而在远下游处振动温度冻结在高于平动温度值的特点（见图5）是一致的.该现象表明，对实际的非平衡流动，即使引入振动温度表征非平衡振动能，也不能简单地用振动温度下的Boltzmann分布描述细致的能级分布.

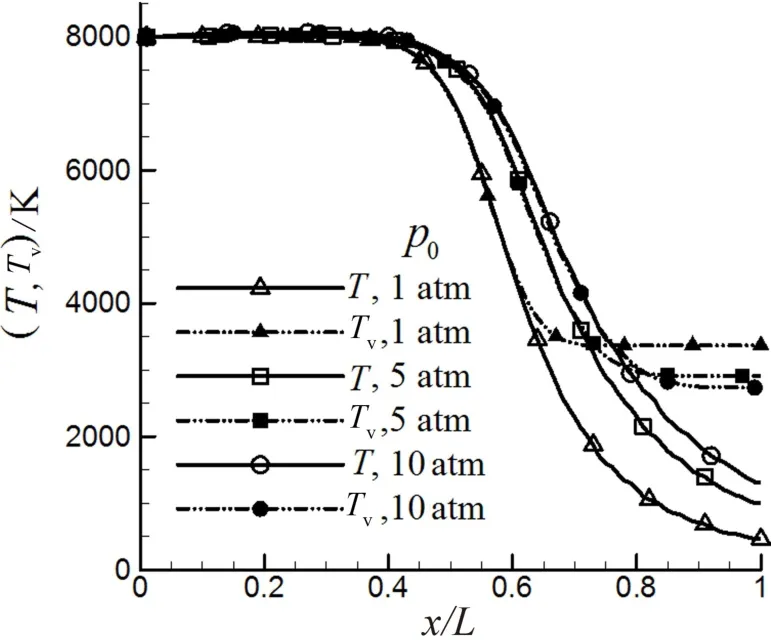
图5 T0＝8 000 K条件下平动温度和振动温度沿喷管轴线分布Fig.5 Distributions of translational and vibrational temperature along the axis of nozzle at T0＝8 000 K

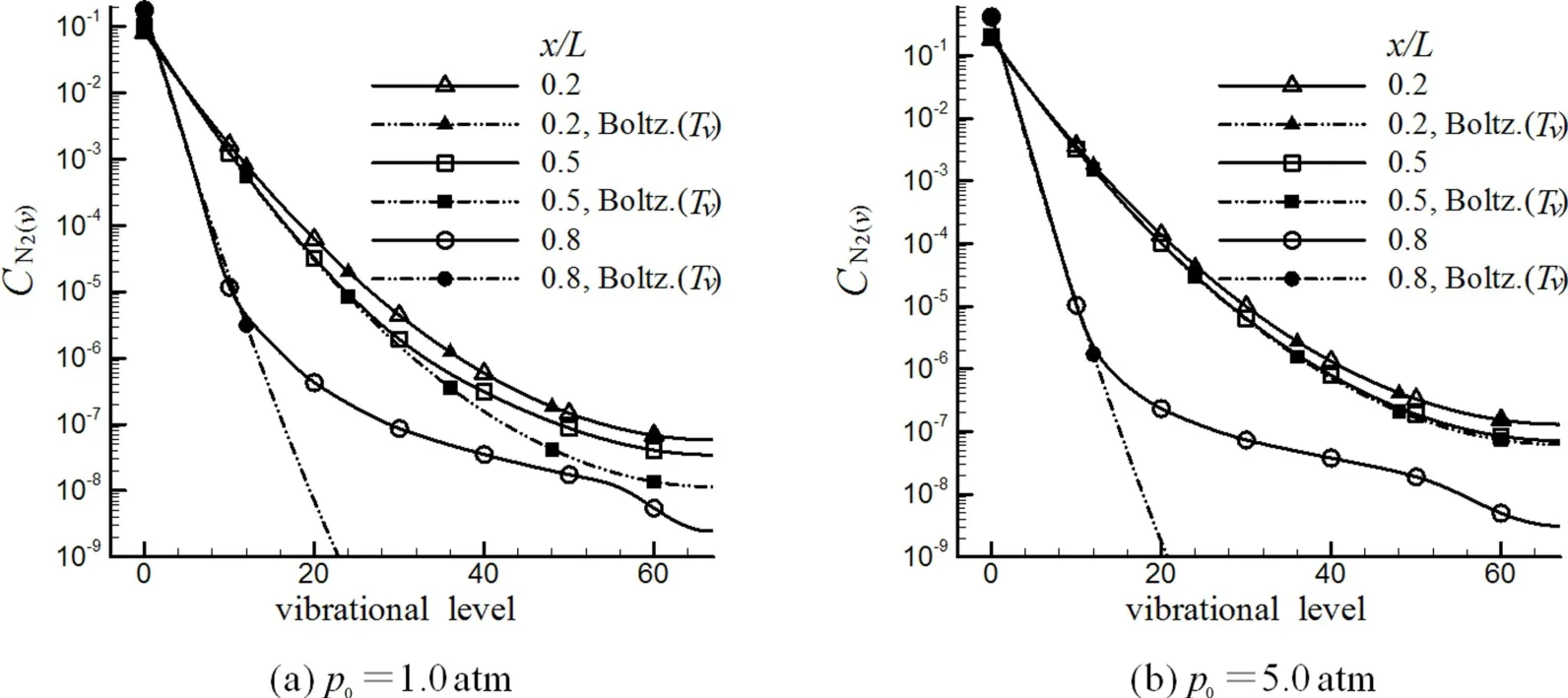
图6 T0＝8 000 K条件下CN2（v）分布与振动温度下Boltzmann分布Fig.6 Distributions of CN2（v）and Boltzmann distribution at vibrational temperature，T0＝8 000 K

2.2 T0＝3 000 K算例

该算例条件下N2的离解非常微弱.计算中发现N质量分数在喉道后出现振荡，并略有上升（见图7）.这可能是因为算例条件下N为微量组元，而68个振动能级上的N2（v）的离解或其逆反应均可能影响到它的质量分数，容易引起数值振荡.

根据这个情况，对该算例条件另外进行了只计及N2的vTm和vv过程的喷管非平衡流场计算，分析化学反应和vTa过程对宏观流动特性和微观粒子能级分布的影响.

图8对比了计及所有振动跃迁和化学反应与只计及N2的vTm和vv跃迁过程算得的温度沿喷管轴线分布，其中振动温度是根据非平衡振动能折算得出.可见化学反应和vTa过程对温度分布的影响非常有限，除入口附近无化学反应情况下算得的值略高外，其它位置是否计及化学反应得到的结果基本重合.流速、压力、密度特性也基本不受化学反应和vTa过程影响.

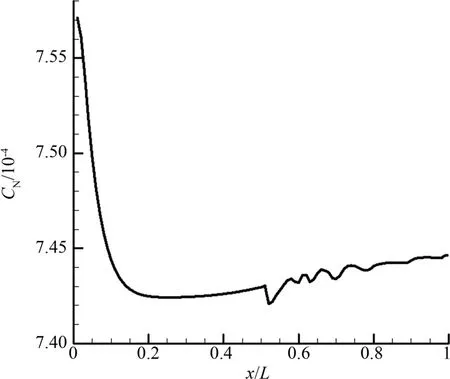
图7 T0＝3 000 K、p0＝1 atm条件下CN沿轴线分布Fig.7 Distribution of CNalong the axis of nozzle at T0＝3 000 K，p0＝1 atm

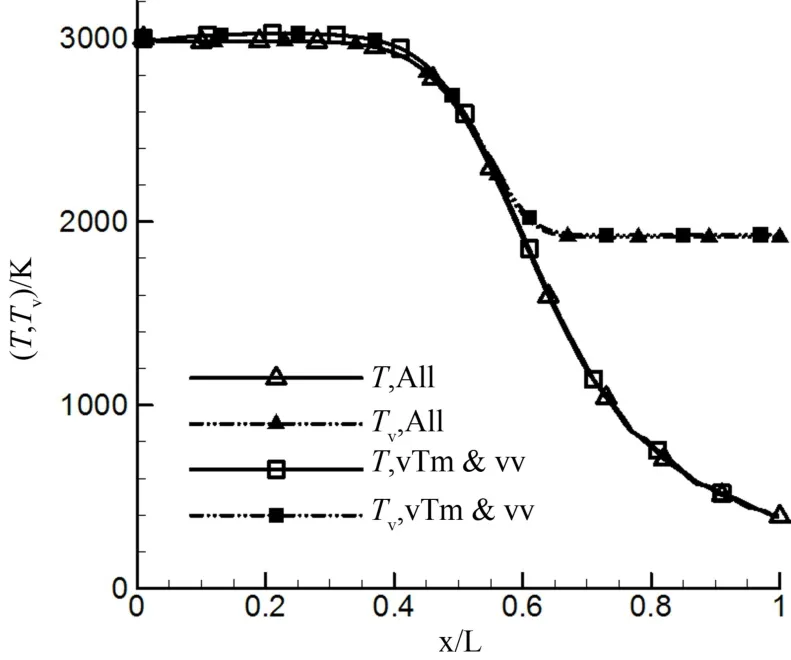
图8 T0＝3 000 K、p0＝1 atm条件下温度沿轴线分布（包含或不含化学反应）Fig.8 Distribution of temperature along the axis with or without chemical reaction at T0＝3 000 K，p0＝1 atm

但是，是否计及化学反应和vTa过程获得的粒子能级分布结果有明显差异.图9给出了喷管3个位置上的振动能级分布情况.不考虑化学反应时，振动能级分布与当地平动温度下的Boltzmann分布在喉道前及喉道附近完全重合，在下游偏离Boltzmann分布的程度也比考虑化学反应的情况下弱得多.这主要是因为N与N2高振动能级间的跃迁速率较高，而高振动能级的质量分数本身就很小，存在化学反应时N的复合会对其产生较明显的影响；而没有化学反应时，vTm和vv过程会使能级分布较快趋近于平衡态.同时可以看到此时高振动能级的质量分数很小，在10－10以下，所以虽然考虑化学反应与否得到的高振动能级分布有较明显差异，但基本不影响宏观流动特性.

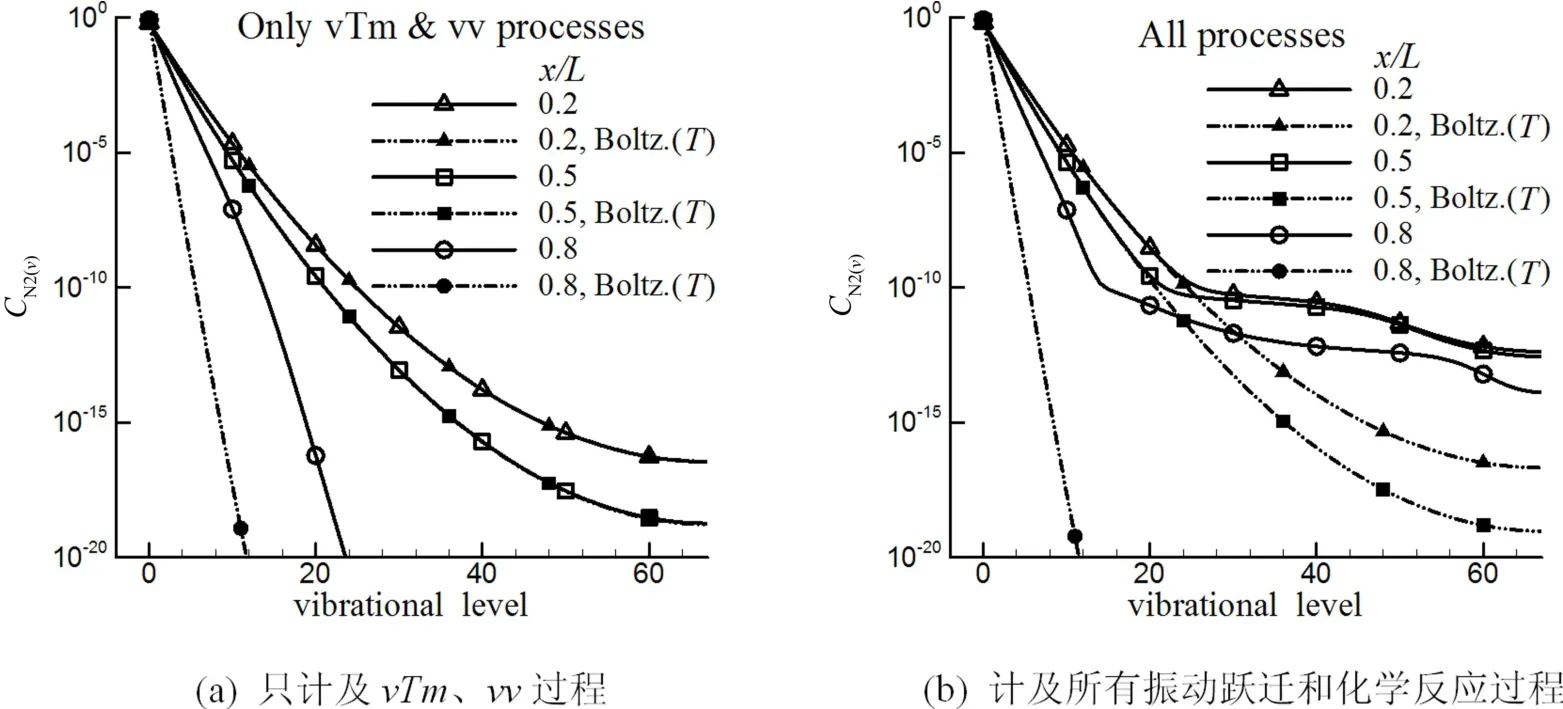
图9 T0＝3 000 K、p0＝1 atm条件下CN2（v）分布与Boltzmann分布Fig.9 Distributions of CN2（v）and Boltzmann distribution at T0＝3 000 K，p0＝1 atm

3 结论

用耦合态－态模型与流动控制方程数值研究准一维热化学非平衡喷管流，在驻室温度3 000 K～10 000 K，压力1 atm～10 atm条件下数值求解了N2／N非平衡喷管流动，分析流动宏观和微观特性，得到如下结论：

1）采用时间推进法求解耦合态－态模型的准一维非平衡喷管流，可有效解决非平衡喷管流求解时由于喉道非声速等原因造成的入口条件试凑困难问题.

2）喷管流动中喉道后振动非平衡现象显著.虽然引入振动温度能够表征非平衡振动能，却无法细致描述各振动能级上的粒子分布，真实的粒子分布与振动温度下的Boltzmann分布仍有明显差别，复合占优的膨胀流中粒子偏离平衡分布的程度比离解占优的激波后流动中更强.膨胀过程中不同振动能级分布的变化特点不同，细致的微观能级分布规律必须通过采用态－态模型获得.

3）在较低的总温条件（如T0＜3 000 K）下N2的离解非常微弱，化学反应对流场宏观特性的影响可以忽略，因此流动计算时是否考虑化学反应均可得到合理的流场宏观参数分布.但是否计及化学反应得到的高振动能级分布偏离平衡分布的程度有明显不同，本文初步分析认为不计及化学反应得到的结果更加合理，而计及微量化学反应的计算结果具有较大的数值不确定性.该问题在未来的研究中可以进一步深入.

4）态－态模型较双温度或多温度模型更具理论优势，但由于其计算量巨大，目前用于多维非平衡流动模拟还有困难.耦合态－态模型进行准一维喷管流研究，一方面更深入了解了重要非平衡区域微观过程对宏观流动特性的影响，可为改进现有的宏观热化学模型提供思路，另一方面也为未来将态－态模型用于二维或三维非平衡流动研究做了一定技术储备.

［1］Park C.Problems of rate chemistry in the flight regimes of aeroassisted orbital transfer vehicles［J］.Progress in Astronautics and Aeronautics，1985，96：511－537.

［2］Capitelli M，Armenise I，Gorse C.State-to-state approach in the kinetics of air components under re-entry conditions［J］. Journal of Thermophysics and Heat Transfer，1997，11（4）：570－578.

［3］Silva M L，Guerra V，Loureiro J.State-resolved dissociation rate for extremely nonequilibrium atmospheric entries［J］.Journal of Thermophysics and Heat Transfer，2007，21（1）：40－49.

［4］Park C.The limits of two-temperature model［R］.AIAA 2010－911，2010.

［5］Colonna G，Armenise I，Bruno D，et al.Reduction of state-to-state kinetics to macroscopic models in hypersonic flows［J］．Journal of Thermophysics and Heat Transfer，2006，20（3）：477－486.

［6］Capitelli M，Armenise I，Colonna G，Koudriavtsev N，et al.Nonequilibrium vibrational kinetics during hypersonic flow of a solid body in nitrogen and its influence on the surface heat flux［J］.Plasma Chemistry and Plasma Processing，1995，15（3）：501－527.

［7］Armenise I，Capitelli M，Gorse C.Nitrogen nonequilibrium vibrational distribution and non-Arrhenius dissociation constants in hypersonic boundary layers［J］.Journal of Thermophysics and Heat Transfer，1998，12（1）：45－51.

［8］Colonna G，Tuttafesta M，Capitelle M，et al.NO formation in one-dimensional nozzle air flow with state-to-state nonequilibrium vibrational kinetics［R］.AIAA 98－2951，1998.

［9］Colonna G，Tuttafesta M，Capitelle M，et al.Non-Arrhenius no formation rate in one-dimensional nozzle air flow［J］.Journal of Thermophysics and Heat Transfer，1999，13（3）：372－375.

［10］戴东旭，杨学明.基元化学反应态态动力学研究［J］.化学进展，2007，19（11）：1633－1645.

［11］徐丹，张威，曾明，等.态－态模型下N2／N系统的热化学非平衡过程研究［J］.空气动力学学报，2014，32（3）：280－288.

［12］Colonna G，Pietanza L D，Capitelle M.Recombination-assisted nitrogen dissociation rates under nonequilibrium conditions ［J］.Journal of Thermophysics and Heat Transfer，2008，22（3）：399－406.

［13］Esposito F，Armenise I，Capitelli M.N-N2State to state vibrational-relaxation and dissociation rates based on quasiclassicalcalculations［J］.Chemical Physics，2006，331：1－8.

［14］柳军.热化学非平衡流及其辐射现象的实验和数值计算研究［D］.长沙：国防科学技术大学，2004.

［15］徐丹.高温热化学非平衡模型研究［D］.长沙：国防科学技术大学，2012.

Numerical Study of Thermochemical Nonequilibrium Nozzle Flow in State-to-State Model

XU Dan，ZENG Ming，ZHANG Wei，LIU Jun
（College of Aerospace Science and Engineering，National University of Defense Technology，Changsha 410073，China）

A state-to-state model is used to simulate thermochemical nonequilibrium nozzle flow of N2／N mixture.Quasi-onedimensional nozzle flow at reservoir temperature from 3 000 K to 8 000 K and pressure from 1 atm to 10 atm is simulated numerically to obtain flow properties，especially detail vibrational population distribution.Evolution of macro-and micro-properties of nonequilbrium flow during expanding is analyzed.Rationality of two-temperature or multi-temperature approach is investigated for recombination dominating flows.

state-to-state model；thermochemical nonequilibrium；vibrational population distribution；hypersonic nozzle flow；numerical simulation

date：2013－10－09；Revised date：2014－02－21

V211.22

A

2013－10－09；

2014－02－21

国家自然科学基金（11102231）资助项目

徐丹（1987－），男，辽宁凤城，博士生，主要从事计算流体力学、高温气体动力学研究，E-mail：449761494＠qq.com

1001-246X（2014）05-0531-08