冲击作用下非均质炸药热点形成的离散元方法

刘 超， 石艺娜， 梁仙红

（北京应用物理与计算数学研究所，北京 100088）

冲击作用下非均质炸药热点形成的离散元方法

刘 超， 石艺娜， 梁仙红

（北京应用物理与计算数学研究所，北京 100088）

用离散元方法模拟以HMX为基的塑料粘结炸药与HMX颗粒炸药在冲击载荷作用下的细观响应过程.结果表明对于HMX颗粒炸药，炸药颗粒界面处的温度及压力远高于颗粒内部；对于HMX为基的塑料粘结炸药，粘结剂处的温度及压力亦高于颗粒内部；两种冲击响应过程的对比分析表明，粘结剂有效地降低了炸药颗粒边界处的温度及压力.

离散元方法；热点；冲击加载；炸药

0 引言

非均质炸药的热点形成机制研究是当前爆轰物理研究的热点和难点问题之一.热点形成机制研究涉及材料物理、化学以及力学等多个学科，同时涵盖宏、细、微观多个尺度.已有研究表明非均质炸药中的杂质、气泡、孔隙、粘结剂和炸药的颗粒尺度、粘性、热容、导热系数、活化能、反应热、密度以及加载速率、应力状态、环境温度等因素都会对热点的形成与演化过程产生重要影响.因此，尽管提出了多种热点形成机制［1］，但由于炸药细观结构的多样性以及热点形成与演化的复杂性，目前尚无法通过实验或唯象理论研究对炸药内部热点的形成与演化过程进行细致描述，因而细观尺度数值模拟就成为研究此类问题的重要手段.

对非均质炸药热点机制的细观数值模拟已成为当前爆轰物理研究的前沿课题.Los Alamos国家实验室的Menikoff利用二维欧拉程序先后对颗粒炸药及含缺陷炸药，在冲击载荷作用下的热点形成过程进行了模拟［2－5］；Livermore国家实验室的Reaugh采用三维ALE（任意拉氏－欧拉有限差分）程序，模拟了不同尺度下受冲击炸药的力热响应及化学反应［6－8］；Sandia国家实验室的Baer用三维欧拉程序CTH模拟了多孔炸药的冲击响应过程［9－10］；2007年Baer在冲击波科学与技术参考丛书中专门用一章，对于冲击载荷作用下非均质炸药的细观模拟研究进行了总结［11］.

近年来，多尺度算法研究发展迅猛，但多集中于宏观尺度与微观尺度计算方法耦合的搭桥类算法研究，细观尺度的计算方法相对较少.目前，研究多晶材料冲击响应的细观尺度数值模拟方法，原则上可分为两类，一类是以离散元为代表的粒子类方法，另一类是以连续介质力学为基础的传统数值模拟方法.与传统数值模拟方法相比离散元具有构建非均质模型方法易行，颗粒间取向分布特征特性表征便捷，处理冲击载荷作用下炸药颗粒间常见的大变形、摩擦、断裂等问题方便，算法实现简单等优点.

离散元法是一种无网格方法，于20世纪70年代初由美国学者Cundall首先提出［12］，最初主要应用于岩石力学、颗粒态群体及土壤力学问题分析中.20世纪90年代初，日本学者Sawamoto［13］首先将离散元方法成功地用于混凝土动态冲击破坏等非线性大变形问题的数值模拟研究.北京大学的刘凯欣教授，在这一领域做了大量的研究工作［14－15］.1999年以来，Horie等利用离散元方法研究了铜、铁等多晶金属的冲击响应［16－17］. 2000年以后，中国科学技术大学的唐志平、王文强将离散元方法应用到非均质材料炸药在冲击作用下细观变形及损伤研究中［18］.中国工程物理研究院流体物理研究所的傅华、赵峰等利用该方法研究了HMX晶体在冲击载荷作用下，由于空洞塌缩形成的热点［19］.这些工作展示了离散元方法模拟细观非均质材料冲击动力学问题的能力.由于可以方便地表征颗粒间的取向分布特征，描述颗粒间的相互作用，离散元方法在模拟细观非均质材料的冲击响应方面具有独特的优势.

本文利用离散元方法对以HMX为基的塑料粘结炸药与HMX颗粒炸药冲击作用下的热点形成与演化过程进行模拟，探讨非均质炸药在冲击载荷作用下的细观响应特征，分析冲击过程中塑料粘结剂所起的作用.计算中仅考虑未反应炸药在冲击作用下的力、热响应，未考虑固固、固液相变及化学反应等复杂因素.

1 计算模型与方法

离散元方法通过求解多体运动的牛顿力学方程组，跟踪全部个体（即单元）的运动轨迹，来揭示系统与外界的相互作用和自身响应、演化规律.与传统数值模拟方法相比离散元具有非均质材料模型构建方法易行，颗粒间取向分布特征表征便捷，处理冲击载荷作用下炸药颗粒间常见的大变形、摩擦、断裂等问题方便，算法实现简单等优点.

1.1 单元间相互作用力模型

离散元方法的核心是根据所研究的问题，选取合适的单元间相互作用力模型.一般单元间可能包括的相互作用力，见图1［20］.

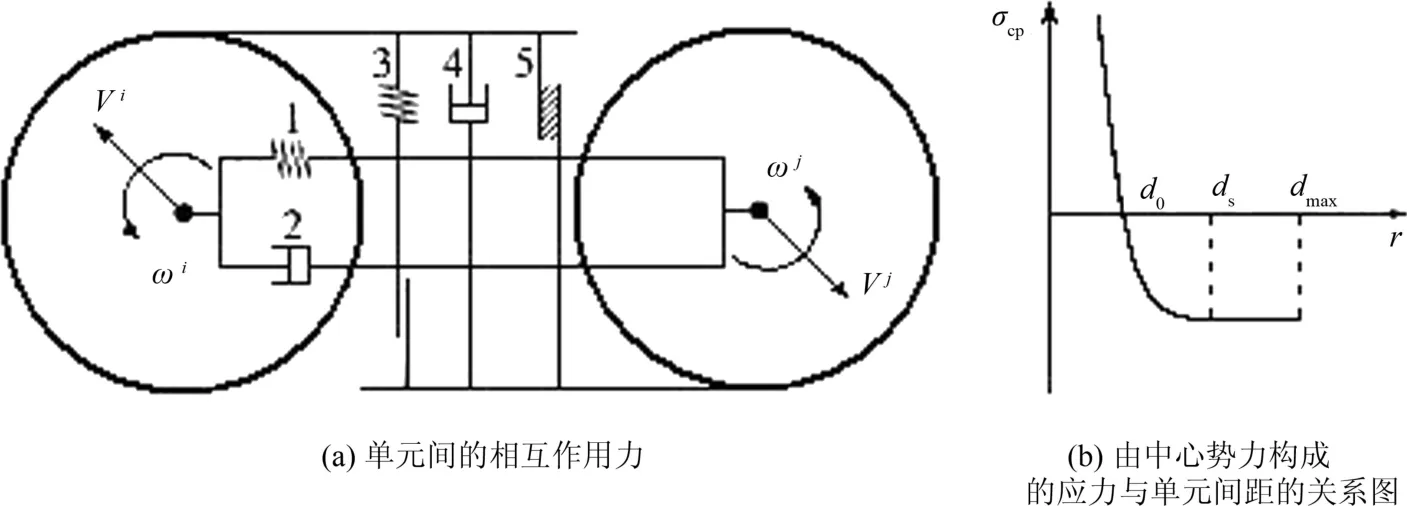
图1 DM2中单元间的相互作用力的示意图Fig.1 Schematic of interaction forces between elemonts in DM2

图1（a）中单元间的相互作用力包括：①中心势力，②中心阻尼，③弹塑性剪切力，④切向阻尼，⑤干摩擦力.图中V为线速度，ω为角速度.图1（b）为由中心势力构成的应力（σcp）与单元间距（d）的关系；当0＜d ＜ds时，材料的响应由Lennard-Johns势函数描述；当d＝ds时，材料发生屈服，屈服强度与温度有关；当d≥dmax时单元间将失去连接.如图1所示，单元i与单元j间的相互作用力合力可表示为

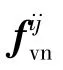
表1中，αij、m、n为中心势力参数，Cn为阻力系数，Cd为摩擦系数.

表1 单元间作用力模型参数Table1 Interaction force parameters

1.2 单元温度的计算

将影响单元温度的力学过程分为可逆过程与不可逆过程，可逆的力学过程如中心势力的作用过程，不可逆的力学过程为耗散力的作用过程

温度的可逆部分可表示为

其中，T0＝300 K为初始温度，V0为初始比体积，V为比体积，Γ为Gruneisen系数.

不可逆部分考虑了由热传导、粘性力和炸药颗粒间的摩擦力带来的能量耗散过程，不可逆过程带来的温升是上述过程的累计效应：

接触单元间考虑了基于傅立叶定律的热传导过程

ΔQ为在Δt时间内由单元j向单元i传导的热，κ为热传导系数，Ti和Tj分别为单元i与单元j的温度，dij为单元i与单元j间的距离，Aij为单元i与单元j间的接触面积.

由热传导导致的单元温度变化，表示为

由粘性力带来的温升

其中，M为单元质量，cV为等容比热，Cn为粘性系数，vijn为单元间法向速度.

炸药颗粒间的摩擦力仅存在于炸药颗粒边界处的单元内，炸药颗粒内部的单元间不考虑摩擦力.由摩擦力带来的温升表示为

表2 热力学参数Table 2 Thermodynamic parameters

其中，Cd为摩擦系数，Nij为单元间的正压力，vijt为单元间切向速度.单元温度计算中热力学参数的取值参见表2.

2 均质HMX炸药的数值模拟及结果分析

计算模型中飞片与靶板分别取300 μm×1.2 μm与900 μm×1.2 μm的均质HMX炸药，单元直径为0.4 μm，计算单元总数10 392个.如图2所示，计算模型的上、下边界采用周期性边界条件，左、右边界采用自由边界条件.模型初始温度300 K，初始时刻飞片不同的速度从左端撞击靶板.

图3给出了HMX的P-V／V0Hugonoit曲线，图中实心方块为Yoo等人的实验数据［21］，实心三角为LASL实验室的实验数据［22］，实线为本文计算结果.图4中点划线为Menikoff［3］等利用Hayes状态方程得到的结果，实线为本文采用上述温度计算模型得到的计算结果.计算结果与文献中的实验结果或数值模拟结果符合较好，证明计算所用单元间作用力模型及温度计算模型能够正确反应HMX的冲击压缩特性.

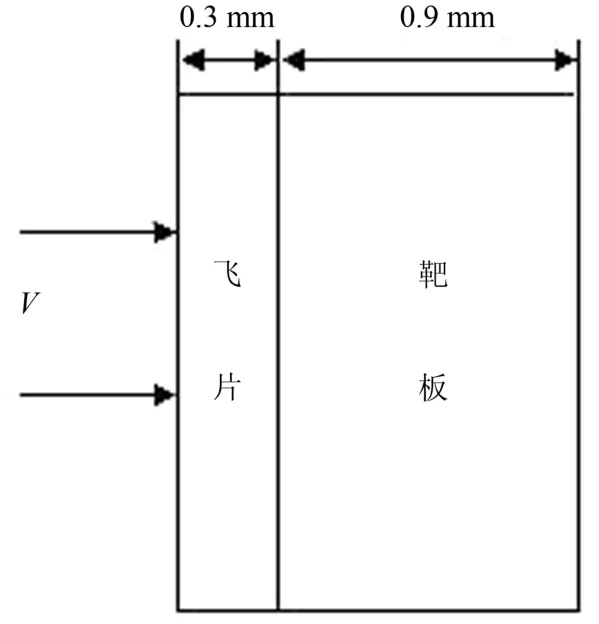
图2 计算模型示意图Fig.2 Initial model sketch

3 非均质HMX炸药的数值模拟及结果分析

从细观尺度看，固体炸药是典型的非均质材料，其细观结构特征将显著影响其动态响应过程：王金英等人在落锤实验中发现，粘结剂可以有效降低炸药感度［23］.传统的数值模拟方法难以表征炸药颗粒间的取向分布特征，及其在冲击载荷作用下可能出现的大变形、摩擦、断裂等问题，因而在模拟细观非均质材料响应方面遇到较大困难，而离散元方法在模拟此类问题时具有独特的优势.本文采用离散元方法对于以HMX为基的塑料粘结炸药与HMX颗粒炸药，在冲击作用下的热点形成与演化过程进行了数值模拟研究.

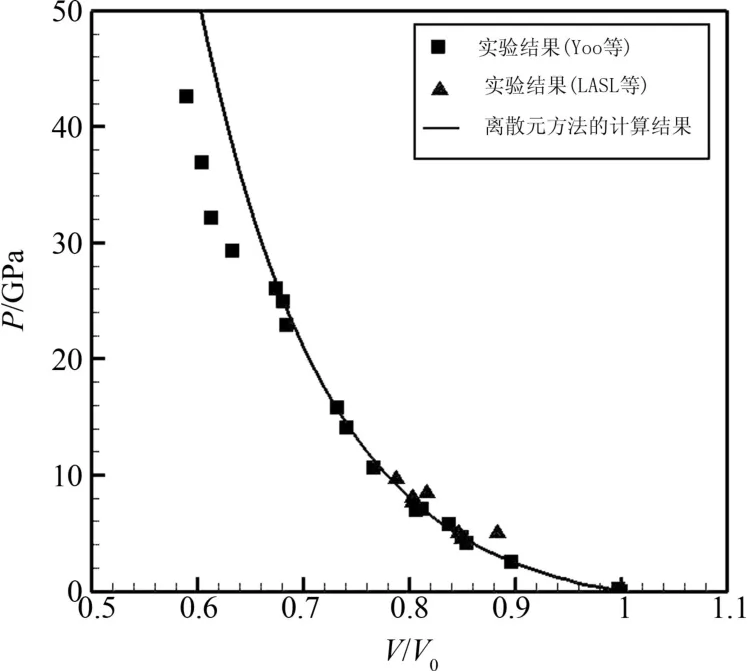
图3 HMX的P-V／V0Hugoniot关系Fig.3 P-V／V0Hugonoit of HMX

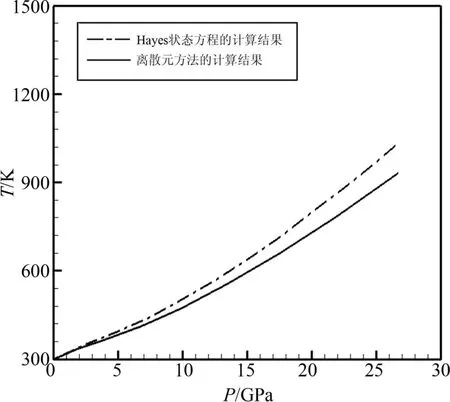
图4 HMX的P-T关系Fig.4 P-T relation of HMX

为避免边界效应的影响，计算模型的左、右边界为周期型边界条件，下边界为固壁边界，上边界为自由边界，初始时刻计算模型（见图5）以1 km·s－1的速度撞击固壁.

图5 HMX颗粒炸药与以HMX为基的PBX炸药初始计算模型Fig.5 Initial model of granule HMX and PBX

图5中不同颜色的颗粒代表颗粒间不同的晶粒取向，计算模型中的每个炸药颗粒的晶粒取向呈随机分布，以此表征炸药颗粒间的取向分布特性.图6为计算模型的放大图，可见颗粒内部单元为规则的密排六边形，颗粒处的间隙由小尺度单元填满，各颗粒的晶粒取向为（0°～60°）之间的随机数.图5与图6中PBX炸药计算模型的颗粒边界处可见黑色的单元，代表塑料粘接剂Estane.

图6 HMX颗粒炸药与以HMX为基的PBX炸药模型局部放大图Fig.6 An enlarged view of granule HMX and PBX

图7为HMX颗粒炸药与以HMX为基的PBX炸药模型分别以1 km·s－1速度撞击固壁后，某时刻流场内的压力分布图.图8着重显示了同一时刻，两种炸药内部压力高于10 GPa的区域.可以看到由于炸药颗粒间取向差异及颗粒边界效应的影响，压力场的分布很不均匀，应力远高于或低于波后平均应力的区域集中于颗粒边界附近.并且虽然构建的PBX炸药模型中粘结剂的组分含量很低，其质量百分比约4%，但其缓冲作用显著，从图8可见以HMX为基的PBX炸药受冲击后的较高压力区明显少于HMX颗粒炸药.

图7 两种炸药受冲击后的压力分布Fig.7 Pressure fields in two models

图8 两种炸药受冲击后的高压位置分布Fig.8 High pressure positions in two models

图9为两种炸药同一位置的压力放大图，图9（a）为HMX颗粒炸药的颗粒取向与压力放大图，图9（b）为PBX炸药的物质与压力放大图.可见应力远高于或低于波后平均应力的区域集中于粘结剂或炸药颗粒边界附近，并且PBX炸药粘结剂处的压力明显低于HMX炸药颗粒边界处的压力.这是由于粘结剂较软，起到一定的缓冲作用，有效地降低了PBX炸药颗粒边界处的压力.

图10为HMX颗粒炸药与以HMX为基的PBX炸药模型分别以1 km·s－1速度撞击固壁后，某时刻波后流场内的温度分布图.图11着重显示了同一时刻，两种炸药内部温度高于700 K的区域.可以看到波后的温度场的分布很不均匀，由于炸药颗粒间的取向差异及颗粒边界的影响，温度远高于或低于波后平均温度的区域主要集中于炸药颗粒边界或粘结剂区域附近.尽管PBX模型中粘结剂所占百分比很少，但由于粘结剂较软易于变形，并在变形过程中吸收冲击能量，使得PBX炸药的热点温度明显低于颗粒炸药，如图11.

图9 两种炸药受冲击后的压力放大图Fig.9 Amplified pressure fields in two models

图10 两种炸药受冲击后的温度分布Fig.10 Temperature fields in two models

图11 两种炸药受冲击后高温位置分布Fig.11 High temperature positions in two models

4 结论

用离散元方法模拟了HMX炸药的冲击响应过程，得到了HMX的冲击Hugoniot关系与P-T关系，计算结果与文献中的实验结果及数值模拟结果符合较好，证明计算所用单元间作用力模型及温度计算模型能够正确反应HMX的冲击压缩特性.对于以HMX为基的塑料粘结炸药与HMX颗粒炸药在冲击载荷作用下的细观响应过程进行了数值模拟，结果表明对于HMX颗粒炸药，炸药颗粒界面处的温度及压力明显高于颗粒内部；对于HMX为基的PBX炸药，粘结剂处的温度及压力亦高于颗粒内部；对于上述两种冲击响应过程的比较表明粘结剂较软，能起到一定的缓冲作用，并在变形过程中吸收冲击能量，从而有效的降低了炸药颗粒边界处的温度与压力.

［1］Field J E.Hot spot ignition mechanisms for explosives［J］.Acc Chenm Res，1992，25：489－496.

［2］Menikoff R.Pore collapse and hot spots in HMX［C］∥Conferences on Shock Compression of Condensed Matter，2004，706：393－396.

［3］Menikoff R，Sewell T D.Constituent properties of HMX needed for mesoscale simulations［J］.Combust Theory Model，2002，6：103－125.

［4］Menikoff R.Granular explosives and initiation sensitivity［C］∥Conferences on Shock Compression of Condensed Matter，2002，979－983.

［5］Menikoff R.Hot spot formation from shock reflections［J］.Shock Wave，2011，21：141－148.

［6］Reaugh J E.Grain-scale dynamics in explosive［R］.Lawrence Livermore National Laboratory，UCRL-ID－150388.2002.

［7］Reaugh J E.First results of reaction propagation rates in HMX at high pressure［C］∥Conferences on Shock Compression of Condensed Matter，2003：401－404.

［8］Reaugh J E.Multi-scale computer simulations to study the reaction zone of solid explosives［C］∥Proceedings of the 13th Int Symp on Detonation，2006：1276－1285.

［9］Baer M R，Trott W M.Mesoscale descriptions of shock-loaded heterogeneous porous materials［C］∥Conferences on Shock Compression of Condensed Matter，2001：713－716.

［10］Baer M R.Modeling heterogeneous energetie materials at the mesoseale［J］.Thermochimic Acta，2002，384：351－367.

［11］Baer M R，Trott W M.Mesoscale studies of shock loaded tin spheres［C］∥Conferences on Shock Compression of Condensed Matter，2003：517－520.

［12］Cundall P A.A computer model for simulating progressive large scale movement in blockrock system［J］.Symposium ISRM，1971，（2）：129－136.

［13］Sawamoto Y，Tsubota H，Kasai Y，Koshika N，Morikawa H.Analytical studies on local damage to reinforced concrete structures under impact loading by discrete element method［J］.Nucl Eng Des，1998，179：157－177.

［14］刘凯欣，高凌天，郑文刚.混凝土动态破坏过程的数值模拟［J］.工程力学（增刊），2000：470－474.

［15］刘凯欣，高凌天.离散元法在求解三维冲击动力学问题中的应用［J］.固体力学学，2004，25（2）：181－185.

［16］Yano K，Horie Y.Discrete-element modeling of shock compression of polycrystalline copper［J］.Phys Rev B，1999，59：13672－13680.

［17］Case S，Horie Y.Mesomechanics of the α-d transition in Iron［J］.J Mech Phys Solids，2007，55：589－614.

［18］王文强.离散元方法及其在材料和结构力学响应分析中的应用［D］.合肥：中国科学技术大学，2000.

［19］傅华，赵峰，谭多望，王文强，尚海林.冲击作用下HMX晶体孔洞塌缩热点生成机制的细观数值模拟［J］.高压物理学报，2011，25（1）：8－14.

［20］Tang Z P，Horie Y，Psakhie.Diserete meso-element modeling of shock processes in powders［M］∥Graham R A，et al.Shock Compression of Solids，IV.Springer-Verlag，1997：143－176.

［21］Yoo C S，Cynn H.Equation of state，phase transition，decomposition of β-HMX［J］.J Chem Phys，1999，111：10229－10235.

［22］Marsh S.LASL shock Hugoniot data［M／OL］.Univ Calif Press，1980，http：／／lib-www.lanl.gov／books／shd.pdf.

［23］王金英，柴涛，张景林.PBX传爆药撞击感度影响因素的研究［J］.华北工学院学报，2004，25（4）：289－292.

DEM Study on Hot Spots Formation of Heterogeneous Explosives Under Shock Loading

LIU Chao，SHI Yina，LIANG Xianhong
（Institute of Applied Physics and Computational Mathematics，Beijing 100088，China）

Mesoscale responses of plastic boned explosives（PBX）and grannular HMX under shock loading were investigated with discrete element method（DEM）.It shows that for shocked grannular HMX temperature and pressure in grain boundary are much higher than those of inner HMX crystals.In the case of shocked PBX high temperature and pressure regions are mostly located in binder and near parts.Comparisons show that temperature and pressure in grain boundary are effectively reduced by binder.

discrete element method；hot spot；shock loading；explosive

date：2013－10－28；Revised date：2014－03－20

O347.1

A

2013－10－28；

2014－03－20

国家自然科学基金（11202034）；中物院科学技术发展基金（2011B0101028，2013B0101013）及中物院科学技术重点基金（2012A0101004）资助项目

刘超（1976－），女，硕士，副研究员，主要从事计算爆炸力学研究，E-mail：liu_chao＠iapcm.ac.cn

1001-246X（2014）05-0523-07