三角形钠原子团簇中的表面等离激元

尹海峰， 曾春花

（1.凯里学院物理与电子工程学院，贵州凯里 556011；2.凯里学院数学科学学院，贵州凯里 556011）

三角形钠原子团簇中的表面等离激元

尹海峰1， 曾春花2

（1.凯里学院物理与电子工程学院，贵州凯里 556011；2.凯里学院数学科学学院，贵州凯里 556011）

运用含时密度泛函理论研究等边三角形钠原子团簇中的表面等离激元激发.发现：在团簇尺寸较大时，沿三角形底边和底边中垂线方向激发的共振模式不同，然而沿两方向的吸收光谱线形一样，主要吸收峰的共振能量也相同.低能聚集共振在空间引起电场增强的极大值主要分布在三角形的端点附近.

等离激元；含时密度泛函理论；团簇

0 引言

表面等离激元（surface plasmon）是金属表面自由电子同入射光子相互耦合形成的非辐射电磁模式，是局域在金属和介质表面传播的一种混合激发态［1］.金属表面自由电子在入射光场的激励下集体相干振荡，这种共振相互作用产生了表面等离激元.近年来，随着纳米科学与技术的进步，低维人造结构不断出现，纳米结构中表面等离激元的研究越来越受到关注.通过胶体刻蚀（collodial lithography）［2］、电子束刻蚀（electron beam lithography）［3］和化学方法［4］等多种手段可以制备出纳米环、纳米壳层等［5］.这些纳米结构有独特的光学性质.它们在单分子光谱、生物医学治疗、催化反应、等离子体纳米器件等方面有重要的应用前景［6－9］.纳米结构中的表面等离激元的能量，一方面依赖于它们所处的介电环境；另一方面，依赖于纳米结构的尺寸大小和形状［10］.

团簇是一类特殊的纳米结构.随着原子数的减少，团簇的大小可以从纳米尺度过渡到原子尺度，其表面等离激元的能量也会随着团簇尺寸的变化而变化.实验和理论上对于碱金属钠原子不同团簇中表面等离激元的激发已做了许多工作.Ekardt等人用凝胶模型很好地描述了钠原子团簇中表面等离激元的激发能量［11］.Broglia及其同事采用无规相近似和含时密度泛函理论研究了小于20个原子的球形碱金属钠团簇中的等离激元共振［12－13］.发现随着球半径的改变，主要的光谱吸收峰发生劈裂，即等离激元劈裂；并认为电子—空穴对的相互作用是造成等离激元劈裂的主要原因.最近，Li等人采用含时密度泛函理论研究了尺度较大的球形钠团簇的等离激元［14］.他们发现随着球形钠团簇尺度的增大，体系的吸收光谱中有一个主要的吸收峰.实验上，Selby等人研究了钠原子团簇（Nan，4≤n≤40）的光吸收谱，同样发现电子的聚集激发对于团簇的尺寸具有一定的依赖性［15］.近来，人们采用含时密度泛函理论研究了线性、环形和平面形钠原子团簇的等离激元激发［16－20］.研究表明，在小金属团簇中主要存在三种等离激元共振模式：低能共振模式、高能共振模式以及非偶极聚集共振模式.其中，低能共振模式是一种长程电荷转移激发；高能共振模式来自于几乎简并的单电子激发的相互耦合.这些研究主要关注的是线形和球形钠原子团簇中的表面等离激元.我们知道由于表面等离激元的共振模式依赖于纳米结构的形状，因而对于具有其他结构钠团簇的研究，能够更加全面的认识该碱金属团簇中表面等离激元的共振机制.

本文研究等边三角形钠原子团簇中表面等离激元的激发.分析电子的聚集激发，随着三角形尺寸大小的演化规律；不同激发模式对应的诱导电荷分布；以及表面等离激元激发时，在空间形成的电场分布.

1 计算方法

我们采用含时密度泛函理论［21］来计算团簇的吸收光谱.含时密度泛函理论是密度泛函理论的延伸，同样从电子密度的角度来研究体系的物理性质.类似于密度泛函理论中的Kohn-Sham方程，考虑一个没有相互作用的多电子体系，其电子密度分布和具有相互作用的多电子体系的电子密度分布相同.由Runge-Gross定理，含时的Kohn-Sham势VKS（r，t）和含时的电子密度ρ（r，t）是一一对应的.没有相互作用的多电子体系满足含时的Kohn-Sham方程

外势场Vext（r，t）包括外加的电场势和原子实势.体系的含时电子密度为

含时的交换关联势Vxc（r，t）需要对含时交换关联能对含时波函数变分而得到.含时密度泛函理论现在已经成为计算多电子体系中电子激发态最常用的方法之一.这里我们采用的是利用时间演化方法来计算电子的激发态.在团簇的基态计算得到电子的占据态信息后，通过时间演化波函数的方法来计算电子的激发态.在时间t＝0时刻使所有波函数有个瞬时的相位移动［22］

其中k0为沿z方向所加的微扰外场动量．这相当于加E（t）＝k0δ（t）的微扰外场.然后，Kohn-Sham波函数进行时间演化，可以得到含时偶极距d（t）．通过对偶极距求傅立叶变换得到动态极化率α（ω）．吸收光谱可以用偶极子强度函数（dipole-strength function）S（ω）来表示，它与极化率的关系为S（ω）＝（2ω／π）Im α（ω）．

所有的含时密度泛函计算都是用实时、实空间的OCTOPUS软件来完成［21］.钠原子用模守恒赝势来描述.对基态和激发态的计算，交换关联势使用的都是局域密度近似（Localdensity approximation）.实空间模拟所用的盒子为在每个原子上面构建一个球，球的半径为8 Å，并且在盒子内使用间距为0.3 Å的均匀格点.电子波函数随时间演化了6 000时间步，每个时间步长为Δt＝0.005ħ·eV－1.这种参数设置已成功预测了一维钠原子链中等离激元的激发特性［19－20］.

采用如图1（a）所示的笛卡尔直角坐标系，长度单位为Å.等边三角形钠原子团簇固定在xy平面内．三角形的底边位于x轴，其中底边的一个端点与原点重合.原子间距是3.72 Å，为自由双钠原子间距，颜俊等人在研究钠原子环和一维钠原子链中表面等离激元时，采用了相同的原子间距值［20］.此外，先进的原子操纵实验技术可以在固体表面得到任意形状的钠原子排列，因此我们的数值实验原则上是可以实现的.

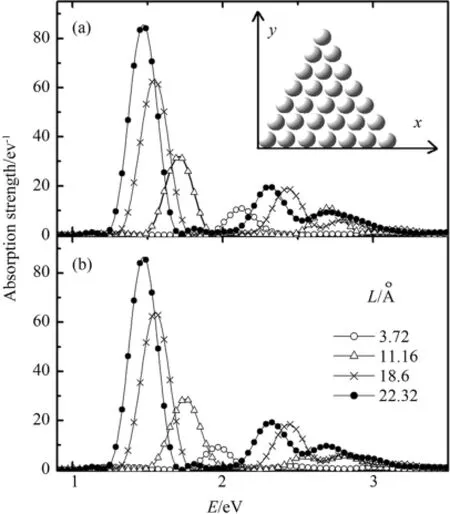
图1 三角形钠原子团簇的吸收谱（激发极化方向（a）沿Fig.1 Optical absorption of triangle sodium clusters to an impulse excitation polarized in the direction along（a）x-axis and（b）y-axis

2 结果及分析

图1（a）给出了沿x轴方向，三角形钠原子团簇随着边长L变化的偶极吸收谱的演变过程.三角形钠原子团簇的结构如图1（a）中的插图所示.图1（a）表明，沿三角形底边方向激发有一个主要的吸收峰.随着三角形边长的增加，这个主要的吸收峰不断红移，从L＝3.72 Å时的2.12 eV逐渐减小到L＝22.32 Å时的1.47 eV.这是由于随着三角形边长的增加，单电子轨道不断叠加，从而使所形成的三角形钠原子团簇的能级间距不断减小.在共振能量红移时，这个主要吸收峰的强度也在不断增加，这表明了电子激发的集体性随着电子数的增加在积累.除了主要的吸收峰外，在团簇的尺寸较大时，在高能共振区还出现了一些小的吸收峰.随着三角形钠原子团簇边长的进一步增大，这些小的吸收峰也发生红移，并且强度有所增加.在L＝22.32 Å的三角形团簇中，这两个小的吸收峰分别位于2.31 eV和2.71 eV.它们是高阶的激发模式.随着碱金属钠纳米结构的增加，主要的吸收峰以及小的吸收峰的演变规律，同Shuford等人用离散偶极近似（DDA，discrete dipole approximation）研究贵金属三角形纳米结构中表面等离激元的演化规律相同［23］.他们发现，随着金三角形边长的增加，偶极共振能量点发生红移.随后，Nelayah等人在实验上对贵金属三角形金纳米结构中表面等离激元的研究证实了这一结论［24］.Shuford等人的研究也发现了高阶的激发模式.此外，对于球形和线性钠团簇的研究表明，随着团簇尺度的增大，体系中出现高阶的等离激元模式［13，19］.

图2 三角形钠原子团簇共振频率的诱导电荷分布，（a）和（b）沿x轴方向极化，能量共振点为1.47 eV和2.31 eV，（c）和（d）沿y轴方向极化，能量共振点为1.47 eV和2.32 eVFig.2 Fourier transform of induced charge-density responses at energy resonances（a）1.47 eV and（b）2.31 eV to an impulse excitation polarized in x-axis direction；at energy resonances（c）1.47 eV and（d）2.32 eV to an impulse excitation polarized in y-axis direction

图1（b）给出沿y轴方向，三角形钠原子团簇随着边长L变化时，偶极吸收谱的演变．在团簇尺寸较小时，同沿x轴方向吸收光谱一样，有一个主要的吸收峰，但是他们的共振能量点不同．在L＝3.72Å，沿x轴方向激发时，主要吸收峰的能量共振点位于2.12 eV；而沿y轴方向激发时，主要吸收峰的能量共振点位于1.97 eV.此外，在团簇尺寸较小，光谱的线形也不相同.在L＝11.16 Å，沿x轴方向激发时，有两个吸收峰；而沿y轴方向激发时，有三个吸收峰.然而，通过对比图1（b）和1（a），我们发现随着三角形边长的增加，当团簇尺寸较大时，尽管极化方向不同，沿两个方向的吸收光谱的演化规律几乎相同.最有意义的是，在三角形团簇尺寸较大时，不但沿x轴和y轴方向吸收光谱的线形完全一样，而且各个吸收峰的共振能量点也几乎相同，尤其是主要吸收峰的能量完全相同.对于尺度较大的球形钠团簇，Li等人的研究表明体系的吸收光谱中也有一个主要的吸收峰；沿不同方向激发时，体系的吸收光谱相同［14］.对于三角形钠团簇，尽管其对称性没有球形钠团簇的高，然而在尺度较大时，沿三角形钠团簇所在的平面不同方向激发时，体系的吸收光谱也相同.此外，Talebi等人在实验和理论上，对贵金属三角形金纳米结构中表面等离激元的研究中，也发现尽管沿三角形的底边和底边中垂线方向的共振模式不同，但它们的共振能量是相同的［25］.

图2是三角形钠原子团簇共振频率的傅立叶变换诱导电荷分布.傅立叶变换的诱导电荷为

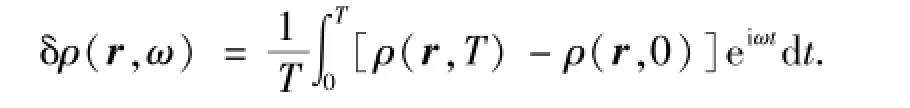
通过变换，可以得到该频率集体激发所对应电荷的空间分布.图2（a）和2（c）分别是沿x轴和y轴方向激发时，主要聚集共振所对应的诱导电荷分布（三角形边长L＝22.32 Å，具有相同共振能量为1.47 eV）.结果表明，它们有着共同的激发特征.首先，这些共振模式对应的空间诱导电荷都分布在三角形团簇的端点区域；其次，这些电荷分布都具有偶极子的特征.图2（b）和（d）分别是沿x轴和y轴方向激发时，聚集共振分别对应的诱导电荷分布（三角形边长L＝22.32Å，共振能量分别为2.31 eV和2.32 eV）.这些诱导电荷分布呈现多极距振动，表明这些聚集共振为高阶振动模式.此外，诱导电荷密度在原子附近会呈现振荡行为，如图2所示.这来自于原子势的局域调制.三角形团簇本身的空间受限与局域原子束缚互相竞争，决定了三角形团簇中集体激发的空间分布.其中，局域原子束缚是指电子受到原子势的局域约束，其强度可以通过价电子的结合能来反映.

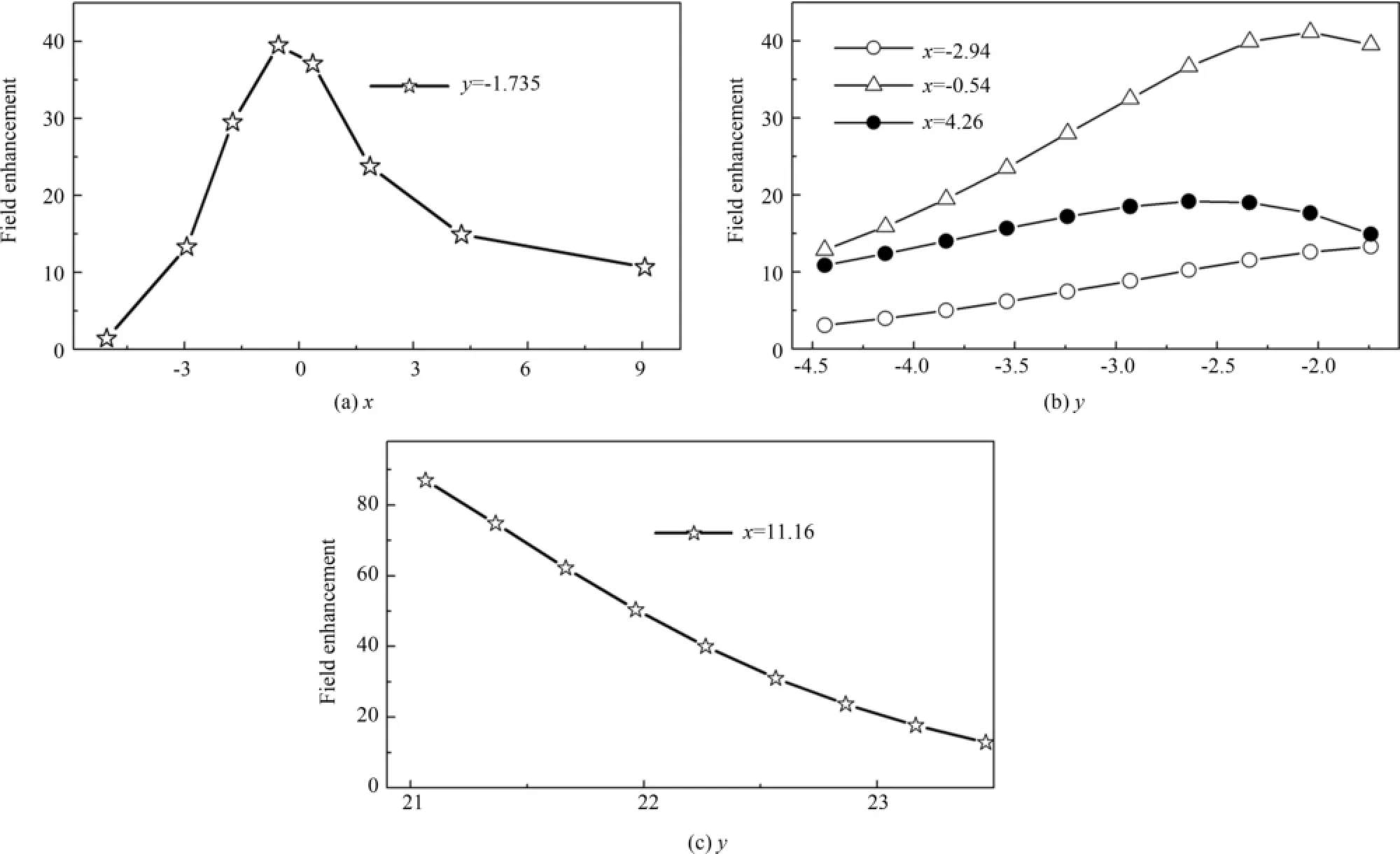
图3 沿y轴极化时，能量共振点1.47 eV对应的沿空间各直线电场的增强，（a）沿直线y＝－1.735，（b）沿直线x＝－2.94，x＝－0.54和x＝4.26，（c）沿直线x＝11.16Fig.3 Calculated field enhancement at energy resonance 1.47 eV，to an impulse excitation polarized in y-axis direction，（a）along straight line y＝－1.735；（b）along straight lines x＝－2.94，x＝－0.54 and x＝4.26；（c）along straight line x＝11.16

为了探讨表面等离激元对团簇表面场强的影响，我们计算了沿y轴激发时，主要聚集共振（能量为1.47 eV）在空间引起电场的增强，即图2（c）所示共振模式在空间引起电场的增强.空间电场增强（fieldenhancement，FE）定义为

其中e为一个电子所带的电荷，Veff为有效势，δy为一个格点边长，所建立的直角坐标系如图1（a）插图所示.图3（a）是电场沿直线y＝－1.735的增强，即沿x轴方向，靠近三角形团簇底边的电场增强．随着x值的增大，FE逐渐增强，在原点（即三角形团簇的底边端点）附近达最大值；之后又随着x值的增大在底边中部有一个极小值．由对称性可知FE在另一个底边端点处再次达到极大值.Talebi等人在实验和理论上，对贵金属三角形金纳米结构中表面等离激元的研究中，同样发现低能聚集共振引起的FE最大值分布在三角形团簇的端点附近［25］.图3（b）是电场沿y轴方向，靠近三角形团簇底边沿直线x＝－2.94，x＝－0.54和x＝4.26的增强．结果表明，在向三角形底边端点靠近时，FE是增大后又逐渐减少．这主要是由于，钠原子位于原点，当靠近原点时，由于屏蔽效应，会使FE降低.图3（c）是电场沿y轴方向，靠近三角形团簇顶点沿直线x＝11.16（即三角形底边的中垂线）的增强．结果再次表明FE最大值分布在三角形团簇的端点附近．所不同的是，在三角形顶点附近FE的最大值大约是在三角形底边端点附近FE的最大值的两倍．这主要是由于沿y轴激发时，1.47 eV处的激发为偶极共振模式，其对应的诱导电荷分布如图2（c）所示.顶点处诱导电荷密度的值大约是三角形底边端点附近诱导电荷密度值的两倍.这些结果表明，三角形碱金属钠团簇的等离激元共振在团簇表面引起的局域电场分布不均匀，在曲率半径小的位置局域电场很强，如在三角形各个顶点处.

3 结论

运用含时密度泛函理论，研究了等边三角形钠原子团簇中表面等离激元随着团簇尺寸大小变化的演化.当团簇尺寸较小时，沿底边和底边的中垂线方向激发时，各有一个吸收峰，但共振能量不同.随着团簇尺寸的逐渐增大，沿底边和底边的中垂线方向激发的吸收光谱线形一样，主要吸收峰的能量也相同，尽管它们的共振模式不同.为了探讨表面等离激元对团簇表面场强的影响，计算了沿底边中垂线方向激发时，主要聚集共振（能量为1.47 eV）在空间引起电场的增强.结果表明，低能聚集共振引起的电场增强的最大值分布在三角形团簇的端点附近.

［1］ 明海，王小蕾，王沛，等.表面等离激元的调控研究与应用［J］.科学通报，2010，55（21）：2068－2077.

［2］ Fredriksson H，Alaverdyan Y，Dmitriev A，et al.Hole-mask colloidal lithography［J］.Adv Mater，2007，19（23）：4297－4302.

［3］ Haynes C L，McFarland A D，Zhao L，et al.Nanoparticle optics：The importance of radiative dipole coupling in twodimensional nanoparticle arrays［J］.J Phys Chem B，2003，107（30）：7337－7342.

［4］ Sun Y，Xia Y.Shape-controlled synthesis of gold and silver nanoparticles［J］.Science，2010，298（5601）：2176－2179.

［5］ Aizpurua J，Hanarp P，Sutherland D S，et al.Optical properties of gold nanorings［J］.Phys Rev Lett，2003，90：057401.

［6］ Nie S，Emory S R.Probing single molecules and single nanoparticles by surface-enhanced Raman scattering［J］.Science，1997，275（5303）：1102－1106.

［7］ Bell A T.The impact of nanoscience on heterogeneous catalysis［J］.Science，2003，299（5613）：1688－1691.

［8］ Hirsch L R，Stafford R J，Bankson J A，et al.Nanoshell-mediated near-infrared thermal therapy of tumors under magnetic resonance guidance［J］.Proc Natl Acad Sci USA，2003，100（23）：13549－13554.

［9］ Maier S A，Atwater H A.Plasmonics：Localization and guiding of electromagnetic energy in metal／dielectric structures［J］.J Appl Phys，2005，98（1）：011101.

［10］ Kelly K L，Coronado E，Zhao L，et al.The optical properties of metal nanoparticles：The influence of size，shape，and dielectric environment［J］.J Phys Chem B，2003，107（3）：668－677.

［11］ Ekardt W.Size-dependent photoabsorption and photoemission of small metal particles［J］.Phys Rev B，1985，31：6360.

［12］ Yannouleas C，Vigezzi E，Broglia R A.Evolution of the optical properties of alkali-metal microclusters towards the bulk：The matrix random-phase-approximation description［J］.Phys Rev B，1993，47：9849.

［13］ Yannouleas C，Broglia R A，Brack M，et al.Fragmentation of the photoabsorption strength in neutral and charged metal microclusters［J］.Phys Rev Lett，1989，63：255.

［14］ Li J H，Hayashi M，Guo G Y.Plasmonic excitations in quantum-sized sodium nanoparticles studied by time-dependent density functional calculations［J］.Phys Rev B，2013，88：155437.

［15］ Selby K，Kresin V，Masui J，et al.Photoabsorption spectra of sodium clusters［J］.Phys Rev B，1991，43：4565.

［16］ Yin H F，Zhang H，Quantum mechanical study of plasmonic coupling in sodium nanoring dimers［J］.Appl Phys Lett，2012，101（6）：061906.

［17］ Yin H F，Zhang H，Quantum mechanical study on plasmon resonances in small ring clusters［J］.International Journal of Quantum Chemistry，2012，112（16）：2816－2821.

［18］ Yin H F，Zhang H，Collectivity of plasmon excitations in small sodium clusters with planar structure［J］.Physica B，2012，407（3）：416－420.

［19］ Yan J，Yuan Z，Gao S.End and central plasmon resonances in linear atomic chains［J］.Phys Rev Lett，2007，98：216602.

［20］ Yan J，Gao S.Plasmon resonances in linear atomic chains：Free-electron behavior and anisotropic screening of d electrons［J］.Phys Rev B，2008，78：235413.

［21］ Marques M A L，Castro A，Bertsch G F，et al.Octopus：A first-principles tool for excited electron-ion dynamics［J］.Comput Phys Commun，2003，151（1）：60－78.

［22］ Yabana K，Bertsch G F.Time-dependent local-density approximation in real time［J］.Phys Rev B，1996，54：4484.

［23］ Shuford K L，Ratner M A，Schatz G C.Multipolar excitation in triangular nanoprisms［J］.J Chem Phys，2005，123（11）：114713.

［24］ Nelayah J，Kociak M，Stéphan O，et al.Two-dimensional quasistatic stationary short range surface plasmons in flat nanoprisms［J］.Nano Lett，2010，10（3）：902－907.

［25］ Nahid T，Wilfried S，Ralf V，et al.Breaking the mode degeneracy of surface plasmon resonances in a triangular system［J］. Langmuir，2012，28（24）：8867－8873.

Plasmon Resonances in Sodium Clusters with Triangle Structure

YIN Haifeng1，ZENG Chunhua2
（1．College of Physics and Electronic Engineering，Kaili University，Kaili，Guizhou 556011，China；2．School of Mathematical Sciences，Kaili University，Kaili，Guizhou 556011，China）

Plasmon excitation in small sodium clusters with triangle structure is studied with time-dependent density functional theory.For relatively larger sodium clusters，along triangle bottom edge and perpendicular bisector of triangle bottom edge，linear shapes of absorption spectra and resonance energies of main absorption peaks are same.However，along these directions，resonance modes of main absorption peaks are different.For the main plasmon mode，field enhancement extrema are located in region of endpoints of the triangle.

plasmon excitation；time-dependent density functional theory；clusters

date： 2013－12－20；Revised date： 2014－04－11

O469

A

2013－12－20；

2014－04－11

国家自然科学基金（11464023），贵州省科学技术基金（LKK［2013］19，LKK［2013］31）及凯里学院课题（Z1308，Z1311）资助项目作者简介：尹海峰（1982－），男，博士，讲师，主要从事纳米材料的等离激元特性研究，E-mail：yinhaifeng1212＠126.com

1001-246X（2014）06-0713-06