贝纳德对流产生的温差条件

齐锦刚， 高 勇， 赵作福， 王家毅， 李 扬， 吴 敌， 王建中

（辽宁工业大学材料科学与工程学院，辽宁锦州 121001）

贝纳德对流产生的温差条件

齐锦刚， 高 勇， 赵作福， 王家毅， 李 扬， 吴 敌， 王建中

（辽宁工业大学材料科学与工程学院，辽宁锦州 121001）

在Boussinesq近似的基础上，忽略贝纳德对流扰动方程二阶和更高阶的扰动，建立速度场和温度场的扰动方程.通过无量纲处理得到控制贝纳德对流的超越方程，利用MATLAB求解超越方程，得到实验室产生贝纳德对流的参数，为贝纳德对流实验提供参考和指导.

贝纳德对流；扰动；耗散结构

0 引言

贝纳德实验在非平衡热力学、非平衡态统计物理和非线性力学中都是一个非常重要的研究课题.连续介质力学中的贝纳德对流是布鲁塞尔学派最早用来说明他们的耗散结构物理图像的典型例子之一［1］，而且在力学中也是混沌现象的代表性实验［2］.国内外不少文献对其实验和产生的非线性理论作了定性描述［3－4］.近年来有国外学者在Boussinesq假设下从理论上初步研究了三维情况下，温度场和磁场对贝纳德对流的扰动，并建立了温度场和磁场的扰动方程［5］.有学者以三维圆柱体腔体为模型，在不同瑞利数下对贝纳德对流热耗散率作了统计分析，得出无量纲数之间的标度律关系［6］.

八十年代，Libchaber研究组提出了混合理论［8］.该理论认为腔体内的液体分为三个区域.并认为冷热羽流从上下温度边界层产生，在混合区域内合并，然后进入中央区域内.当上下温差达到一定的临界值时，液体会出现平稳的、类似以六边形的对流翻滚状态.在六边形的中心液体向上流动，六边形的边缘，液体向下流动.

Gertsenshtein，Zheligovsky基于Boussinesq近似，研究了三维腔体中平面薄层液体在外场扰动下的理论.但是没有得到试验验证.尽管混合理论对贝纳德对流现象的定性解释比较完美，但是未能实验验证.在1991年，有研究认为贝纳德对流与瑞利流不同，不是浮力而是表面张力的作用［11］.这使人们对混合理论产生了疑问.1997年Ning，Yoshifumi，Hideo认为贝纳德对流是非线性科学中的一个重要的模型，具有实验简单并且易于控制的优点，支配方程比较明确，于是将其作为研究非线性科学的重要课题［12］.1999年王晋军等人认为，存在的问题是硬湍流是否为Benard对流的极限状态［7，9］.

在近十年来对贝纳德对流的研究相当活跃.学者们从自组织结构出发，认为当温度梯度达到一临界值时，静止的液体出现了许多规则的六边形，在元包中心液体向上运动，边缘液体向下运动，这时液体内分子出现宏观有序组织［10－15］.

国内学者利用贝纳德对流现象的产生对地震进行预测［7］，也有学者利用贝纳德对流原理分析冰雹的产生和预测［8］取得了初步模型的成功.这些研究对从理论到实验的过度和跨越有一定参考价值.但定量上讨论贝纳德对流的稳定性和产生条件等问题则报道较少.本文在Boussinesq近似的基础上，忽略贝纳德对流扰动方程二阶和更高阶的扰动，建立速度场和温度场的扰动方程，通过对变量的无量纲处理得到控制贝纳德对流的超越方程，最后利用MATLAB对超越方程进行求解，得到实验室产生贝纳德对流现象的温差参数，探讨贝纳德系统的产生机理.

1 贝纳德对流的物理模型

如图1所示，在直角坐标系Oxy中，有一立方体腔体，格线表面分别是上下固定表面，用来保持一定的温度梯度.周围四个面是绝热面，与外界没有任何热传递.腔体中充满液体.从下固定边界加热，上表面保持温度不变.由于液体的上层温度T2低于液体的下层温度T1，下层液体受热膨胀，密度减小，在浮力的作用下向上层运动，与此同时上层液体向下运动，由于液体具有粘性，这些运动会受到液体粘滞力的阻碍.当温差ΔT＝T1－T2较小的时候，由温差产生的浮力不足以克服粘滞力的作用，液体静止不动，呈现典型的静态热传导过程．当下部继续加热，温差ΔT大于某个值时，将出现一种平稳的类似六角形的对流翻滚状态，在六角形的中心流体向上运动，边缘流体向下运动.

图1 贝纳德对流实验模型Fig.1 Experimental model for Benard convection

2 贝纳德对流方程

2.1 温度梯度

分析模型条件可以看出，立方体腔体内温度只沿z方向变化，是一维稳态导热，导热过程可用导热微分方程描述

根据假设简化成

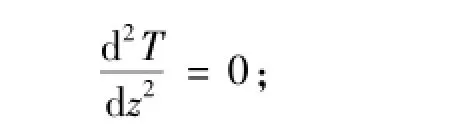
边界条件为z＝－1／2，T＝T1，z＝1／2，T＝T2．对上式积分带入边界条件得出沿z方向的温度分布为

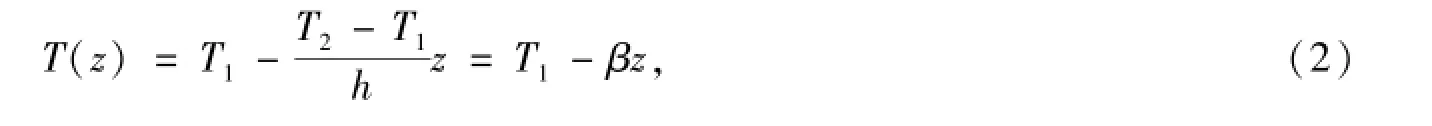
其中.β为温度梯度，h为上下液层厚度.

2.2 流体运动的动力学方程

1）动量守恒方程

其中，πij＝ρuiuj－σji为动量通量张量，σij＝σji，为应力张量［9］，f为单位质量力，u为速度矢量，ρ为液体密度.

采用Boussinesq近似［10］密度ρ＝ρ0［1＋α（T1－T）］，其中：α为热胀系数，T1为腔体下底板的温度，T为Z方向上任一高度的温度，ρ0为加热时下底板的密度.

2）能量守恒方程

其中，e为单位质量流体的内能，de＝cVdT，cV为体积比热容；σ：∇u为两个张量的双点积；Q表示有辐射或化学能释放等因素而产生的系统内单位体积内流体热量的增量；q为热通量向量，前面的负号表示热量进入系统，否则就是热量从系统散失.

在不可压缩和Boussinesq近似的条件下，能量守恒方程可改写为

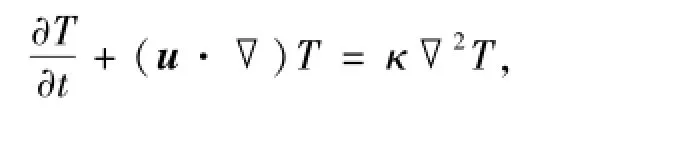
其中，κ＝λ／（ρ0cV）为热扩散率，λ为导热系数.

考虑速度、温度分布的扰动，忽略扰动的非线性项之后，以上两动力学方程可写为

其中，θ为温度的扰动变化量，ω为速度的扰动变化量.

2.3 外场扰动方程

通过前面的描述，必须用一套完整的模型去分析任意扰动对贝纳德稳定性的影响.鉴于此，建立了二维周期波的扰动函数模型［10］，如此，描述贝纳德对流的扰动就是依赖于x，y和时间t，扰动的表达式

其中，k是扰动的波数，p是一个常数.

根据以上扰动模型，我们不难建立速度场ω，温度场θ对贝纳德对流的扰动函数表达式

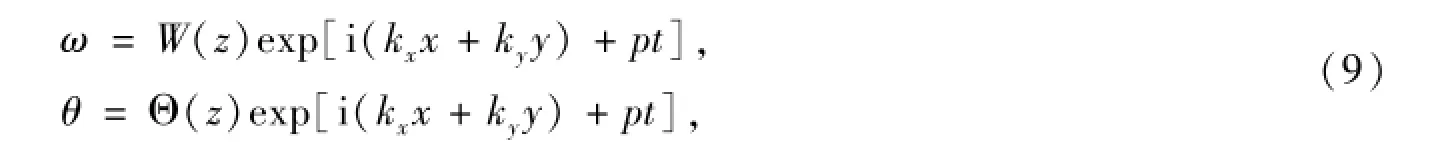
为了简化问题，设

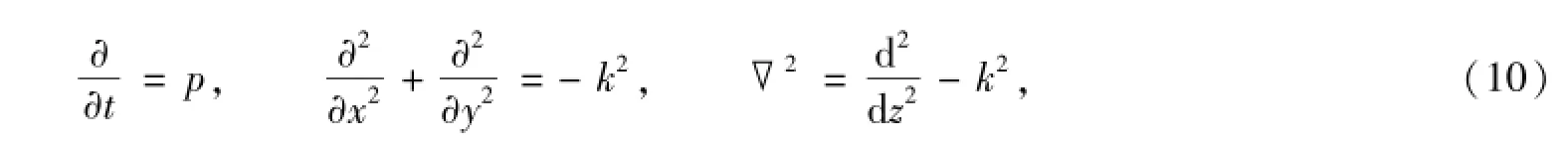
将其代入方程（5）、（6），可得

为了讨论问题的方便，进行无量纲化处理，令

其中，a表示波数，σ表示时间常数.然后将其带入方程（11）、（12）得

其中方程（15）右边的gαβd3／（νκ）便是瑞利数R，即R＝gαβd3／（νκ）．

通过证明得，对于所有的正的瑞利数R，常数σ都是实数［10］，所以贝纳德对流从稳定到不稳定的发生肯定是通过一个定态产生的．因此，边缘方程肯定是通过σ＝0产生的，于是将σ＝0带入方程（13）、（14）可得

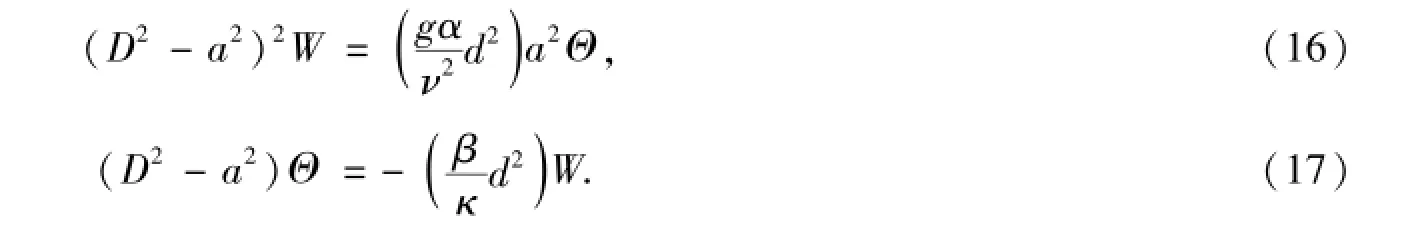
通过方程（16）、（17）分别消去Θ，W得

3 临界方程

为求解建立的模型方程，须寻求合适的边界条件.本文中，由于立方体腔体中上下表面都是固定表面而且对称，为解决问题的方便，建立如图2所示的坐标系，此时液体在z＝±1／2之间.

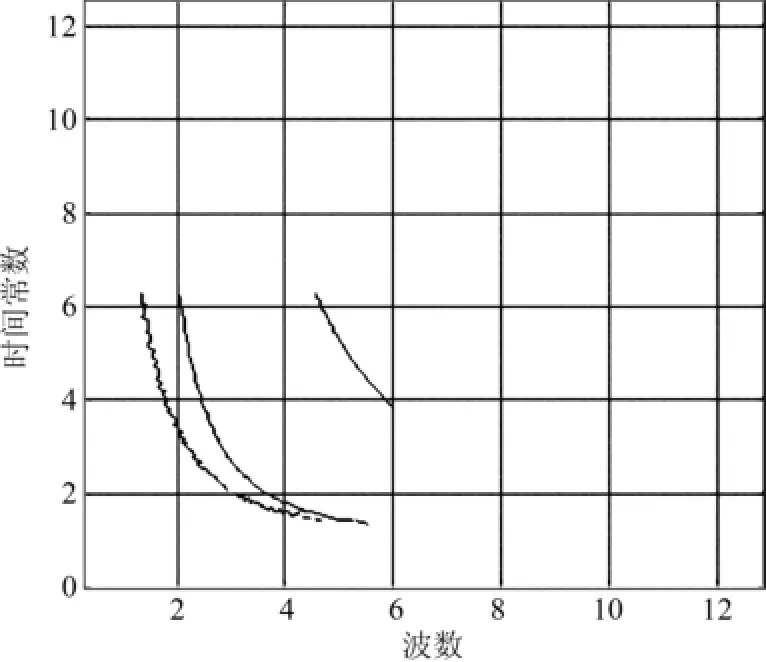
图2 时间常数随波数变化的MATLAB曲线Fig.2 MATLAB curves of wave number changes with time constants

为解方程（18），根据实际情况建立以下边界条件

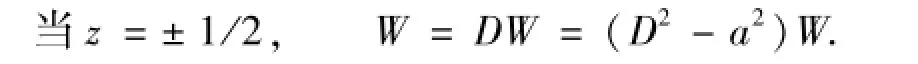
通过观察方程和z＝±1／2时，边界条件的连等式，发现方程（18）的解应该是两个不相联系的奇偶解，把方程（18）的解表示为

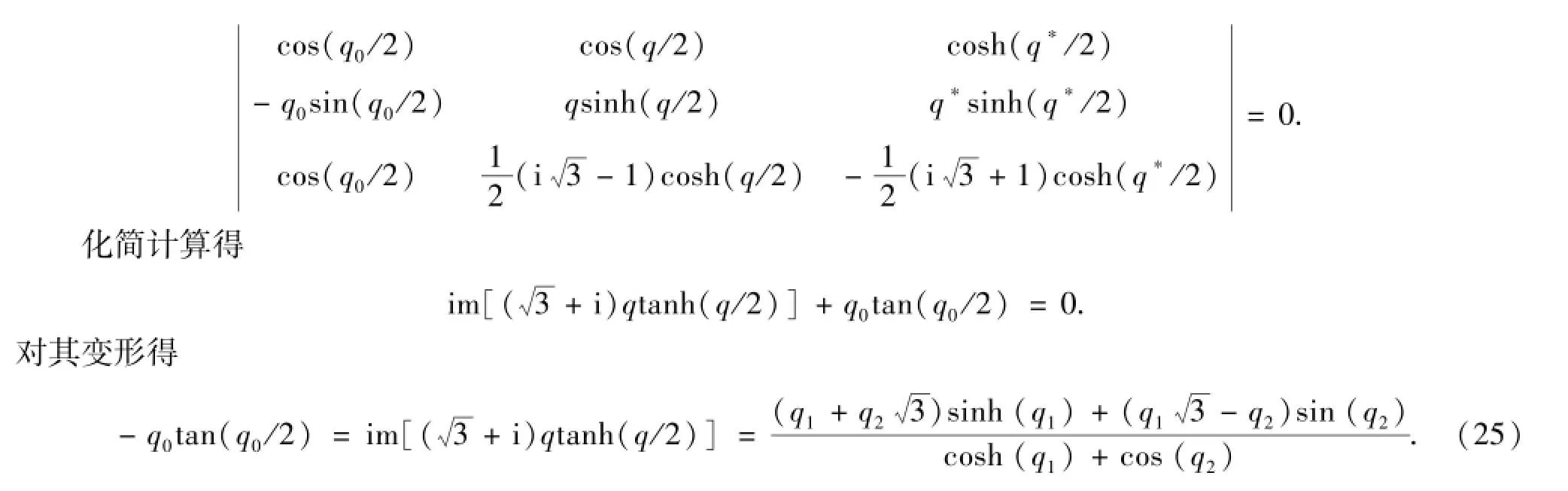
其中q0，q1，q2是关于波数a和时间常数 的表达式，即方程（25）是一个关于a和 的函数，又因为通过方程（22）得： ＝（R／a4）1／3，所以方程（25）是关于波数和瑞利数的一个函数.通过MATLAB软件［11］可求出R的临界值RC≈1 700.

当R＞RC时贝纳德对流产生．根据方程（15）得出的瑞利数为R＝gαβd3／（νκ）．其中：g为重力加速度；α为热膨胀系数；β为上下表面的温差；ν为运动粘度；κ为热扩散系数．本文通过各物性参数［12］，计算得出了以下两种液体作贝纳德对流实验所需要的温差β.

表1 硅油贝纳德实验的参数Table 1 Parameters of Benard experiments with silicone

表2 水贝纳德实验的参数Table 2 Parameters of Benard experiments with water

表3 润滑油贝纳德实验的参数Table 3 Parameters of Benard experiments with lubricating oil

4 结论

通过以上方程，得出了以下结论：

1）贝纳德对流现象可以在Boussinesq假设的基础上通过动量守恒方程，内能守恒方程来描述，外场对贝纳德对流的扰动能够用二维周期波函数来建立.

2）贝纳德对流从稳定到发生对流的过度可通过临界瑞利数来判断.

3）以硅油、水和润滑油为例计算出在实验室完成贝纳德实验需要的参数.

［1］ Li Rusheng.Non-equilibrium thermodynamics and dissipative structure［M］.Beijing：Tsinghua University Press，1986.

［2］ Chang Shuren，Lv Kecheng.Elementary introduction about the“chaos”［J］.University Physics，1999，18（11）：36－37.

［3］ Zhao Kaihua.From the pendulum to chaos［J］.Knowledge of Modern Physics，1994，6（1）：42－45.

［4］ Schuster H.An introduction to the science of chaos［M］.Chengdu：Sichuan Education Press，1994.

［5］ Gertsenshtein S Ya，Zheligovsky V A，et al.Hydromagnetic dynamo and stability of three-dimensional convective flows in a horizontal layer of a solution［J］.Eur J Opl Res，1989：302－313.

［6］ Mohammad SEmran，Jorg Schumacher.Conditional statistics of thermal dissipation rate in turbulent Rayleigh-Benard convection［J］.Eur J Phys J E，2012，35：108.

［7］ Hai Yanhe.Bernard effect and earthquake prediction［J］.Journal of Xi'an Institute of Mining，1990，10（3）：18－19.

［8］ Zhao Wentong，Zhao Peizhang，Teng Xiao，et al.Hail forecast and prevention［J］.Xinjiang Meteorological，2005，28（1）：1－2.

［9］ Zhang Zixiong，Dong Zengnan.Viscous fluid mechanics［M］.Beijing：Tsinghua University Press，1998：23－25.

［10］ Chandraskhar S.Hydrodynamic and hydromaynetic stability［M］.New York：Dover，1961：25－40.

［11］ Lin Xuesong，Zhou Qian，Lin Dexin et al.The application of MATLAB7.0［M］.Beijing：Machinery Industry Press，2006.

［12］ Dai Guosheng.Heat transfer［M］.Beijing：Higher Education Press，2009：322－326.

［13］ Zhou Quan，Xia Keqing.Present situation and prospect of progress Rayleigh-Benard turbulent heat convection study［J］. Advances in Mechanics，2012，42（3）：231－250.

［14］ Wang Jinjun，Xia Keqing.The effects of Reynolds number on turbulence［J］.Mechanics and Practice，1999：21（6）：1－2.

［15］ Huang Dinghua，Ye Junlin.Deep convection and plate motion［J］.Geological Science and Technology Information，1991，10（3）：7－8.

［16］ Ning Lizhong，Yoshifumi Harada，Hideo Yahata.Formation process of the traveling wave state with a defect in binary fluid convection［J］.Progress of Theoretical Physics，1997，98（3）：555－560.

［17］ Li Guodong.Traveling-wave patterns in binary mixtures convection with through flow［J］.Progress of Theoretical Physics，2001，106（2）：294－300.

［18］ Ning Lizhong，Yoshifumi Harada，Hideo Yahata，et al.Transition of convection patterns in a rectangular cell［J］.Journal of Hydrodynamics，2001，B13（4）：60－75.

［19］ Kadanoff L P.Turbulent heat flow：Structure and scaling［J］.Physics Today，2001，54（8）：34－39.

Temperature Conditions of Bénard Convection

QI Jingang，GAO Yong，ZHAO Zuofu，WANG Jiayi，LI Yang，WU Di，WANG Jianzhong
（School of Material Science and Engineering，Liaoning University of Technology，Jinzhou 121001，China）

Disturbance equations of velocity and temperature fields are built based on Boussinesq approximation，in which second order and higher-order disturbance of Bénard convection are ignored.Transcendental equations controlling Bénard convection are obtained with non-dimensional treatment of variables.Specific parameters of Bénard convection are obtained，which provide reference and guidance for Bénard convection experiments.

Bénard convection；disturbance；dissipative structure

date： 2013－12－24；Revised date： 2014－04－10

N34

A

2013－12－24；

2014－04－06

国家自然科学基金（51074087，51354001）；辽宁省自然科学基金（201102088）及辽宁省高等学校杰出青年学者成长计划（LJQ2011065）资助项目

齐锦刚（1973－），男，博士，教授，研究方向为冶金熔体科学，E-mail：qijingang1974＠sina.com

1001-246X（2014）06-0675-06