高温高压条件下堆积颗粒的吸能效应

王宏亮， 田 宙， 郭永辉

（西北核技术研究所，陕西西安 710024）

高温高压条件下堆积颗粒的吸能效应

王宏亮， 田 宙， 郭永辉

（西北核技术研究所，陕西西安 710024）

建立二维轴对称气固两相双流体物理模型.对三种不同源区初始质量比内能E0／10、E0／100、E0／1 000，固体堆积颗粒作用下气相流场能量、压力衰减进行数值模拟.结果表明：初始质量比内能越高，堆积颗粒作用下流场动能、内能衰减越快；初始质量比内能越高，流场压力衰减达到准静状态的速度越快，准静态后压力衰减也越快.

高温高压；双流体模型；有限体积方法；堆积颗粒；能量衰减

0 引言

爆炸实验中，在激波传播路径上，适时喷洒粉尘抑爆剂，或提前设置堆积颗粒，可达到衰减激波，抑制爆炸的目的［1－8］.目前，关于粉尘或堆积颗粒抑爆问题所开展的实验和数值研究中，重点关注的基本是堆积颗粒或悬浮粒子的动力学行为对冲击波载荷的影响，而未对高温条件下，堆积颗粒吸热效应对于流场能量及冲击波载荷的影响进行细致研究.

高温高压环境下，气相流场与固相颗粒通过热传导、辐射传热机制进行热量传递，当固相颗粒温度达到熔点、沸点时发生相变，从而可能向气相流场传递质量.理论上，单位时间内球形颗粒表面通过对流换热同周围流体之间的传递的热量同两者的温差成正比，而以辐射方式彼此传递的热量同两者温度四次方的差成正比，这里固相温度指其表面温度，温度越高，热量传递效率越高，辐射传热较对流传热的影响也会越来越重要，会对流场冲击波载荷造成影响.

利用高温高压多相流体动力学已有研究成果，建立二维轴对称气固两相双流体物理模型，并设计高效非结构有限体积数值计算方法对模型进行数值求解，用所建立的方法成功对具体实验条件下沙墙消波吸能效应进行数值研究，计算结果表明：冲击波到时、容器内准静气压数值计算结果同实验结果符合良好，验证了所建物理模型及计算方法解决高温高压条件下堆积颗粒吸能物理问题的合理性［9］.应用上述数值算法，设定不同等温等压源区条件，对颗粒吸能效应进行数值模拟，对比分析不同初始质量比内能条件下，气相能量衰减以及流场压力时间历程.结果表明：源区相同能量、压力，不同质量条件下，温度不同时，堆积颗粒作用下流场能量衰减速率、冲击波载荷衰减速率存在很大的差异，气固热交换是影响流场压力变化的重要因素，且源区初始质量比内能越小，影响越突出.

1 物理模型

高温高压条件下，气流同堆积颗粒的相互作用机理为：一方面，堆积颗粒在激波作用下快速飞散，导致部分流场能量转变为颗粒动能；另一方面，颗粒在高温气流冲刷下升温，可能熔化、汽化，部分流场能量转变为颗粒内能；此外，颗粒在高速气流冲击下可能破碎细化，消耗部分流场能量，细化颗粒会进一步吸收流场能量.

基于连续介质假设，将稠密堆积颗粒当作连续相在Euler坐标系中处理，考虑相间双向耦合作用，基于合理简化，推导气相－固相控制方程.

1.1 基本假定

物理模型基本假定如下：

①不考虑空气粘性；

②不考虑固相粘性，考虑固相分压，固相本构方程基于弹性体假设推导得到；

③考虑气体－颗粒间通过热传导、辐射传热机制所引起的热量传递；

④考虑颗粒受热相变，及汽化引起的质量传递，但假设颗粒为惰性物质，不发生化学反应，图1为颗粒比内能同温度的关系，图中：Qmelt、Qeva代表颗粒熔化热、汽化热.

⑤考虑气体－颗粒间由于速度差，通过阻力作用所引起的动量传递，不考虑颗粒所受重力等；

⑥固相颗粒粒径均匀一致，不考虑粒子破碎过程，固相颗粒粒子数保持不变.

图1 颗粒比内能同温度的关系Fig.1 Specific internal energy of a particle as function of temperature

1.2 控制方程

基于以上假定，气固两相Euler-Euler型二维轴对称控制方程组，

式中，气相、固相控制方程中第一式为质量守恒方程，第二、第三式为动量守恒方程，第四式为能量守恒方程，固相控制方程最后一式为粒子数守恒方程；F代表气相、固相质量、动量、能量、粒子数守恒量矢量；G、H代表气固质量、动量、能量、粒子数沿轴向、径向单位面积对流通量矢量；Ψ代表气固方程右端源项；φ、ρ1、u1、v1、e1、E1、T1、p1分别代表气相单元体积分数、密度、径向速度、法向速度、单位质量比内能、单元总能量、温度、压力；γ代表气相绝热指数；ζ、ρ＾2、u2、v2、e2、E2、T2、p2、N分别代表固相单元体积分数、颗粒材料密度、径向速度、法向速度、单位质量比内能、单位体积总能量、温度、压力、单位体积粒子数目；r、cS代表粒子半径、比热容.

对于固相压力，其表达式称为固相本构方程，是为了描述颗粒碰撞所引起的固相应力，由于不考虑固相粘性，即不考虑固相切应力，仅考虑固相法向应力.关于固相粘度、应力问题，国内外学者提出不同描述方法，如Pritchett（1978）和Lyczkowski（1993）等采用固体弹性模量模型、Ding＆Gidaspow（1990）等所提出的分子动力学模型，以及范宝春等根据激波与堆积粉尘相互作用的实验结果以及斜激波的相关理论所确定的堆积粉尘本构方程等［9］.本文通过弹性体假设提出堆积颗粒本构方程，

式中：K为颗粒材料体积模量；ζ为颗粒堆积体积分数；ζpmax为球形颗粒的最大堆积密度，在实际应用中需参考实验结果进行修正，具体推导过程参见文献［10］.

控制方程右端，除第一项，其余各项分别代表两相质量、动量、热量交换作用，其计算公式如下：

采用Sreznevsky液滴蒸发模型描述气相、固相之间的质量交换式（8），假设固相颗粒为惰性粒子，当其温度达到沸点时，发生汽化，从而向气相流场传递质量.

式中：k代表气体热传导系数；Nu为Nusselt数，Pr为Prandtl数；Re代表Reynolds数；μ1、cp代表气相介质粘性系数及定压比热容.

采用牛顿阻力定律描述高雷诺数条件下气固两相之间的阻力作用式（11）、式（12），阻力系数计算公式见式（13）.

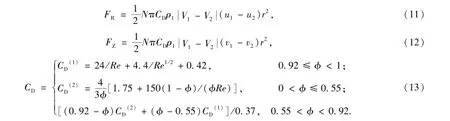
式中：CD为阻力（驱动力）系数；FR、FZ分别为两相介质之间径向、轴向动量交换有关的驱动力项.气固两相之间的热量交换率，

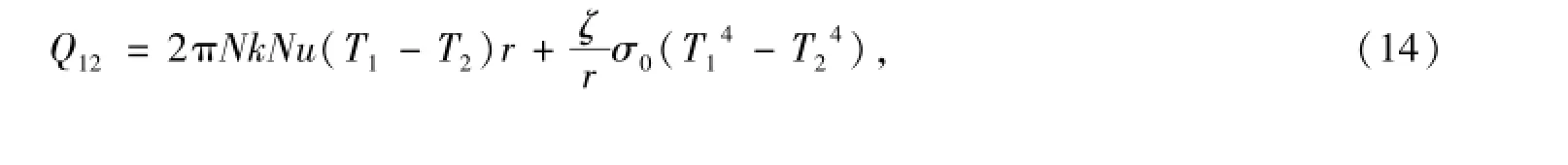
式中，右端第一、第二项分别代表热传导、辐射传热所引起的热量传递；σ0为斯蒂芬－玻尔兹曼常数，其值为5.67×10－8J·（s·m2·K4）－1.

2 堆积颗粒吸能效应

数值研究源区初始体积比内能、压力相同，初始质量、温度不同时，见表1，堆积颗粒作用下流场能量、压力变化规律.

表1 计算条件Table 1 Computational conditions

2.1 计算条件

计算模型如图2所示，约束空间区域半长为20 m，半径1.0 m，堆积颗粒位置如图所示.堆积颗粒为沙粒，初始堆积体积分数约为0.4，沙粒物性条件见表2.计算中，气相为单一空气介质，初始时刻，流场源区处于高温高压状态，源区以外区域气体处于标准状态.

图2 计算模型Fig.2 Computational model

表2 沙粒物性条件Table 2 Physical and thermodynamical parameters of sand particles

2.2 计算结果

根据以往研究，冲击波与堆积颗粒相互作用过程中，堆积颗粒，一方面在冲击作用下发生挤压，透射波过后，堆积颗粒自自由表面层层发生飞散运动；另一方面，在波后气流作用下，其速度、温度会不断增大.而冲击波在堆积颗粒作用下，会发生反射、透射、绕射等物理现象.因此，在冲击波与堆积颗粒相互作用过程中，冲击波对堆积颗粒做功，其载荷降低，传播速度降低，即流场动能向堆积颗粒进行了转移；另外，由于波后气流与堆积颗粒之间仍然存在速度差、温差，因此在作用过程中，流场动能、内能会不断向堆积颗粒进行转移，从而造成流场总能量衰减.

图3为t＝0.05 ms时刻，三种计算条件下，流场压力等值云图，如图所示：源区初始能量、体积相等时，源区质量越小，源区膨胀所产生首道冲击波传播速度越快，当然波后介质速度也更快.图4为t＝1.0 ms时刻，三种计算条件下，流场压力等值云图，从图中可以看出：冲击波在堆积颗粒作用下，发生明显绕射现象.

图5、图6、图7为三种计算条件下，气相总能量、总动能、总内能随时间变化，显然：源区初始体积比内能相等时，源区质量越小，气相总能量、总动能、总内能衰减越快；源区初始体积比内能相等时，源区质量越大，源区总能量转化为气相动能的比例越大，但三种情况下，气相以动能形式衰减的能量不超过气相总能量的20%，大部分能量将以热能的形式被颗粒吸收.源区质量等于10 kg、100 kg、1 000 kg时，气相总能量趋于平衡的时刻分别为1 ms、几十ms、百ms.从图中可以看出，气相总能量与总内能变化趋势一致，气相总内能趋势变化，决定流场达准静态后压力衰减趋势.也就说明，源区初始体积比内能相同时，质量越小，冲击波载荷衰减达准静态后压力衰减速率越快.图8、图9为三种计算条件下，约束空间壁面Z＝0.0 m、6.21 m处，压力随时间变化曲线，如图所示：质量越小，冲击波脉宽越窄，传播速度越快，激波衰减速率也越快，即：流场内能衰减对于激波衰减的影响也越大.

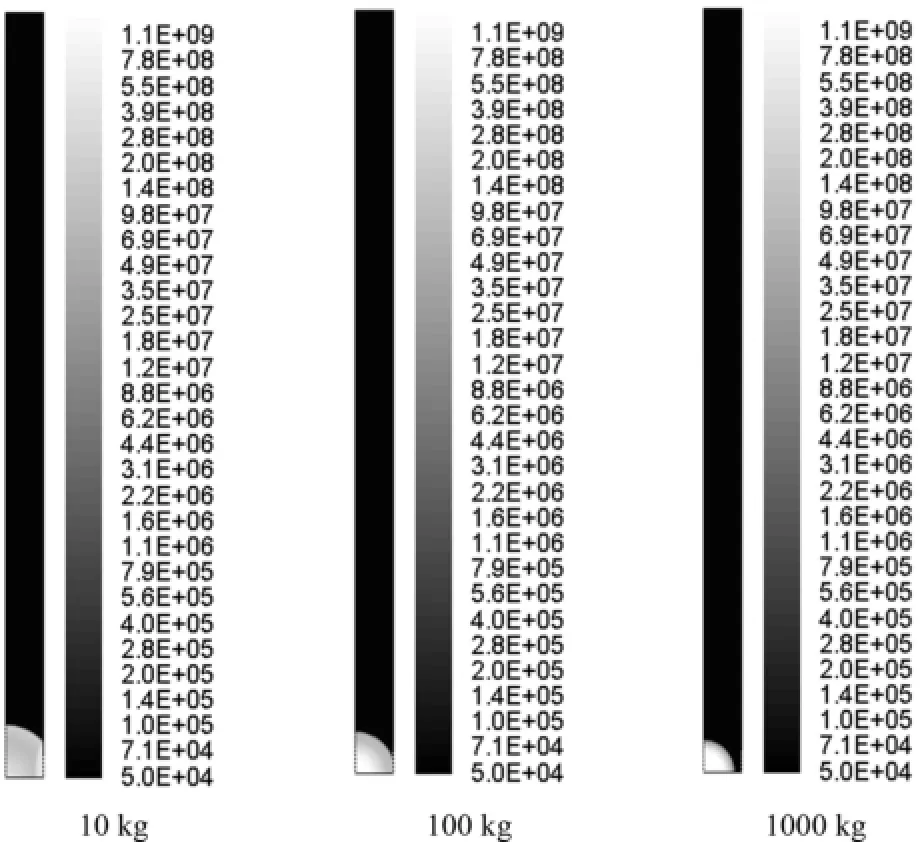
图3 三种计算条件下，t＝0.05 ms时刻，压力云图Fig.3 Pressure contours at t＝0.05 ms under conditions in Table 1

图4 三种计算条件下，t＝1.0 ms时刻，压力云图Fig.4 Pressure contours at t＝1.0 ms under conditions in Table 1

图5 三种计算条件下，气相总能量随时间变化Fig.5 Ratio of gas total energy to E0 under conditions in Table 1

图6 三种计算条件下，气相动能随时间变化Fig.6 Ratio of gas kinetic energy to E0 under conditions in Table 1

图7 三种计算条件下，气相内能随时间变化Fig.7 Ratio of gas internal energy to E0 under conditions in Table 1

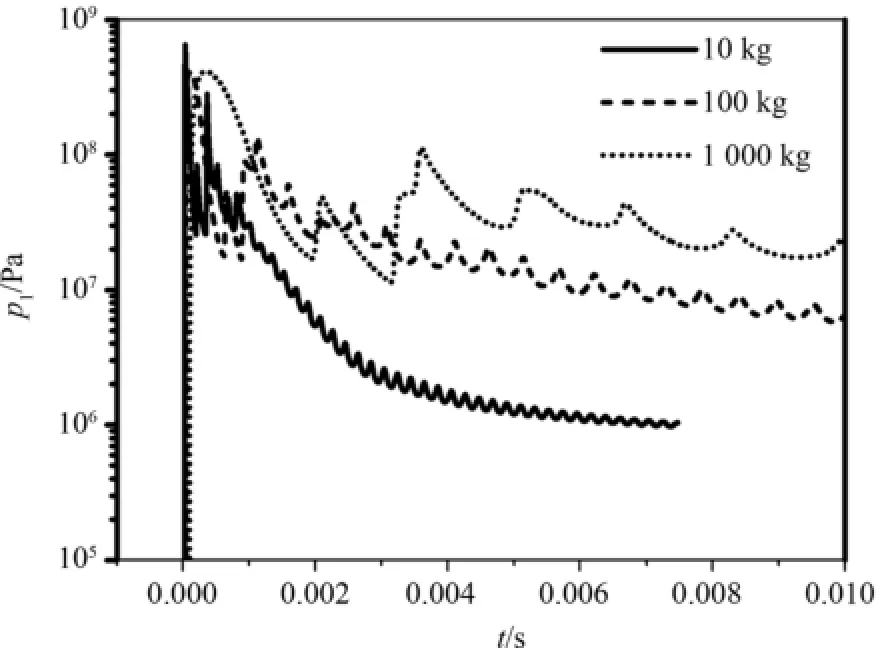
图8 三种计算条件下，约束空间壁面z＝0.0 m处压力随时间变化Fig.8 Pressure vs.time at z＝0.0 m on wall of computational model under conditions in Table 1

图9 三种计算条件下，约束空间壁面z＝6.21 m处压力随时间变化Fig.9 Pressure vs.time at z＝1.0 m on wall of computational model under conditions in Table 1

3 结论

通过上述研究，当三种源区条件能量相同、体积相同，气相采用一种状态方程描述，压力相同，可以得到以下结论：

1）不超过20%源区能量以动能形式发生衰减，即大量源区能量将以热能形式发生衰减；

2）气相动能衰减速率，决定了流场达准静态的时刻.气相流场初始质量比内能越高，冲击波脉宽窄，传播速度快，造成固相颗粒作用下气相动能衰减越快，流场达到准静态越快.

3）气相内能衰减速率，决定了流场达准静态后压力衰减的快慢.初始质量比内能越高，气相总内能衰减越快，流场达准静态后压力衰减也越快.也就表明：气固两相之间热量交换，对于流场压力变化具有重要影响，且初始质量比内能越高，这种影响越显著.

［1］ Fan Baochun，Xie Bo，Zhang Xiaohe，et al.Experimental research on explosion suppression by inert particles［J］. Experiments and Measurements in Fluid Mechanics，2001，15（4）：20－25.

［2］ Fan Baochun，Li Hongzhi.Numerical simulations of explosion suppression by inert particles［J］.Explosion and Shock Waves，2000，20（3）：208－214.

［3］ Xie Bo，Fan Baochun.Study on active explosion suppression by powder in large-scale duct［J］.Chinese Journal of Applied Mechanics，2010，27（2）：280－286.

［4］ Zhang Lite，Shi Honghui.Reflection and transmission mechanism of shock wave interacting with moveable particle group［J］. Journal of China Coal Society，2010，27（2）：280－286.

［5］ Zhang Dezhi，Zhong Fangping，Ma Yanjun，et al.Experimental investigation on explode loading of the slender cylindrical vessel［C］.8th Symposium on Shock＆Impact Dynamics Yinchuan，China，2007.

［6］ Cui Yunxiao，Hu Yongle，Chen Jianjie，et al.Numerical simulation for explosive test in explosion containment vessel filled with sand［C］.9th Symposium on Shock＆Impact Dynamics，Jiaozuo，China，2009.

［7］ Yu Yong，Zhang Xia，Chen Wei.Simulation of supersonic gas-particle two-phase flow with two-fluid model［J］.Journal of Aerospace Power，2010，25（4）：800－807.

［8］ Lei Ming，Zhang Baihua，Wang Hongliang，et al.Numerical simulation of effect of energy absorption of sand walls under blast wave［J］.Journal of PLA University of Science and Technology，2007，8（5）：434－438.

［9］ Wang Hongliang，Tian Zhou，Guo Yonghui.Numerical study of effect of sand-walls on shock wave attenuation［C］.1st National Conference on Explosion Vessel，Sichuan，China，2010.

［10］ Wang Hongliang，Tian Zhou.Deduction of constitutive equation of granular materials based on plastic theory［C］.Advances in Computational Explosion Mechanics，Qingdao，China，2006.

Effect of Particles-piled on Energy Attenuation at High Temperature and High Pressure

WANG Hongliang， TIAN Zhou， GUO Yonghui
（Northwest Institute of Nuclear Technology，Xi'an 710024，China）

Two-dimensional axi-symmetric gas-solid two-fluid model was established.Under three conditions of source：E0／10，E0／100，E0／1 000（initial energy per mass of gas），diminishing of gas energy and gas pressure caused by packing particles was studied.It shows that：With higher initial energy per mass of source kinetic and internal energy of gas is diminished by packing particles more quickly，gas fluid is close to stillness more quickly，gas pressure is decreased more quickly.

high temperature and high pressure；two-fluid model；packing particles；energy attenuation

date： 2013－11－26；Revised date： 2014－04－25

O359

A

2013－11－26；

2014－04－25

王宏亮（1983－），女，硕士，主要从事两相流研究，E-mail：wanghongliang＠nint.ac.cn

1001-246X（2014）06-0706-07