磁偶极子远场的严格数学处理
2014-06-09刘国松
刘 莹,刘国松
(长春工程学院理学院,长春130012)
0 引言
电偶极子和磁偶极子是介质电磁属性描述和研究的重要模型。相对而言,磁偶极子模型的处理和应用远较电偶极子复杂,原因主要在于磁场的无(散度)源、有旋性。电、磁偶极模型在普通物理课程中均以典型例题的面目出现在教科书和教学过程中[1],却没有深入阐述其对于介质电磁场研究的重要性,更谈不上在介质场处理中的应用。
由于介质场对势函数的贡献归根结底来源于电、磁偶极子,即分子偶极矩,而分子尺度在连续介质理论中相对于连续介质微元总可以认定为充分小量,所以无论是电极化强度,还是磁化强度,都可以用大量偶极矩贡献的宏观平均描述,故而远场表达是很好的重要近似。
对于磁偶极子远场的计算,众多教科书中都有涉及[2]。通行的处理方法是将给定半径的载流圆环置于欧氏空间的x-y平面且使其环心与坐标原点重合,在z-x平面上选取任意充分远点,采取一阶近似,得到远场表达式,再利用偶极子场关于z轴的对称性,得到空间任意远点偶极场[3],最后一步推广到磁偶极子位于空间任意位置、偶极矩空间指向任意情形下,距其充分远点磁矢势的严格表达。这种方法虽然得到了可靠的结果,但是操作过程复杂,而且从数学上来说是不严格的。
下文首先对通行处理做一简要回顾,然后再介绍严格的处理过程。
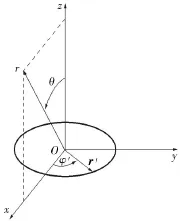
图1 磁偶极子远场一般处理模型
如图1所示,选回路中心为球面坐标的原点,有关源坐标的物理量是带撇的。在此情况下,可做某些近似计算。考虑体系具有轴对称性,对称轴为z坐标轴,显然磁矢势的模与场点的角位置φ无关,为了方便,在z-x平面内选取任意远点进行磁矢势计算。在载流环上选取任意载流微元Idl′=Iadφ′eφ,其对场点的磁矢势贡献为
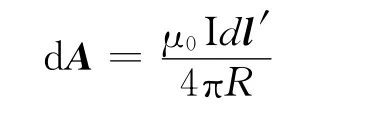
因此,场点处的磁矢势为
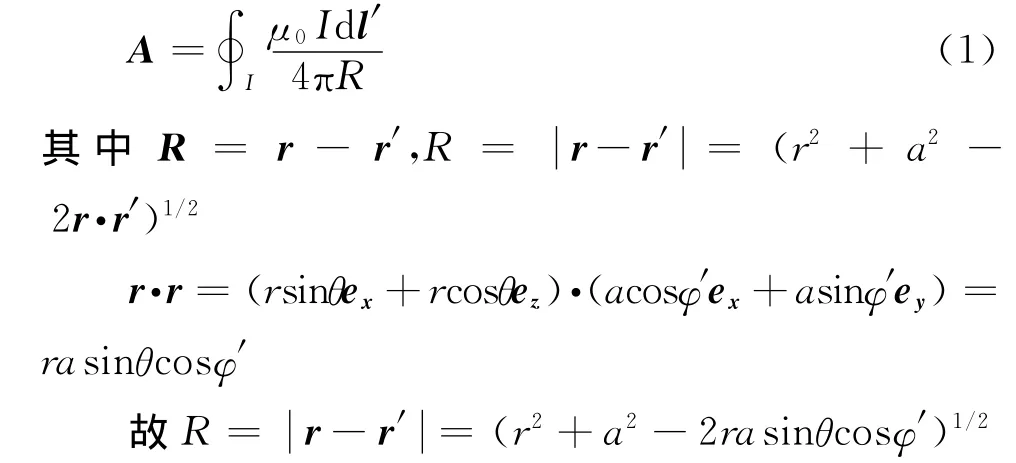
利用远场条件,r>>a,进行如下泰勒级数展开得到:
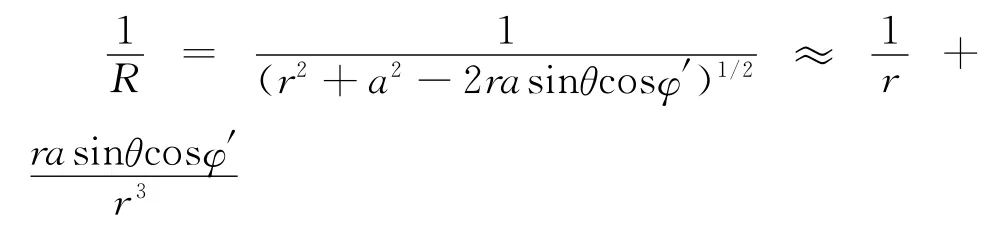
对于任意载流微元Idl,都存在与其对称的微元,它们对磁矢势的贡献在x方向相互抵消。这里需要注意:矢量积分过程中方向的判断问题。所以
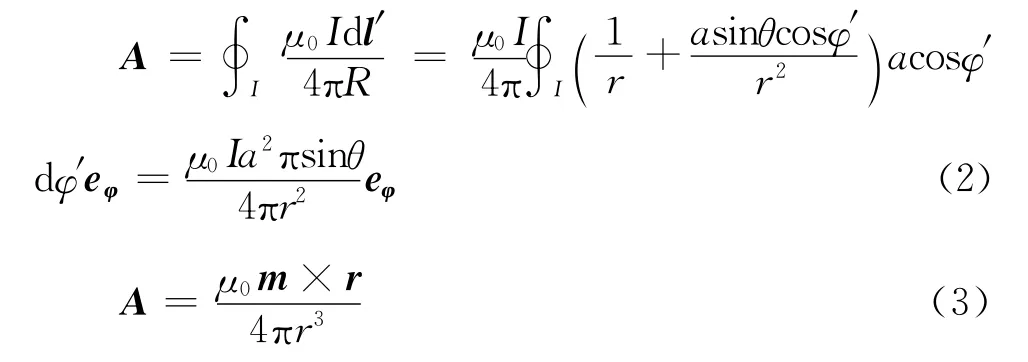
该处理过程虽然得到的结果是正确的,但是推理过程严格性存在缺陷。严格的处理应当将磁偶极子置于坐标系中的一般位置、偶极矩指向任意,且场点选择任意。另外从球坐标表达式(2)到矢量乘积表达式(3)的过渡处理过程难以令人信服。
1 磁偶极子远场的严格处理
载流环位于欧氏空间任意位置,其环心位置矢量为r′,以该矢端为参考点的载流微元相对位矢为r″,远场点位矢为r,则任意载流微元Idr″的位置矢量为r′+r″,如图2所示。
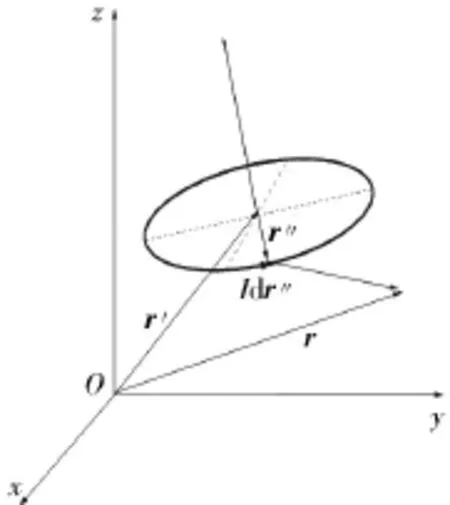
图2 磁偶极子远场严格处理模型

进行一阶展开得到
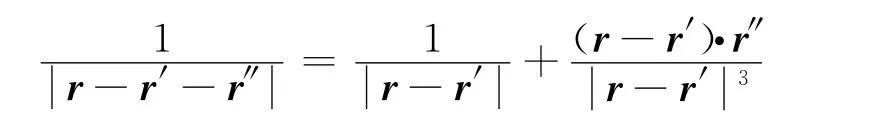
则根据式(1)矢势微元

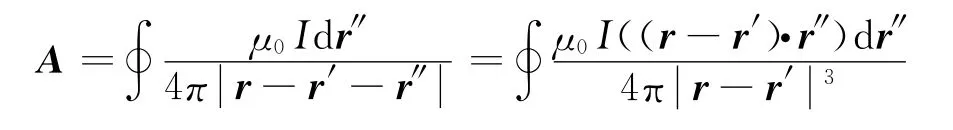


根据矢量运算恒等式
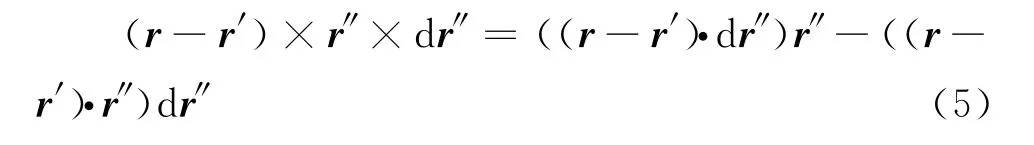
故而

所以

这样就在坐标系无关的前提下得到了磁偶极子远场的严格表达式。
2 磁偶极子远场结论的重要地位
正如同在电介质静电场中电偶极矩有着重要地位一样[4],在描述和研究磁介质磁化机理以及计算介质磁场时,磁偶极子模型是不二选择,不仅使问题得以简化,而且形象易懂,表达严格[5]。介质的磁化源于磁场对电子运动的作用,电子有两种基本运动方式,一是轨道运动,二是自旋。无论哪种运动都可以用一个等效磁矩(分子磁矩)来描述。普通介质(顺磁质、抗磁质)在没有外场条件下,每个分子磁矩的空间指向具有随机性,全部分子磁矩的矢量和为0,对空间任意一点的磁矢势贡献抵消,从而不呈现宏观磁属性;在外磁场当中,无论是抗磁质,还是顺磁质,分子磁矩的空间排布都将具有倾向性,从而净磁矩不为0,空间一般点的总磁矢势贡献不为0,介质呈现磁属性。因而磁介质的磁化程度,完全可以用净磁偶极矩密度刻画。据此,在宏观充分小(刻画空间各点)、微观足够大(磁偶极子足够多,取平均,结果更可靠)的介质区域内将全部磁偶极矩矢量加和,除以该体积微元的体积,得到单位体积内的平均磁偶极矩,它可以准确地描述介质受外场的影响程度,此即为磁化强度[6]。

而且对于任意介质微元dV,其净磁偶极矩可以用磁化强度M(r′)和体积微元dV之乘积表达,如图3所示,它实际上就是一个磁矩为M(r′)dV的磁偶极子。依据上述推理结果,直接得到该“磁偶极子”对空间一点的磁矢势贡献
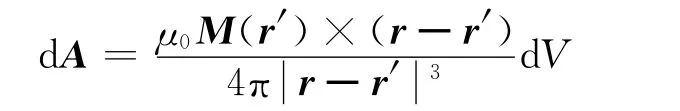
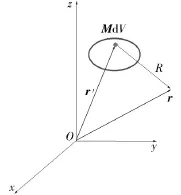
图3 磁偶极子模型在磁介质场中的应用
依据磁化强度空间分布函数进行积分,就可以得到空间磁矢势分布的介质贡献。
实际上,磁偶极模型不仅是磁介质场研究的基础模型,也是宏观复杂载流体的分解模型。兹以图4中的简单载流体为例予以简单说明。图中的平面矩形闭合回路长为a,宽为b,则其总磁矩为Iab,矢量表达为

显然可以将该回路按如图4方式无穷剖分,由于每相邻子回路的边界积分抵消,故而
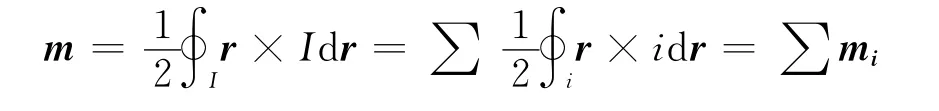
因而宏观导体闭合回路仍然可以用磁偶极子模型(分解)表达。
需要指出分解表达可以在以载流闭合回路为边界的任意单通开曲面上进行,这是由旋量场的属性决定的。由于无穷剖分下的偶极微元可以是任意形状的矢量微元,在前述严格处理中采用了圆环偶极子模型。

图4 磁偶极模型的宏观导体回路应用
3 结语
本文先采用严格的数学推理,给出了磁偶极子远场的数学表达形式。较为详细地讨论了磁偶极子远场模型在磁学研究分析中的基础地位,为电磁场理论的教学和研究工作提供了一种借鉴思路。
[1]赵近芳.大学物理学[M].北京:北京邮电大学出版社,2011:6-7.
[2]Cheng David K.电磁场与电磁波[M].北京:清华大学出版社,2013:162-164.
[3]叶齐政,陈德智.电磁场教程[M].北京:高等教育出版社,2012:158-160.
[4]欧阳金华.介质极化教学的几个问题[J].电气电子教学学报,2008,30(2):1-3.
[5]李静.微小电流环与磁偶极子[J].重庆师范大学学报,2010,27(4):1-3.
[6]赵凯华.电磁学[M].北京:高等教育出版社,1985:551-552.
