某露天开采矿场岩质边坡稳定性分析

2014-06-09唐川，周飞

长春工程学院学报（自然科学版） 2014年2期

唐川，周飞

（成都理工大学地质灾害防治与地质环境保护国家重点实验室，成都610059）

0 引言

岩质边坡稳定性分析一直是岩土工程领域重要的研究课题，并在工程实践中占据相当重要的地位。由于岩质边坡的岩体具有一定的结构特征，不同类型的结构面及其空间的分布状况将决定岩质边坡的破坏模式[1]，因此在对岩质边坡进行稳定性分析之前必须弄清楚岩质边坡中岩体的结构特征。在中国西部山区，天然或人类工程活动等形成了大量的岩质边坡，其破坏程度往往对周围地区人民的生命和财产造成严重的威胁。

目前国内外对岩质边坡的分析研究主要采用现场调查、模型试验、数值模拟和理论分析等方法。连镇营等[2]采用强度折减有限元法对开挖边坡的稳定性进行了研究，其结构表明当折减系数达到某一数值时，边坡内一定幅值的广义剪应变自坡底向坡顶贯通，认为边坡破坏，定义此前的折减系数为安全系数，和强度指标相比，弹性模量、泊松比、剪胀角和侧压力系数对边坡的安全系数影响不大。陆晓敏等[3]引入弹黏塑性流变模型来分析裂隙岩质边坡的变形及稳定性，以块体元模型来反映裂隙岩体变形的不连续性，在单元之间引入接触面单元来模拟岩体中的结构面，在接触面单元中引入弹黏塑性模型来研究岩体变形的时间效应及稳定性。雷远见等[4]将离散元与强度折减法相结合，对含多结构面的岩质边坡的稳定性进行了分析。通过对节理岩质边坡的UDEC模型中的可变形块体和节理单元的强度参数进行折减，使模型不能再达到平衡状态，此时的折减系数就是边坡的安全系数，另外，由对应的边坡块体的速度矢量可以确定滑动面和边坡的破坏形态。郑惠峰等[5]将块体单元法与极限分析上限法相结合提出了岩石边坡稳定的块体单元极限分析上限法，借助于块体单元法离散计算区域，通过块体系统速度场在结构面上满足Mohr－Coulomb屈服条件、关联流动法则、速度边界条件以及块体系统虚功原理，构成求解边坡强度储备安全系数上限解的非线性规划模型，模型的求解采用复合形法。刘立鹏等[6]基于非线性强度准则——Hoek－Brown强度准则，利用slide软件，选取地质力学指标GSI、岩石力学参数mi、应力扰动系数D、边坡高度H及坡角β作为影响边坡稳定性的主要因素进行分析。王林峰等[7]以反倾岩质边坡为研究对象，根据岩块结构面的受力模式，构建了岩块结构面的断裂力学模型，并基于断裂力学建立了各岩块结构面等效应力强度因子的求解方法和稳定性判据。

早期的岩质边坡稳定性分析采用材料力学和简单的匀质弹性、弹塑性理论为基础的半经验半理论性质的研究方法，由于其力学机制的粗浅和假设的不合理，其计算结果与实际情况往往差距较大。由于岩质边坡坡体岩体的不连续性，本文采用了目前应用比较广泛的离散元法对某露天开采矿场的岩质边坡实例进行了稳定性分析。

1 工程概况

该露天开采矿坑边坡的坡角整体介于40°～45°之间，长约550m、宽约500m、高约270m的固定高陡边坡，坡底高程1 180.0m，坡顶高程1 460.0m（如图1所示）。研究区岩性单一（如图2所示），主要由基性深层侵入岩石辉长岩组成，岩体较破碎，节理发育。通过对研究区域坡体的结构面进行DIPS软件统计分析，得出该边坡的2组主要优势节理，其产状：233°∠59°、60°∠80°（如图3所示）。边坡坡脚位置可见岩石裂隙水渗出，边坡地质构造较复杂，贯穿于边坡的软弱结构面有断层、泥化夹层等。根据设计采场最终露天底为1 030.0m，该矿坑边坡最终将形成高达430.0m的人工边坡。因此为了工程边坡开挖安全，有必要对其开挖后斜坡体稳定性进行评价。

图1 矿坑边坡全貌

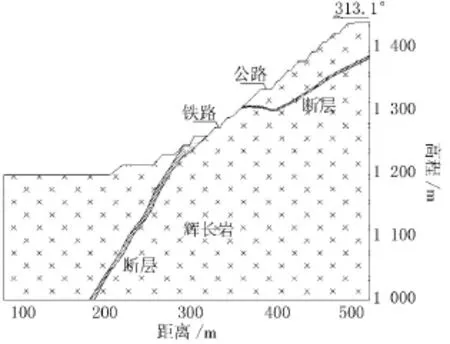
图2 工程地质剖面图

图3 结构面统计云图

2 模型的建立

由于不同类型的结构面及其空间的分布状况将决定岩质边坡的破坏模式，因此必须对边坡岩性、结构面以及物理力学参数进行详细的调查研究。在此基础上，结合现场调查结果，选取典型的地质剖面图，建立二维离散元模型（如图4所示）。

该二维离散元模型选取了2组优势节理，其产状：233°∠59°、60°∠80°，由于考虑边坡表面卸荷回弹以及风化的影响，深部岩体的完整性比浅表层的岩体完整性好，所以接近坡表的那一部分岩体节理间距为5m，坡体深处的岩体节理间距为15m，浅表层的岩体块体划分比深部岩体块体划分密集。坡体内贯穿2条断层，断层带内的节理为随机节理，断层带内节理形成的块体更为密集；考虑地下水渗流的影响，模型左边界水位高度为开挖底线至底边界距离的30m，右边界的水位高度为384m，初始应力为自重应力场。由于岩体的破坏主要受结构面的控制，假定岩体的破坏只沿着结构产生，因此岩体中的岩石块体选择各向同性的弹性模型，岩体中的结构面选择广为使用的莫尔－库伦模型；模型左右两侧边界约束水平x方向的位移，底部边界约束竖直y方向的位移，开挖面为自由面；计算工况为边坡开挖工况，未开挖前坡底高程为1 195m，开挖后坡底高程为1 150m，开挖深度45m。

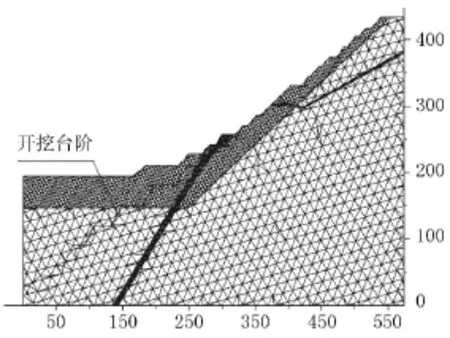
图4 二维离散元计算模型

根据岩石常规三轴试验，换算求得岩石块体和结构面的力学参数（见表1）。

3 数值模拟结果分析

3.1 天然状态下应力状态及变形特征

边坡在天然状态下，只在自重应力场的作用下达到平衡状态时，二维离散元数值模拟结果如图5所示。

表1 岩石块体和结构面的力学参数

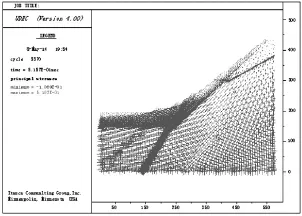
图5 天然状态下的主应力矢量

从主应力矢量图5可知，斜坡体在天然状态下的最大主应力和最小主应力分布符合一般斜坡体主应力分布特征，即总体上从上到下最大主应力和最小主应力逐渐增大，且离地表越深处最大主应力方向为竖直方向，最小主应力为水平方向。在靠近坡面附近，最大主应力和最小主应力的方向发生明显的偏转，主要表现为越靠近坡表处最大主应力与坡面平行，最小主应力与坡面垂直。同时，在越靠近坡表处，最小主应力由开始的压应力转化为拉应力，这说明斜坡体在形成斜坡的过程中斜坡表面处的岩体发生了卸荷回弹。此外由于断层带内的块体划分比其他地方多，故主应力矢量也相应密集。

图6 天然状态下位移矢量图

从斜坡体位移矢量图6可知，斜坡体在天然状态下，最大位移为4.377mm，这说明斜坡体在天然状态下是稳定的，且最大位移发生在坡脚处方向指向临空面，这说明斜坡体的最大位移主要是由于卸荷回弹引起的。

3.2 边坡开挖后的应力状态及变形特征

从图7可知，斜坡体在开挖后斜坡体内的主应力分布规律仍然符合一般斜坡体的主应力分布规律，即最大主应力和最小主应力随着深度的增加而增大，且距地表越深处最大主应力方向为竖直方向，最小主应力方向为水平方向，靠近坡表处最大主应力与最小主应力的方向发生明显偏转，越靠近坡表处，最大主应力与坡面平行，最小主应力与坡表垂直，且靠近坡表处的最小主应力由压应力转化为了拉应力。但是图7与图5比较，我们可以知道，开挖前与开挖后斜坡体最大压应力与斜坡体表面处的拉应力的数值发生了明显的变化，开挖前斜坡体的最大压应力为－10.69MPa，最大拉应力为0.510 2 MPa，拉应力主要是由于卸荷回弹引起的，开挖后斜坡的最大压应力为－35.5MPa，且集中在坡脚处，是开挖前最大压应力的3倍，开挖后坡脚处的压应力集中比开挖前更为明显，开挖后斜坡体的拉应力为2.168MPa，是开挖前斜坡最大拉应力的4倍，这说明开挖后的最大拉应力主要是由于斜坡体开挖扰动引起斜坡体表面处的岩体下滑而引起的。

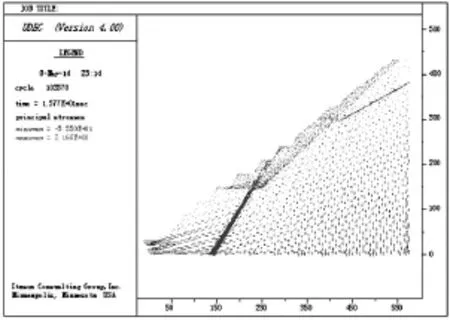
图7 开挖后的主应力矢量

图8 开挖后的位移矢量图

从图8可知开挖后，斜坡体最大位移为1.438m，发生在斜坡的中上部浅表层岩体，这也正是拉应力比较集中的地方，这也说明由于开挖扰动，斜坡体中上部的局部岩块沿着结构面发生了滑动掉块现象，但是斜坡体并没有由于开挖发生整体失稳的现象。从结果当中可以看出斜坡体内的两条断层带并没有对斜坡的稳定性造成多少影响，这主要是由于上部的断层带几乎是接近水平切入斜坡体的，斜坡浅表层的岩体很难沿着此软弱带滑出，虽然断层在斜坡体深部处发生偏转，倾角变陡，但是距离坡表较远，对坡表处的岩体稳定性影响甚微。另一条断层带虽然倾向坡外，但是由于倾角大于斜坡体的坡角，断层不能从坡面切出，岩体也不能沿此软弱带滑动。