基于二维参数辨识的蓄电池SOC估计

张金龙，漆汉宏

(燕山大学电气工程学院，河北秦皇岛066004)

基于二维参数辨识的蓄电池SOC估计

张金龙，漆汉宏

(燕山大学电气工程学院，河北秦皇岛066004)

针对铅酸蓄电池在工程应用中其荷电状态(SOC)难以准确估计的问题，本文结合常见的等效电池模型，采用等效电动势法对蓄电池SOC进行了实时估计。与普遍应用的恒参数的电池模型不同，本文通过统计辨识的手段，在不同SOC状态下以及不同的放电倍率条件下对等效模型进行了二维参数辨识。辨识结果表明，电池模型参数在不同的SOC状态下以及不同的放电倍率条件下均存在着较大差别;采用这种二维参数辨识方法估计出的电池SOC能够更加准确地跟踪电池的实际SOC。试验测试验证了这一SOC估计策略的准确性和实用性。

铅酸电池;荷电状态;放电倍率;等效模型;二维参数辨识

1 引言

电动汽车(EV)已成为当前的研究热点之一，在EV技术体系中，动力电池及其管理系统(BMS)是一项关键技术，而电池荷电状态(SOC)的估算更是BMS中的难点［1-3］。本文以准确估计电池SOC为研究目的展开。

针对阀控铅酸(VRLA)电池，本文选用常用的Thevenin蓄电池模型［4，5］对电池的SOC进行估计。研究表明，电动势法存在的最大问题是模型误差，为了能够更准确地跟踪电池实际工作特性，本文引入了一种二维参数辨识策略，对处于不同SOC状态下以及不同放电倍率下的电池模型参数进行统计分析。这样在SOC实际估算过程中，就可以实时根据电池SOC和放电倍率这两个状态对模型参数进行动态选取，从而达到准确估算SOC的目的。

2 电池模型的建立

出于工程实现方便和参数辨识容易执行方面的考虑，本文选取了目前广泛使用的Thevenin模型［6-8］，如图1所示。它主要由等效电动势E、欧姆电阻R1、极化电阻R2和极化电容C组成。

根据模型中的电气关系可知:

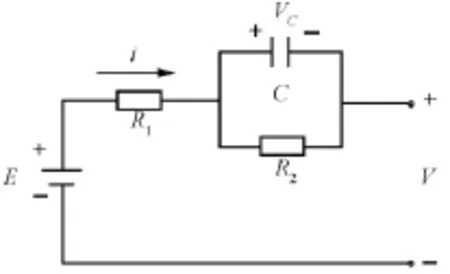
图1 Thevenin模型Fig.1Thevenin model

零初始条件下其拉氏变换为:

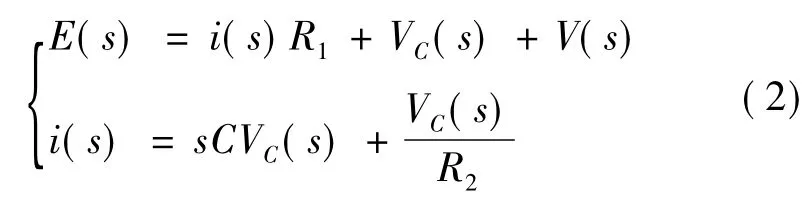
整理后消去VC(s)可以得到:

令θ=(R1+R2)/(R1R2C)，对式(3)进行Z变换可得:

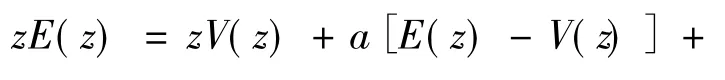
式中

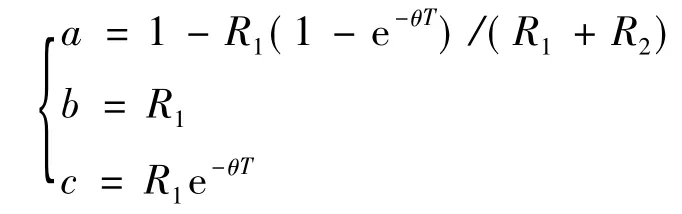
其中，T为采样周期。因此可以得到:

式中，V(k)、V(k－1)、i(k)和i(k－1)均为可直接测量的量，只需给出初始值E(0)并辨识出a、b、c三个系数的值即可得到E(k)。电动势E与电池SOC存在着对应关系，得到电动势E即可获得对应的SOC。

3 基于二维参数辨识的电动势法

3.1 SOC估算的整体流程

本文所实现的基于二维参数辨识的SOC估算整体流程如图2所示。

图2 SOC估算的整体流程Fig.2Flowchart of SOC estimation

进行SOC估算时，先根据当前放电倍率及上一周期SOC这两维状态进行查表，从而确定算法系数a、b和c的取值;接着就可以结合差分方程式(5)对当前电动势E进行估计;最后根据估计出的电动势E结合E-SOC对照表来确定电池当前SOC。在整个过程中二维系数表和E-SOC对照表是关键环节，二者都是根据测试数据采用统计辨识和曲线拟合的方法获得的。

E-SOC对照表的提取如图3所示，其方法是先采用标准电流(0.1C)对电池进行等电量间歇充电测试，每个充电阶段充入电量约为ΔSOC=10%，且每个充电段后都有1h的静置期，取充电过程各静置期电压的极值即可得充电E-SOC曲线;再采用相同的方法进行放电测试，可获得放电E-SOC曲线;最后取充放电E-SOC曲线的平均值作为最终的ESOC关系，该方法在文献［9］中有详述。

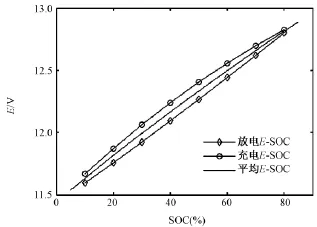
图3 E-SOC关系曲线的提取Fig.3Extraction of E-SOC relationship

3.2 二维系数表的辨识

要辨识出期望的二维系数表，首先要进行一系列放电测试，所测试蓄电池为INT系列6FM40型12V/40A·h VRLA蓄电池，共选用三组性能基本一致的单体。测试方法是采用不同的放电倍率分别对充满电的VRLA电池进行恒流间歇放电，直到电池电压达到最低门限电压为止。所谓间歇就是在每两个放电阶段之间加入一个时长为1h的静置时间。测试原则如下:

(1)充满状态。采用三段式12V VRLA电池充电器对蓄电池进行持续充电，充电达到10h后，视作电池充满。

(2)放电截止条件。任意倍率条件下电池端电压降到截止电压10V，停止放电。

(3)放电标准。不管采用哪种倍率，保证每个放电段放出的电量均为4A·h(最后一个放电阶段除外)，即每个放电段对应电池SOC的变化量基本相等。

(4)分别采用0.05C、0.1C、0.15C、0.2C和0.25C五种倍率对电池进行放电。

如图4所示，模型将静置时段等效为欧姆电阻掉电和极化电容放电的过程，在此首先研究极化电容放电过程，根据式(1)，当放电结束时放电电流为零，故有:

若取放电停止时刻为t=0，则在静置段采用曲线拟合，选用的函数形式可写为:

式中，α=E(0)，为电池在静置段内的实际电动势，静置时为恒定值;β=iR2，为电容放电前的初始电压值，也即放电过程中电阻R2上产生的压降;λ =1/(R2C)，为时间常数τ的倒数。

图4 基于模型函数拟合的参数统计辨识法Fig.4Parameter identification based on curve fitting

根据此辨识方法可以得到α、β和λ三个量，于是可以首先通过放电电流i确定极化电阻R2;接着便可以得到极化电容C;最后根据电压的瞬时突变来确定欧姆电阻R1，电压瞬时突变量可以由总的电压变化量减去电容C的初始电压得到。按照这种方法，便可以得到不同的放电倍率下，以及不同的电池SOC状态下电池模型各参数对应的数值，辨识结果如图5所示。

根据参数辨识的结果可以发现:在电池的工作平台区(30%≤SOC≤90%)内，模型中的等效电阻R1和R2都随着放电倍率的提高有一个明显减小的趋势，而在固定的放电倍率下，两者的数值则相对比较稳定;整体来看R1和R2又随着SOC的降低有着明显的增大趋势;极化电容C随电池SOC的降低总体上有一个增大的趋势，当采用不同倍率放电时，对于处于平台区的VRLA电池而言，在相同的SOC状态下其等效电容之间的差异并不大。

虽然在工作平台区内模型参数较稳定，但当电池工作于平台区以外时，特别是当SOC低于30%时，电池会工作于一种高度非线性的状态，参数变化非常迅速，本文重点研究平台区内特性。

接着就是根据得出的一系列电阻电容参数，结合式(3)～式(5)进一步确定电动势算法中的系数a、b和c的数值，这三个参数将直接参与电池电动势的实时递推。最终可以得到如表1所示的二维系数表。

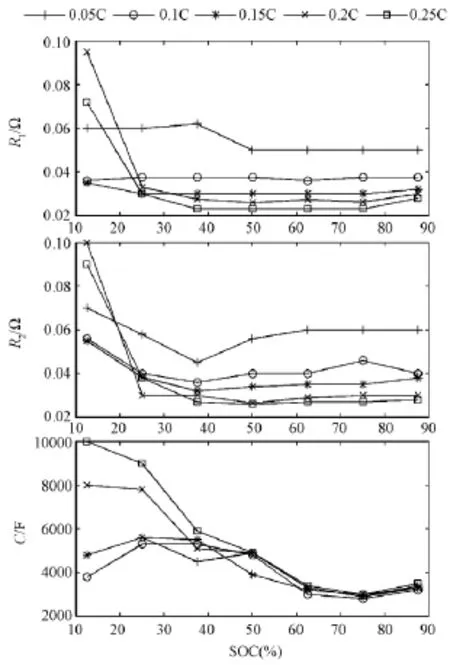
图5 三个模型参数的辨识结果Fig.5Identification result of three model parameters

表1 二维系数表Tab.1Two-dimensional coefficient table

得到二维系数表后，就能在电动势的递推过程中根据当前放电倍率和当前SOC状态进行查表，从而确定算法系数。

4 实验分析

实验平台总体结构如图6所示。电池仍采用INT系列6FM40型VRLA蓄电池，额定容量40A·h，实际可用容量约32A·h;充放电采用三段式充电器和DSS1K8E智能放电仪;BMS平台则采用自行开发的基于TI DSP2407的信号检测和处理系统以及基于VC++的上位机监控平台。

图6 BMS结构图Fig.6BMS structure

采用上文提出的SOC估计策略结合BMS平台对处于放电状态的电池进行了实时SOC估计，试验结果如图7和图8所示。

图7为采用标准电流4A给蓄电池持续放电时，分别采用恒定参数模型和二维参数辨识策略对电池SOC进行实时估计的结果。可见采用恒定参数电池模型得到SOC曲线产生了明显的误差，在电池工作状态切换时产生的误差尤为明显。而采用二维参数辨识后所估算出的SOC则能够比较准确地跟踪理想SOC曲线。

接着又进行了随机电流间歇放电测试，SOC估计结果如图8所示。可见采用恒定参数电池模型估计出的SOC曲线虽然在起始阶段还比较准确，但在放电中期2A小倍率放电阶段却产生了较大的误差。相对而言，采用二维参数辨识策略对电池SOC进行估计时，虽然在状态切换时仍存在一定误差，但总体而言所产生的误差有明显减小。由此可见，采用这种带有动态参数的等效模型可以更加准确地实现蓄电池的SOC的估算。

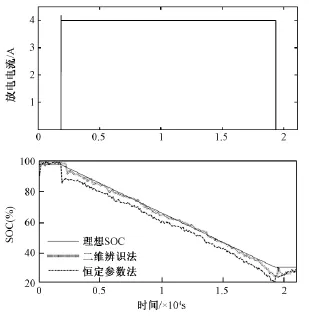
图7 恒流放电SOC估计结果Fig.7Estimated SOC results of constant current discharge process

图8 随机电流放电SOC估计结果Fig.8Estimated SOC results of random current discharge process

5 结论

本文首先结合Thevenin等效模型，提出了一种二维参数辨识策略，提高了电池模型的精度;接着详细介绍了参数辨识步骤，二维系数表的建立流程以及应用方法;最后基于TI DSP2407搭建了实验平台，并对处于工作状态的VRLA蓄电池进行了实时SOC估计。实验结果表明，采用二维参数辨识策略建立的动态参数电池模型能够更加准确地反映蓄电池的实际工作性能，通过这种方法估计出的电池SOC也更加准确，整个策略具有很强的实用性。

［1］李红林，张承宁，孙逢春，等(Li Honglin，Zhang Chengning，Sun Fengchun，et al.).锂离子电池组均衡充电和保护系统研究(Research on equal charging and protection system of Li-ion battery pack)［J］.北京理工大学学报(Transactions of Beijing Institute of Technology)，2004，24(3):210-211.

［2］李书旗，沈金荣(Li Shuqi，Shen Jinrong).蓄电池组均衡电路的设计与实验(Design and experiment of balancing circuit for rechargeable battery pack)［J］.科学技术与工程(Science Technology and Engineering)，2009，9(13):3081-3085.

［3］刘洁，王菊香，邢志娜，等(Liu Jie，Wang Juxiang，Xing Zhina，et al.).燃料电池研究进展及发展探析(The Investigation on research progress and development of fuel cell)［J］.节能技术(Energy Conservation Technology)，2010，28(4):364-368.

［4］Sabine Piller，Marion Perrin，Andreas Jossen.Method for state-of-charge determination and their applications［J］.Journal of Power Sources，2001，96(1):113-120.

［5］夏超英，张术，孙宏涛(Xia Chaoying，Zhang Shu，Sun Hongtao).基于推广卡尔曼滤波算法的SOC估算策略(SOC estimation strategy based on extended Kalman filter algorithm)［J］.电源技术(Power Source Technology)，2007，31(5):414-417.

［6］Mao Chunsheng，Zhong Shaohua，Hu Yunda.SOC estimation of EV battery based on improved Thevenin model［J］.Technology of Power Supply，2005，382(18): 106.

［7］M Sarvi，M A S Masoum.A neural network model for Ni-Cd batteries［A］.43rd International Universities Power Engineering Conference，UPEC 2008［C］.2008.1-5.

［8］Jrn A Tinnemeyer.Multiple model impedance spectroscopy techniques for testing electrochemical systems［J］.Journal of Power Sources，2004，136(2):246-249.

［9］Zhang Jinlong，Xia Chaoying.Application of statistical parameter identification strategy in BMS［A］.Proceedings of the 8th WCICA［C］.2010.5938-5942.

Battery SOC estimation based on two-dimensional parameter identification

ZHANG Jin-long，QI Han-hong
(School of Electrical Engineering，Yanshan University，Qinhuangdao 066004，China)

In order to correctly estimate the state of charge(SOC)of valve regulated lead-acid battery under actual engineering applications，an improved SOC estimation method based on a commonly used equivalent battery model is presented.Unlike the battery model with constant parameters，a two-dimensional parameter identification strategy is employed，and model parameters are identified under different SOC state and different discharge rates.Identification results show that there are noticeable differences among parameter values under different conditions.After adopting this two-dimensional parameter identification strategy，the estimated SOC can track the ideal SOC curve more correctly;the subsequent experimental results of this SOC estimation method are satisfactory，accurate and practical.

lead-acid battery;state of charge(SOC);discharge rate;equivalent model;two-dimensional parameter identification

TM911;TM912

A

1003-3076(2014)09-0030-05

2013-04-02

张金龙(1983-)，男，河北籍，讲师，博士，研究方向为电池管理系统、数字信号处理;漆汉宏(1968-)，男，江西籍，教授，博士生导师，研究方向为新能源发电及并网技术。