直驱式波浪发电系统浮子形状与排布优化研究

肖曦，摆念宗，康庆

(1.清华大学电机系电力系统及发电设备控制和仿真国家重点实验室，北京100084; 2.中国空间技术研究院通信卫星事业部，北京100094)

直驱式波浪发电系统浮子形状与排布优化研究

肖曦1，摆念宗1，康庆2

(1.清华大学电机系电力系统及发电设备控制和仿真国家重点实验室，北京100084; 2.中国空间技术研究院通信卫星事业部，北京100094)

提出通过浮子形状和排布结构的优化，提高直驱式波浪发电系统(DDWEC)的能量吸收效率，并改善输出功率波动问题。文中推导分析了DDWEC水动力模型，提出了水动力参数的优化原则，根据优化原则提出了浮子形状的优化措施，采用WAMIT软件仿真验证了对提高能量吸收效率的有效性;同时，基于浮子优化结果，在考虑浮子间互相影响的情况下，通过波浪发电场的排布结构优化，改善了DDWEC功率波动的问题，削弱了遮蔽效应等浮子间的影响，提高了波浪发电场的能量吸收效率。

直驱式波浪发电;功率波动;浮子形状;排布结构;优化

1 引言

波浪能作为一种清洁无污染的可再生能源，具有很好的开发前景。相比于其他可再生能源(如风能和太阳能)，波浪能具有能量密度高、可预测性好等优点［1，2］。全球波浪资源储量丰富，但分布差异较大［3］，中国波浪能主要集中在东南沿海以及一些海岛地区，具有很好的开发应用潜力，但目前相关领域基础研究缺乏，限制了波浪能的实际应用［4］。

波浪的速度和频率较低，需要提速环节才能驱动传统电机，而这会增加系统的复杂性。直驱式波浪发电装置(Direct-Drive Wave Energy Converter，DDWEC)采用直线电机直接将波浪能转换为电能，由于没有提速环节，其所需的离岸维护最少，因此成本也大大降低，具有很高的可行性［5］。

直驱式波浪发电系统也面临着自身的一些问题。一方面，海面波况变化时，直驱式系统的输出功率也会波动，对电网的稳定性及电能质量都会产生不利影响;另一方面，即使波况恒定，由于直驱式系统自身的特性，其产生的功率幅值变化也非常大，甚至出现零功率时刻。这些特点使得系统输出的电能质量变差，增大了电力电子设备的容量，大大降低了其利用率。因此，如何平抑功率波动成为直驱式波浪发电系统的一个重要研究课题。

对于单个WEC来说，可以通过一些控制方法以及储能系统来实现功率波动的平抑［6，7］，然而单纯使用这些方法会使系统更加复杂同时成本也会增加。随着波浪发电规模的增大，可以通过优化发电场排布的方法平抑波动。比较简单的排布方式就是整体布局［8，9］，比如将发电场布置成圆形或方形;另外还有基于系泊装置约束的排布方式［10］;文献［11］也对浮子的相对位置进行了分析。但是以上研究都未对浮子间距等因素的影响进行深入分析，也很少考虑浮子间的相互作用(称之为“浮子效应”)。因此，本文从本质上分析了浮子间距对于平抑功率波动的效果，同时研究了排布的浮子效应，优化了波浪发电场的排布。

此外，波浪发电的转换效率普遍较低，一般为10%～30%［12］，而通过改善浮子形状，可以一定程度提高波浪能捕获效率。例如，经典的点头鸭装置［13］，Marine Power System Limited公司设计的环形浮子［14］，以及SEABASED公司设计的多边形浮子［15］等。本文通过对比几种常规形状的浮子，分析浮子形状的优化特点，进而提高单个WEC的能量吸收率。

2 水动力分析

2.1 水动力模型

浮子在水中受波浪作用，有六个自由度的运动。本文研究的直驱式WEC仅限定浮子做垂直方向的振荡运动，其在水中的受力如图1所示。

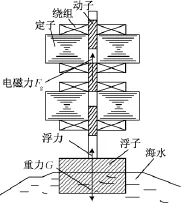
图1 直驱式WEC浮子受力图Fig.1Force diagram of DDWEC buoy

由图1可见，浮子主要受到波浪的浮力(包括波浪激励力、辐射力和静恢复力)、电磁力以及重力的作用。根据牛顿第二定律，其运动方程为:

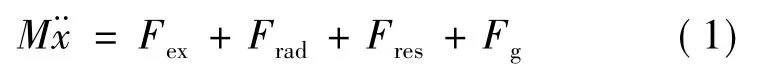
式中，M为包含浮子和发电机动子等运动部件的总质量;Fex为波浪激励力;Frad为辐射力;Fres为静恢复力;Fg为发电机电磁力。

在规则波中，辐射力Frad为［16］:

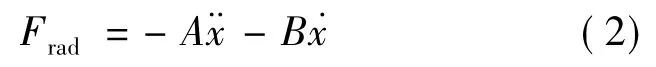
式中，A为附加质量;B为附加阻尼。静恢复力Fres为:

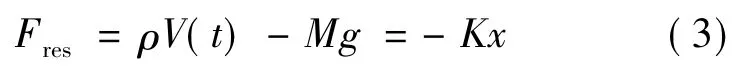
式中，V(t)为浮子的吃水体积;ρ为海水密度;g为重力加速度;K为静恢复力系数，可以表示为K= ρgSw，其中Sw为浮子水线面积。

系统线性化，发电机反电磁力Fg可写为:

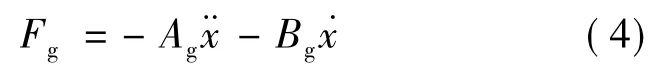
式中，Ag为电磁力等效惯性系数;Bg为电磁力等效阻尼系数。

因此，式(1)可以写为:

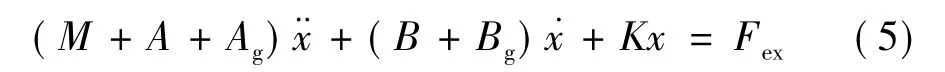
可以将式(5)等效为RLC电路，如图2所示。

2.2 功率捕获

为了让WEC能够捕获更大的功率，可以通过控制电磁力等效系数，使系统频率与波浪频率相匹配，即:

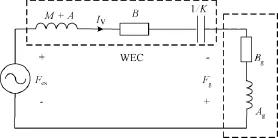
图2 RLC等效电路Fig.2RLC equivalent circuit

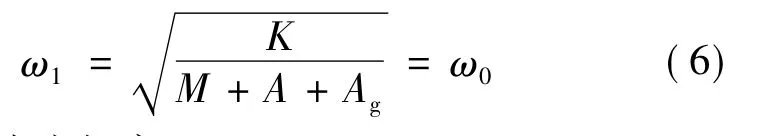
式中，ω0为波浪频率，ω0=2π/T。

实际上，这种状况很难实现。当电磁力等效系数达到匹配条件时，浮子的速度将会非常大，超出系统的速度及冲程限制，甚至会损坏装置。因此，实际WEC的优化控制是在考虑系统各类约束的情况下，使系统尽量接近频率匹配状态。

浮子运动幅值为:

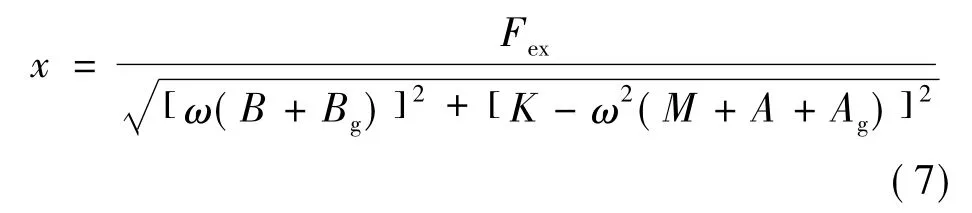
WEC吸收的平均功率为:

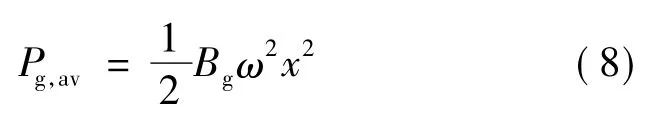
WEC的吸收宽度可以定义为单位波峰长度吸收功率与可用功率的比值［2］，即:

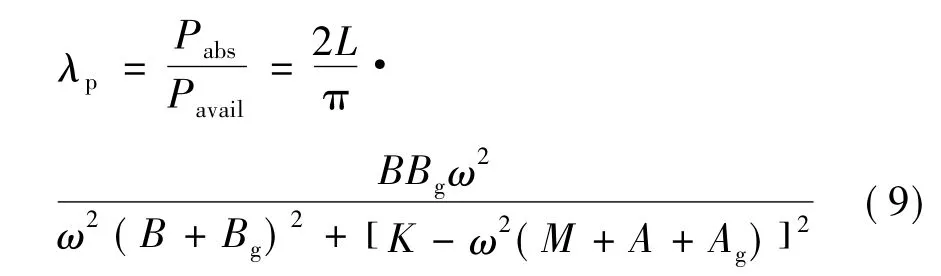
式中，L为波长;λp最大值称为最大吸收宽度。

对于直径为D的浮子，波浪发电装置的能量吸收效率为:

浮子的形状会影响水动力系数，进而表现为影响能量的吸收。因此，需要研究什么样的水动力系数会使系统的吸收效率更高。

一般K＞ω2(M+A+Ag)，由式(9)可以看出，为了使吸收宽度λp更大，附加质量A和运动部件质量M需要增大。对于附加阻尼B，当满足式(11)时，吸收宽度最大。通常B＜Bmax，所以在优化浮子形状时，应使B尽量大一些。

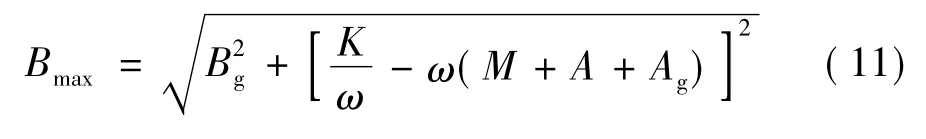
3 浮子形状优化

浮子是WEC的能量捕获单元，因此浮子形状的好坏，直接影响着波浪发电装置的能量捕获效率。本文比较了不同浮子形状、不同吃水深度以及不同浮子半径情况下的能量吸收效果，从而得到浮子优化的基本原则。

3.1 浮子形状

本文对比了六种浮子形状，分别为四棱柱、四棱锥、圆柱、半球、圆台以及圆锥，如图3所示。选取浮子半径R=3m，吃水深度Dt=3m，采用流体动力学分析软件WAMIT计算其水动力系数以及激励力等参数，并进一步计算其输出功率以及吸收效率。水动力系数与激励力的计算结果如图4～图6所示。

从图4～图6可以看出，对于同一浮子，当波浪周期不同时水动力系数和激励力也不同，随着波浪周期的增大，附加质量逐渐增大并趋于恒定，附加阻尼逐渐趋于零，波浪激励力也逐渐增大并趋于一个恒定值。

对比不同类型浮子可以看出，圆形浮子(圆柱、半球、圆台、圆锥)的水动力系数和激励力整体要比方形浮子(四棱柱、四棱锥)大，因此更加适合吸收能量;而对比同类型浮子，方形浮子的水动力系数大小为:四棱锥＞四棱柱，圆形浮子的水动力系数大小为:圆锥＞圆台＞半球＞圆柱，对于激励力也有同样的规律，因而可以发现:“上大下小”型的浮子水动力系数和激励力更大，更易吸收能量。

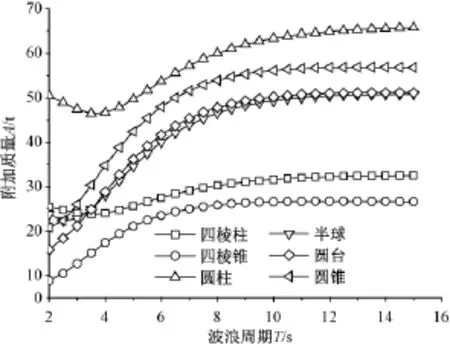
图4 不同波浪周期浮子的附加质量Fig.4Added mass coefficients for different wave periods

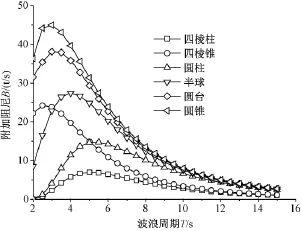
图5 不同波浪周期浮子的附加阻尼Fig.5Added damping coefficients for different wave periods

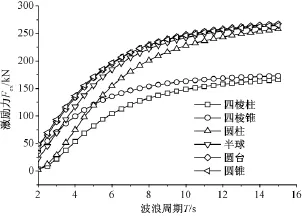
图6 不同波浪周期浮子的激励力Fig.6Exciting forces for different wave periods

为验证上述不同形状浮子的能量吸收效果，本文进一步对比了吸收功率以及吸收效率。由式(8)～式(10)可以看出，WEC的吸收功率和效率不仅和浮子本身的特性有关，还和电磁力等效系数Ag、Bg相关。同时，实际WEC装置也有速度和冲程等限制，如AWS系统额定速度为2.2m/s［17］。因此，本文选取中国沿海常见波况:波浪周期T=6s、波高Hw=2m，优化电磁力等效系数使浮子运动幅值为2m，然后比较浮子的功率捕获效果，如图7和图8所示。

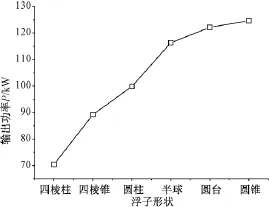
图7 不同形状浮子的输出功率Fig.7Power outputs for different buoy shapes

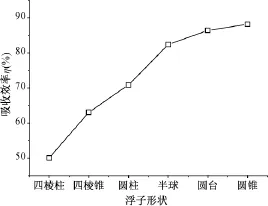
图8 不同形状浮子的吸收效率Fig.8Absorption efficiencies for different buoy shapes

可以明显看出，能量吸收效率和前面水动力系数优化趋势是一致的，从而也验证了通过优化浮子形状，可以提高WEC的能量吸收率。但是，能量吸收效果越好，相应付出的代价也越大。图9所示为不同浮子的电磁力等效系数，很显然，能量吸收效率越高，对应的电磁力等效系数越大，因而对系统的要求也更高。

3.2 吃水深度

为了研究吃水深度对浮子能量吸收的影响，本文对比了半径R=3m的圆锥形浮子不同吃水深度的能量吸收效果，同样使用上述条件，结果如表1所示。

从表1数据可以看出，随着吃水深度增大，WEC的能量吸收率相应减小，然而由于圆锥体吃水深度变化引起的吃水体积变化不大，因此其差异也不是很大。但是依然可以看出，吃水深度越小，相应的水动力系数越大，吸收效果也越好。过小的吃水深度会导致浮子运动时容易冲出水面，这显然不利于系统稳定性。因此，通过减小吃水深度改善吸收效果的同时，还要保证浮子不容易脱离水面。

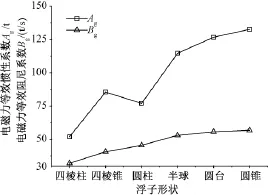
图9 不同形状浮子的电磁力等效系数Fig.9Electromagnetic equivalent coefficients for different buoy shapes

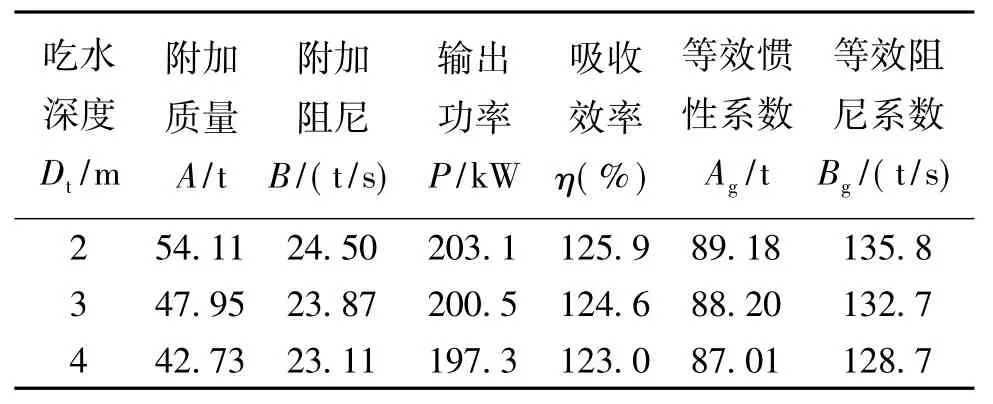
表1 不同吃水深度，能量吸收效果Tab.1Energy absorption effects for different drafts

3.3 浮子半径

对于某一海况，选择多大半径的浮子，波浪能的吸收效果最好，空间利用率最高，这也需要进行研究。同样对于前述给定条件，比较不同浮子半径的能量吸收效率，结果如表2所示。

表2 不同半径，浮子能量吸收率Tab.2Energy absorption efficiencies for different radii

由表2可以看出，浮子半径越大，其能量吸收率也越大。但是在实际选择中，并不是浮子越大越好，一方面浮子直径要小于式(9)的最大吸收宽度，和实际波况相匹配;另一方面还要根据应用场合设计合适的浮子大小，同时也要考虑成本因素。

4 排布结构

通过优化波浪发电场的排布结构，可以很大程度上平抑输出功率的波动。本节研究了排布结构的优化方法以及浮子效应，以改善波浪发电场的输出电能质量，同时提高能量吸收效率。

图10所示为一个波浪发电场的排布结构，整个波浪发电场可以看做是由虚线框所示的排布列单元组合而成。通过设定每个列单元的浮子数以及不同的列单元数，可以组合为任意形状的排布结构，比如圆形、方形等。因此，可以通过研究排布列单元的排布方式，来研究整个波浪发电场的排布结构优化。

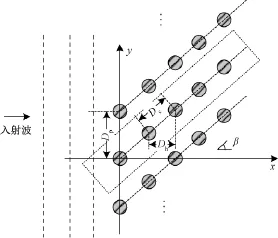
图10 波浪发电场排布Fig.10Array of wave power farm

4.1 功率波动平抑

单个WEC输出功率会出现波动，甚至在一个波浪周期内出现两次零功率。通过浮子的位置差，可以使不同浮子的峰谷功率互补，从而平抑功率波动。图11(a)所示为浮子的间距排布与某一时刻浮子位移的关系图，x轴为波浪传播方向，z轴为浮子运动方向。设定其顺波向间距Dh为λ/4，因此相邻浮子相位相差90°，输出功率正好峰谷互补。如图11(b)所示，虚线分别为相邻两个单浮子的功率，实线为相邻两浮子的合成功率，相比于单浮子输出功率，其波动大大减少，平抑效果非常显著。按照此相位差原理，浮子间距也可以设置成其他值，只要能够使浮子实现功率错峰，就可以达到波动平抑的效果。但是当Dh为λ/2的倍数时，各浮子功率会峰峰相加，导致功率波动更大，因此排布时应当避免这种情况的发生。

实际海洋的波浪周期不会一成不变，而波浪发电场在建成后其排布结构一般是固定的。因此排布结构要能适应不同的波浪周期。图12所示为排布结构固定(针对波浪周期T=6s设计)、当波浪周期变为7s时某一时刻各浮子的位移。可以看出，周期为6s时浮子间距为λ/4，对应周期7s时其间距约为λ/5，利用相位差原理可以知道，其功率波动平抑效果依然很显著。对于小于6s的某个波浪周期，该排布可能会出现峰峰叠加的情况。因此，针对某一实际海域进行排布结构设计时，需要考虑该海域不同的波况，选择合理的间距来避免峰峰叠加这一情况发生。

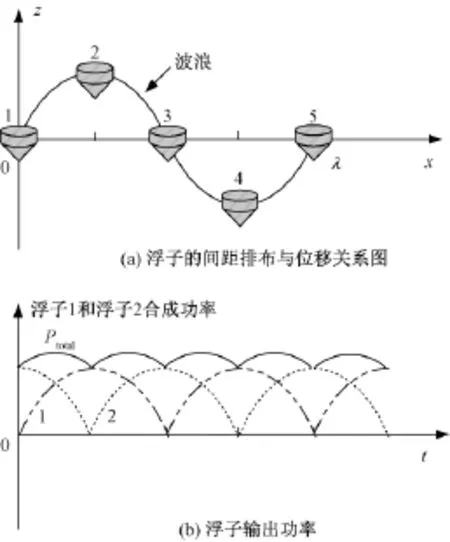
图11 浮子位置及合成功率Fig.11Buoy locations and aggregated power

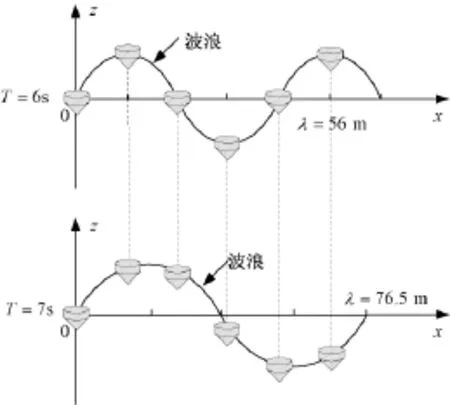
图12 排布间距适应不同波长Fig.12Array distance applied to different wavelengths

4.2 浮子效应

在设计排布结构时，不仅要考虑功率平抑，还应尽量减少遮蔽效应等浮子之间的影响，从而使整个发电场的能量吸收效率更高。因此，本文利用WAMIT研究了排布角以及排布间距对浮子效应的影响。列单元浮子均采用前述吸收效率较高的圆锥型浮子，半径R=3m，吃水深度Dt=3m;波浪采用周期6s、波高2m的常见波况。

4.2.1 排布间距

一般而言，间距越大，浮子效应越小。图13所示为β=0°时，不同间距列单元各浮子的激励力幅值。整体而言，间距越大，后方浮子所受遮蔽效应越小，因而激励力也越大。但是间距Dc=10m时激励力变化较大，一方面是由于间距过小导致遮蔽效应过大，后方浮子激励力变小，另一方面可能是由于后方浮子的反射波和入射波正向叠加，增大了前方浮子的激励力。

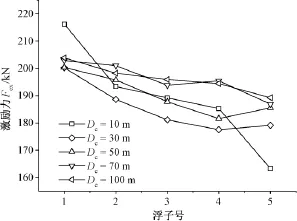
图13 不同排布间距浮子激励力，β=0°Fig.13Exciting forces for different array distances，β=0°

4.2.2 排布角

通过增大间距减弱遮蔽效应，其效果不是很显著，同时实际的波浪发电场要考虑空间利用率以及电力传输成本等因素，浮子间距也不能过大。因此，可以通过增大排布角β的方式，进一步减弱遮蔽效应。

图14所示为Dc=10m时，不同排布角列单元各浮子所受的激励力大小。明显可以看出，随着排布角的增大，后方浮子所受的遮蔽效应减弱，激励力随之增大。由于波浪发电场是由一个个列单元组成，因此过大的排布角同样会降低空间利用率，增加系统建设成本，所以一般选择一个适中的角度，比如45°。

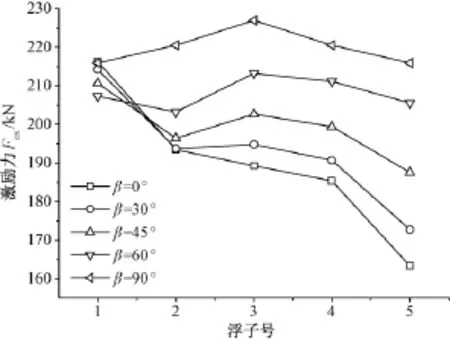
图14 不同排布角浮子激励力，Dc=10mFig.14Exciting forces for different array angles，Dc=10m

实际波浪不会一直从一个方向传播过来，波浪传播方向变化时，会增大或减小排布角。因此在建设波浪发电场时，要深入调研该区域的波浪状况。一般靠岸型波浪发电场，其波浪传播方向垂直于海岸线，因此比较容易处理;对于离岸型波浪发电场，其入射波方向可能会由于季风等因素的影响发生变化，但会有几个主要的传播方向，因此可针对这几个入射波方向进行优化设计。

5 结论

本文研究了直驱式波浪发电系统的浮子形状以及排布结构优化，主要结论如下:

(1)通过浮子形状的优化改善了单个WEC的能量吸收效率，总结出“上大下小”型的浮子可以捕获更多的波浪能量，同时浮子半径以及吃水半径对能量捕获效率也有影响，具体大小要依据当地波况以及系统要求来确定。

(2)通过排布结构的优化削弱了遮蔽效应，提高了整个波浪发电场的能量吸收效率;同时通过排布优化，大大平抑了直驱式波浪发电系统的功率波动，改善了电能质量，从而可以减少储能系统的容量以及电力电子设备的功率等级，降低系统的成本。

［1］Falnes J.A review of wave-energy extraction［J］.Marine Structures，2007，20(4):185-201.

［2］Brekken T.Fundamentals of ocean wave energy conversion，modeling，and control［A］.IEEE International Symposium on Industrial Electronics(ISIE)［C］.Bari，Italy，2010.3921-3966.

［3］Cahill B，Lewis T.Wave energy resource characterization and the evaluation of potential wave farm sites［A］.OCEANS［C］.Hawaii，USA，2011.1-10.

［4］Wang S，Yuan P，Li D，et al.An overview of ocean renewable energy in China［J］.Renewable and Sustainable Energy Reviews，2011，15(1):91-111.

［5］Nie Z，Xiao X，Yi H，et al.Direct drive wave energy converters integrated with a composite energy storage system［A］.International Conference on Electrical Machines and Systems(ICEMS)［C］.Beijing，China，2011.1-5.

［6］Valério D，Beirao P，Mendes M J G，et al.Comparison of control strategies performance for a wave energy converter［A］.16th Mediterranean Conference on Control and Automation［C］.Ajaccio，France，2008.773-778.

［7］Nie Z，Xiao X，Kang Q，et al.SMES-battery energy stor-age system for conditioning outputs from direct drive linear wave energy converters［J］.IEEE Transactions on Applied Superconductivity，2013，23(3):5000705.

［8］Molinas M，Skjervheim O，Srby B，et al.Power smoothing by aggregation of wave energy converters for minimizing electrical energy storage requirements［A］.Proceedings of the 7th European Wave and Tidal Energy Conference［C］.Porto，Portuga，2007.3-8.

［9］Taghipour R，Moan T.Efficient frequency-domain analysis of dynamic response for the multi-body wave energy converter in multi-directional waves［A］.Proceedings of the 18th International Offshore and Polar Engineering Conference［C］.Vancouver，Canada，2008.

［10］Vicente P C，de O Falco A F，Gato L，et al.Dynamics of arrays of floating point-absorber wave energy converters with inter-body and bottom slack-mooring connections［J］.Applied Ocean Research，2009，31(4):267-281.

［11］Sjolte J，Tjensvoll G，Molinas M.All-electric wave energy converter connected in array with common DC-link for improved power quality［A］.3rd IEEE International Symposium on Power Electronics for Distributed Generation Systems(PEDG)［C］.Aalborg，Denmark，2012.431-436.

［12］游亚戈(You Yage).我国海洋能产业状况(Status of marine energy industry in China)［J］.高科技与产业化(High-Technology and Industrialization)，2008，(7): 38-4l.

［13］Stephen H Salter.Apparatus for use in the extraction of energy fromwavesonwater［P］.UnitedStates: US4134023(A)，1979-01-09.

［14］Marine Power System Limited.Wave powered generator［P］.Europe:WO2013068748(A3)，2013-10-17.

［15］Seabased A B.A wave power unit，a buoy，use of a wave power unit and a method for producing electric energy［P］.Europe:EP2134960(A1)，2009-12-23.

［16］Falnes J.Ocean waves and oscillating systems［M］.Cambridge:Cambridge University Press，2004.

［17］De Sousa Prado M G，Gardner F，Damen M，et al.Modelling and test results of the Archimedes wave swing［J］.Proceedings of the Institution of Mechanical Engineers，Part A:Journal of Power and Energy，2006，220(8): 855-868.

Research on optimizations of buoy shape and array geometry of direct-drive wave energy converters

XIAO Xi1，BAI Nian-zong1，KANG Qing2
(1.State Key Lab of Power Systems，Dept.of Electrical Engineering，Tsinghua University，Beijing 100084，China;2.Institution of Telecommunication Satellite，China Academy of Space Technology，Beijing 100094，China)

In this paper，the optimizations of buoy shape and array geometry are studied to improve the energy absorption efficiency of direct-drive wave energy converter(DDWEC)and to smooth the output power fluctuations.The hydrodynamic model of DDWEC is derived and analyzed，therefore，the optimization rules of hydrodynamic parameters are summarized.Based on the rules，the optimization measures of buoy shape are proposed，and then the hydrodynamic software WAMIT is used to simulate and verify the improvement of the energy absorption efficiency.Meanwhile，considering buoys interactions，the array geometry of wave farm is optimized to mitigate power fluctuations and weaken the buoys interactions(such as shadowing effect)，based on the optimization results of buoy shape.As a result，the energy absorption of wave farm is increased.

DDWEC;power fluctuation;buoy shape;array geometry;optimization

TM619

A

1003-3076(2014)09-0007-07

2014-03-12

国家自然科学基金资助项目(51177084)

肖曦(1973-)，男，湖南籍，副教授，博士，研究方向为交流电机控制、海浪发电与电力储能;摆念宗(1988-)，男，甘肃籍，硕士研究生，研究方向为电力电子与电力传动。