欠观测条件下的增量容积卡尔曼滤波
2014-06-07马丽丽赵甜甜陈金广
马丽丽,赵甜甜,陈金广,2
(1.西安工程大学计算机科学学院,西安710048;2.西安电子科技大学电子工程学院,西安710071)
欠观测条件下的增量容积卡尔曼滤波
马丽丽1,赵甜甜1,陈金广1,2
(1.西安工程大学计算机科学学院,西安710048;2.西安电子科技大学电子工程学院,西安710071)
在工程实践中,由于环境影响、量测设备不稳定等因素,非线性滤波系统中的量测方程可能会出现较大的系统误差,而标准的非线性滤波算法不能消除这类系统误差。针对该问题,假定过程噪声和量测噪声服从高斯分布,利用相邻量测时刻的量测值之差建立增量量测方程,采用3阶球面径向规则获得容积点及其权值。使用容积点对贝叶斯滤波过程中的积分进行数值近似,从而提出增量容积卡尔曼滤波算法。仿真实验结果表明,增量容积卡尔曼滤波算法滤波精度优于标准容积卡尔曼滤波算法与增量卡尔曼滤波算法,能够成功消除量测方程中的系统误差。
增量量测方程;增量容积卡尔曼滤波;欠观测条件;卡尔曼滤波;状态估计;深空探测
1 概述
滤波就是在对系统可观测信号进行量测的基础上,根据某种估计准则,对系统的状态进行估计的理论和方法。应用于线性随机系统的最优估计即是卡尔曼滤波,对于非线性随机系统,可以对非线性函数进行泰勒级数展开进行线性化近似,再利用卡尔曼滤波算法进行处理,这就是扩展卡尔曼滤波算法。这些方法广泛应用于信号处理、导航制导等领域,并获得了巨大的成功[1]。为了获得更精确的滤波性能,出现了不敏卡尔曼滤波[2]、求积分卡尔曼滤波[3]、中心差分卡尔曼滤波[4]、粒子滤波[5]、容积卡尔曼滤波(Cubature Kalman Filtering,CKF)[6]等方法,这些方法都能够有效地在一定程度上提高滤波的精度。其中,粒子滤波算法滤波精度最高,但是计算量很大。近年来出现的容积卡尔曼滤波算法计算量较小而且滤波精度较高,受到了研究人员的关注。文献[7]针对系统噪声为加性的情况,结合扩维的思想提出了扩维容积卡尔曼滤波,能够进一步提高滤波精度。文献[8]提出了均方根容积信息滤波器,能够提高容积卡尔曼滤波器的数值稳定性和计算效率。针对连续离散系统,文献[9]提出了连续离散容积卡尔曼滤波器,对标准容积卡尔曼滤波器进行了扩展,使其适用于动态方程为连续型而量测方程为离散型的情况。针对只测角跟踪系统,文献[10]将容积卡尔曼滤波器融入到高斯和滤波框架中,能够获得较好的滤波性能。
然而,在一些应用中,例如深空探测,由于环境因素的影响,量测设备的不稳定性、模型和参数的选取不当等因素,造成量测数据中的系统误差随时间变化而漂移。此时,标准的滤波算法不能够消除量测系统误差。为了解决该问题,针对线性系统,文献[11]提出了增量Kalman滤波算法,该算法能够成功消除未知的量测系统误差,大大提高了卡尔曼滤波的精度。针对非线性系统,提出了相应的扩展增量卡尔曼滤波[12]、无迹增量卡尔曼滤波[13]、增量粒子滤波等算法[14]。
为进一步提高增量滤波算法的精度,本文提出增量容积卡尔曼滤波算法,为增量滤波方法提供了新的实现途径。
2 问题描述
假定具有加性噪声的非线性系统如下:

其中,xk表示状态向量;zk表示观测向量;f和h分别表示非线性状态转移函数和量测函数;ak表示由于量测方程建模与实际量测模型之间存在的未知系统误差;wk-1和vk分别表示过程噪声和量测噪声,均值为0。通常假设噪声分量满足高斯分布,且:

若直接采用容积卡尔曼滤波算法进行滤波,则由于式中存在未知系统误差分量ak,使得滤波结果误差较大,甚至发散。为了解决该问题,令:

若采样足够密集,则ak-ak-1→0,可得:

增量量测方程中的随机噪声分量Vk=vk-vk-1,由于2个高斯分布的随机变量之和(差)仍然服从高斯分布,且均值为2个随机变量均值之和(差),协方差为:

此外,由式(3)知,相邻时刻的量测噪声分量vk和vk-1不相关。因此,随机噪声分量Vk的方差为:

式(5)即为增量量测方程,增量量测方程成功地消除了原来量测方程中存在的未知系统误差。
3 增量容积卡尔曼滤波
假定过程噪声服从高斯分布,根据贝叶斯滤波理论,状态估计的时间更新计算公式为:
其中,Rn表示n维实数空间;ΔZ1:k-1表示从第1时刻直到第k-1时刻所有增量量测值的集合;N(·)表示高斯分布。相应地,时间更新的协方差计算公式推导为:

假设预测量测的误差是零均值白噪声序列,通常假定其为高斯分布,则似然密度函数可以写为:

其中,预测增量量测值为:

相应的协方差矩阵为:


其中,状态向量和增量量测向量的协方差矩阵计算式为:

一旦接收到k时刻的量测值zk,则可以计算出该时刻的增量量测值Δzk,根据贝叶斯滤波方程计算状态向量的后验分布,即:

其中:

在噪声分布为高斯分布的假定下,贝叶斯滤波理论中的时间更新和量测更新过程中存在非线性函数和高斯概率密度函数乘积的积分形式,如式(6)、式(7)、式(9)、式(10)和式(12)所示,其中存在的关键问题就是要找出该积分的数值解法。下面介绍容积点积分方法。
考虑一个n维加权积分:

其中,f(x)是一个非线性函数;权值函数ω(x)是一个高斯密度函数,且对于所有x∈D,D为n维实数域,有ω(x)≥0。对于这类高斯加权积分可以采用数值积分的方法进行近似,即找出一组具有权值ωi的点集xi,通过加权求和的方式对积分I(f)进行近似:

在容积点积分方法中,使用球面径向规则获得一组点集及其权值。对于3阶球面径向规则,总共需要2n个点,这些点被称为容积点,其中,n表示状态向量的维数。根据球面径向规则,计算一个标准高斯加权积分的数值化近似公式为:


而[1]i表示对应序列中的第i个单位点。

对于式(1)和式(5)所表示的非线性增量系统,假设噪声分布服从高斯模型,可以采用容积点的方法计算贝叶斯滤波过程中的积分。假定状态向量初始值及其协方差0|0,P0|0已知,则根据k-1时刻的状态估计k-1|k-1及其协方差Pk-1|k-1,可得出k时刻的状态估计k|k及其协方差Pk|k。递推过程的时间更新步骤为:
Step 1 采用Cholesky或者奇异值方法分解协方差:

Step 2 根据式(20)中容积点χi的定义,计算容积点(i=1,2,…,m):

Step 3 根据式(20)计算预测状态容积点:

Step 4 估计预测状态:

Step 5 估计预测协方差:

递推过程的量测更新步骤为:
Step 1 对预测协方差矩阵进行分解:

Step 2 计算容积点(i=1,2,…,m):

Step 3 根据式(5)计算相应的增量量测容积点:

Step 4 估计预测增量:

Step 5 估计增量量测的新息协方差矩阵:

Step 6 估计互协方差矩阵:

Step 7 利用式计算卡尔曼滤波增益,利用式(14)和式(15)估计状态更新及其协方差矩阵。
4 仿真实验及结果分析
考虑单变量非稳态增长模型的强非线性系统[5]:
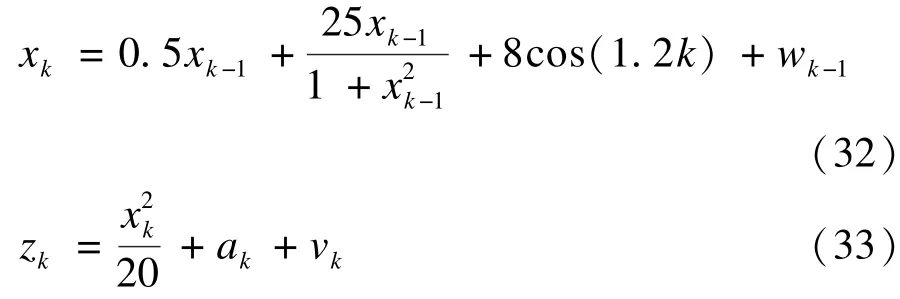
其中,wk和vk是k时刻不相关的过程噪声分量和量测噪声分量,分别服从均值为0方差为Q和R的高斯分布。在实验中取Q=1,R=1,初始状态x0|0=0,相应的初始协方差为P0|0=10。量测方程的系统误差ak=4为未知量。
为了使用标准容积卡尔曼滤波算法,忽略掉量测方程中未知的不确定分量ak,即假定ak=0。由于

因此增量量测方程中消去了量测系统的未知分量,此时采用增量容积卡尔曼滤波算法可以获得更好的滤波精度。为方便起见,假定vk和vk-1不相关,则增量量测方程中的噪声分量Vk服从高斯分布,且其均值为0,方差为2R。
分别采用标准容积卡尔曼滤波算法和增量容积卡尔曼滤波算法进行仿真,滤波结果如图1和图2所示。

图1 状态估计
由图1可知,增量容积卡尔曼滤波与标准容积卡尔曼滤波相比,精确度更高。图2是2种方法状态估计结果和真实结果之差。增量容积卡尔曼滤波的误差聚集于0值附近,而标准容积卡尔曼滤波误差幅度则较大。并不是任意时刻中的增量容积卡尔曼滤波误差都比标准容积卡尔曼滤波误差低,例如,在图2误差曲线中的第9步和第88步,本文算法的误差反而比较大。但是从整个结果来看,增量容积卡尔曼滤波比标准容积卡尔曼滤波滤波精度高。

图2 状态误差
采用增量容积卡尔曼滤波、标准容积卡尔曼滤波、增量扩展卡尔曼滤波和标准扩展卡尔曼滤波对上述例子重复运行10 000次,计算各种算法状态估计的均方根误差,其值依次为8.405 9,10.069 3, 10.734 4和12.5135。可知增量容积卡尔曼滤波误差低于标准容积卡尔曼滤波,增量扩展卡尔曼滤波误差低于标准扩展卡尔曼滤波,标准容积卡尔曼滤波误差略低于增量扩展卡尔曼滤波。上述结果表明,增量容积卡尔曼滤波能够成功消除量测方程中的系统误差,与增量卡尔曼滤波相比,能够获得更高的滤波精度。
5 结束语
本文在滤波系统的高斯假设下,结合3阶球面径向积分规则,提出了一种新的非线性增量滤波算法——增量容积卡尔曼滤波算法。该算法能够成功消除量测系统误差,滤波精度不但高于标准容积卡尔曼滤波,而且还高于增量扩展卡尔曼滤波算法。然而,由于算法中的容积点个数是状态向量维数的2倍,因此运算时间复杂度与增量扩展卡尔曼滤波算法相比有所提高。新算法滤波精度的提高是以时间复杂度为代价换来的。在通常情况下,容积点的选取采用3阶球面径向积分规则。如果采用高阶积分规则,使用更多的积分点,理论上可以获得更高的滤波精度,关于高阶容积卡尔曼滤波算法误差性能的研究是下一步需要探讨的课题。
[1] 韩崇昭,朱洪艳,段战胜.多源信息融合[M].2版.北京:清华大学出版社,2010.
[2] Julier S J,Uhlmann J K.UnscentedFiltering and Nonlinear Estimation[J].Proceedings of the IEEE, 2004,92(3):401-422.
[3] Arasaratnam I,Haykin S.Discrete-time Nonlinear Filtering Algorithms Using Gauss-Hermite Quadrature [J].Proceedings of the IEEE,2007,95(5):953-977.
[4] Norgaard M,Poulsen N K,Ravn O.NewDevelopments in State Estimation for Nonlinear System[J]. Automatica,2000,36(11):1627-163.
[5] Arulampalam M S,Maskell S,Gordon N,et al.A Tutorial on Particle Filters for Online Nonlinear/Non-Gaussian Bayesian Tracking[J].IEEE Transactions on Signal Processing,2002,50(2):174-188.
[6] Arasaratnam I,Haykin S.Cubature KalmanFilters[J]. IEEE Transactions on Automatic Control,2009,54(6): 1254-1269.
[7] Li Pengfei,Yu Jianping,Wang Mingjie,et al.The AugmentedForm ofCubatureKalman Filterand Quadrature Kalman Filter for Additive Noise[C]// Proc.ofIEEE Youth Conferenceon Information, Computing andTelecommunication.[S.l.]:IEEE Press,2009:295-298.
[8] Chandra K P B,Gu Dawei,Postlethwaite I.Square Root Cubature Information Filter[J].IEEE Sensors Journal, 2013,13(2):750-758.
[9] Arasaratnam I,Haykin S,Hurd R T.Cubature Kalman Filtering for Continuous-discrete Systems:Theory and Simulations[J]. IEEE Transactions on Signal Processing,2010,58(10):4977-4993.
[10] Leong P H,Arulampalam S,Lamahewa T A,et al.A Gaussian-sum Based Cubature Kalman Filter for Bearings-only Tracking[J].IEEE Transactionson Aerospace andElectronicSystems,2013,49(2): 1161-1176.
[11] 傅惠民,吴云章,娄泰山.欠观测条件下的增量Kalman滤波方法[J].机械强度,2012,34(1):43-47.
[12] 傅惠民,娄泰山,吴云章.欠观测条件下的扩展增量Kalman滤波方法[J].航空动力学报,2012,27(4): 777-781.
[13] 傅惠民,娄泰山,吴云章.无迹增量滤波方法[J].航空动力学报,2012,27(7):1625-1629.
[14] 傅惠民,娄泰山,吴云章.增量粒子滤波方法[J].航空动力学报,2013,28(6):1201-1207.
编辑 顾逸斐
Incremental Cubature Kalman Filtering Under Poor Observation Condition
MA Li-li1,ZHAO Tian-tian1,CHEN Jin-guang1,2
(1.School of Computer Science,Xi’an Polytechnic University,Xi’an 710048,China;
2.School of Electronic Engineering,Xidian University,Xi’an 710071,China)
In some engineering applications,there are some cases like the effect of environment,the instability of measurement devices.Large error comes into being from the measurement equation in the nonlinear filtering system.The standard nonlinear filtering algorithm cannot remove this kind of system error.This paper addresses this problem,assumes that process noises and measurement noises are subject to Gaussian distribution,establishes the incremental measurement equation using the difference between the adjacent measurements,and obtains the cubature points and its weights using the third-degree spherical-radial rule.The cubature points are employed to approximate the integrals in the Bayesian filtering process numerically,and the incremental cubature Kalman filtering is obtained.Simulation results show that the filtering accuracy of the incremental cubature Kalman filtering is not only better than that of the standard cubature Kalman filtering but also better than that of the incremental extended Kalman filtering.The new algorithm can eliminate the system error of the measurement equation successfully.
incremental measurement equation;incremental cubature Kalman filtering;poor observation condition; Kalman filtering;state estimation;deep space exploration
1000-3428(2014)10-0228-04
A
TP391
10.3969/j.issn.1000-3428.2014.10.043
国家自然科学基金资助项目(61201118);中国博士后科学基金资助项目(2013M532020);陕西省教育厅科研计划基金资助项目(14JK1304);国家级大学生创新创业计划基金资助项目(201310709006)。
马丽丽(1979-),女,讲师,主研方向:信息融合,目标跟踪;赵甜甜,本科生;陈金广,副教授、博士。
2013-09-09
2013-10-31E-mail:xamll@163.com
中文引用格式:马丽丽,赵甜甜,陈金广.欠观测条件下的增量容积卡尔曼滤波[J].计算机工程,2014,40(10):228-231,238.
英文引用格式:Ma Lili,Zhao Tiantian,Chen Jinguang.Incremental Cubature Kalman Filtering Under Poor Observation Condition[J].Computer Engineering,2014,40(10):228-231,238.
