基于模糊逻辑的两步卡尔曼滤波器设计

金 梅， 张志福， 金 菊， 于国辉， 李文超

（1.燕山大学河北省测试计量技术与仪器重点实验室，河北秦皇岛 066004；

2.河北工业大学土木工程学院，天津 300401； 3.秦皇岛视听机械研究所，河北秦皇岛 066000）

基于模糊逻辑的两步卡尔曼滤波器设计

金 梅1， 张志福1， 金 菊2， 于国辉3， 李文超1

（1.燕山大学河北省测试计量技术与仪器重点实验室，河北秦皇岛 066004；

2.河北工业大学土木工程学院，天津 300401； 3.秦皇岛视听机械研究所，河北秦皇岛 066000）

在对惯性运动跟踪系统的建模分析中，常采用基于计算机的集中式卡尔曼滤波算法进行数据处理。由于该方法存在算法复杂，处理数据速度慢等问题，难以在嵌入式系统中实现高速运动跟踪，提出一种基于模糊逻辑的自适应两步卡尔曼滤波算法。该方法根据人体不同的运动状态调整卡尔曼滤波器，实验结果证明所提的方法能够更好地估计各个传感器的测量精度，减少了运算量，并在一定程度上提高了滤波器的容错性能。

计量学；惯性运动跟踪系统；模糊逻辑；两步卡尔曼滤波

1 引 言

运动跟踪技术可以实时地测量人体各个关键部位的运动状态信息，为步态识别、影视制作和机器手臂交互控制等应用提供关键数据［1，2］。目前惯性运动跟踪系统主要使用惯性微机电传感器和磁力计实现角度估计，典型的组成结构是三轴陀螺仪、三轴加速度计和三轴磁力计的九自由度测量系统。因为微机电陀螺仪存在明显的固有偏差和噪声误差，因此姿态角的误差会时间而不断增长。另一方面，微机电加速度计测量值是重力加速度和运动加速度的总和，因此需要对运动加速度进行估计和处理；磁力计也会受到外界磁场的干扰，包括软磁和硬磁干扰，磁力计自适应误差补偿的同时，也需要准确估计外界磁场的干扰。

通过对惯性运动跟踪系统建模分析，人们设计了多种卡尔曼（Kalman）滤波算法，其中大部分是采用基于计算机的集中式卡尔曼滤波器［3］，为了进一步提高卡尔曼滤波的估计精度，人们先后提出了多种自适应调整方法［4，5］，尽管各种自适应滤波的实现方法有所不同，但都是根据信息序列，更多依靠统计特性，并不能准确地判别其实际的运动状态，这些不能准确地判别其实际的运动状态，同时这也存在一定的时间滞后性。

为了提高估计精度和减少运算量，提出一种适用于嵌入式系统的基于模糊逻辑的两步卡尔曼滤波算法，该法根据人体的运动状态实现卡尔曼的自适应调整，能够更好地估计各个传感器的测量精度，而且数据采集和姿态解算在各个模块内完成，避免了大量的数据传输，降低了运动跟踪系统的复杂性，使惯性跟踪技术得到进一步的普及应用。

2 载体的运动姿态

设计了惯性跟踪系统的测试模块，主要由HMC5883（Honeywell提供的弱磁干扰的AMR传感器），ADXL345（ADI公司生产的三轴加速度计）和L3G4200（意法半导体提供的三轴数字陀螺仪）组成，见图1；采用欧拉角表示载体的运动姿态，见图2。

图1 惯性跟踪系统测试系统

图2 欧拉角示意图

根据陀螺仪输出的各轴角速度（ωx，ωy，ωz），在已知K－1时刻欧拉姿态角的情况下，根据积分计算得到K时刻的导航坐标下各轴的角速度：

当加速度计处于静止状态下，加速度计输出载体坐标内的重力加速度［gx，gy，gz］，得到欧拉坐标内的俯仰角θ和横滚角φ：

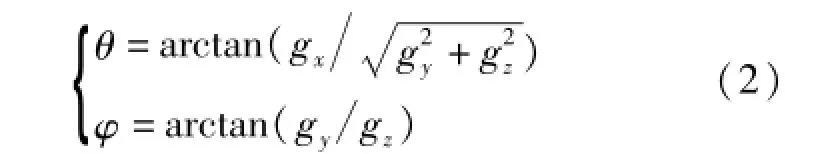
根据地磁场矢量可以估计出偏航角、俯仰角和横滚角。因为环境中的电磁干扰，采用地磁场计算俯仰和偏航角的精度很难得到保证，在此磁力计只用于计算和修正偏航角，载体坐标内的地磁场为［mxz，myz，mzz］，地理坐标X-Y平面内的地磁场为［mxi，myi，mzi］，偏航角（Yaw）ψ可由式（3）得出：

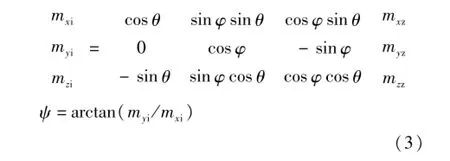
3 运动加速度处理

A.D.Young的人体运动模型将人体运动简化为刚体的圆周旋转运动［6］，Ji、Si分别是关节和传感器安装位置。假设某一关节的旋转角速度为ω，角加速度为α，旋转中心节点为p，可得p点的载体坐标内的运动加速度为：

式中lt和lr分别为切向加速度和径向加速度。将载体坐标的运动加速度转换到地理坐标内，可以建立全身的运动加速度估计方程：

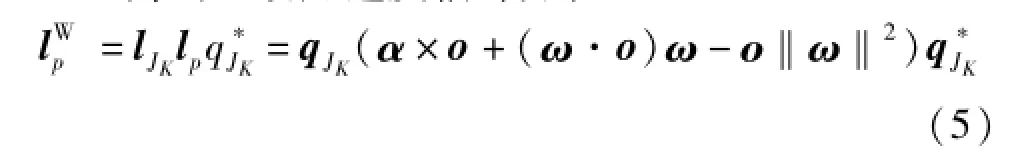
式中：lWp为地理坐标下旋转中心节点p的运动加速度；qJK为关节JK的姿态；q*JK为qJK的共轭四元数。

通过式（4）和式（5），可以估计X、Y、Z三轴的运动加速度值。估计的运动加速度可用来补偿和修正X、Y、Z三轴的重力加速度可信度。因为各轴重力加速度的可信度随着运动加速度的增加而降低，本文根据各轴的运动运动加速度分别处理三个轴向的加速度分量［7］。

4 基于模糊逻辑的自适应滤波器

4.1 惯性运动跟踪系统中的两步卡尔曼滤波

引入了2步卡尔曼滤波算法设计滤波器，见图3。2步卡尔曼滤波由两个子卡尔曼滤波器组成：第1步，进行俯仰角和横滚角的卡尔曼滤波。陀螺仪更新状态向量，根据修正后的重力矢量更新观测向量，构成2维的卡尔曼滤波器，具体如式（6），ΔT为采样间隔。

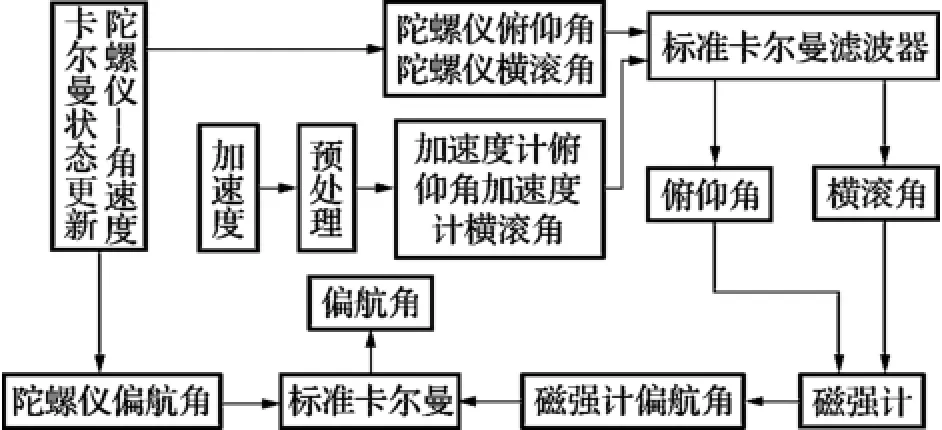
图3 基于两步卡尔曼的AHRS设计

第2步，进行偏航角的卡尔曼滤波。根据第1步的估计结果，将其代入地磁场矢量方程，即式（3），将其从载体坐标转换到地理坐标的平面内，得到偏航角的观测向量，陀螺仪更新偏航角的状态向量，构成了1维的卡尔曼滤波：

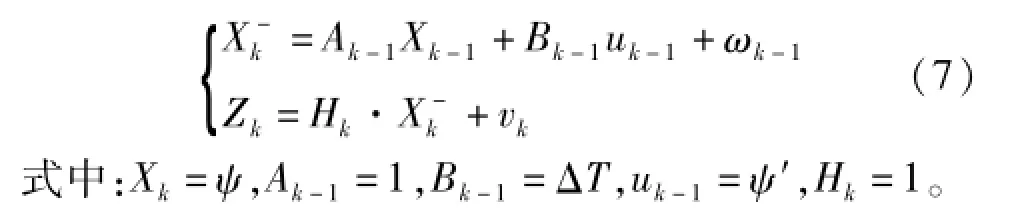
解耦后的两步卡尔曼滤波依次进行俯仰角、横滚角和偏航角的状态更新和角度估计。

4．2 基于模糊逻辑的自适应两步卡尔曼滤波器

卡尔曼滤波器是根据状态向量和观测向量的误差大小，进行权重的分配，而向量的误差大小则是由状态向量的方差矩阵Q和观测向量的方差矩阵R反映。状态向量和观测向量的误差共同组成了卡尔曼滤波的信息序列，为了准确地分析当前各个传感器的误差大小和载体的实际运行状态，本文将各轴向的角速度、运动加速度和外部磁场强度作为模糊逻辑的判断依据，并调整状态向量的方差矩阵Q和观测向量的方差矩阵R。根据模糊逻辑的判断结果，将信息序列包含的测量误差分配给Q、R。

基于模糊逻辑的横滚角和俯仰角的卡尔曼滤波器见图4。

陀螺仪更新的载体姿态误差，如式（8）。当载体处于不同运动状态时，加速度计测量俯仰角和横滚角的可靠性有所变化，如式（9）。θG和θA分别为陀螺仪和加速度计的俯仰角，ψG和ψA分别为陀螺仪和加速度计的偏航角，偏航角的卡尔曼滤波器如图5所示。

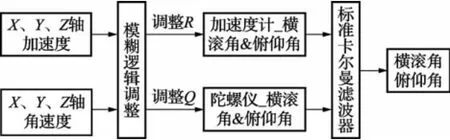
图4 横滚角和俯仰角自适应分散卡尔曼示意图

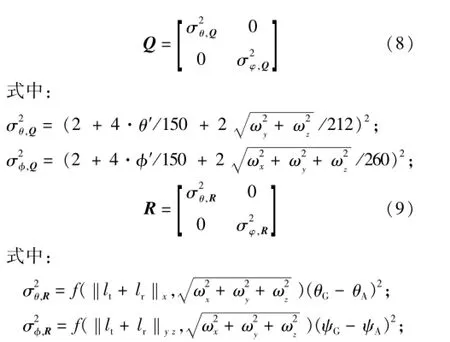
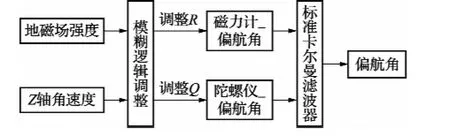
图5 基于模糊逻辑的偏航角自适应分散卡尔曼示意图

随着角速度的增加，陀螺仪的估计误差也会增加，包括零偏和累积误差，Q的自适应调整方程为：

矩阵R为磁场强度、角速度和信息间的方程，R阵的自适应调整方程为：

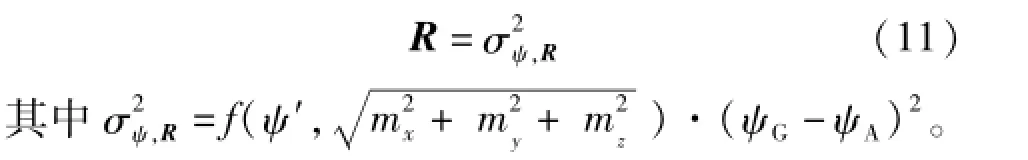
为化简式（9）和式（11），针对载体坐标内各轴向的角速度、运动加速度大小和地磁场矢量大小进行模糊逻辑状态识别，分别判断载体的运动状态，见图6。

图6中，SS、SL、MS、ML、LS、LL为模糊逻辑的6种状态，MF为隶属函数。根据式（5）可以估计各轴的运动加速度。式（9）的矩阵R调整方程，可以简化为：

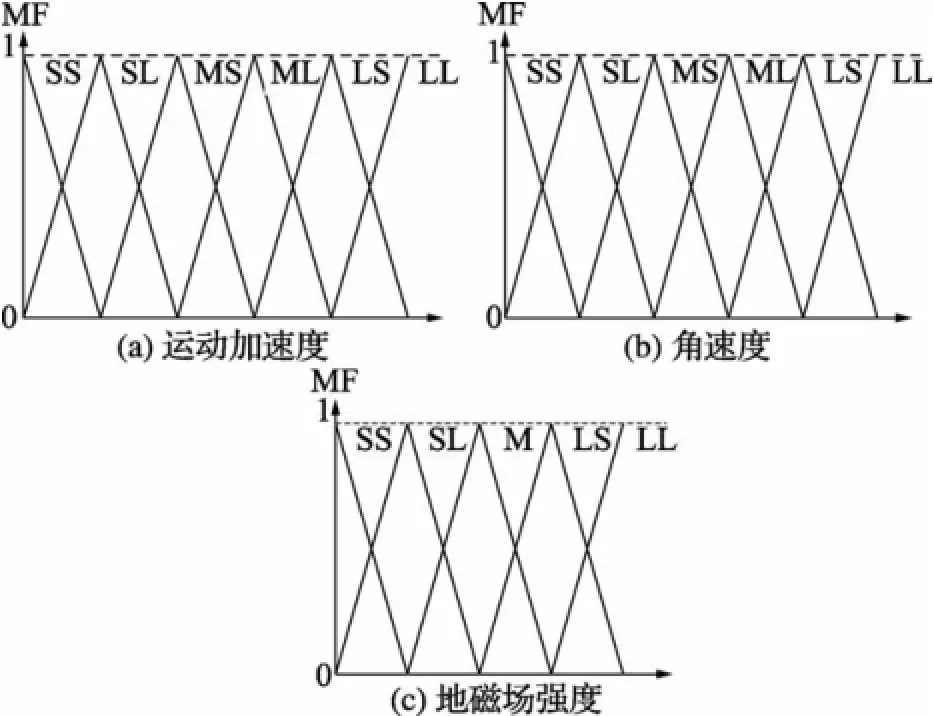
图6 模糊逻辑成员函数

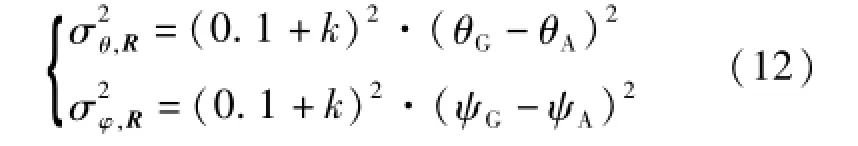
式中k为模糊逻辑输出，具体如表1所示。

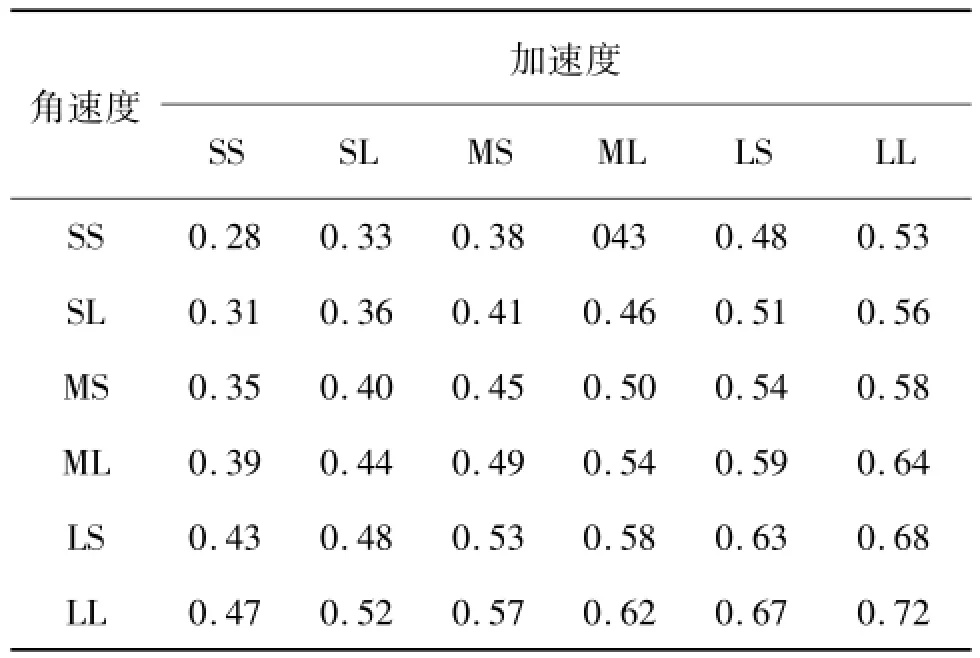
表1 加速度计和陀螺仪的k

根据式（3），代入俯仰角和横滚角的估计结果可以得到地磁场矢量估计的偏航角，根据模糊逻辑，将式（11）简化可得：

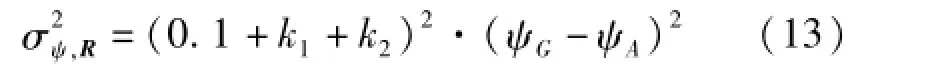
式中，k1，k2为模糊逻辑输出，具体值如表2、表3所示。

表2 磁力计和陀螺仪的k1

表3 磁力计和陀螺仪的k2

5 实验分析

将上述算法在MSP430F169（单芯片微控制器）编程，实现肢体的角度估计，结果通过UART总线按45 Hz发送到PC机。为测试两步卡尔曼滤波器的角度估计性能，设计4组实验。实验1和2中，IMU分别绕X、Y轴以100°／s旋转，测试各轴的估计精度。实验3和4中，对IMU施加电磁干扰和震动干扰，测试滤波器对外部干扰的故障检测和容错性能。

实验1中，IMU以100°／s围绕X轴旋转，实验结果如图7（a）。

实验2中，IMU以100°／s围绕Y轴旋转，实验结果如图7（b）所示。

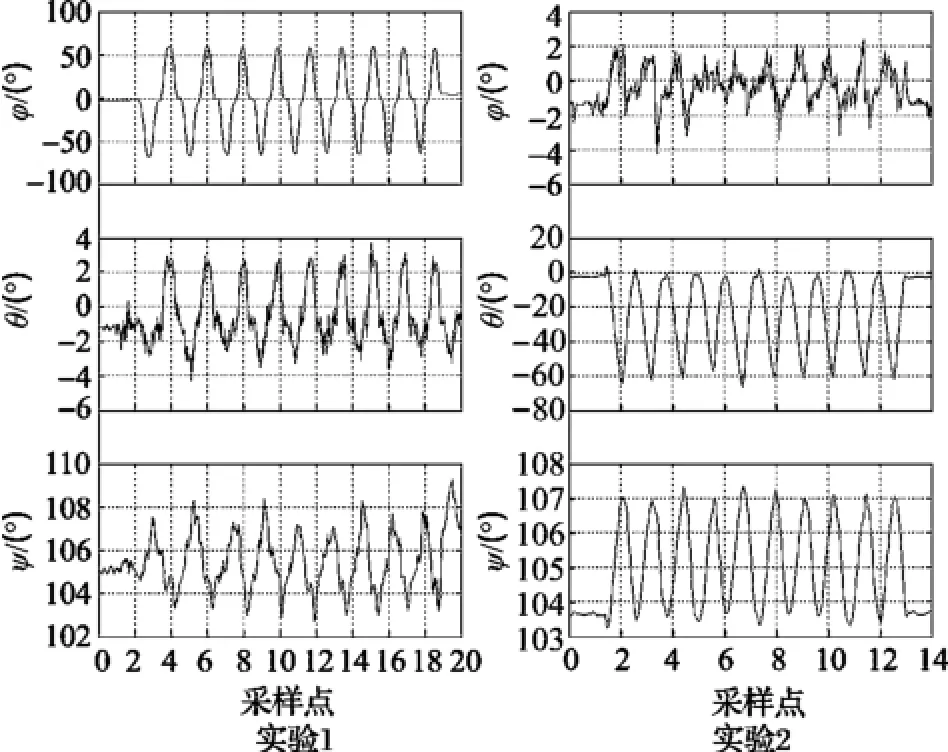
图7 实验1和实验2的测试结果

从实验结果可知，实验1中的横滚角和实验2中的俯仰角动态特性良好，滤波后曲线连续，能够实时的测量IMU的姿态角。实验1中，俯仰角和偏航角应该为恒定值；从实验结果看，俯仰角和偏航角的误差，在2.0°以内。实验2中，横滚角和偏航角和应该为恒定值；从实验结果看，横滚角和偏航角的误差，在2.5°以内。和横滚角和俯仰角相比，偏航角的角度估计方差偏大，因为偏航角的角度估计是基于横滚角和俯仰角的估计结果，另一方面，地磁场的干扰复杂，地磁场矢量的修正效果有限，所以偏航角的估计精度有所降低。

实验3中，将通话中的手机作为电磁干扰源，不断地在IMU周围平行移动，实验结果如图8所示。从实验结果可知，当周围存在明显的电磁干扰时，地磁场矢量解算的偏航角存在明显的角度波动，修正后的偏航角角度波动明显变小。另外，实验中惯性系统处于静止状态，输出的滚动角和俯仰角角度波动小于0.5°，基本可以认为是恒定值。因为受到外界电磁干扰的影响，偏航角的误差在5°左右，能满足实际要求。

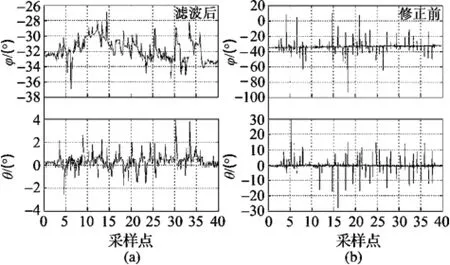
图8 实验3的测试结果

实验4中，将IMU静止平放，对平台进行间歇性的敲击震动测试，实验结果如图9所示，图9（a）为滤波后的滚动角和俯仰角，图9（b）为运动加速度修正前。可见震动IMU时，由重力加速度矢量直接解算的俯仰角和滚动角存在较大幅度的角度波动；滤波后有明显改善。

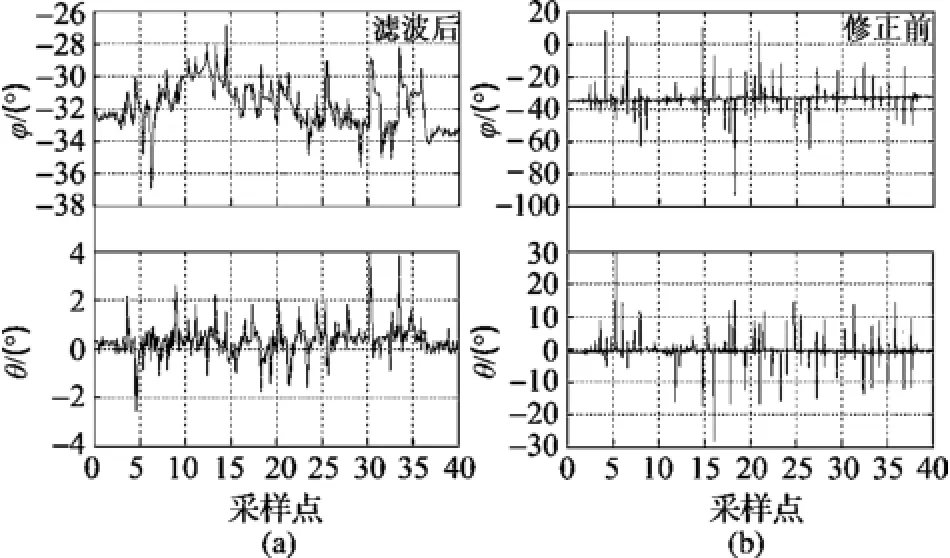
图9 实验4的测试结果

以上4组实验证明，本文提出的自适应两步卡尔曼滤波器，动态测量误差基本在2°以内，静态测量误差在0.5°内，对外界的电磁干扰和震动干扰有较好的容错能力，能够满足普通工程要求。

6 结 论

在人体惯性跟踪系统中，经常采用卡尔曼滤波器进行数据处理，为了进一步提高滤波器的估计精度并减少运算量，本文提出了基于模糊逻辑的两步卡尔曼滤波算法。该算法令每个滤波器独立并行工作，针对各个传感器的不同特性，进行分布式数据处理，从而简化了传统卡尔曼滤波的建模，同时引入了模糊控制算法，提高了系统的故障检测和隔离能力，减小容错计算负担。实验结果证明，该算法计算简单，具有较好的动态和静态估计效果。

［1］ Welch G，Bishop G，Vicci L，et al.The HiBall tracker：High-performance wide-area tracking for virtual and augmented environment［C］／／VRST'39，London，UK，1999，1－10.

［2］ Roetenberg D，Slycke P，Ventevogel A，et al.A portable magnetic position and orientation tracker［J］.Sensors and Actuators A，2007，135：426－432

［3］ Sutton R.Adaptive tuning of a Kalman filter via fuzzy logic for an intelligent AUV navigation system［J］.Control engineer practice，2004，12：1531－1539

［4］ Chaer W S，Bishop R H.A Mixture-of-Experts Framework for Adaptive Kalman Filtering［J］.IEEE TRANSACTIONS ON SYSTEMS，MAN AND CYBERNETICS—PART B：CYBERNETICS，1997，27（3）：452－464.

［5］ Escamilla-Ambrosio P J，Mort N.Multisensor Data Fusion Architecture Based on Adaptive Kalman Filters and Fuzzy logic Performance Assessment［C］／／ISIF，Annapolis，USA，2002，1542－1549

［6］ Young A D，Ling M J.Distributed Estimation of linear Acceleration for Improved Accuracy in Wireless Inertial Motion Capture［C］／／IPSN'10，Stockholm，Sweden，2010，256－267.

［7］ Yang Y，Miao L J.Adaptive federal Kalman filtering for SINS／GPS Integrated System［J］.Journal of Beijing Institute of Technology，2003，12（4）：371－375

Design of an Adaptive Two-step Kalman Filter Based on Fuzzy Logic

JIN Mei1， ZHANG Zhi-fu1， JIN JU2， YU Guo-hui3， LIWen-chao1
（1.Measurement Technology and Instrumentation Key Lab of Hebei Province，Yanshan University，Qinhuangdao，Hebei066004，China；2.School of Civil Engineering，Hebei University of Technology，Tianjin 300401，China；3.Audio-Visual Machinery Research Institute，Qinhuangdao，Hebei066004，China）

To analyze the modeling of the inertial／magnetic tracking system，the centralized Kalman filter algorithm depending on PC is often used to process the data.Because this algorithm is complex and the data processing speed is slow，it is difficult to realize high-speed motion tracking in the embedded system.An adaptive two-step Kalman filtermethod based on fuzzy logic for real-time motion tracking of human body is proposed.The parameters of Kalman filter are selfadjusted according to the differentmotion states of human body.Themethod can not only improve the estimation accuracy and fault-tolerant performance of the system to a certain degree，but also reduce thematrix dimension.

Metrology；Motion tracking；Fuzzy logic；Two-step Kalman filter

TB93

A

1000-1158（2014）04-0355-05

10．3969／j．issn．1000-1158．2014．04．11

2013-08-09；

2013-11-05

国家自然科学基金（61077071）

金梅（1977－），女，黑龙江明水人，燕山大学讲师，博士，主要研究方向为视觉伺服、智能控制及信号处理。meijin297＠126.com