基于模糊C均值聚类算法的金刚石砂轮磨粒边缘检测

高 琦， 崔长彩， 胡 捷， 叶瑞芳， 黄 辉

（华侨大学机电及自动化学院，福建厦门 361021）

基于模糊C均值聚类算法的金刚石砂轮磨粒边缘检测

高 琦， 崔长彩， 胡 捷， 叶瑞芳， 黄 辉

（华侨大学机电及自动化学院，福建厦门 361021）

基于模糊C均值（FCM）聚类算法将金刚石砂轮表面检测数据划分成金刚石和结合剂两个类别，以数据的质心初始化聚类中心，用迭代的方法分别求出相应的最优聚类中心和隶属度矩阵，通过选取合适的隶属度阈值以及两个聚类中心的欧氏距离阈值来区分金刚石和结合剂，确定磨粒边缘。为验证方法的可行性，对多组数据进行检测，并用模拟的砂轮表面形貌对此方法进行了评定，评定结果与设定值误差不超过2.0%。

计量学；边缘检测；模糊C均值聚类算法；金刚石砂轮；磨粒

1 引 言

准确地评价砂轮表面形貌对磨削机理研究、磨削过程优化及建模与仿真等具有重要意义，而准确的磨粒识别是砂轮形貌评价的关键［1］。磨粒的边缘检测在磨粒特征参数提取中起着重要的作用［2］，只有选用合适的方法将磨粒的边缘从测量数据中检测出来才能对一些重要的参数（如磨粒面积、等效粒径等）进行准确、有效的分析。金刚石砂轮表面形貌复杂，结合剂和金刚石磨粒形状及分布具有随机性和不规则性，因此识别金刚石和结合剂的边缘比较困难。

文献［3］应用数字图像识别技术识别砂轮磨粒，通过对CCD采集到的金刚石磨粒数字图像进行图像增强、二值化、滤波等图像处理，最终实现边界检测。文献［4］应用区域增长的方法，解决了数字图像识别方法中因磨粒反光强度不同造成的边缘数据丢失的问题。数字图像识别方法实时性好，易于计算，但识别磨粒边界是通过对物体和背景在图像特性上的某些差异（灰度、颜色等）来实现的［5］，而现在常用的三维测量方法，如触针式轮廓仪［6］，给出的测量结果多是砂轮表面高度，而不包含磨粒的颜色、纹理等能与结合剂相互区别的特征，因此数字图像识别方法在砂轮磨粒边缘检测中的应用有待改进。文献［1］应用数字滤波消除砂轮表面三维数字信息中的高频分量，然后提取金刚石磨粒的几何特征，提出了依据磨粒轮廓频率特征、磨粒间距和磨粒曲率半径识别金刚石磨粒的方法。该方法精度较高，但砂轮表面磨粒的形态有不确定性，有些磨损磨粒的特征条件达不到要求时会被忽略（如由于磨损而高度降低的磨粒），因此不能完整的反映磨粒边缘信息。

聚类分析是多元分析的一种，也是非监督模式识别的一个重要分支［7］。它将一个没有类别标记的样本按某种规则划分成若干个子集（类），相似的样本尽可能归为一类，而不相似的样本尽量划分到不同类中［8］。模糊聚类分析是聚类的研究主流，它得到的是样本属于某个类别的不确定程度［9］。磨粒和结合剂的形态具有不确定性，磨粒与结合剂的界限较为模糊，利用模糊理论能较好地描述砂轮磨粒与结合剂边缘不确定性的特点。

本文采用模糊C均值（Fuzzy C-means，FCM）聚类算法对三维数字信息进行处理分析，首先得到单数据行二维轮廓特征向量，并计算两个聚类中心（结合剂中心和磨粒中心），根据二维轮廓数据间的相似度，将具有相同属性的元素进行聚类划分，与磨粒属性差异大的数据对磨粒聚类中心隶属度较低的归为结合剂，对磨粒中心隶属度高的数据则归为磨粒，同时计算两个聚类中心的距离，距离小于设定阈值的被归为结合剂，区分了单行数据中的结合剂和磨粒。通过对每行数据进行分析得到砂轮三维表面形貌中多颗磨粒的边缘。该方法能够得到较为精确和完整的磨粒边缘，对于磨损的磨粒同样具有很好的检测效果。

2 FCM聚类算法原理

FCM聚类算法是一种代表性的模糊聚类算法，分类数给定，首先初始化聚类中心，计算样本中每个元素对于聚类中心的隶属度，然后通过若干次迭代反复修改聚类中心和隶属度矩阵，最终算法的迭代序列或其子序列收敛到目标函数的局部极小点，得到每个元素相对于某个聚类中心的最终隶属度，并以此寻找出对事物的最佳分类方案。

式中：n是样本元素个数；s是数据的维数；c是聚类中心数；m是模糊指数；dtj是样本点aj和聚类中心vt的欧氏距离；utj是第j个样本属于第t个聚类中心的隶属度，t＝1，2，…c；U是隶属度矩阵，V是聚类中心矩阵。FCCA就是求使聚类目标函数最小化的模糊划分矩阵U和聚类中心V。

在迭代求目标函数J的过程中，可通过以下公式（5）和（6）不断更新隶属度和聚类中心矩阵。

具体算法步骤如下［10］：1）根据具体问题，确定c，初始化vt，确定m的值；2）根据公式（4）计算dtj并计算U以及初始的目标函数值J（0）；3）根据公式（6），计算新的聚类中心，根据公式（4），（5）分别计算新的欧氏距离和隶属度函数，根据公式（1）计算新的目标函数值J（k），k为迭代次数，初始值为1；4）若||J（k）－J（k－1）||＜ε（允许误差），算法停止，否则返回步骤3），继续迭代，令k＝k＋1。

3 金刚石砂轮磨粒边缘检测

3.1 金刚石砂轮表面数据过程特征及提取

选用SDC120（120粒度）青铜结合剂金刚石砂轮，规格为100 D×10 T×5 X×31.75 H；测量仪器选用LSM700共聚焦显微镜，采样数据总数为508× 508，X与Y方向的采样间隔均为1.25μm。图1为共聚焦显微镜所测到的金刚石砂轮表面形貌的三维轮廓图（a）和俯视图（b）。

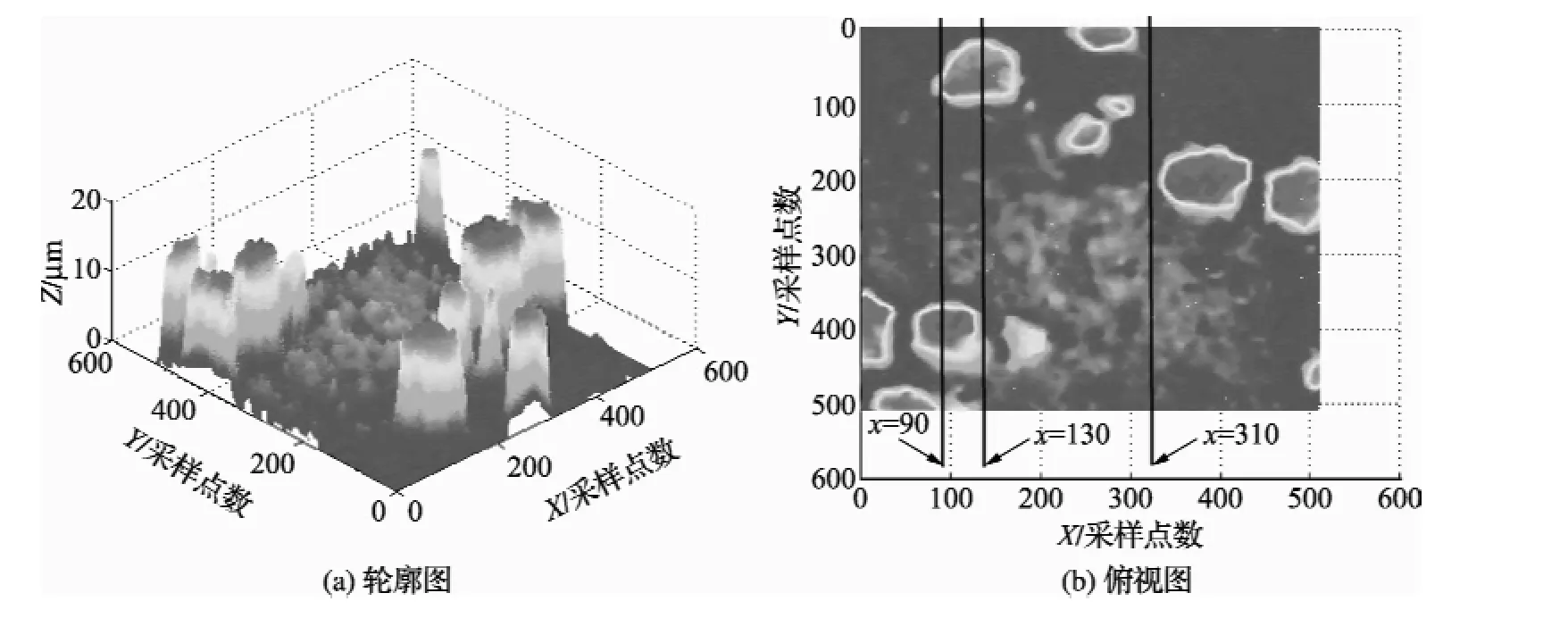
图1 砂轮表面三维轮廓图和俯视图

砂轮表面三维形貌可用Z（x，y）表示（x，y）坐标处的轮廓高度值。其中x、y是相互独立的变量，表示该表面的采样点坐标。为使阈值的选取更具有普遍适用性，先对高度数据进行归一化处理。

由图1（a）可知，砂轮表面磨粒和结合剂各自的轮廓高度变化规律是不相同的，是区分金刚石磨粒和结合剂的依据。因此选取表面二维高度、高度变化速度和加速度这3项为表面数据的过程特征向量。过程特征向量的求解方法如下：

假设砂轮表面某行第n点处高度数据的数值为h（n），n＝1，…，N，N为采样点数，N＝508。第n点处高度数据的变化率为h′（n）（即变化速度），h＇″（n）为变化加速度，则金刚石砂轮表面数据过程特征［11］可表示为：

其中T表示向量的转置。

第（n＋δ）个扫描点处的数据可近似地用n处的过程特征表示：

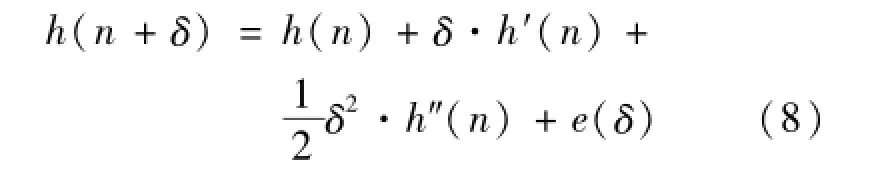
其中e（δ）为估计误差。根据估计误差最小的原则，应使在扫描点n附近的e2（δ）最小。

为减少程序的运算量，选取窗函数w（δ）来计算误差平方和，取δ∈［－l，l］，l为正整数，则加窗目标函数G为：

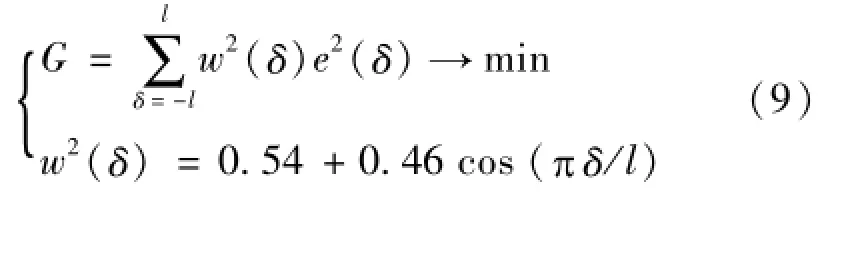
这是一个最优化问题，解得，

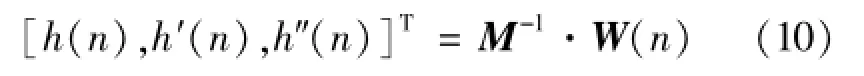
其中，

l的取值对特征过程向量有很大的影响。l较大，G的值越接近真实的误差平方和e2（δ），特征向量能较好地反映数据变化过程，但运行量较大；l较小，造成估计误差数据截取的误差加大，过程特征向量受随机误差干扰较大。l＝3时所得特征向量如图2所示。

随机提取一行（图1（b）x＝130行）高度数据，如图2（a）所示，较高的为磨粒部分，较低的为结合剂，由图2（a）、图2（b）、图2（c）可知，此行磨粒和结合剂在高度数据以及高度数据变化速度、加速度上存在着明显的不同，在图2（d）中，数据明显分成了两个部分，根据数据特点可知原点附近的部分为结合剂，远离原点的部分为磨粒，表明所选特征向量能很好地反映表面数据的变化规律。

3.2 聚类中心的确定

选取见图1（b）中第130行数据，由公式（10）、（11）、（12）求得特征向量H＝［h1，h2，h3…hN］3×N，并且初始聚类中心矩阵V＝［v1，v2］3×2，H是包含磨粒高度、高度变化速度以及加速度信息的特征过程向量集合，v1，v2分别是结合剂、磨粒的聚类中心。由聚类分析可知，随机选取不同的聚类中心，将会得到不同的聚类结果［12］，而且迭代结果易陷入局部极小的问题。为提高算法准确性，分别求取磨粒和结合剂部分数据的质心作为初始化的v1，v2。此方法有目的和有规则地初始化聚类中心，能在一定程度上避免随机初始化聚类中心所造成的算法收敛于局部极小的问题。

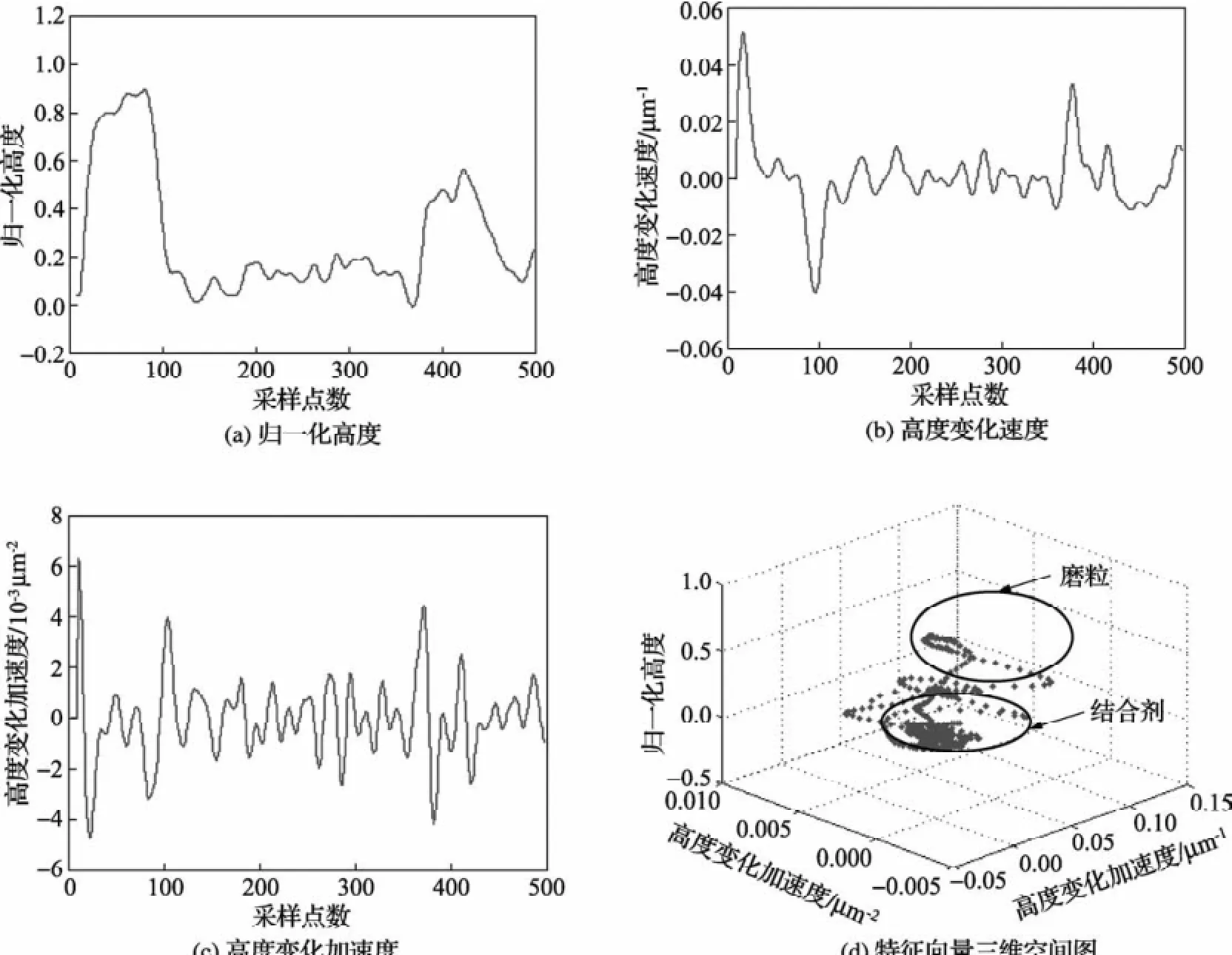
图2 图1（b）中第130行数据特征向量图

模糊指数m控制分类矩阵的模糊程度，但m的选取尚缺乏理论指导。本文采用文献［13］提出的基于目标函数拐点的方法来确定m的取值。文献［13］提出目标函数存在拐点，并验证了该拐点对应的m值可作为合适的模糊指数，目标函数的拐点恰好是目标函数导数的极小值点。由公式（14）、（15）计算数据对于初始化的聚类中心的dtj和U＝［utj］2×N，根据公式（13）构造目标函数，计算Jd＝∂J（U，V）／∂m的值，其中m≥1，计算结果如图3所示，最终第130行数据合适的m值为2．5。

同理计算所有行的最优m值，最终确定m值的区间为［2，3．5］。为使参数更具有适用性，同时考虑文献［14］所提出的m最佳取值区间为［1.5，2.5］，最终选择m＝2.5为统一参数值。

砂轮磨粒的边缘检测的关键就是寻找最优的聚类中心V，使其满足目标函数J为最小。

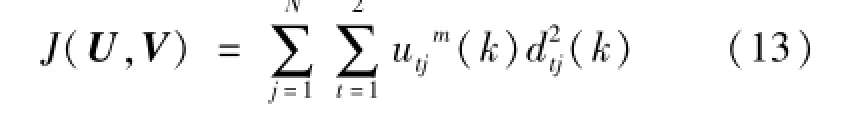
图3 图1（b）中第130行数据拐点法所求m值

式中：1≤t≤2；1≤j≤N。

由公式（14）、（15）计算dtj和U＝［utj］2×N，根据U和公式（16）获得新的聚类中心，将公式（13）、（14）、（15）、（16）进行迭代计算解决目标函数最优化问题，为简化计算，给定允许误差ε＝0.00001，在满足||v（k）－v（k－1）||＜ε时停止迭代。图4为图1（b）中第130行数据的允许误差与目标函数迭代结果图，目标函数在经过4～6次迭代后迅速收敛，而允许误差迭代完成时目标函数已经收敛。最终计算得到两个最优聚类中心。

图4 允许误差与目标函数迭代结果图

通过循环运算，得到每一行的最优聚类中心，并分别计算每行数据点对于两个聚类中心的隶属度，为后续边缘检测做准备。

图5和图6中标记了数据特征向量最优聚类中心以及作为初始化聚类中心的质心，计算得到的两个聚类中心在特征向量图的位置与质心的坐标基本一致。图7为图1（b）第90行和第130行数据隶属度曲线，由图可知，结合剂聚类中心隶属度曲线与磨粒聚类中心隶属度曲线正好相反，如图7（a）和（b）、图7（c）和（d），因此只分析数据相对磨粒聚类中心的隶属度曲线。

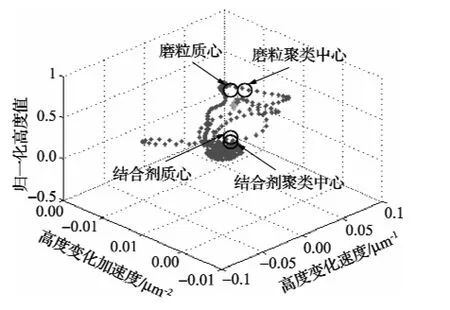
图5 图1（b）中第90行数据质心和最优聚类中心

3.3 边缘检测原则和结果分析

砂轮表面每一个数据点分别对于结合剂和金刚石两个聚类中心存在着隶属关系，因砂轮表面磨粒和金刚石的差异，隶属关系比较明显，故选取隶属度的阈值成为区分金刚石磨粒和结合剂的第一原则。

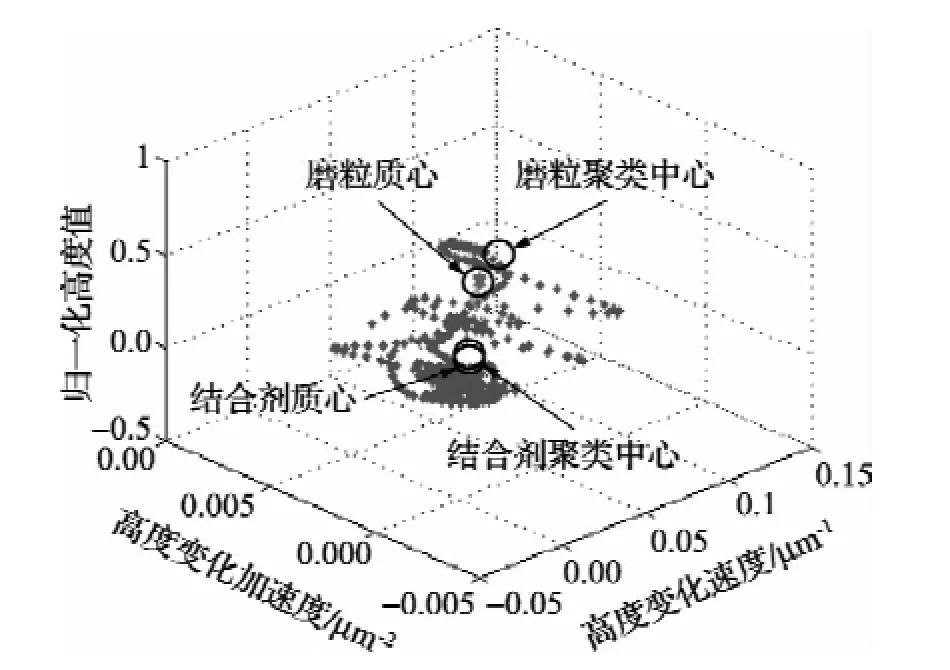
图6 图1（b）中第130行数据质心和最优聚类中心

对于只存在结合剂的数据行，如图1（b）第310行，由于数据分布比较集中，只有一个质心，最终只有一个聚类中心生成，见图8。图9是所有行磨粒与结合剂聚类中心的dtj示意图，从图中可以看出，由于金刚石砂轮表面磨粒和结合剂高度分布的随机性，每行两个聚类中心的dtj是不一致的，观察发现当磨粒高度较低时，聚类中心的dtj较小，而对于只存在结合剂的行由于只有一个聚类中心，dtj为0。因此，两类聚类中心的dtj成为除去结合剂行数据的干扰的第二原则。

由于金刚石砂轮表面磨粒的形态与分布的随机性以及结合剂不规则形状的影响，精确定位磨粒的边缘很困难。基于以上两个原则，通过对实验结果的观察和分析来找到区分磨粒和结合剂的两个阈值可以较为准确的确定磨粒边缘。

如图7所示，图1（b）第90行数据点对于结合剂和磨粒的隶属关系的区分比较明显；第130行存在一颗较大的磨粒和另一颗因磨损而存在较缓边缘的磨粒，磨粒较缓变化的边缘部分因高度、高度变化速度和加速度均较小，会出现对磨粒隶属度较低的问题，因此必须选取合适的阈值来区分磨粒和结合剂。

经过大量实验并分析，初步选定阈值为0.8，当数据点对于磨粒聚类中心隶属度大于0.8时，可判定数据点所在的位置完全属于磨粒部分，当数据点对于磨粒聚类中心隶属度小于0.2时，判定数据点所在的位置属于结合剂；对两类聚类中心的隶属度阈值0.2和0.8之间的部分，考虑到由磨粒顶部到结合剂并不是一个突变过程，均存在一定的斜率，而且还会存在磨粒磨损造成的斜率很小的渐变过程，因此可以判定0.2和0.8中间的部分是磨粒，应该与磨粒相关联。综上所述，磨粒与结合剂的边界应是隶属度为0.2的数据点的位置，每行数据点对于本行磨粒聚类中心隶属度大于0.2的均认为是磨粒，由此区分磨粒与结合剂。

图9中第206、300、450行附近dtj最小，并存在dtj＝0的情况，因此可以断定是结合剂行，从图中数据点206行数值选定dtj阈值为0.17，dtj小于0.17均为结合剂行。

图7 图1（b）数据选择行隶属度曲线

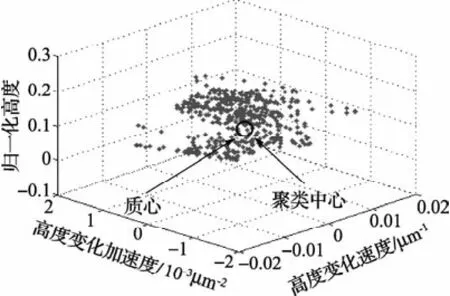
图8 图1（b）第310行数据质心和聚类中心

综上所述，区分磨粒和结合剂的阈值选择是：（1）表面高度数据对磨粒聚类中心隶属度大于0.2；（2）所在行两类聚类中心dtj大于0.17。

将符合条件的数据点的值置1，其余置0，生成二值图像，见图10；绘制二值图像轮廓即可得到边缘，见图11。

为验证方法的可行性，选取多组采样数据进行磨粒边缘处理。第一组砂轮磨粒表面形貌及其磨粒边缘轮廓如图12、13所示。第二组砂轮磨粒表面形貌及其磨粒边缘处理轮廓如图14、15所示。

图9 磨粒与结合剂聚类中心的dtj

图10 图1对应的磨粒边缘二值图像

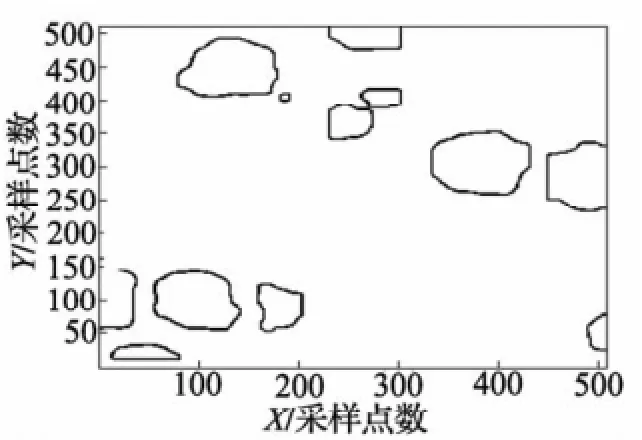
图11 图1对应的磨粒边缘轮廓图

图12 砂轮表面形貌俯视图

4 实验验证

采用模拟砂轮表面的方法，模拟120＃金刚石砂轮，基粒尺寸为125～100μm，将磨粒简化为球形，用高度在0～5μm范围的随机表面模拟砂轮表面结合剂，参数是：（1）表面面积：823μm×823μm，磨粒粒径100μm；（2）结合剂高度变化是0～5μm的

图13 与图12对应的边缘轮廓图

图14 砂轮表面形貌俯视图

图15 与图14对应的边缘轮廓图

随机值，磨粒出露高度20μm；磨粒间距100μm。

图16为未加噪声的形貌图，由16个半球组成阵列，模拟砂轮磨粒。图17为加噪声后的形貌图表面，所加高度一定的随机信号模拟结合剂，由于随机表面高度变化已知，半球的模型参数已知，因此可以计算出结合剂最高点处模拟磨粒边缘所围成的面积，通过理论面积和实际面积的比较，来计算算法的误差。图18是算法检测到的磨粒边缘和分布。

图16 未加噪声的形貌图

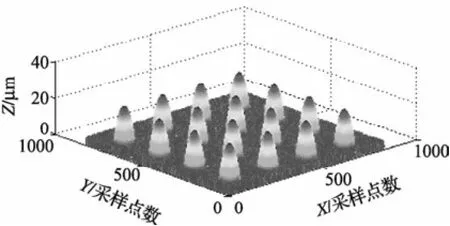
图17 加噪声后的形貌图

图18 检测到的磨粒边缘和分布

理论上每颗磨粒边缘围成的面积为5 026.55 μm2；通过程序检测到的每颗磨粒的面积为5013 μm2。16个模拟磨粒经边缘检测后得到的面积及误差见表1。由表1知，边缘检测得到的最大面积为4 987μm2，误差为0.52%，最小面积4 931μm2，误差为1.64%，在一定程度上说明了算法的精度。

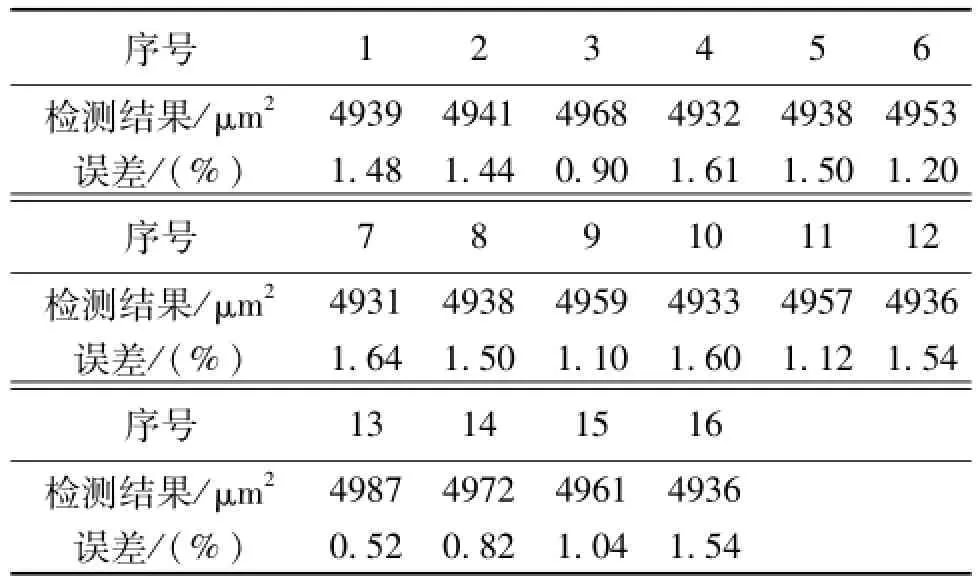
表1 检测结果

5 结 论

本文将模糊C均值聚类算法应用到砂轮表面磨粒的边缘检测，直接对测量仪器产生的三维数据进行处理，并且适用于磨损后的砂轮表面，能有效地区分磨粒与结合剂。但由于砂轮表面情况较为复杂，加上表面形貌检测仪器的各种误差，实际检测到的边缘与实际砂轮的边缘会有一些出入。同时，由于应用了聚类的方法，将表面数据强制分为了两类，这在隶属度阈值选取上难免存在偏差。但在实际应用中此种方法检测出磨粒的边缘与实际测量到的基本接近，并能检测出普通方法不能很好识别的较缓的边缘。

［1］ 霍凤伟，金洙吉，康仁科，等.细粒度金刚石砂轮表面磨粒识别研究［J］.大连理工大学学报，2007，47（3）：358－362.

［2］ 熊菲，周新聪，严新平.边缘检测技术在磨粒参数特征提取中的应用［J］.材料保护，2004，37（7）：171－173.

［3］ 张秀芳，于爱兵，贾大为，等.应用数字图像识别法检测金刚石磨粒的形状与粒度［J］.金刚石与磨料磨具工程，2007，（1）：47－49.

［4］ Lachance S，Bauer R，Warkentin A.Application of region growing method to evaluate the surface condition of grinding wheels［J］.International Journal of Machine Tools＆Manufacture，2004，44（7－8）：823－829.

［5］ 贾大为，于爱兵，张秀芳，等.应用数字图像识别技术检测金刚石砂轮磨粒的凸出高度［J］.工具技术，2006，40（12）：77－79.

［6］ Bulter D L，Blunt L A.The characterisation of grinding wheels using 3D surfacemeasurement techniques［J］.Journal of Materials Processing Technology，2002，127（2）：234－237.

［7］ 刘蕊洁，张金波，刘锐.模糊C均值聚类算法［J］.重庆工学院学报（自然科学），2008，22（2）：139－141.

［8］ 田慧欣，毛志忠.软测量建模中的过失误差检测新方法［J］.计量学报，2009，30（4）：374－377.

［9］ 贾丙静，王传安，宋雪亚.模糊C均值聚类算法的改进研究［J］.淮阴师范学院学报（自然科学），2011，10（3）：226－229.

［10］ 张慧哲，王坚.优化初始中心的模糊C－均值（FCM）算法［J］.计算机科学，2009，36（6）：206－209.

［11］ 张认成，杜建华，杨建红.火灾早期过程特征提取与火灾源识别方法［J］.安全与环境学报，2010，10（2）：152－156.

［12］ 丁志华.表面粗糙度几何特征的模糊聚类分析［J］.计量学报，1989，10（3）：231－235.

［13］ 高新波，裴继红，谢维信.模糊C均值聚类算法中加权指数m的研究［J］.电子学报，2000，28（4）：80－83.

［14］ Pal N R，Bezdek JC.On cluster validity for the fuzzy c-meansmodel［J］.IEEE Trans.Fuzzy Systems，1995，3（3）：370－379.

Grain Edge Detection of Diam ond Grinding Wheel Based on a Fuzzy C-m eans C lustering Algorithm

GAO Qi， CUIChang-cai， HU Jie， YE Rui-fang， HUANG Hui
（College of Mechanical Engineering and Automation，Huaqiao University，Xiamen，Fujian 361021，China）

Based on a fuzzy C-means（FCM）clustering algorithm，the height data set of ameasured grinding wheel surface is classified into two fuzzy clusters，which are named as“grain”and“bond”respectively.The clusters centers are initialized with the centroids of the classified data first，and then the most optimal cluster centers and the membership matrix are obtained with an iterative strategy.By choosing appropriate thresholds of the membership degree and the Euclidean norm of the two cluster centers，the edge of grains is determined.Themethod is validated with experiment.For further analysis，an evaluation is carried out by applying thismethod to a simulated grinding wheel surface，the results of which show that the error of thismethod is less than 2.0%.

Metrology；Edge detection；Fuzzy C-means clustering algorithm；Diamond grinding wheel；Grain

TB92

A

1000-1158（2014）04-0315-08

10．3969／j．issn．1000-1158．2014．04．03

2013-05-21；

2013-11-12

国家自然科学基金（51235004，51075160）；教育部新世纪优秀人才支持计划（NCET-10-0116）

高琦（1987－），男，河北保定人，华侨大学硕士研究生，主要研究方向为智能测控仪器与测控方法。qingtongjian1987＠163.com崔长彩为通讯作者。cuichc＠hqu.edu.cn