自适应插值算法在图像修复中的应用研究

马 敏， 赵 亮， 王化祥

（1.中国民航大学航空自动化学院，天津 300300； 2.天津大学电气与自动化工程学院，天津 300072）

自适应插值算法在图像修复中的应用研究

马 敏1， 赵 亮1， 王化祥2

（1.中国民航大学航空自动化学院，天津 300300； 2.天津大学电气与自动化工程学院，天津 300072）

针对BSCB模型速度慢、整体变分模型易产生阶梯效应的缺点，提出了一种基于扩散率函数的自适应插值算法。该算法利用待修复像素点周围的已知像素点的梯度权函数和距离权函数，对未知像素点进行赋值。实验结果显示：将该算法应用到灰度图像和彩色图像的修复中，与传统算法相比所需运算时间短，视觉效果较好，定量评价指标（峰值信噪比）也证明了该算法的有效性。

计量学；图像修复；偏微分方程；扩散率函数；自适应插值

1 引 言

图像修复是指根据已知信息对数字图像中丢失、破损的部分进行还原修复，以恢复其完整性和原有的视觉效果［1］。图像修复可用于修复图像划痕、去除多余物体以及文物保护等多方面，主要有基于纹理和基于非纹理的修复方法［2］。Criminisi等提出了基于纹理的图像修复方法，在未受损图像中寻找与受损模块最为匹配的修复模块并填充到受损区域内，从而实现图像的修复［3，4］，该方法修复过程耗时大、效率低。基于非纹理的图像修复的最新方法是基于偏微分方程的方法，包括Bertalmio等人在2000年引入了BSCB模型，Chan和Shen等人基于偏微方程提出了整体变分（total variational，TV）和曲率驱动方法。这类算法可以保持边缘同时去除噪声，但是难以得到高效、稳定的修复模型［5］。文献［6］沿Sobel算子确定的边缘方向进行自适应插值。文献［7］将逆梯度运算融入传统的双线性与双三次插值方法中，实现了图像边缘的锐化。这些插值方法虽可以得到较高的信噪比，但总体来说，这些图像修复方法运行比较缓慢，且难以恢复纹理细节。

图像的修复问题实质上是图像插值问题，对图像中已知像素的灰度值采用不同的距离权函数和梯度权函数进行运算，并对其赋值，从而得到未知像素的灰度值［8］。针对图像划痕等小面积修复情形，本文提出一种基于扩散函数的自适应插值算法（Adaptive Interpolation，AI）的修复模型，并进行算法实验，取得了较好的结果。

2 扩散率函数

作为数学物理模型，热传导方程表示一种传热过程。它属于线性偏微分方程，也被称为扩散方程［8］。图像的热传导平滑方程为

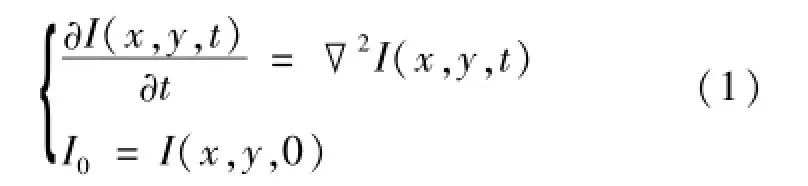
式中方程的初始条件为I0＝I（x，y，0），通常为输入的原始图像。∇2为图像拉普拉斯算子。由于热传导方程所描述的是各向同性的扩散过程，所以在图像平滑过程中，其定位特性较差，在大尺度上所保留的图像特征的空间位置会发生漂移，造成区域边界的模糊。针对这一问题，Perona和Malik提出了扩散率可变的各向异性扩散方程［9］，

式中：div为散度算子，c（x，y，t）为扩散率函数，∇为梯度算子，I0为方程的初始条件。扩散率函数是以像素点的梯度||∇I（x，y，t）|| 为自变量的单调下降函数，

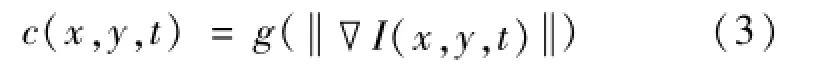
其中g（s）为单调下降函数。对于边界点等梯度比较大的像素点，扩散率较小，从而平滑功能会减弱，而当灰度值变化较平缓时，梯度值较小，扩散率则会比较大。实际应用中，扩散率函数通常选择为

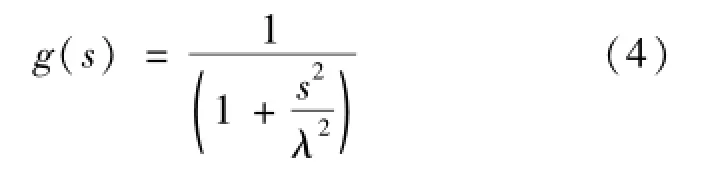
式中参数λ用来区分需要不同平滑强度的区域。

3 算法描述

文献［8］提出了一种图像插值放大算法，其主旨是用未知像素周围原始像素灰度值的加权和来决定待确定像素的灰度值，而各个原始像素的权值由图像在这一点的归一化导数值和它与被插像素之间的距离控制，并且原始像素点与内插像素距离越近，对它的影响就越大。假设插入的像素为α，在α附近有4个原始像素分别为α1，α2，α3，α4，它们之间的位置关系如图1所示。

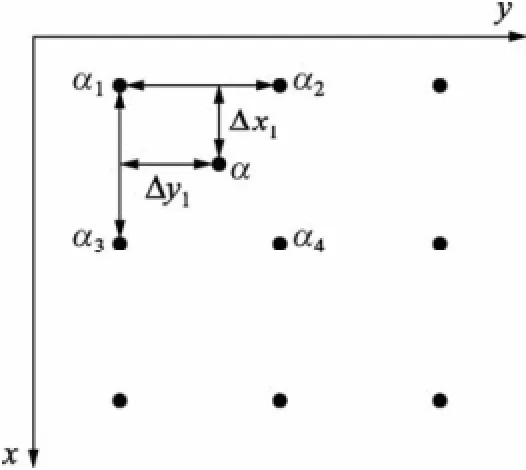
图1 α与αi（i＝1，2，3，4）的位置关系

若用Δxi表示α与αi（i＝1，2，3，4）的水平距离，用Δyi表示两者垂直方向的距离，则αi对α的影响权值D可以表示为：

本文提出一种将自适应插值用于图像修复的方法，分别求取待修复区域像素点周围的已知像素点的梯度权函数和距离权函数，对未知像素点进行赋值。

假设图I表示一幅受损的灰度图像，I（x，y）是像素点（x，y）的灰度值，D表示图像I中待修复区域。在插值过程中，应充分利用已知像素信息以保证像素值估计的准确性，同时要权衡算法的运算量，因此本文选用了5×5邻域来为像素点赋值，如图2所示。

图2 像素（i，j）的5×5邻域示意图

对于区域内一点（i，j），其灰度值I（i，j）由其5 ×5邻域内已知像素的灰度值决定，表达式为式中m和n不同时为0。W为各个像素点的梯度权函数，S为各个像素点的距离权函数，距离权函数S的确定引用文献［7］中的方法

式中Δx（u，v）和Δy（u，v）分别为待确定像素点（u，v）与其邻域像素点（i，j）之间的垂直距离和水平距离。

由于梯度是表征像素是否在平滑区域的一个重要物理量，本文的另一个权值引用P-M各项异性扩散模型中的扩散率函数：

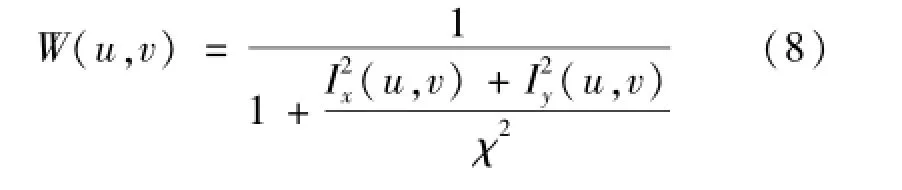
式中Ix（u，v）和Iy（u，v）分别为图像在像素点α处垂直方向和水平方向的一阶导数。将距离权函数式（7）与梯度权函数式（8）带入式（6）即可计算出插入像素点的灰度值。式中λ为待定参数，根据图像的具体情况取值，λ值越小，越趋向于对边缘的增强；λ值的增大可加强对图像的平滑作用。一般取χ＝3修复效果较好。

基于扩散率函数的图像修复算法主要步骤如下：

1）输入待修复图像I和破损标记mask，其中，mask表示待修复区域；

2）将破损区域内像素点置0，其余置1；

3）对于待修复区域内的每个像素，计算出其5 ×5邻域内所有已知像素的距离权值和梯度权值。

4）利用式（6）～式（8）求出待修复像素点（m，n）的灰度值I（m，n）；

5）重复步骤2）～步骤4），直到所有未知像素均被确定，输出修复后的图像I。

4 实验及结果分析

本文以MATLAB2009a为平台，在PC机（Intel（R）Core（TM）2 Duo CPU E4500，2.20 GHz，1 G内存）上对自适应插值算法进行实现，取参数λ＝3，并与经典的的BSCB算法和基于TV模型的图像修复方法进行比较。

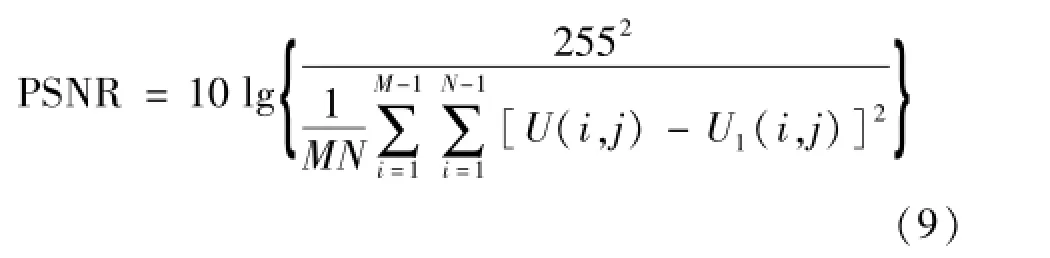
本文采用峰值信噪比（PSNR）、耗时2个指标对所修复图像进行科学的评估。峰值信噪比（PSNR）为：式中：U为原图像；U1为修复后的图像；M和N分别表示图像的行值和列值。在图像修复中，PSNR值越大，说明修复效果越好。

图3 Lena图像修复划痕效果比较

图3是用BSCB算法，TV算法和AI方法分别处理带划痕Lena图像的对比试验。从表1中可以看到本文的方法耗时为5.14 s，远小于BSCB算法，相应的PSNR的数值也较大，修复质量较好。TV的算法虽然时间上略占优势，但对lena帽子上划痕的修复存在错误的修复块，且边缘处不是很清晰。AI方法修复的图片，直观上修复质量略优于BSCB算法和TV算法，而且从表1中可以看出其修复速度较前两种方法有很大的提高。

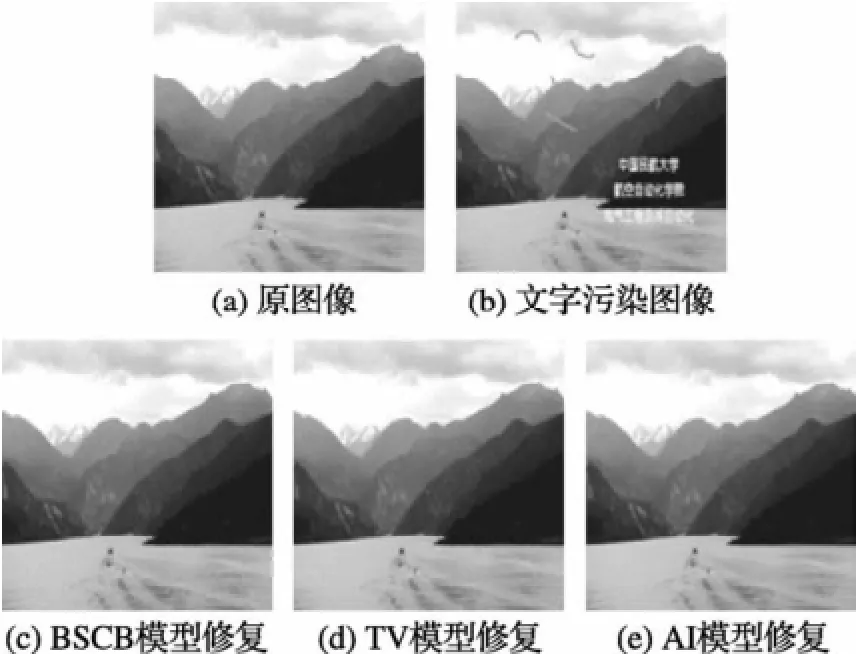
图4 Canyon图像去除文字效果比较

图4是用3种方法进行彩色图像canyon上文字去除的对比试验。虽然视觉效果没有太大差别，但是从表1和表2中可以看出新提出的AI方法时效比BSCB算法提高到2.5倍，比TV方法也稍有提高，而客观评价指标PSNR也比其它两种算法有明显提高。

实验过程中3种方法的运算时间和峰值信噪比比较如表1和表2所示。

表1 运算时间比较s

表2 峰值信噪比比较

5 结束语

本文把图像放大算法中插值的思想运用到图像修复中，提出了以基于扩散率函数的自适应插值算法。从仿真及计算PSNR的结果可以看出，该方法在保持图像修复质量基本不变的情况下，修复时效约为BSCB算法的4.8倍，而PSNR值比TV算法提高了许多。解决了传统的修复算法耗时长、效率低的问题。经过仿真结果表明，本文的方法修复后的图像信息过渡自然，视觉效果有很大提高，具有较强的实用价值。该算法均能得到比其它算法更好的效果。

［1］ Li X D，Du Y，Ling F.Using a subpixelmappingmodel to improve the accuracy of landscape pattern indices［J］.Ecological Indicators，2011，11（5）：1160－1170.

［2］ 张红英.数字图像修复技术的研究与应用［D］.成都：电子科技大学，2006.

［3］ Criminisi A，Perez P，Toyama K.Objectremoval by exemplarbased inpainting［C］／／Computer Vision and Pattern Recognition.USA：IEEE Computer Society Conference，2003：721－728.

［4］ Shen ZQ，Qi J G，Wang K.Modification of pixelswapping algorithm with initialization from a sub-pixel spatial attractionmodel［J］.Photogrammetric Engineering and Remote Sensing，2009，75（5）：557－567.

［5］ 许威威，潘志庚，张明敏.一种基于整体变分的图像修补算法［J］.中国图象图形学报，2002，7（4）：351－355.

［6］ 江雯，陈更生，杨帆.基于Sobel算子的自适应图像缩放算法［J］.计算机工程，2010，36（7）：214－216.

［7］ Hwang JW，Lee H S.Adaptive Image Interpolation Based on Local Gradient Features［J］.IEEE Signal Processing Letters，2004，11（3）：359－362.

［8］ 许微.基于偏微分方程的图像修复及放大算法研究［D］.天津大学，2007.

［9］ Perona P，Malik J.Scale-space and edge detection using anisotropic diffusion［J］.IEEE Trans on Pattern Analysis and Machine Intelligence，1990，12（7）：629－639.

［10］ Lin S Y，Shi J Y.Fast natural image matting in perceptual color space［J］.Computers and Graphics，2005，29（3）：403－414.

Application Research on Adaptive Interpolation Algorithm in Im age Restoration

MA Min1， ZHAO Liang1， WANG Hua-xiang2
（1.Civil Aviation University of China，Tianjin 300300，China；2.Tianjin University，Tianjin 300072，China）

Since the BSCBmodelhasan inherentslow rate，and the totalvariationmodel is subject to staircase effect，to overcome these disadvantages，an adaptive interpolation algorithm is proposed based on the diffusivity function.The proposed algorithm repairs the unknown pixels by using the gradient weight function and distance weight function of the neighboring pixels whose values are known.Experimental results show that compared to the traditional methods，the proposed algorithm can obtain relatively higher image quality in a shorter time for both gray and color image restoration，additionally，the quantitative evaluation indicator has also verified the effectiveness of the proposed method.

Metrology；Image restoration；Partial differential equation；Diffusivity function；Adaptive interpolation

TB96

A

1000-1158（2014）04-0331-04

10．3969／j．issn．1000-1158．2014．04．06

2012-07-18；

2013-05-28

国家自然科学基金青年基金（61102096）

马敏（1971－），女，安徽霍邱人，中国民航大学教授，研究生导师，主要从事无损检测及新型传感器的研究。mm5739＠163.com