电磁层析成像中新型归一化算法的设计与实现

李 柳， 邵富群， 王占军

（1.沈阳师范大学物理科学与技术学院，辽宁沈阳 110034；2.东北大学信息科学与工程学院，辽宁沈阳 110004；

3.沈阳师范大学计算机与数学基础教学部，辽宁沈阳 110034）

电磁层析成像中新型归一化算法的设计与实现

李 柳1， 邵富群2， 王占军3

（1.沈阳师范大学物理科学与技术学院，辽宁沈阳 110034；2.东北大学信息科学与工程学院，辽宁沈阳 110004；

3.沈阳师范大学计算机与数学基础教学部，辽宁沈阳 110034）

基于电容和电阻层析成像技术中灵敏度矩阵非线性归一化方法，提出了电磁层析成像中使用线性归一化方法的不合理性，在推导出其解析解的前提下，建立了电磁层析成像技术中的新型归一化模型，并给出了新型灵敏度模型的归一化公式。比较了原始和新型模型对于灵敏度归一化的效果，并将新型归一化模型应用到图像重建中，比较了成像质量，用相关系数比较了两种模型和原图的相关度，得出了结论：新型灵敏度归一化模型更逼近原始灵敏度的变化趋势，采用新型模型重建图像的质量更高。

计量学；电磁层析成像技术；归一化；灵敏度；图像重建

1 引 言

归一化是一种无量纲处理手段，使物理系统数值的绝对值变成某种相对值关系，是简化计算、缩小量值的有效办法。在电层析成像技术中存在不同的变量，例如检测电压、图像灰度、灵敏度等；也存在用同一单位表示同一变量的主成分数值大小差距比较大的现象，这样会出现“大数吃小数”的问题，将会忽略方差小的变量信息，倾向于方差大的变量信息。为了可以均等地对待每个变量，消除因单位和数值差距较大带来的影响，在使用数据前需要对原始数据进行归一化预处理。常见的归一化方法有线性函数转换法、对数函数转换法和反正切函数转换法。

图像重建是正向模型的逆问题，是严重病态逆问题，对检测值中的噪声非常敏感，微小的扰动会导致介质电导率或磁导率分布（由图像灰度向量表示）急剧变化，以至不能得到稳定的解。测量值或者灵敏度（物场中微小单元对检测值的影响程度）的归一化处理有助于降低噪声的影响。一般情况下，不同测量极板测得的测量值相差较大（通常相差几十甚至上百倍），而采用无量纲化的处理方法，即对测量值变化量和灵敏度矩阵进行归一化处理，通常可减少各电极对间电容值和噪声干扰。

2 电层析成像技术中的灵敏度归一化方法

对于电层析成像技术而言，从正问题的数学模型可以看出，测量值和灵敏度模型比较复杂，很难用解析方法求解，常用数值方法分析。因此，很难用上述归一化模型预处理数据，而要根据数学模型推导出特定的归一化模型。

对于电容层析成像技术（ECT）［1，2］，测量值和灵敏度归一化模型的选择依据相应的应用工艺场合及两相流的模型［3，4］。ECT技术通用的归一化模型主要有并联模型、串联模型、混合模型和Maxwell模型。对于不同类型的不同多相流模型，可以采用不同的归一化模型，即使采用同样的图像重建算法，成像质量也有很大差别。Yang对几种模型进行了对比研究，指出采用串联模型在大多数流型分布时，可以改善图像重建质量，更适合测量值与电容或等效介电常数为严重非线性的情况［5］。电阻抗层析成像技术（ERT）采用对数形式近似表示灵敏度归一化形式。

电磁层析成像技术（EMT）是能重现两种不同介电常数或磁导率物体分布的技术，它的正问题主要是研究检测线圈对传感器磁矢位的变化，逆问题是重建磁导率分布情况，即，利用测量的磁矢位实现图像重建。EMT系统主要重建不同磁导率两相流或多相流物场。为了提高重建图像的质量，一般情况下，都要对测量的磁矢位和灵敏度矩阵做归一化处理。传统的归一化方法是在假设EMT系统数学模型线性化前提下得到的，归一化的磁矢位满足线性归一化函数，即

式中，λold为一对线圈间的归一化磁矢位，Am为实际测量值，而Ah和Al为满场和空场时同一对线圈间的磁矢位测量值。从式（1）看，当物场中充满低磁导率媒质时，归一化磁矢位应该为0，当物场中充满高磁导率媒质时，归一化磁矢位为1，当物场中放置一个高磁导率物体时，归一化λold为Ah和Al之间的线性插值。

然而，实际的磁矢位A和磁导率的分布之间有很复杂的关系，

从式（2）看，磁矢位和磁导率不是简单的线性关系，因此，归一化磁矢位也不能套用传统的线性公式，要想得到归一化磁矢位公式，必须从式（2）的解析解出发推导出磁矢位和磁导率的关系。

3 电磁层析成像中归一化模型的建立

3.1 EM T中新型归一化模型的推导

对于二维平面场，A只有此平面的垂直分量，式（2）可简化成标量方程为

式（7）的通解为

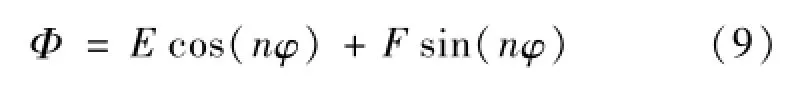
式（8）为虚宗量贝塞尔方程，它的解为

因此，可以得到式（5）的通解为

式中，A、B、E、F为常数。

利用分离变量法可以解出式（6）的通解为

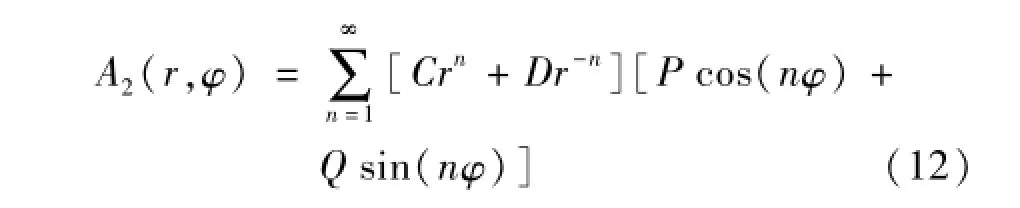
式中，C、D、P、Q为常数。

边界条件为：

（1）在物体和媒质分界面上A连续：

A1（a，φ）＝A2（a，φ）

（2）在物体和媒质分界面上H的切向分量相等，

由此可见，EMT的磁矢表达式不是线性形式，得到的归一化表达式也不能是线性的。如式（18）可知，归一化参数与满场和空场磁矢有关，是在传统参数的基础上添加了新的系数构成的，即

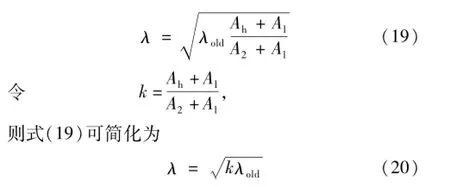
式中，k为修正参数。

3.2 EMT中不同归一化模型仿真结果分析

对于8线圈单激励EMT仿真系统，利用有限元法［7］解正问题得到检测值的数值结果，建立灵敏度矩阵，并利用不同的归一化方法（根据式（1）和式（20）的相应归一化处理方法分别称为“原始归一化方法”和“新型归一化方法”）对灵敏度进行预处理。

不同灵敏度归一化方法处理数据的结果如图1所示，比较了两种归一化方法对不同位置灵敏度的影响。图1（a）描述了物场中心处70个剖分单元的归一化灵敏度的分布情况，图1（b）描述了物场边缘处最外侧的70个剖分单元灵敏度受两种归一化处理方法的影响结果，其中，浅色实心圆圈表示按照式（20）计算所得的新型灵敏度归一化分布情况，深色空心圆圈表示按式（1）计算所得的原始归一化结果。从两种归一化结果可以看出：

（1）灵敏度新型归一化算法所得数据和线性归一化模型所得数据变化规律类似，但比较集中，符合实际灵敏度分布情况。

（2）中心处的单元灵敏度集中程度更高，集中在0.3～0.8之间，这样会在图像重建中提高图像的相关度。

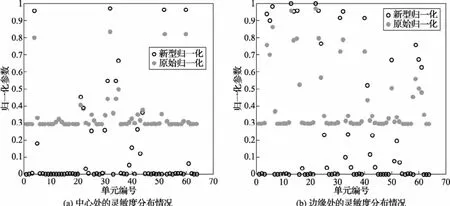
图1 不同灵敏度归一化算法的比较结果

通过标准Tikhonov正则化［8］方法和Landweber迭代法［9］对不同流型（如图2的（a）、（b）、（c）3种原型）进行图像重建。采用相关系数［10］评价图像质量，相关系数指标反映了原象与重建图像的像素灰度之间的相关性，列于表1。为了更好地比较4种归一化模型对成像质量的影响，最后灰度图像不进行灰度门限过滤处理。

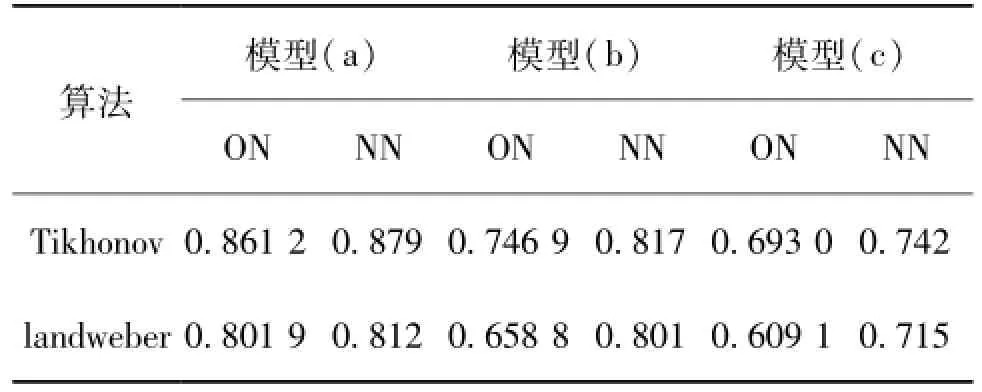
表1 新型和原始灵敏度归一化方法重建图像相关性比较

从图像重建结果和图像评价指标可以看出：新型灵敏度归一化算法的图像成像误差比原始算法小，相关性比较高，尤其对提高物场中心处的灵敏度起重要作用，使物场中心处物体的成像误差大大减小，更接近原始图像。

4 结 论

电磁层析成像技术中的新型灵敏度归一化模型是建立在其数值解的基础上的，和线性归一化模型相比，新型归一化模型的灵敏度分布更符合原始灵敏度的分布规律。用新型灵敏度归一化模型进行图像重建，采用相关度指标评价成像结果得出结论：新型灵敏度归一化算法的图像成像误差比线性算法小，相关性比较高，图像的相关度较高。

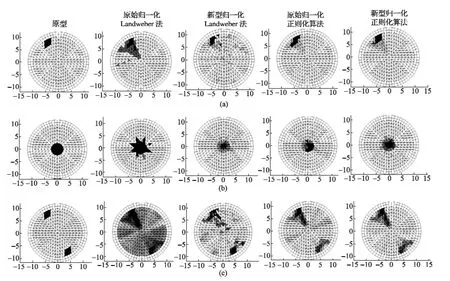
图2 新型和原始灵敏度归一化算法对成像结果影响

［1］ 马敏，王化祥，张炜宇.数字化电容层析成像系统［J］.计量学报，2007，28（3）：253－256.

［2］ 陆耿，彭黎辉，姚丹亚，等.电容层析成像系统的实用化设计［J］.计量学报，2004，25（3）：241－243.

［3］ Yang W Q，Chondronasios A，Nattrass S，etal. Adaptive calibration of a capacitance tomography system for imaging water drop let distribution［J］.Flow MeasurementandInstrumentation，2004，15（5－6）：249－258.

［4］ Yang W Q.An improved normalization approach for electrical［C］／／1 stWorld Congress on Industrial Process Tomography，Buxton，Great Manchester，1999.215－218.

［5］ 李柳，邵富群.电磁层析成像图像重建中的修正共轭梯度算法［J］.仪器仪表学报，2010，31（3）：655－658.

［6］ 熊汉亮，董琰婷，王安文，等.电磁层析成像技术的物理机制与检测极限［J］.天津大学学报，1998，31（2）：136－142.

［7］ Ma X，Peyton A J，Higson S R，etal.Hardware and software design for an electromagnetic induction tomography（EMT）system for high contrast metal process applications［J］.MeasurementScienceand Technology，2006，17（1）：111－118.

［8］ Scharfetter H，Kostinger A，Issa S.Hardware for quasisingle-shotmultifrequencymagnetic induction tomography（MIT）：the Graz Mk2 system［J］.Physiological Measurement，2008，29（6）：S431－S443.

［9］ Vauhkonen M，Hamsch M，Igney C H.A measurement system and image reconstruction in magnetic induction tomography［J］.PhysiologicalMeasurement，2008，29（6）：S445－S454.

［10］ 彭黎辉，陆耿，杨五强.电容成像图像重建算法原理与评价［J］.清华大学学报（自然科学版），2004，44（4）：478－484.

The Design and Realization of a New Normalization Algorithm in Electromagnetic Tomography

LILiu1， SHAO Fu-qun2， WANG Zhan-jun3
（1.College of Physics Science and Technology，Shenyang Normal Univerisity，Shenyang，Liaoning 110034，China；
2.College of Information Science and Engineering，Northeastern University，Shenyang，Liaoning 110004，China；
3.Shenyang Normal University，Shenyang，Liaoning 110034，China）

According to new sensitivity normalizations of electrical impedance and electrical capacitance tomography，the irrationality of linear normalization of sensitivity matrix of electromagnetic tomography is proposed.The new sensitivity normalizationmodel is established based on the analytical formula in electromagnetic tomography.The formula of the new sensitivity normalization is given.The normalization effect of new model is compared with the original.The new sensitivity normalization is applied to the image reconstruction，and evaluated the image quality using the criterion correlation.It is conclusion that the new sensitivity normalizationmodel ismore close to the original trend and got higher reconstruction image quality.

Metrology；Electromagnetic tomography；Normalization；Sensitivity；Image reconstruction

TB973

A

1000-1158（2014）01-0049-05

10．3969／j．issn．1000-1158．2014．01．11

2012-07-06；

2012-11-17

辽宁省自然科学基金（20102203）

李柳（1978－），女，辽宁沈阳人，博士，沈阳师范大学副教授，主要从事层析成像技术的研究。synuliliu＠sohu.com