层次分析法在学生评教中的应用

蒋和平

（黄山学院 数学与统计学院，安徽 黄山 245041）

1 引 言

层次分析法是70年代美国运筹学家T.L.Satty提出的一种定性和定量相结合的多目标决策分析方法。其基本原理是将要评价的系统的有关替代方案的各种要素分解成若干层次，并以同一层次的各种要素的权重，根据综合权重按最大权重原则确定最优方案。层次分析法是一种十分有效的系统分析方法，在经济管理，能源开发规划，水资源分析，交通运输，人才培养与就业预测等方面有广泛的应用[1-4]。由于在考虑分析时对数据的处理我们采用了Matlab软件会更加方便与有效。

2 层次分析法的步骤

在运用层次分析法解决问题的过程中，主要分成下面的4个步骤。

2.1 建立层次分析结构模型

深入分析实际问题，将有关因素自上而下分层（目标—准则或指标—方案或对象），上层受下层影响，而层内各因素基本上相对独立。

2.2 构造成对比较阵

用成对比较法和1-9尺度，构造各层对上一层每一因素的成对比较阵。

2.3 计算权向量并作一致性检验

对每一成对比较阵计算最大特征根和特征向量，作一致性检验，若通过，则特征向量为权向量。

2.4 计算组合权向量（作组合一致性检验）

组合权向量可作为决策的定量依据。

3 提出问题

随着大学教育的扩招，大学课程教学班的人数日益增加，为了提高教学质量，每个学校的教务处都开通学生评教系统，通过学生对教师的教学质量的评价，来对教师的日常教学进行监督和促进，进而提高教师的教学水平和课堂管理水平，达到教学相长的目的。但是影响学生评教的因素很多，主要考虑以下5个方面：

1.教学基本功； 2.教学方法与方式；

3.教学态度； 4.教学理念；

5.教学效果。

问题：假设有 A、B、C、D、E5 位任课老师被某个学生评价，从中选出一个最好的，因此他将选择和决策，问题是他将如何做出决策和选择呢？

4 层次分析法在学生评教体系问题中的应用

4.1 建立递阶层次结构模型

根据某位学生的个人情况，建立目标为学生评教的递阶层次结构模型，如图1。

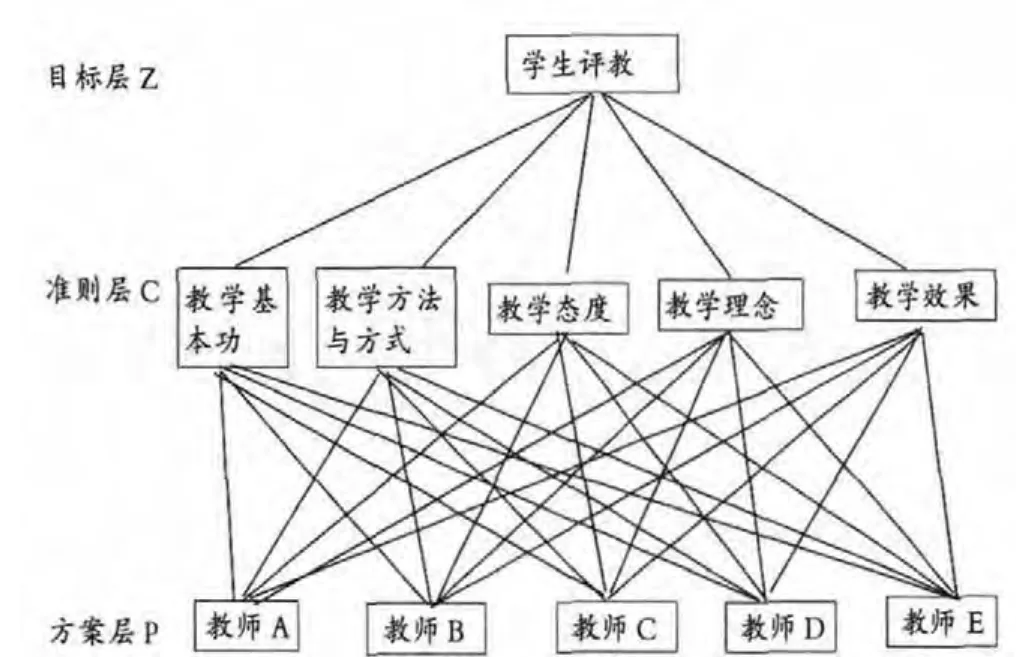
图1 递阶层次结构的模型

以上各层次之间的支配关系是完全的，那上一层次的每个元素均支配下一层次的所有元素。

4.2 构造成对比较阵，计算权重和一致性检验

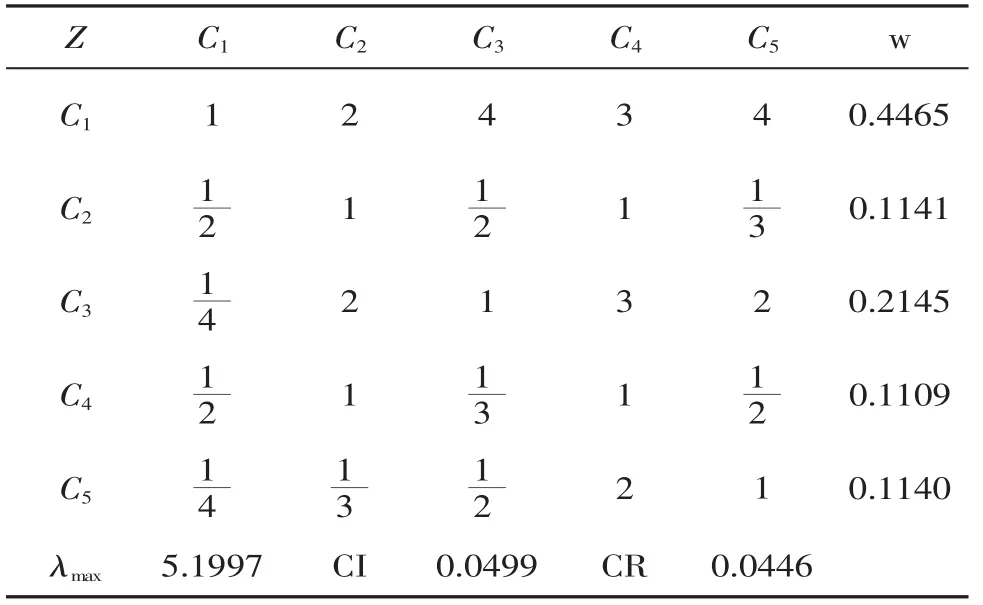
成对比较阵Z-C

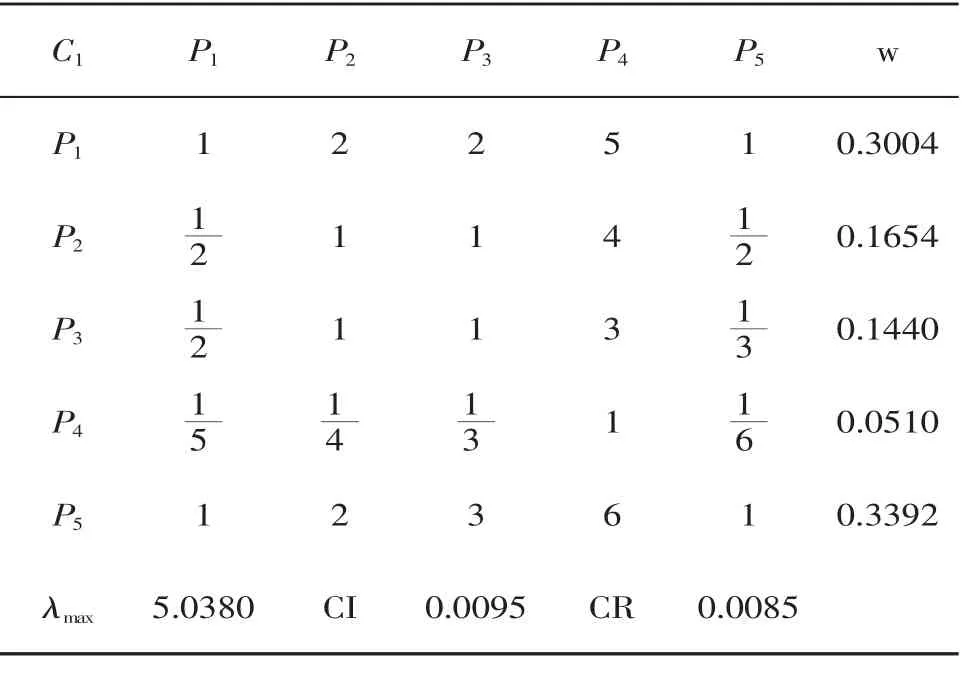
成对比较阵C1-P

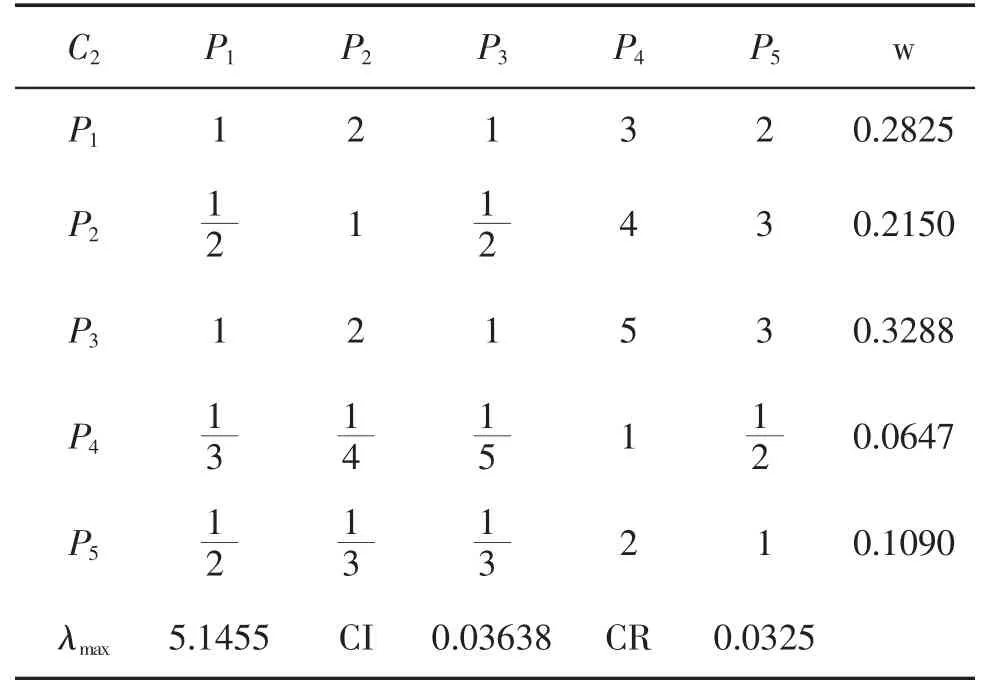
成对比较阵C2-P

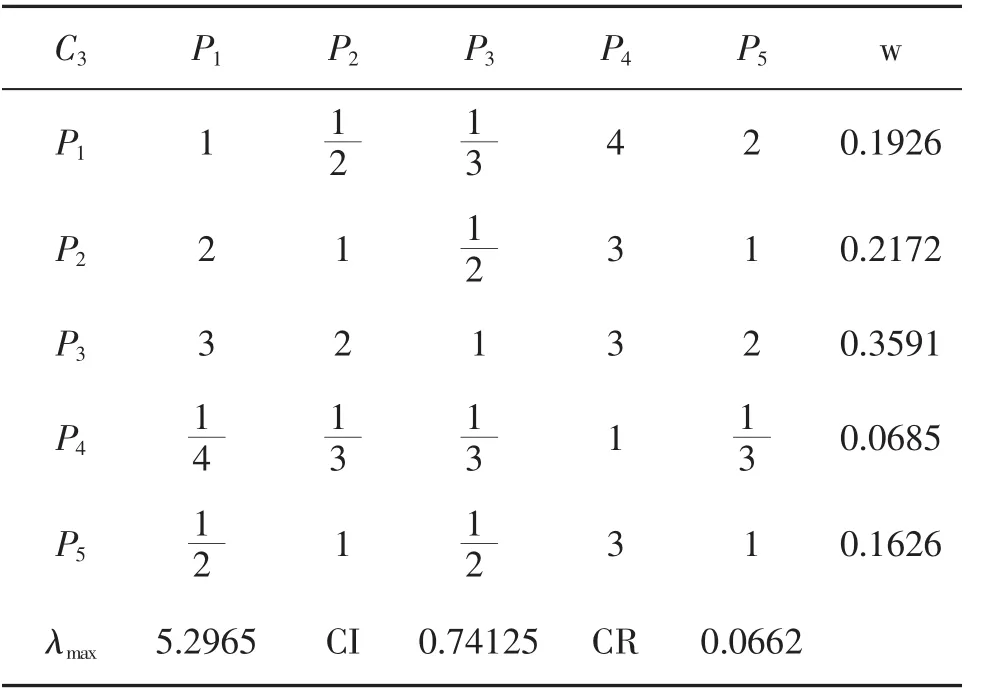
成对比较阵C3-P

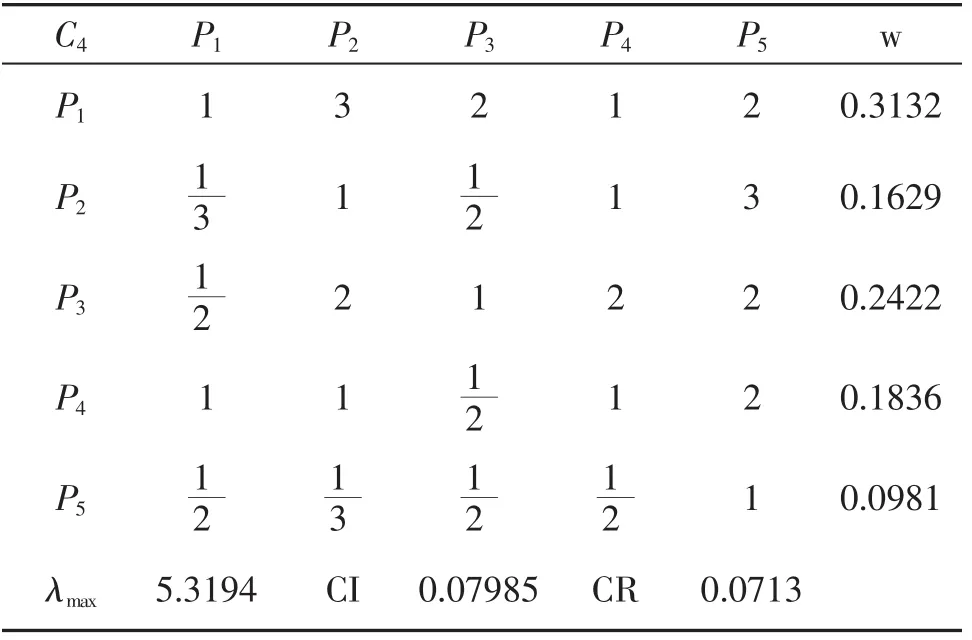
成对比较阵C4-P

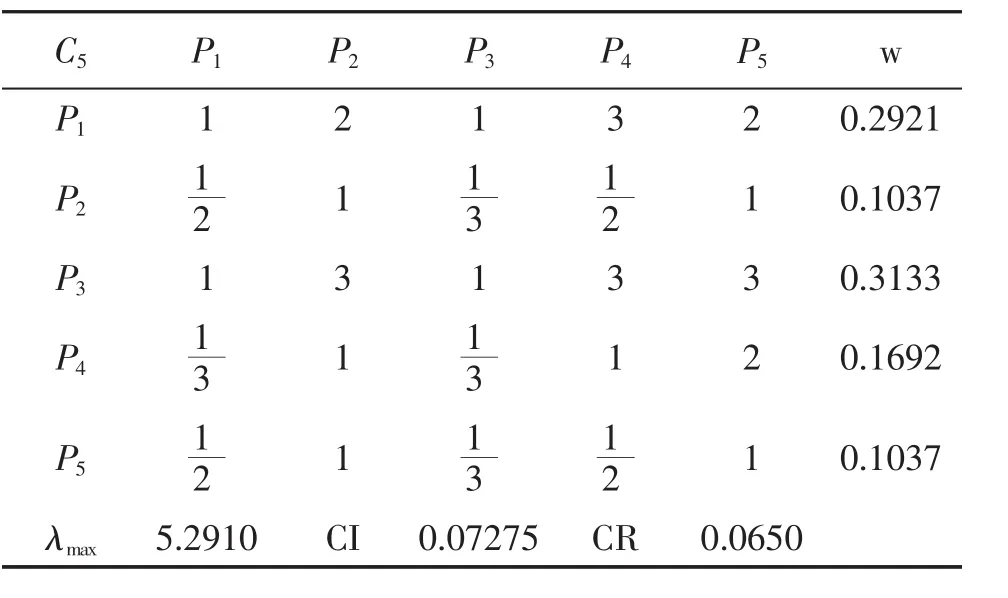
成对比较阵C5-P

4.3 层次总排序

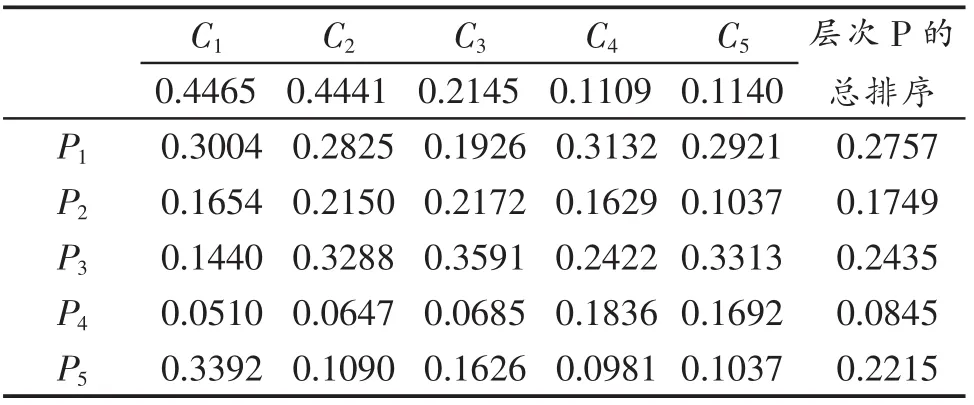
0.4465 0.4441 0.2145 0.1109 0.1140 P1 0.3004 0.2825 0.1926 0.3132 0.2921 0.2757 P2 0.1654 0.2150 0.2172 0.1629 0.1037 0.1749 C1 C2 C3 C4 C5 层次P的总排序P3 0.1440 0.3288 0.3591 0.2422 0.3313 0.2435 P4 0.0510 0.0647 0.0685 0.1836 0.1692 0.0845 P5 0.3392 0.1090 0.1626 0.0981 0.1037 0.2215

4.4 结果分析

由上述讨论知，A、B、C、D、E5 位老师所占权重的大小为：P1＞P3＞P5＞P2＞P4，即该生进行评教时，综合考虑得到教师A学生评教结果最好。教师D的学生评教结果最差，需要进行培训提高教学水平。

5 小 结

在该文中主要运用层次分析法结合Matlab软件解决了某位学生对5位教师的综合评价，是数学问题在实际问题中的很好运用。但是在设置比较判别矩阵时学生会被主观意识影响，所以采用多位学生的判断结果，会使结论更加客观些。

[1]唐耀平，陈幼林.层次分析法在高校毕业生择业中的应用[J].零陵学院学报，2004,（6）：191-193.

[2]肖磊，胡松.层次分析法在大学毕业生择业问题中的应用[J].教育时空,2005,（4）：80-83.

[3]姜启源，谢金星，叶俊.数学建模[M].北京：高等教育出版社，2003：242-243.

[4]杨桂元，黄己立，等.数学建模[M].合肥：中国科学技术大学出版社，2008：179-202.

[5]王琦，徐式蕴,等.MATLAB基础与应用实例集粹[M].北京：人民邮电出版社，2007：19-34.