千分表法测定金属丝的杨氏模量
2014-06-07黄秋萍
黄秋萍
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
千分表法测定金属丝的杨氏模量
黄秋萍
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
针对传统的拉伸法测定金属丝杨氏模量实验中涉及仪器多、待测物理量多以及实验调节繁琐等问题,设计了一种用千分表测定金属丝杨氏模量的实验装置,该装置用千分表直接测量金属丝因受外力而发生的微小形变量,再通过计算获得杨氏模量值。用该方法测定金属丝的杨氏模量大大降低设备要求,简化测量和计算,降低实验的系统误差。
杨氏模量;千分表;微小形变量;光杠杆
杨氏模量是表征固体材料性质的一个重要物理量,是工程技术中机械构件选材时的重要参数[1]。测定金属丝的杨氏模量实验的关键在于如何测量出金属丝因受外力而发生的微小形变,很多教材采用光杠杆放大法进行测量[2]。用光杠杆和望远镜标尺组合测量微小形变量的方法由于涉及的仪器较多,需要测量的物理量也较多,引入的误差相对较大[3_4],在测量过程中,望远镜和光杠杆的调节经常需要花费大量的时间。针对这些问题,为简化实验过程,提高实验测量的速度和精度,我们探索设计新的测量金属丝杨氏模量的实验装置:用千分表代替光杠杆来直接测量金属丝因受外力而发生的微小形变量,使实验过程操作简单、读数直观。
1 实验原理
一般实验教材中都有介绍拉伸法测金属丝杨氏模量的实验。在弹性限度内,长为L、横截面为S的金属丝,受到沿长度方向的外力F作用,金属丝的伸长量为ΔL,则金属丝单位面积上受到的垂直作用力为F/S(应力),金属丝的相对伸长量为ΔL/L(应变),根据胡克定律,应力与应变成正比,即


由式(2)可知,对于长度L、直径d及外力F均相同的情况下,杨氏模量E值大的金属丝伸长量ΔL较小,反之则越大。杨氏模量E值反映了材料抵抗外力产生拉伸形变的能力。由于金属丝的伸长量ΔL较小不易测量,所以拉伸法测定金属丝的杨氏模量值都是围绕如何测量金属丝的微小形变量ΔL而设计的[5_6]。
本文探索用千分表来直接测量金属丝因受外力而产生的微小形变量ΔL,实验装置如图1所示。该装置基本部件有金属丝的固定装置、滑轮、千分表、千分表的固定装置及砝码。由于金属丝需通过千分表,所以须对千分表进行一定的改装。将千分表的防尘帽及测头去掉,打开千分表的后盖,用塑料杆代替固有的金属杆做成千分表的升降量杆,将金属丝穿过千分表的升降量杆,调千分表的针位稳、准后才可使用。整个装置直接摆放在实验桌上,金属丝的固定装置可由铸铁材料做成,重心相对要低,防止翻倒。被测的金属丝左端连接在固定装置上,右端通过滑轮及千分表连接在金属丝夹上,金属丝夹下通过砝码盘挂上砝码,并将千分表固定在表夹装置上,调整砝码盘下砝码的数量,使千分表有一定的读数,当增加或减少砝码Δm时,千分表的读数变化量即为金属丝的伸长量ΔL,所以杨氏模量的计算公式即为
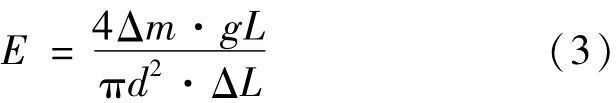

图1 千分表法测杨氏模量实验装置
2 实验数据记录与处理
实验中用最小分度1 mm的卷尺测量金属丝的长度L,具体数据如表1所示。用最小分度0.01 mm的千分尺测量金属丝的直径d,千分尺在金属丝的上、中、下三个部位的垂直方向上各测一次金属丝的直径d,具体数据如表2所示。为保证测量数据的准确性,我们在砝码盘上放置一定的砝码(3个200 g的砝码),使千分表有一定的读数(千分表的小指针指向0.2~0.4 mm之间),反复读取加减砝码(Δm=200 g)前后千分表的读数,千分表的读数变化量即为金属丝的伸长量ΔL,具体数据如表3所示。

表1 用卷尺测量金属丝的长度L mm
由表1可得,金属丝的长度L=598.1 mm± 0.6 mm
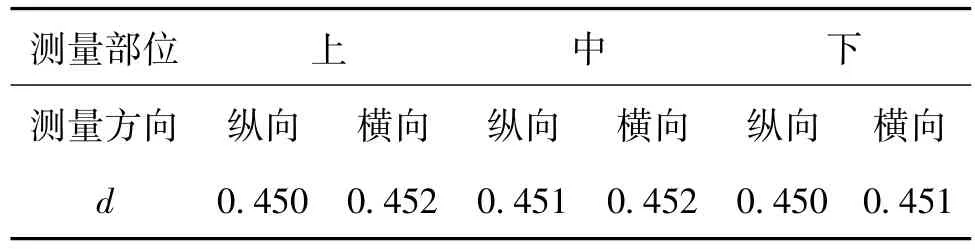
表2 用千分尺测量金属丝的直径d mm
由表2可得,金属丝的直径d=0.451 mm± 0.006 mm

表3 用千分表测量金属丝的伸长量ΔL mm
由表3可得金属丝的伸长量ΔL=0.036 0 mm ±0.000 6 mm
根据式(3)可得金属丝的杨氏模量值E=(2.04±0.06)×1011(N·m_2),符合公认值(金属丝杨氏模量的公认值为(2.01~2.16)×1011(N·m_2),且杨氏模量值E的不确定度较小,说明实验结果较为可靠。
3 结束语
从以上的测量过程和结果可以看出:测定金属丝的杨氏模量实验中,千分表法比传统的光杠杆放大法大大简化了实验装置,减少了待测物理量,降低了实验的系统误差,提高了测量的精度,同时,由于整个测量过程操作简单,易被学生接受和掌握;另一方面,由于涉及的仪器减少,有效降低实验成本,节约实验空间,提高实验室的利用率。
[1]方广利.大学物理实验[M].上海:同济大学出版社,2006:29_30.
[2]杨述武.普通物理实验(一、力学及热学部分)[M].3版.北京:高等教育出版社,2000:88_91.
[3]林登清,王新春,沈佳旺,等.测定钢丝杨氏模量的实验方案研究[J].物理通报,2013(2):47_50.
[4]胡益丰,沈大华,祁秀春,等.用拉伸法测钢丝杨氏模量实验中的不确定度分析[J].广西物理,2007,28 (4):56_59.
[5]李凡生.微小形变量的几种测量方法讨论[J].南宁师范高等专科学校学报,2009,26(3):123_125.
[6]刘乔花,王宛菁,李熊.用千分表测量金属丝的弹性模量[J].大学物理实验,2012,25(4):81_83.
M easurement for Young,s M odulus of M etal W ires by Using Dial Indicator
HUANG Qiuping
(College of Mathematics,Physics and Information Engineering,Zhejiang Normal University,Jinhua 321004,China)
The conventional experiments for the Young'smodulus of ametalwire by stretchingmethod,suffers from the excessive involved instruments,redundant parameters to bemeasured and complicated adjustments.A novel technique formeasuring Young'smodulus of ametal wire was proposed,in which the tiny stretch of themetalwire induced by the loaded tension ismeasured directly using a dial indicator and then the Young'smodulus can be calculated.As a result,the involved equipments decreased and measurement and calculation become simplified,which will degrade the systematic errors in the experiments.
Young'smodulus;dial indicator;micro deformation;optical lever
O4_33
A
10.3969/j.issn.1672_4550.2014.01.002
2013_07_05
浙江省自然科学基金项目(LQ13A040005)。
黄秋萍(1981_),女,硕士,工程师,主要从事大学物理实验教学与研究工作。
