考虑来水的东江流域用水量脉冲响应

何艳虎,陈晓宏,林凯荣,银磊,吴孝情(1.中山大学水资源与环境研究中心,广东广州510275; 2.华南地区水循环和水安全广东普通高校重点实验室,广东广州510275)

考虑来水的东江流域用水量脉冲响应

何艳虎1,2,陈晓宏1,2,林凯荣1,2,银磊1,2,吴孝情1,2
(1.中山大学水资源与环境研究中心,广东广州510275; 2.华南地区水循环和水安全广东普通高校重点实验室,广东广州510275)

运用协整的方法研究广东省东江流域近30年来总用水量与各行业用水量及流域来水量的长期关系,并建立了向量自回归模型对行业用水量和来水量的关系进行脉冲响应分析和方差分解。结果表明,东江流域总用水量的波动主要归因于生产用水的冲击,其对总用水量的方差贡献率之和长期达到91%以上,总用水量对来水的冲击呈现微弱负向响应；第二产业用水对自身和除第一产业用水外的行业用水波动影响强大而持久,为显著的正向响应,远大于各行业用水相互间的冲击。

用水量；向量自回归模型；脉冲响应；方差分解；东江流域

在当前气候变化和人类活动的剧烈影响下,极端水文气象事件的日益频繁、天然降水的更加集中与经济社会快速发展带来的人类生产生活均匀性用水量越来越大、保证率越来越高之间的矛盾日益突出[1]。区域用水量受产业结构及各行业用水定额影响的同时,也受一定时期有限的来水量制约,因此,如何协调变化环境下一定时期区域来水量、用水量及其产生的排污量之间的关系,尤其是在当前用水总量控制的社会命题下,实现社会、经济和生态环境综合效果最佳,是区域快速经济社会发展中的水安全和水资源高效可持续利用亟待解决的问题。研究变化环境下区域各行业用水量之间的响应关系可为动态预测需水,探究一定时期区域用水系统演化规律,进而为基于用水总量控制与水资源高效利用的水资源优化配置提供必要的基础。国内外学者对各行业用水量之间动态响应关系的研究尚不多见,对用水量及其驱动因素的研究多集中于定性方面的分析,定量分析不够。目前有产业用水量间驱动效应分解[2]、地区用水结构演变及成因分析[3]、基于用水量指标完全分解模型的用水驱动因素分解[4]等研究,而对各行业用水量间的长期相互影响关系的研究则较少。基于此,笔者根据广东省东江流域1980—2012年各行业用水量和来水资料,首先对总用水量和各行业用水量及区域水资源量的平稳性进行检验,用协整的方法来研究它们的长期关系,建立向量自回归(vector autoregressive,VAR)模型,并在此基础上对各行业用水量及区域来水量间的相互关系进行脉冲响应分析和方差分解,定量分析它们之间的影响关系,探究来水量和水资源需求量之间的响应规律,为变化环境下流域用水的科学管理提供参考依据。

1 VAR模型介绍

VAR模型是一种非结构化的多方程模型,不需对模型中的变量是内生还是外生进行假定,也不需做任何先验性约束,基于此模型可以进行方差分解和脉冲响应分析,预测随机扰动对系统的动态冲击。在模型的每一个方程中内生变量对模型的全部内生变量的滞后值进行回归,从而估计全部内生变量的动态关系,避免了划分解释变量和被解释变量的主观随意性问题。鉴于模型上述特点及良好的性质,其在经济管理领域得到了广泛应用,在描述区域经济发展与产业结构调整[5]、对外直接投资和贸易[6]及劳动生产率和工资[7]等动态关系方面发挥了重要作用,近年来其适用性也得到进一步拓展[8-9]。

VAR模型的一般模型数学表达式为

式中：Yt为m维内生变量向量;Xt为d维外生变量向量;A1,…,AP和B1,…,Br为待估计的参数矩阵;下标P和r分别为内生变量和外生变量滞后期的阶数,一般根据赤池信息准则(Akaike information criteria,AIC)和施瓦兹准则(Schwarz criteria,SC)信息量取值最小的准则和似然比(LR)检验来确定;着t为随机扰动项,与同时刻的元素可以彼此相关。

通过VAR模型的估计,可检验各个变量是否能够解释其他变量的历史变化,进而利用基于VAR模型的脉冲响应函数和方差分解方法,测算模型中各方程随机扰动项的冲击对各变量的动态影响,并比较各方程新息对变量波动的重要性。在进行各变量VAR建模之前,必须对各时间序列的随机性和平稳性进行分析,如进行单位根检验,以判断它们是否满足建模条件,即自变量和因变量之间是否有长期稳定的均衡关系。一般可用协整的方法通过对回归系数的Johansen协整检验和回归残差的协整检验来研究各变量的长期均衡关系[7]。多变量的VAR建模分析流程如图1所示。

图1 多变量的VAR建模分析流程

本文通过构建研究区东江流域来水量和各行业用水量的VAR模型,对各变量脉冲响应函数和方差分解进行分析,对流域一定时期来水量和行业用水量间的动态响应关系进行实证研究。

2 行业用水量间动态关系分析

2.1 研究区概况

东江流域位于珠江流域东北端,流域平均年降雨量1795mm,汛期雨量占年雨量的83%左右,降水量充沛,时空变化大[10];东江是河源、惠州、东莞、广州、深圳以及香港3 000余万人口的生产、生活、生态用水水源。流域内和受水区经济普遍较为发达,受水区的地位特殊,尤其是对港供水的特殊性,使得东江供水安全具重大政治经济意义。流域多年平均径流量为326.6亿m3,现状供水能力超过100亿m3,设计供水能力约125亿m3。截至2012年底,河道外年取水总量已经超过90亿m3,总量上已十分接近流域分水总量的106.64亿m3,供用水强度大,现状用水量已接近饱和。

2.2 考虑来水的东江流域行业用水量间动态关系

选取广东省东江流域1980—2012年天然来水量和生产、生活和生态等各行业用水量数据为研究对象,并以此构建VAR模型。流域天然来水量为水文控制站博罗站天然流量序列,由广东省水文局提供;各行业用水量由历年《广东省水资源公报》及统计年鉴整理而得。

采用WZYS表示总用水量,WLS表示来水量,WYC, WEC,WSC,WSH,WST分别表示第一、二、三产业用水量,生活用水量和生态用水量。首先采用ADF (augmented dickey-fuller)单位根检验法对各时间序列的平稳性进行检验,判别其是否为平稳序列,以消除直接用经典的最小二乘法估计易出现伪回归现象的影响。各时间序列取对数后的ADF单位根检验结果如表1所示。这里各时间序列取对数是为了消除变量间的异方差性[7]。

表1 广东省东江流域各行业用水量和来水序列取对数后ADF单位根检验结果

由表1结果可见,第二、三产业用水量,生活用水量和生态用水量的原水平序列都是非平稳的,存在单位根,但一阶差分以后连同其余变量时间序列,都变成了平稳序列,达到了1%的显著性水平。直接建模而不加检验则可能出现“伪回归”现象。针对此问题,通过协整检验的方法来研究广东省东江流域各行业用水量和来水量之间的长期关系。影响总用水量的因素很多,且各影响因素间相互作用关系较复杂[7],为简要表征总用水量与各行业用水量、来水量之间的关系,只考虑流域各行业历史用水量和来水量。首先用最小二乘法进行回归估计,得到各时间序列的长期均衡关系式为

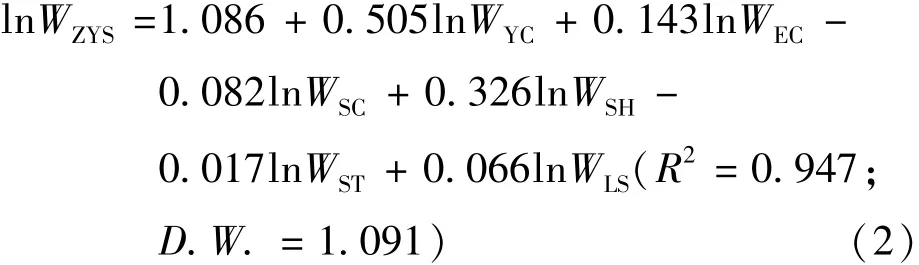
这里D.W.表示检验自相关的统计量。

式(2)右边各项t检验值分别为2.22,4.09, 1.91,-1.73,2.78,-0.36,1.86。为判断式(2)关系是否真实,运用ADF单位根检验法对其残差序列进行单位根检验,以检验其是否平稳,进而推测自变量和因变量之间的协整关系,若平稳,则说明因变量能被自变量的线性组合所解释,即自变量、因变量间存在协整关系。结果表明,ADF值-5.358在1%的显著性水平下小于临界值-4.309,残差为平稳序列,表明式(2)中自变量和因变量之间具有协整关系,即广东省东江流域总用水,第一、二、三产业用水,生活用水,生态用水和来水之间存在长期均衡关系。由于协整关系的存在,可以用其他变量的变化来影响另一个变量的变化。

广东省东江流域各行业用水量和来水量之间存在长期的均衡关系,彼此相互影响和制约,可建立向量自回归模型,并在此基础上用脉冲响应函数和方差分解来研究它们之间的动态响应关系。依据式(1),构建广东省东江流域各行业用水量和来水量的VAR模型,这里滞后期P取2。各方程的检验结果表明,除第一产业用水量和来水量,其余各变量的回归方程判定系数均达到90%以上,拟合效果较好,说明本文建立的VAR模型能较好地反映流域总用水,第一、二、三产业用水量,生活用水量,生态用水量和来水量之间的相互影响程度。

在建立的VAR模型基础上,通过脉冲响应函数来描述各行业用水和来水作为因变量,其他变量包括因变量自身滞后值1个标准差的随机扰动所产生的影响,以及其影响路径的变化过程。各行业用水量和来水量之间的脉冲响应函数合成如图2所示。

如图2所示,横轴表示冲击作用的滞后期间数,纵轴则表示各因变量的变化。由于各因变量均取对数,所以,图中纵轴数值代表弹性系数。

2.2.1 分析WYC分别对其他变量1个标准差新息扰动的响应路径

图2(a)显示WYC对自身的1个标准差新息立刻有较强的正向反应,呈下降趋势,第2到第4期反应明显,为负向响应,此后呈现出微弱而缓慢的上升趋势;来自WEC的1个标准差新息扰动影响呈波浪式变化,分别在第4期和第6期出现波峰和波谷,呈现显著的负向响应;来自WSC的1个标准差新息扰动在第2期反应明显,此后呈下降趋势,缓慢而微弱,在第8期之前为正向响应,之后为负向响应;来自WSH的1个标准差新息扰动在第4期之前为微弱的正向响应,之后为负向响应;来自WST和WZYS的1个标准差新息扰动忽高忽低,为正向响应;来自WLS的1个标准差新息扰动在第4期之前为明显的负向响应,第5期WYC增加了0.18,此后呈下降趋势。

2.2.2 分析WEC分别对其他变量1个标准差新息扰动的响应路径

图2(b)显示WEC对自身1个标准差新息有正向显著反应,在第1期WEC增加了0.3,此后平稳下降,至第10期仍大于0.2;来自WYC的1个标准差新息扰动呈负向显著反应,第3期WEC减少0.16,此后上升趋势明显,至第10期后呈现向零效应收敛的迹象;来自WSC的1个标准差新息扰动呈负向显著反应,但响应过程较为平稳;来自WZYS、WLS和WSH的1个标准差新息扰动响应路径相似,前期下降,后期缓慢上升,影响程度依次减弱;来自WST的1个标准差新息扰动在第4期之前为微弱的正向响应,此后呈零效应收敛。

2.2.3 分析WSC分别对其他变量1个标准差新息扰动的响应路径

图2(c)显示WSC对自身1个标准差新息扰动在前3期反应迅速,呈下降趋势,除第1期外,为负向响应,第6期后逐渐上升,至第10期收敛于零;来自WYC的1个标准差新息扰动表现为较为明显的负向响应,在第6期出现拐点;来自WEC的1个标准差新息扰动反应迅速,呈显著的正向响应,自第1期开始呈下降趋势,在第10期仍使WSC增加0.1;来自WZYS和WSH的1个标准差新息扰动路径相似,后者在第4期之前反应迅速,在第4期达到-0.08,此后呈上升趋势,至第10期收敛于零;来自生态用水的1个标准差新息扰动忽高忽低,为正向响应,在第5期后缓慢而微弱;来自WLS的1个标准差新息扰动呈波浪式发展,在第5期前后分别为微弱的正向和负向响应。

图2 各行业用水及WZYS和WLS对1个标准差新息扰动的响应路径

2.2.4 分析WSH分别对其他变量1个标准差新息扰动的响应路径

图2(d)显示WSH对自身1个标准差新息扰动缓慢而微弱,在第5期前后分别为正向和负向响应;来自WEC的1个标准差新息扰动忽高忽低,为十分显著的正向响应;而来自WYC的1个标准差新息扰动在第3期之前反应迅速,此后为缓慢的上升趋势,较为平稳,为显著的负向响应;来自WSC的1个标准差新息扰动在第4期之后反应迅速,第6期后趋于平稳,为显著负向响应;来自WST的1个标准差新息扰动在第3期前为微弱负向响应,此后趋于零收敛现象;来自WZYS和WLS的1个标准差新息扰动为波浪式路径,分别在第3期和第5期后为显著的负向响应。

2.2.5 分析WST分别对其他变量1个标准差新息扰动的响应路径

图2(e)显示WST对自身1个标准差新息扰动呈下降趋势,在第4期之前反应迅速,为正向响应,此后为平稳微弱的负向响应;来自WEC和WYC的1个标准差新息扰动分别呈明显的正向和负向响应;来自WSC和WSH的1个标准差新息扰动路径相似,在第4期之前反应迅速,负向响应明显,此后前者为缓慢下降趋势,后者响应微弱而收敛于零;来自WZYS和WLS的1个标准差新息扰动路径十分相似,在第2期后反应迅速,第6期后为显著的负向响应。

2.2.6 分析WLS分别对其他变量1个标准差新息扰动的响应路径

图2(f)显示WLS对自身1个标准差新息扰动在第5期之前为微弱的正向响应,之后为微弱的负向响应;除来自WSC的1个标准差新息扰动在第4～7期之间为显著负向响应外,其余变量的1个标准差新息扰动总体都较为微弱。

2.2.7 分析WZYS分别对其他变量1个标准差新息扰动的响应路径

图2(g)显示WZYS对自身1个标准差新息扰动在第4期之前反应迅速,之后为较为平稳的负向响应;来自WYC、WSC的1个标准差新息扰动在第3期之前反应十分迅速,之后为显著的负向响应;来自WEC的1个标准差新息扰动为显著的正向响应;来自WSH和WST的1个标准差新息扰动路径在第3期后几乎重叠,响应微弱而趋于零;来自WLS的1个标准差新息扰动呈波浪式路径,在第6期后为显著的负向响应。

可以看出,除WYC和WLS脉冲响应外,广东省东江流域WEC的1个标准差新息扰动对自身和行业用水的冲击作用显著,且均为正向响应,远大于行业用水对它的影响及行业用水相互间的影响。行业用水和WLS对WYC的1个标准差新息扰动呈显著的负向响应,WST对各行业用水及来水冲击作用微弱,WLS对各行业用水的冲击作用反应微弱。除WEC和WST外,行业用水间相互冲击作用在第4期后较为显著,多为负向响应。

脉冲响应函数描述的是VAR中的一个内生变量的冲击给其他内生变量所带来的影响。而方差分解是把内生变量中的变化分解为对VAR的分量冲击。因此,方差分解给出对VAR中的变量产生影响的每个随机扰动的相对重要性的信息。为进一步定量地分析广东省东江流域各行业用水量和来水量间的动态响应关系,通过方差分解给出各变量的冲击分量,各行业用水和来水的方差分解结果如表2～表8所示。

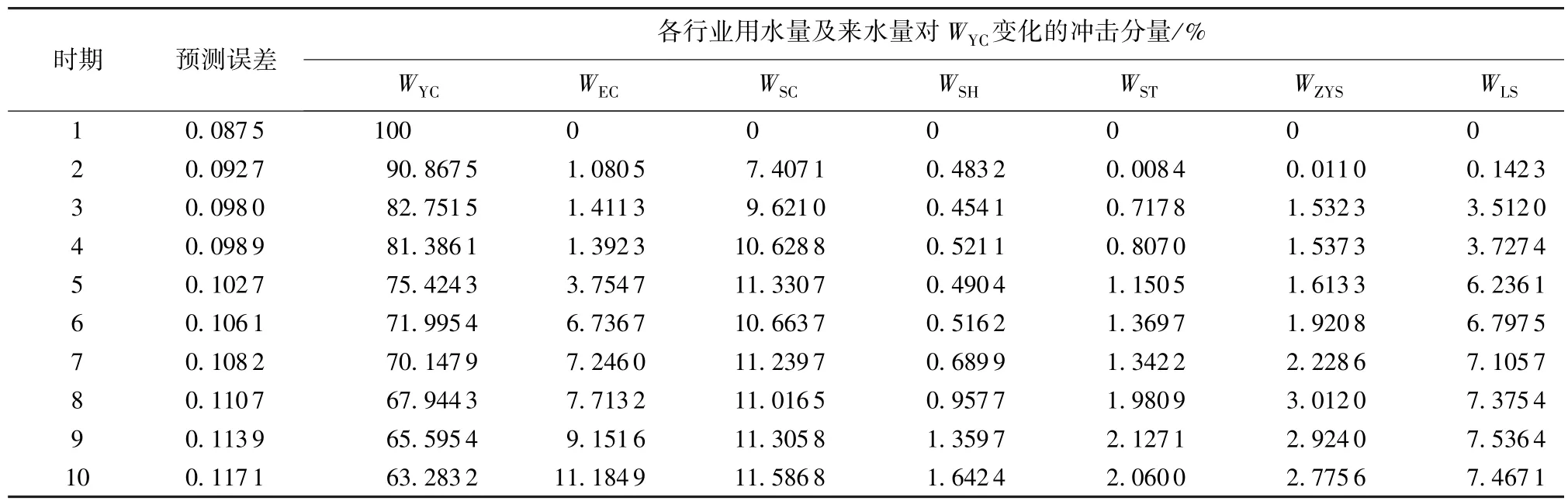
表2 第一产业用水的方差分解结果

从表2～8可以看出,广东省东江流域WYC的波动主要归因于其本身的冲击,自身冲击在第5期解释了产生波动的75%,第5期以后的解释作用也在63%以上;其次依次为WSC、WEC,并且随着时间的推移,它们的影响总体上越来越大,在第6期后均达到11%;其余行业用水的解释作用微弱。WEC的波动主要归因于其本身的冲击,第10期的解释作用仍在65%以上,其次依次为WYC、WSC,随着时间推移,WSC解释作用呈波动减少趋势,而WSC的波动主要由于WEC的冲击,第10期的解释作用达到58%,其本身的冲击次之,且与WYC的解释作用相当。WYC,WEC, WSC,WSH,WST这种影响程度呈波动变化;WST和WLS对WSC的解释作用微弱,在相当长的时间内不足5%。WSH的波动主要归因于WEC的冲击,最小时仍达到67%,其次为WYC的冲击,其解释作用逐渐增大,在第10期达到19%,WSC对WSH波动的影响随时间推移在增加,但未超过6%。WST的波动主要归因于生产用水的冲击,其中作用最明显的是WEC,各时期解释作用相差不大,但都超过66%,其次为WYC和WSC,前者影响随时间推移在缓慢增加,后者则呈减弱趋势。WZYS的波动主要由WEC、WYC、WSC解释,其

中WEC的解释作用最为明显,WSC的冲击作用超过了90%,解释作用最小的为WST,不足0.5%。WLS的波动主要归因于其本身的冲击,尽管其解释作用随时间推移逐渐减少,但在每一期其对自身波动的影响是最大的;其次为WSC,其对WLS的解释作用在第5期后显著增大,最高达到28%。WST和WZYS、WYC和WSH对WLS的冲击作用相当,但均未达到10%。

表3 第二产业用水的方差分解结果

表4 第三产业用水的方差分解结果

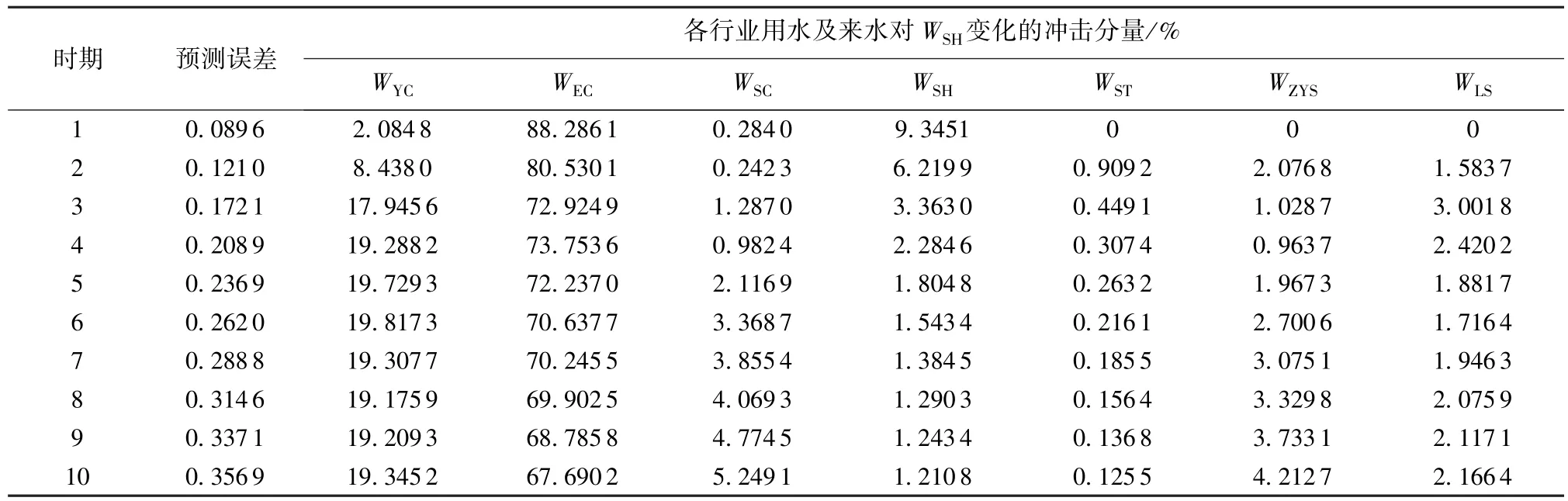
表5 生活用水的方差分解结果

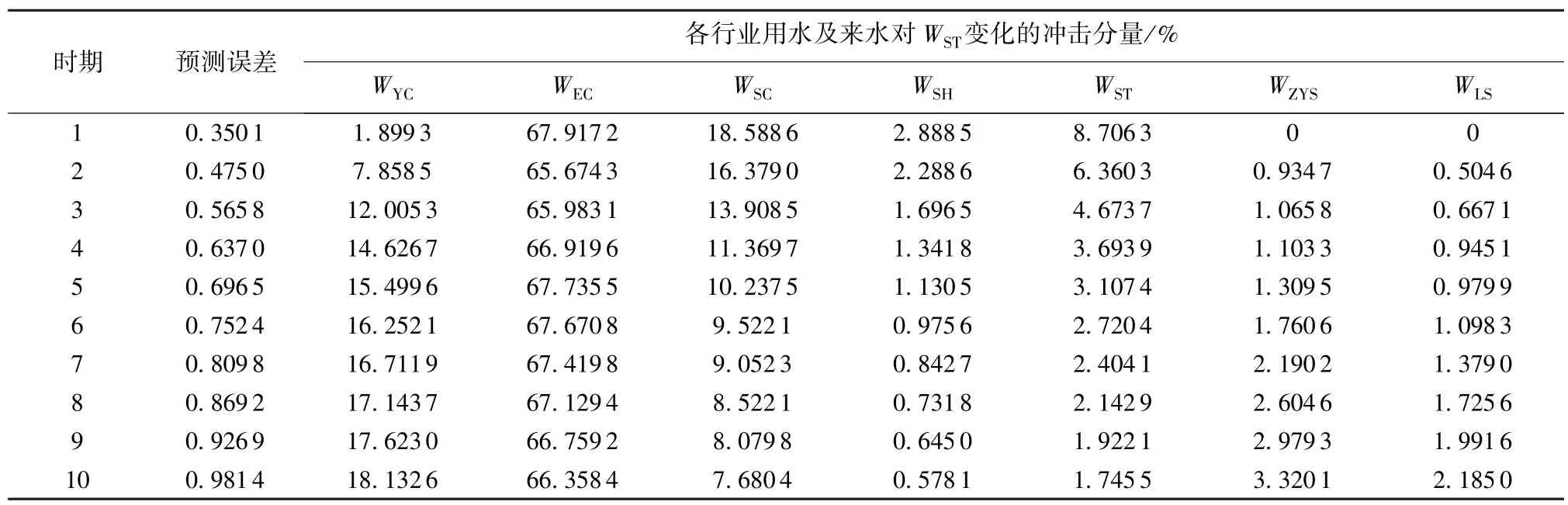
表6 生态用水的方差分解结果

从上述分析可知,就各行业用水的方差分解而言,除WYC外,WEC的冲击对WSC、WSH、WST和WZYS的波动具有相当大的解释作用,在较长时期内对它们的方差贡献率分别在58%、67%、65%和34%以上,说明它对行业用水的影响强度大且持久,远大于行业用水自身的解释能力及其相互间的冲击;WST对WLS波动的解释作用相较于其对行业用水波动的解释作用显著提高;WSC,对WZYS的方差贡献率之和长期达91%以上,对流域总的用水变化影响深远。

表7 总用水的方差分解结果

表8 来水的方差分解结果

3 结语

本文将广泛应用于数量经济领域中的向量自回归理论引入到流域行业用水相互作用关系的研究之中,建立了考虑来水的流域各行业用水量的VAR模型,通过脉冲响应和方差分解分析,揭示流域各行业用水和来水长期的动态响应关系,量化各行业用水和来水对总用水波动的解释作用,为变化环境下揭示流域用水演化规律提供了新的研究途径。

结果表明,近30年来,广东省东江流域第二产业用水量的1个标准差新息扰动对自身和行业用水量的冲击明显,表现为显著的正向响应,远大于行业用水对它的影响及行业用水量相互间的冲击,行业用水量和来水量对第一产业用水量的1个标准差新息扰动表现为显著的负向响应。第二产业用水量对第三产业用水量、生活用水量、生态用水量和总用水量波动的方差贡献率分别在58%、67%、65%和34%以上,生产用水量对流域总用水量的方差贡献率之和长期达91%以上,是引起总用水量波动的主要原因。针对当前用水总量控制的社会命题,在维持现状生活和生态用水状况的基础上,东江流域应通过提高工艺水平,加大节水力度,着重提高生产用水效率,尤其是提高第二产业用水效率,以达到用水总量有效控制的目的。

[1]TEEGAVARAPU R S V,GOLY A,OBEYSEKERA J. Influences of Atlantic multidecadal oscillation phases on spatial and temporal variability of regional precipitation extremes[J].Journal of Hydrology,2013,495：74-93.

[2]吕文慧,高志刚.新疆产业用水变化的驱动效应分解及时空分异[J].资源科学,2013,35(7)：1380-1387. (LYU Wenhui,GAO Zhigang.The driving effect and spatial-temporal differentiation of industrial water use in Xinjiang[J].Resource Science,2013,35(7)：1380-1387. (in Chinese))

[3]陈秀芬.基于信息熵的厦门市用水结构演变及其驱动力的灰色关联分析[J].水资源与水工程学报,2013,24 (2)：188-191.(CHEN Xiufen.The grey correlation analysis of the water structure evolution and its driving force in Xiamen based on information entropy[J].Journal ofWater Resource and Water Engineering,2013,24(2)：188-191.(in Chinese))

[4]佟金萍,马剑锋,刘高峰.基于完全分解模型的中国万元GDP用水量变动及因素分析[J].资源科学,2011 (10)：1870-1876.(TONG Jinping,MA Jianfeng,LIU Gaofeng.Analysis of China's ten thousand yuan GDP water consumption change and its factors based on the complete decomposition model[J].Resource Science, 2011(10)：1870-1876.(in Chinese))

[5]赵明,张蓉.江苏省对外直接投资与产业结构调整关系研究：基于VAR模型的实证分析[J].科技管理研究, 2013(4)：95-98.(ZHAO Ming,ZHANG Rong.Study on the relationship between the foreign direct investment and industrial structure adjustment in Jiangsu Province：empirical analysis based on VAR model[J].Science and Technology Management Research,2013(4)：95-98.(in Chinese))

[6]魏刚,谢臻.我国对外直接投资与对外贸易间的动态关系：基于VAR模型的实证分析[J].财经论丛,2009 (4)：8-14.(WEI Gang,XIE Zhen.The dynamic relationship between foreign direct investment and foreign trade in China：empirical analysis based on VAR model [J].Collected Essays on Finance and Economics,2009 (4)：8-14.(in Chinese))

[7]丁元.劳动生产率与工资关系的脉冲响应分析：以广东省为例[J].中国人口科学,2007(3)：72-80.(DING Yuan.The impulse response analysis of relationship between labour productivity and wage：a case study of Guangdong Province[J].Chinese Journal of Population Science,2007(3)：72-80.(in Chinese))

[8]PATILEA V,RAÏSSI H.Corrected portmanteau tests for VAR models with time-varying variance[J].Journal of Multivariate Analysis,2013,116：190-207.

[9]JARKKO P,JÄÄSKELÄD J.Monetary policy and the exchange rate：evaluation of VAR models[J].Journal of International Money and Finance,2011,30：1358-1374.

[10]陈晓宏,刘德地,刘丙军,等.湿润区变化环境下的水资源优化配置理论方法与东江流域应用实践[M].北京：中国水利水电出版社,2011.

Im pulse response of water consum ption in Dongjiang River Basin considering inflow

HE Yanhu1,2,CHEN Xiaohong1,2,LIN Kairong1,2,YIN Lei1,2,WU Xiaoqing1,2
(1.Center ofWater Resources and Environment Research,Sun Yat鄄Sen University,Guangzhou 510275,China; 2.Key Laboratory ofWater Cycle and Water Security in Southern China ofGuangdong Higher Education Institutes, Sun Yat鄄Sen University,Guangzhou 510275,China)

The cointegrationmethod was used to study the long-term relationships between totalwater consumption, industrial water consumption,and basin inflow over the past30 years in the Dongjiang River Basin,in Guangdong Province.The vector autoregressive(VAR)model was established for impulse response analysis and variance decomposition of the relationship between industrial water consumption and inflow.The results show that the fluctuation of total water consumption in the Dongjiang River Basin ismainly due to the impact of the production water,which accounts for over 91%of the variance contribution rate for a long time.The impact of the totalwater consumption on the basin inflow presents a slightly negative response.The secondary industrial water consumption has a significant and durable effect on itself and all other industrial water consumption except for the primary industry water consumption,showing a significantly positive response,which is much greater than the mutual impact ofwater consumption of various industries.

water consumption;vector autoregressive model;impulse response;variance decomposition; Dongjiang River Basin

TV213.4

A

1004 6933(2014)05 0044 08

2013 12 16编辑：高渭文)

10.3969/j.issn.1004 6933.2014.05.008

国家自然科学基金(51210013,51379223);水利部公益性行业科研专项(201301002-02)

何艳虎(1986—),男,博士研究生,研究方向为水文与水资源。E-mail：heyanhu456@163.com

陈晓宏,教授。E-mail：eescxh@mail.sysu.edu.cn