复杂河网引清流量优化分配模型
2014-06-07薛联青王思琪邢宝龙段小兰石河子大学水利建筑工程学院新疆石河子8009河海大学水文水资源学院江苏南京10098福州市规划设计研究院福建福州5000
薛联青,王思琪,邢宝龙,段小兰(1.石河子大学水利建筑工程学院,新疆石河子8009; .河海大学水文水资源学院,江苏南京10098;.福州市规划设计研究院,福建福州5000)
复杂河网引清流量优化分配模型
薛联青1,2,王思琪2,邢宝龙2,段小兰3
(1.石河子大学水利建筑工程学院,新疆石河子832009; 2.河海大学水文水资源学院,江苏南京210098;3.福州市规划设计研究院,福建福州350003)
根据物质守恒原理,建立复杂河网引清流量优化分配模型,以实现引清调度优化。鉴于模型中河段水质与流量的隐函数关系,利用罚函数法进一步优化模型的非线性约束,使河段水质目标呈隐式表达形式,达到减少决策变量与约束条件的目的。建立不同初始点为搜索起点,利用模式搜索法对优化模型进行求解。求解结果表明,不同初始点对求解结果影响明显。进一步分析河段污染物衰减的影响因素,并以参数形式表征水动力的影响,从而建立河段引清流量的修正模型。将修正模型应用到福州内河的引清流量计算中,计算结果表明,修正计算结果比试算法结果减少7.2m3/s,大大减少了引清流量,较好实现了引清流量的优化分配。
引清调度;流量分配模型;罚函数法;模式搜索法
随着经济的发展,城市内河中的污染物排放量加大,加上河道本身的水环境容量有限,导致内河污染物严重超标。为了改善内河水环境,采取了截污、引清调度等工程措施。引清调度以其能增加水环境容量、改善水动力条件,成为内河水环境治理中一种有效方法。但是,污染源与河网的空间分布特征条件使得不同的水流调控方式产生的水环境改善效果不同,因此,在确定水流调控方式之前,需要进行方案优选。目前,进行方案优选的方法有3类:①建立水动力水质耦合模型,对比几种可行调度方案的调度效果,选择一个较优的调度方案[1-2]。此种优选方法全局性较差,不能确定内河所需的最小引清流量,且方案设置具有盲目性,方案比选需要耗费大量人力,但该方法适用性较强,是目前引清调度方案优选方法中最常用的。②建立参数优选的智能算法与水动力水质模型耦合的优化模型[3-4]。该模型试图解决水质模型运行耗时大以及求解优化问题时存在大量迭代计算的缺陷。③建立水动力水质耦合模型,并结合神经网络拟合模型,采用耦合优化方法与神经网络模型进行方案优化[5-6]。神经网络模型对水动力模型的拟合效果有待研究,且该方法可信度不高。
解决引清流量优化分配问题,关键在于如何平衡求解的精度与效率。精度与效率相互制约,在解决实际问题时常会顾此失彼。以物质守恒原理为基础,构建流量优化分配模型,目的是方便采用传统优化算法进行求解,但该方法因忽略各河段水动力对污染物的影响,因此求解结果的误差会偏大。而如果在优化模型中加入水动力模型,将会使模型的求解变得十分困难。笔者试图分析水动力对水质影响的原因,并把这种影响以参数的形式耦合到优化模型中,达到求解精度与效率的有效平衡。模型的优化结果就是每个河段应分配的流量。该优化结果可以用来指导内河中水工建筑物的流量调控。
1 流量分配优化模型
1.1 模型概化
在传统水质水动力耦合模型中,水动力模型为水质模型提供流量、流速等水动力要素基础,其中流速关系到物质的衰减量。若不考虑物质的衰减,则河段的污染物浓度仅是流量的函数,所以,可在不考虑物质衰减的情况,对各河段进行流量分配,然后,通过求解水动力模型,得出在对应流量下的各河段水流流速,从而计算各河段的污染物衰减作用。通过流量分配校正模型对各河段流量进行校正,得到各河道最终的流量分配数据,进而可以利用水工建筑物进行流量调控,得到满足水质要求的调控方式。此优化方法需要满足一些条件:①各河段水流单向流动;②各河段流量基本稳定;③在河道的入河排污口进行分段。
1.2 目标函数

调度方案的优劣可以表达为引水所耗费用的大小,其为各个引水河段流量的函数:式中:F为费用,元;qri为第ri河段的河道流量, m3/s;g为引水河道数。若河网总的分段数为n个,为了表达方便,把第n+1个河段作为虚拟河段,该河段连接所有的引水河段,其排入虚拟河段的污染物为0。
1.3 约束条件
a.忽略物质衰减的污染物守恒约束。

式中:qj为第j个河段污水入流之前的河道流量, m3/s;q忆j为第j个河段的污水流量,m3/s;qi为第i个河段污水入流之前的河道流量,m3/s;q忆i为第i个河段的入河污水流量,m3/s;eij为河道节点关系, [eij]n×n+1表示河道的上游连接矩阵,其中元素取值方式为:若j河段是i河段的上游河段,则eij=1,否则eij=0;Ei为其第i行行向量;籽j为第j条河道的污染物质量浓度,mg/L;Qh为河段流量与污水流量之和组成的行向量,Qh=[qi+]1×n+1;n为实际河段总数;籽i为第i个河段的污染物质量浓度,mg/L;籽忆i为第i个河段的污水浓度,mg/L。
b.节点流量守恒约束。

式中:Z=[zij]m×n+1,为节点的连接矩阵,其中元素取值方法为:若j河段为节点i的上游河段,则zij=1;若为其下游河段,则zij=-1,其他情况下,zij=0。Q为河段流量组成的行向量,Q=[qi]1×n+1;T= [tij]m×n+1,tij为节点入流河段的标识数,当j河道为i节点的出流河段时,tij=1,否则tij=0;W= [wj]n+1×1,wj为第j个河段的污水流量。
c.河段水质约束。

2 考虑物质衰减的河段引清流量修正
2.1 污染物衰减影响因素分析
对于一般条件下的河流,由推流导致的污染物迁移作用要比其弥散作用大得多,因此稳态条件下可以忽略弥散作用,得到概化河段始末污染物浓度的关系式[6]为:

式中:籽末为河段末的污染物质量浓度;籽初为河段初的污染物质量浓度。K为污染物衰减系数;ux为沿x方向河段流速;l为河段长度。
由公式(7)可知,河段流速为影响物质衰减的变量,而河段流速的值需要由水动力模型求解。可以先建立相应的水动力模型,通过水工建筑物的调控,使得河段流量为流量优化模型所求得的结果,进而计算河段流速。无法直接建立考虑污染物衰减的流量分配优化模型的原因是,河段的流量必须通过水动力模型求解,而把水动力水质耦合模型与优化方法结合起来非常困难。利用水动力模型提供的流速信息,对原流量分配方案进行修正是一种可行的方法。由于河段流量与河段流速有密切的关系,所以设定流量修正量是原流量的20%以内。水动力模型的控制方程为

式中:H为河道水位,m;Q为流量,m3/s;H忆为变化水位,m;A为过水断面面积,m2;B为过水断面宽度, m;q为单位长度河道的旁侧入流量,m3/(m·s); R为水力半径,m;c为谢才系数,c=R1/6/n,n为糙率系数;g为重力加速度,m/s2;x、t分别为位置和时间的坐标。
2.2 流量修正优化模型
流量修正优化模型如式(9)所示:
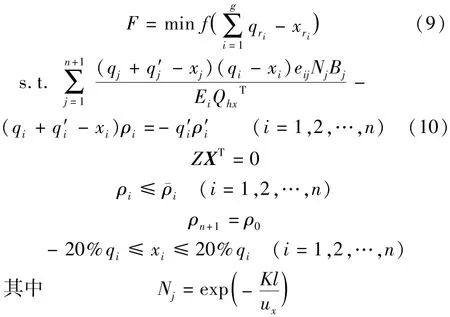
式中:xri为第ri河段流量的修正量;Bj为第j河段过水断面宽度,m;xi、xj分别为第i和第j河段流量的修正量;X为河道流量修正量的向量;Nj为j河段污染物衰减量的常数。
3 模型求解
3.1 罚函数法处理非线性约束
此模型针对单目标非线性优化问题,而非线性约束众多,属于大型非线性优化问题。考虑式(2),若仅把河段污染物质量浓度作为未知量,则形成了一个线性方程组,可用高斯消去法求解。故用罚函数法把非线性约束处理到目标函数中[7],可以形成如下优化问题,见式(11)~(12):

式中:M为惩罚因子。
经过处理后,优化模型中仅存在线性约束,且仅存在河段流量类的决策变量,利用数值方法进行计算时,流量被当成常数代入目标函数,这时存在于目标函数中的污染物质量浓度就可以通过求解线性方程组求出。但这样出流后目标函数不再可导,故需选择不依赖导数的求解方法进行求解。
3.2 带有线性约束的模式搜索法
带有线性约束的模式搜索法不需要导数信息,特别适合目标函数不可导且惩罚项较多的优化问题。文献[8]所提出的带有线性约束的模式搜索法能够较好求出平稳点且具有较强的全局性。方法中起作用的约束集如式(12)所示:
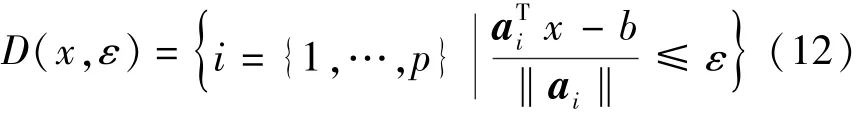
式中:D(x,着)为x处的着约束集,x∈B忆,B忆={x},∈Rp×n,为线性约束A忆x≥b的系数矩阵,ai为A忆中行向量。
从式(12)可以定义x处的着法锥N(x,着)与着切锥T(x,着):
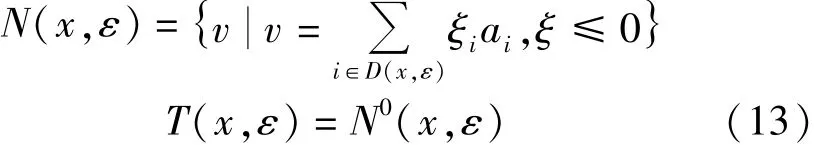
条件1:存在一个常数资min>0(通过式(14)计算),该常数与迭代步l无关,使得对每步都有着切锥不为空集,且兹l(l步的模式集合)能够生成该步的着切锥,且满足资(兹l)≥资min。
条件2:存在独立于迭代步长l的茁max≥茁min>0,对每个l都有着切锥不为空集,且对于所有的d∈兹l,茁min≤‖d‖≤茁max。
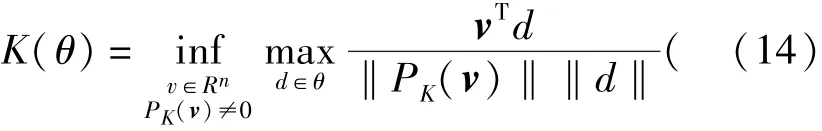
式中:K为由兹生成的凸锥体,PK(v)表示向量v在椎体K上的投影。d为模式,Rn为n维向量空间。在文献中[9]给出了一些模式的值,这些模式能够生成Rn。
带有线性约束的模式搜索法步骤如下:
第1步:初始化。令x0∈B作为初始点。令驻tol>0作为步长的缩放因子的容许值。令驻0>驻tol为初始缩放因子。令着max>茁max驻tol作为识别临近约束的最大距离。
第2步:选择模式。令着l=minx,茁max选择一组模式Dl=兹l∪Hl满足条件1与条件2,其中Hl为兹l中元素的线性组合。

第5步:下轮迭代。令l=l+1,返回第2步。
4 实例应用
为了改善福州市内河的水质,在规划截污80%的基础上,决定引调闽江水改善内河水质。引清调度路线、河流规划流向及河流分段如图1所示。

图1 河流分段及引清调度路线示意图
福州内河水质要求为氨氮质量浓度不超过2mg/L。不计水闸调度的成本,仅考虑泵站抽水所需电费,模型的目标函数如式(15)所示:

式中:q96、q33、q30、q1,分别为96、33、30、1号河段流量;4167.2、3440两个值为推导出来的系数。
根据单位时间内排入水系的污染物总量,可以计算出所需的最小稀释水环境容量,其计算公式如式(16)所示:

式中:qs为引水流量,m3/s;籽s为引水中污染物浓度,mg/L;q为污水入流之前的河道流量,m3/s;q忆为入河污水流量,m3/s;籽忆为河道的污染物质量浓度, mg/L;¯籽河道的污染物质量浓度上限,mg/L。
若不考虑经济因素与河网空间特征,由公式(16)可以得出理论最小引水流量为31.2m3/s。
根据模式搜索法的原理,不同的初始点会对模型的求解结果产生影响[9鄄10]。例如初始点分别为(1,0,1)与(2,3,1),在一个搜索模式[1,0,0]下,下一个计算点分别为(2,0,0)和(3,3,1)。分别设置3个在平均流量值附近的初始点,探讨算法对初始点的敏感性,模型的求解结果如表1和图2~4所示。3个初始点为:a1=[aij]96×1,aij=10;a2=[aij]96×1,aij= 15;a3=[aij]96×1,aij=20;图5为经过流量修正模型修正过后的河段流量分配结果。

图2 以a1为初始点的计算结果

图3 以a2为初始点的计算结果
从优化结果可知,初始点对模型的求解结果影响明显。以a1为初始点的优化中,部分河段水质没有满足要求,且计算的总引水量与试算法的结果持平,均为45m3/s。其中,以a3为初始点的优化结果中,总引水量远高于试算法的结果且水质仍有部分河段不满足水质要求。以a2为初始点的优化效果最好,各河段水质都能达到要求,且总引水量最小。优化算法计算最优的总引水量为37.81m3/s,相对于试算法,减少引水流量约7.2m3/s,且非常接近不考虑经济因素、河网空间特征及物质衰减情况下所需的引清流量31.2m3/s。

表1 福州内河不同河段污染物衰减量常数N值计算结果
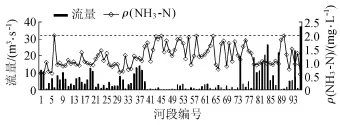
图5 修正后的流量分配及各河段的水质情况
5 结论与讨论
提出的优化模型充分考虑了引清调度系统的全局性,克服了试算法全局性较差且费时费力的缺点。此优化模型没有直接耦合水动力水质耦合模型与优化方法,而是在分析水动力模型对污染物衰减影响的基础上,先耦合水质模型与优化方法,然后利用水动力模型计算流速,对流量进行修正。耦合水质模型与优化方法,模型简单,易于求解,对流量修正引进了水动力模型对污染物的影响,因此该方法解决了水动力水质耦合模型与优化方法耦合优化模型难以求解的问题。在福州内河的应用表明,该优化模型能够计算出每个河段具体的引清流量及预期水质,统筹考虑整个河网的引清流量,大大减少了引清调度的成本。
但是,模式搜索法求解此优化模型的稳定性不佳,受初始点影响明显,因此寻求一种更有效的方法来求解此模型,是以后需要研究的问题。
[1]江涛,朱淑兰,张强,等.潮汐河网闸泵联合调度的水环境效应数值模拟[J].水利学报,2011,42(4):388-394. (JIANG Tao,ZHU Sulan,ZHANG Qiang,et al.Numerical simulation on effects of gate-pump joint operation on water environment in tidal river network[J].Journal of Hydraulic Engineering,2011,42(4):388-394.(in Chinese))
[2]徐贵泉,唐迎洲.崇明岛引清调水方式优化研究[J].中国农村水利水电,2011(2):4-7.(XU Guiquan,TANG Yingzhou.Research on the optimization of clean water diversion on Chongming Island[J].China Rural Water and Hydropower,2011(2):4-7.(in Chinese))
[3]朱淑兰.潮汐河网闸泵优化调度的水环境效应数值模拟[D].广州:中山大学,2010.
[4]CHO J H,SUNG K S,HA S R.A river water quality management model for optimizing regional wastewater treatment using a genetic algorithm[J].Journal of Environmental Management,2004,73(3):229-242.
[5]林高松,李适宇,陈璇.混合智能算法在引水冲污方案优选中的应用[J].水资源保护,2009,25(4):31-36. (LIN Gaosong,LI Shiyu,CHEN Xuan.Application of a hybrid intelligent algorithm in scheme optimization of water diversion to flush out pollutants[J].Water Resources Protection,2009(4):31-36.(in Chinese))
[6]汪家权,钱家忠.水环境系统模拟[M].合肥:合肥工业大学出版社,2005.
[7]姚恩瑜,何勇,陈仕平.数学规划与组合优化[M].杭州:浙江大学出版社,2001.
[8]KOLDA T G,LEWIS R M,TORCZON V.Stationarity results for generating set search for linearly constrained optimization[J].SIAM Journal on Optimization,2006,17:943-968.
[9]KOLDA TG,LEWISR M,TORCZON V.Optimization by direct search:new perspectives on some classical and modern methods[J].SIAM Review,2003,45:385-482.
[10]KOLDA TG,LEWISR M,TORCZON V.A generating set direct search augmented Lagrangian algorithm for optimization with a combination of general and linear constraints[R].Williamsburg:College of William& Mary,2006.
Flow allocation optim ization model of clean water diversion in com plex river networks
XUE Lianqing1,2,WANG Siqi2,XING Baolong2,DUAN Xiaolan3
(1.College ofWater Conservancy and Architectural Engineering,Shihezi University,Shihezi832009,China; 2.College ofHydrology and Water Resources,Hohai University,Nanjing 210098,China; 3.Fuzhou Planning Design and Research Institute,Fuzhou 350003,China)
A flow allocation optimizationmodel of clean water diversion in a complex river network was established based on the principle of conservation of matter,for the optimization of clean water diversion.In terms of the implicit function relationship between river water quality and flow,the penalty function method was used to deal with the nonlinear constraints in themodel.The water quality of the river was expressed by the objective function, so that decision variables and constraints were reduced.The model was solved by pattern search with different initial points,and the results show that the initial points can have a significant impact on the results.The impact of hydrodynamics was included in the correction model of clean water diversion in the form of parameters based on analysis of impact factors of pollutant attenuation,and the correction model of the clean water diversion was established.The correction model was applied to the calculation of diverted flow in the internal river of Fuzhou. The results show that the corrected flow,compared with that obtained by the testmethod,decreased by 7.2 m3/s, which means that the flow was greatly reduced and optimally allocated.
clean water diversion;flow allocation model;penalty function method;pattern search method
TV213.4
A
1004 6933(2014)05 0068 05
2013 11 29编辑:彭桃英)
10.3969/j.issn.1004 6933.2014.05.012
国家自然科学基金(41371052);新疆联合基金(U1203282);江苏“青蓝工程”及兵团创新团队人才计划
薛联青(1973-),女,教授,博士,主要从事环境水文及水环境保护研究。E-mail:lqxue@hhu.edu.cn
