文化基因粒子群算法在换热网络连续变量全局优化中的应用
2014-06-07何巧乐崔国民许海珠
何巧乐,崔国民,许海珠
(上海理工大学 能源与动力工程学院,上海 200093)
文化基因粒子群算法在换热网络连续变量全局优化中的应用
何巧乐,崔国民,许海珠
(上海理工大学 能源与动力工程学院,上海 200093)
在换热网络的综合优化中,连续变量的优化通常采用确定性方法。相比于整型变量优化,连续变量优化相对容易处理,但存在容易陷入局部最优和无法收敛到全局最优的问题。针对这一问题,提出一种在标准粒子群算法中结合局部搜索策略的文化基因粒子群算法;结合换热网络最小年综合费用小和计算时间短的优点,提出Ring+Random粒子种群拓扑结构;结合算法控制参数的设置与粒子种群拓扑结构的改进,使文化基因粒子群算法具有更好的全局收敛性能。采用6个10股流体算例验证文化基因粒子群算法在给定换热网络结构下的连续变量全局收敛性能,与文献值相比,换热网络最小年综合费用最大减少了26 025 $/a。
换热网络综合;粒子群算法;文化基因;连续变量全局优化;局部搜索
换热网络综合优化从20世纪80年代开始成为热点问题,期间发展出了大量有效的设计和处理换热网络的方法[1-2]。尽管换热网络综合是过程系统中广泛研究的问题之一,但到目前为止,即使小规模换热网络也无法证实寻找到全局最优解。因此,换热网络综合的优化复杂性使得特定优化算法有很大的发展空间[1]。
换热网络综合优化中通常采用确定性方法来处理连续变量。Athier等[3]采用局部优化程序库中NLP算法、Lewin等[4]采用Simplex算法、Errico等[5]采用Lindo-Lingo和CPLEX程序、Khorasany等[6-7]采用序列二次规划算法(SQP)来优化连续变量。但在确定性方法中初始点的选择起到至关重要的作用,如果提供一个较差的初始点,优化可能无法收敛或收敛到一个较差的局部极值点。同时,基于二阶导数的局部搜索程序的应用,大大增加了换热网络综合的优化难度。
由于启发式方法可以处理传统优化方法难以解决的问题,所以在近年来的发展中比较倾向于在同步优化中采用启发式算法。不同于确定性方法中采用基于梯度的优化方法来处理连续变量,启发式方法采用追踪种群中的有利潜在解。因此,初始点的选择对于启发式方法不敏感,从而保证不容易陷入局部最优解。
粒子群算法作为启发式方法中的一种在换热网络中应用的相对较少。2009年,严丽娣等[8]采用标准粒子群算法对无分流换热网络进行同步优化。夏涛等[9]提出遗传算法优化换热网络结构,标准粒子群算法优化换热量的混合算法。Silva等[10]应用标准粒子群算法进行同步优化分流换热网络。霍兆义等[11]提出混合算法优化换热网络结构,内层在固定换热网络结构下利用标准粒子群算法优化连续变量。
但上述文献中没有提及标准粒子群算法在换热网络综合优化中的具体实现步骤,无可重复性,也缺少连续变量优化全局收敛性的验证。而且标准粒子群算法本身也存在一些缺陷,其虽能有效地探测到全局最优解区域,但进入该区域后无法以高精度进行局部收敛。同时,在标准粒子群算法中粒子获得的最优信息不是此区域内的严格局部极值将导致种群的过度迭代更新。上述缺陷使基于下层连续变量优化费用的混合算法和双层优化算法的性能大幅降低。
本工作首先用4股流体算例分步骤阐述标准粒子群算法在换热网络综合优化中的实现;提出用标准粒子群算法结合局部搜索策略的文化基因粒子群算法(MPSO)来处理混合算法中下层连续变量优化;用一个8股流体算例中的原始结构和6个10股流体算例中的原始结构进行连续变量优化来验证MPSO算法在换热网络连续性变量优化中的全局搜索能力。
1 标准粒子群算法在换热网络中的实现
标准粒子群算法是由Kennedy等[12]在1995年提出的基于群智能的启发式优化方法。首先采用一个小规模算例来分步骤阐述标准粒子群算法在换热网络综合中的具体实现。该算例为2股热流体和2股冷流体的4股流体综合问题,流体数据取自文献[13](见表1)。以换热网络最小年综合费用为优化目标函数。
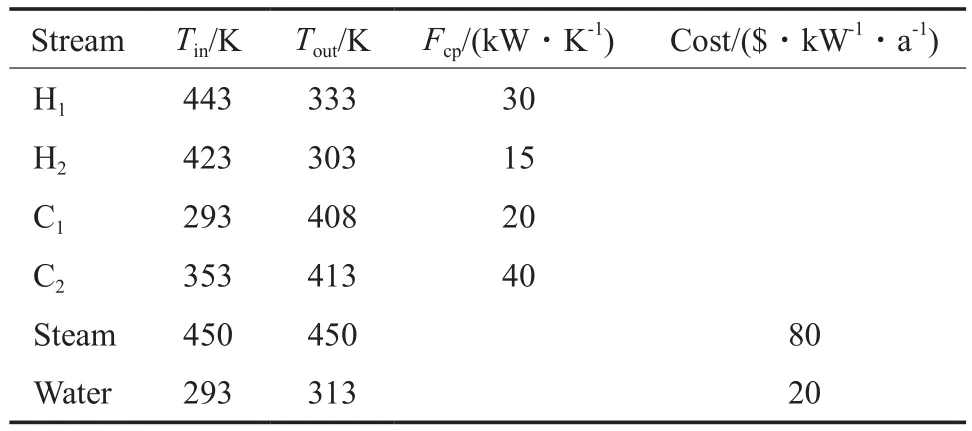
表1 4股流体算例的流体数据[13]Table 1 Stream data for case of 4-stream problem[13]
第一步参数输入。粒子种群大小N=100;学习因子c1=0.5,c2=0.5;惯性因子ω=0.5;计算最大迭代步数Iteration为1 000;粒子更新累积次数NPRN=20步,进行终止判定;换热网络级数k = max(NH,NC),向量维数(换热器的个数)d=NHNCk。
第二步粒子初始化。N组d维优化变量(换热器面积)初始化为xi=(xi1,xi2,…,xid)= rand( )×5,i=1,2,…,N,rand( )是取值介于(0,1)之间的伪随机数,初始面积取值(0,5)。N组d维粒子速度初始化为:vi=(zi1,vi2,…,vid)= rand( )。
第三步换热网络约束处理。传统换热网络模拟计算先构建一个包含所有潜在换热器d = NHNCk = 8的换热网络。分别已知冷、热流体的入口温度Tini(i=1,2,…,NH),Tinj(j=1,2,…,NC)和冷、热流体的末端目标温度Touti(i=1,2,…,NH),Toutj(j=1,2,…,NC)。4股流体换热网络的结构见图1。
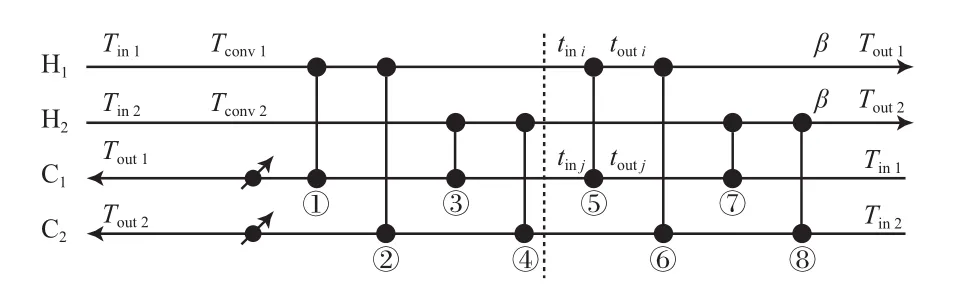
图1 4股流体换热网络的结构Fig.1 Schematic representation of a 4-stream heat exchanger networks.Tini:inlet temperature;Touti:outlet temperature;Tconvi:convergence temperatures at hot stream inlet in the iteration;β: convergence temperatures at hot stream outlet in the iteration.
换热网络模拟计算的迭代过程从第8号换热器开始(不同于夏涛等[9]以换热量为优化变量,从第1号换热器开始计算)。当计算完最后一个换热器(第1号)后热流体入口温度小于流股初始值时,在热流体末端加冷却器,将温度向上平移直到热端:

当式(1)条件满足时,如果热流体末端出口温度β小于流体目标温度时,则认为不满足约束。在处理上述约束时不采用传统的惩罚函数,将以上约束情况转化为无约束问题继续求解,取而代之在βi<Touti时(即不满足约束时)在末端加一个“加热器”,使其达到目标温度,计算换热网络所需真实的换热网络最小年综合费用。
根据夹点原理,在夹点以下不允许出现“加热器”。但值得注意的是在优化过程中热流体不满足温度约束时采用“加热器”处理,最后的优化结果中不会存在此类“加热器”(从算例中得到验证)。事实上,此类“加热器”的存在导致能量的不合理利用从而引起整体换热网络最小年综合费用大增,相当于对不满足约束情况进行了一个大的惩罚。所以对没有精确一维线性搜索的标准粒子群算法采用“加热器”处理不满足约束情况是合适的。
对单个换热器的计算,同时要求换热的冷热流股之间满足如下约束:

式中,i为热流体,j为冷流体,具体如图1中第5号换热器所示。如果不满足以上约束,则认为热流体不能将冷流体加热到Toutj;冷流体不能将热流体冷却到Touti。此两股流体之间暂不存在换热器,换热面积为0。
第四步粒子位移速度更新。粒子通过自身与群体最优信息更新换热面积及飞行速度。4股流体算例中每一个粒子具体状态更新过程见表2与表3。

式中,学习因子c1和c2是非负常数;γ1和γ2是取值介于(0,1)之间的伪随机数。

表2 粒子第1次迭代的结果Table 2 The best position of each particle and the overall best position recorded in 1stiteration
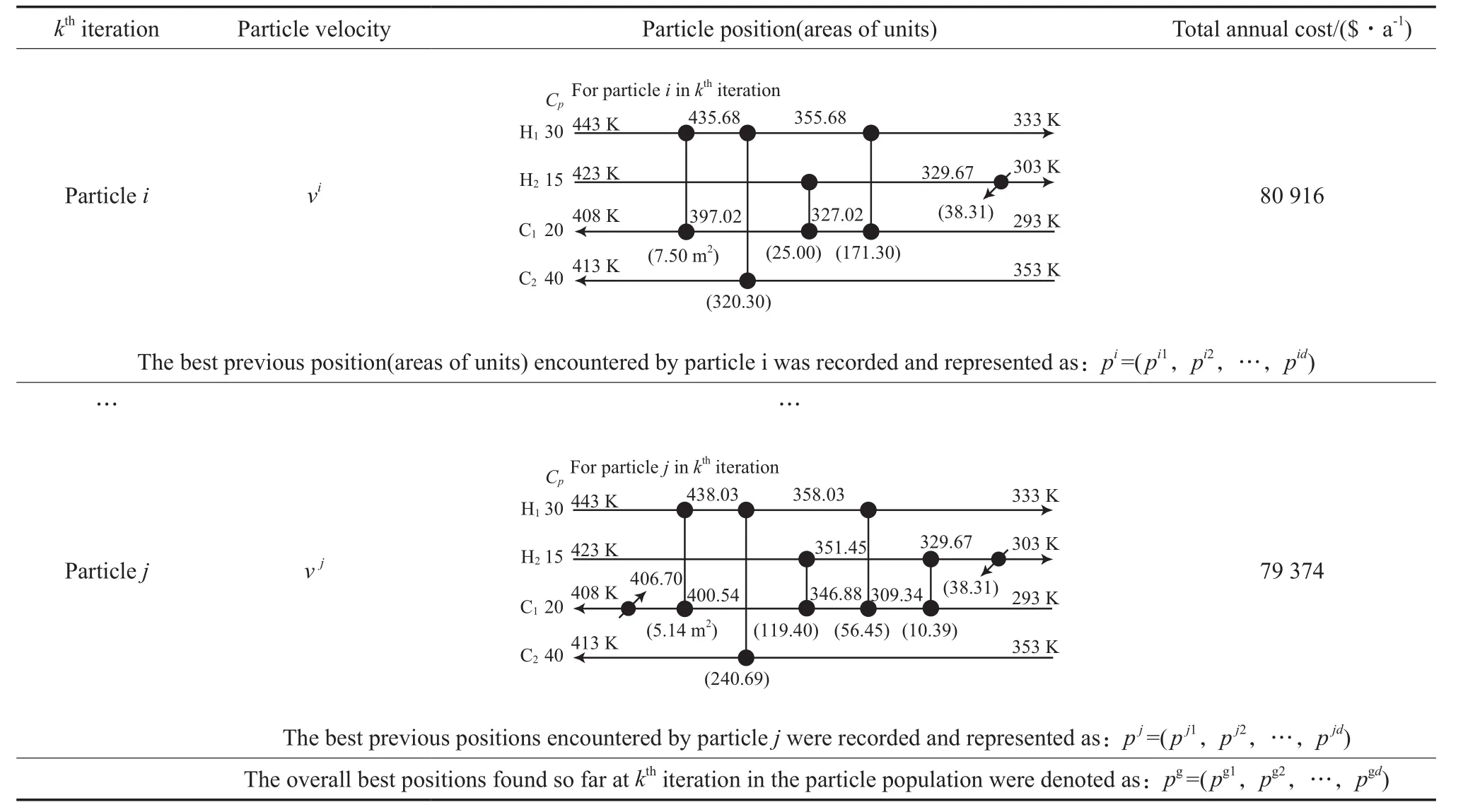
表3 粒子第k次迭代的结果Table 3 The best position of each particle and the overall best positions recorded in kthiteration
第五步终止条件。重复步骤四,直到满足迭代终止条件。在Iteration为1 000次中, NPRN=20次后换热网络最小年综合费用不再变化则跳出;否则运行到最大迭代次数跳出。记录下最优的换热网络面积及换热网络最小年综合费用。
至此给出了可重复性实验的优化换热网络的标准粒子群算法。图2是标准粒子群算法优化4股流体算例得到的最优换热网络结构。

图2 标准粒子群算法优化4股流体算例获得的最优换热网络结构Fig.2 The optimal heat exchanger network confguration of the 4-stream problem obtained by standard particle swarm optimization.
2 标准粒子群算法控制参数的设置
标准粒子群算法和其他算法一个显著不同就是所需调整参数较少,其参数主要包括:惯性因子(ω);飞行速度限制[-vmax,vmax];学习因子(c1,c2);种群大小;初始面积。
参数的合理设置有助于准确并有效地搜索到最优解。在文献推荐值的基础上,通过增加参数或改变原有设定参数,以达到提高算法搜索效率的目的。学习因子采用c1=c2=0.5的设置,通常能在搜索时间缩短的基础上找到最优解。在换热网络优化中,标准粒子群算法对种群规模不敏感,但不宜过小,在计算中始终保持种群规模为100。标准粒子群算法为全局最优化方法,与基于梯度的局部优化算法跟初始面积密切相关不同,标准粒子群算法作为连续变量的全局最优化与初始面积无关。
2.1 惯性因子
ω的作用主要体现在速度更新中保持原有飞行速度的权重:ω较大时算法有较强的全局搜索能力,同时也需要消耗更多的迭代时间;ω较小时算法的局部搜索能力较强。在实际换热网络优化中,总希望在优化初期全局开发能力较强,在算法收敛于某一个区域后,具有较强较高精度的局部搜索能力。所以采用以下2种ω来观察换热网络优化的性能:1)将ω随迭代由0.8线性递减到0.3:ω = 0.8 -iter/itermax(0.8 - 0.3);2)ω = 0.5 + rand/2。
用上述2种ω及标准粒子群算法中的固定取值进行计算,计算时间和换热网络最小年综合费用见表4。从表4中得出,方案1)中的“线性”递减策略虽仍不能反映实际优化的非线性搜索过程,但相比于固定惯性权重方案2),动态变化的ω的换热网络最小年综合费用(79 229 $/a)更小,所以采用ω = 0.8 - iter/itermax(0.8 - 0.3),但增加一些计算时间。

表4 不同ω下的计算时间及换热网络最小年综合费用Table 4 Calculation time and total annual cost at different inertia factors(ω)
2.2 最大飞行速度限制
传统的标准粒子群算法通常将粒子飞行速度限制在[-vmax,vmax]中,超过边界值时取边界值。最大飞行速度(vmax)与计算时间和换热网络最小年综合费用的关系见图3。由图3可见,vmax=20时,飞行区域限定过小,会迅速陷入局部最优而且不易跳出,体现为计算时间短、换热网络最小年综合费用值大;vmax=250~1 000时计算时间和换热网络最小年综合费用不变化;不采取飞行速度限制,在换热网络模拟中偶尔会出现在粒子更新多代后某个换热器面积急剧增加(面积爆炸),无法进行换热网络模拟计算。
随vmax的增大陷入局部最优的可能性减小。所以为增加全局搜索能力,vmax采用在换热网络模拟中不会出现“面积爆炸”的一个较大值,如vmax=1 000。

图3 vmax与计算时间及换热网络最小年综合费用的关系Fig.3 Variation tendency of calculation time and total annual cost with velocity limitation(vmax).
3 MPSO算法
为了使标准粒子群算法有更好的连续变量全局收敛性能,提出结合局部搜索策略的MPSO算法,同时结合粒子种群拓扑结构的改进。
MPSO算法并行追踪种群中的有利潜在解,具有初始点的选择对于启发式方法不敏感的特点,从而保证不容易陷入局部最优解。同时克服了标准粒子群算法的一些缺陷:在探测到全局性区域后能以高精度进行局部收敛,相应地减少粒子的迭代更新,使采用MPSO作为下层连续变量优化的混合算法和双层算法性能大幅提高。
3.1 粒子种群拓扑结构
标准粒子群算法是基于群智能的优化技术,搜索过程可理解为在多维空间中,粒子记忆个体最优解并且共享种群内最优信息。种群拓扑结构就是种群中粒子的信息传递模式,通过改变粒子传递信息的方式可以提高MPSO算法的全局搜索能力。
4种不同的粒子种群拓扑结构见图4。图4中Global topology,Random topology,Ring topology粒子种群拓扑结构来自文献[12]。分别将上述3种粒子种群拓扑结构进行计算,得到计算时间和换热网络最小年综合费用(见表5)。

图4 4种不同的粒子种群拓扑结构Fig.4 Topology representations of the four kinds of different particles. i:the arbitrarily chosen particles in the population.
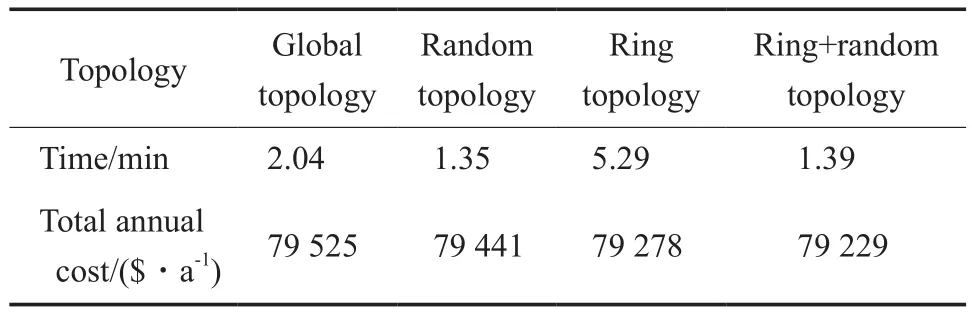
表5 4种粒子种群拓扑结构下的计算时间及换热网络最小年综合费用Table 5 Calculation times and least total annual costs with four different topologies.
结合图4和表5可知,Global topology粒子种群拓扑结构的最优信息交换快,粒子能迅速感知群体最优而向其运动,但陷入79 525 $/a的局部最优,原因在于粒子间过快分享了“群体最优”信息;Random topology粒子种群拓扑结构从种群中随机选取n个粒子而非整个种群进行信息交换,与Global topology相比缩短了计算时间,且由于粒子间群体最优信息共享速率的减慢增强粒子“逆搜索”,获得比Global topology好的换热网络最小年综合费用79 441 $/a;Ring topology粒子种群拓扑结构由于只跟(i+1)和(i-1)两个相邻粒子共享信息,局部搜索程度大幅增加,所以计算时间较长,但可获得最小的换热网络最小年综合费用79 278 $/a。
因此为了搜索到更好极值的同时能兼顾计算效率,需要有效限定群体最优信息在整个种群的共享速度,让粒子多利用自身经验在解空间进行逆搜索。所以结合Ring topology优化换热网络最小年综合费用小的优点和Random topology的计算时间短的优点,提出Ring+Random粒子种群拓扑结构(图4)。从表5可看出,Ring+Random粒子种群拓扑结构在换热网络最小年综合费用和计算时间上是有利的。
3.2 局部搜索
粒子根据记忆自身最优与共享群体经验探测全局最优区域。但存在粒子i的“自身经验”项最优信息量小而导致粒子飞行方向不准确而频繁更新速度。因此,提出两种局部搜索策略来搜索出粒子当前解邻域内的局部最优并且记录,以提高基于“自身经验pi”和“群体经验pgk”的迭代更新的准确性,确保算法更有利探测到全局最优区域并以高精度收敛。
3.2.1 局部搜索策略Ⅰ
对于每一个粒子i,利用粒子的当前有利飞行方向v,向前后飞行不同的步长λ来构造新的不同的可行解。即在粒子i邻域内构造nstep个点进行换热网络模拟计算,记录邻域内最优信息用于更新。
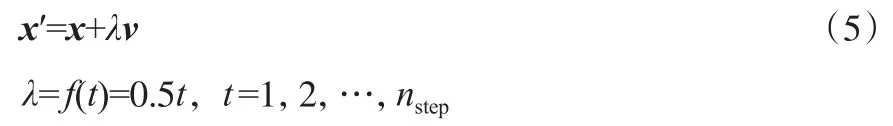
通常,nstep的取值越大锁定全局最优解的可能性更大,但同时会大幅延长计算时间。为了保证计算高效,nstep通常设定在区间[15,20]。
3.2.2 局部搜索策略Ⅱ
策略Ⅰ中每个面积的增加步长是一致的,以下提出一种顺序增加面积的局部搜索方法:

借鉴“坐标轮换优化法”的特性,引入坐标方向sk,表示第k个为1的单位坐标向量,例如k=1时,s1=(1,0,…,0),只增加第一个换热器面积,循环nstep次记录最优面积;依次计算换热器直到k=d时,sd=(0,0,…,1),仍循环nstep次记录最优面积。即依次按多维空间的坐标轴方向进行局部搜索,记录邻域内最优信息用于更新。步长λ的设置如同策略Ⅰ。
局部搜索策略Ⅰ和Ⅱ各有特点:局部搜索策略Ⅰ计算速度更快,其简单易用性使其能应用于所有算例,特别是工业级别的换热网络综合优化;局部搜索策略Ⅱ计算精度高但费时,更适合应用于有换热器固定投资费用的综合优化问题。
标准粒子群算法结合局部搜索进行换热网络优化时会由于局部搜索相应增加计算量,但能找到更好的极值点,以下用算例进行验证。
3.3 算例验证
利用基准测试函数Trefethen和Drop Wave验证MPSO算法在连续变量优化中的全局搜索能力,均搜索到了全局最优点。
对文献[13]中8股流体算例[14]的换热网络结构采用MPSO算法进行固定结构(没有整型变量优化)下的连续变量优化,验证MPSO算法在固定结构下的全局搜索能力。优化结果对比文献[13]多出12 $/a,原因在于MPSO算法的精度没有确定性方法高,且对于小规模网络优化,确定性方法往往通过多起点搜索到全局性的解。所以在小型换热网络的优化中,MPSO算法得到的换热网络最小年综合费用会由于精度的影响略大一些。
用10股流体算例进行验证,以突出MPSO算法在换热网络固定结构下的连续变量优化全局性搜索能力。10股流体算例的流体数据取自文献[15],见表6。
例如针对引流工作而言,应当能够妥善保护现有的现场引流设施,避免此类设施呈现破损现象。对于整个施工区有必要配备相应的基础设施,通过运用详细规划的方式来保证上述设施能够达到应有的可靠性与坚固性。
将文献[6,15-19]中6个10股流体算例的优化结构作为给定固定结构,分别采用MPSO算法进行固定结构下连续变量的优化,换热网络年综合最小费用均好于原文献。
对文献[16]采用MPSO算法优化得到的最优换热网络结构见图5。与文献[16]中的换热网络结构相比,MPSO算法重新合理地分配换热量在换热网络结构中的分布,取消了一个换热器。与用局部优化方法[16]优化得到的换热网络最小年综合费用为5 631 380 $/a相比,采用MPSO算法优化后换热网络最小年综合费用减少了1 427 $/a。

表6 10股流体算例流体数据参数[15]Table 6 Stream data and cost parameters for 10-stream problem[15]
对文献[6,15]采用MPSO算法优化得到的最优换热网络结构见图6。与文献[6,15]中的换热网络结构相比,MPSO算法更合理地分配换热量,从而使换热网络最小年综合费用大幅降低。与文献[15]中用遗传算法优化得到换热网络最小年综合费用为5 666 755 $/a,与文献[6]中用SQP优化连续变量得到换热网络最小年综合费用为5 662 366 $/a相比,采用MPSO算法优化后的换热网络最小年综合费用为5 640 730 $/a,分别减少了26 025,21 636 $/a。
此外,采用MPSO算法优化,文献[17]中的换热网络最小年综合费用降至5 642 385 $/a,减少了约4 000 $/a;文献[18]中的换热网络最小年综合费用降至5 660 569 $/a,减少了504 $/a;文献[19]中的换热网络最小年综合费用降至5 666 752 $,减少了4 $/a。

图5 对文献[16]采用MPSO算法优化得到的最优换热网络结构Fig.5 Optimal heat exchanger networks obtained by memetic particle swarm optimization(MPSO) compared with Ref.[16].
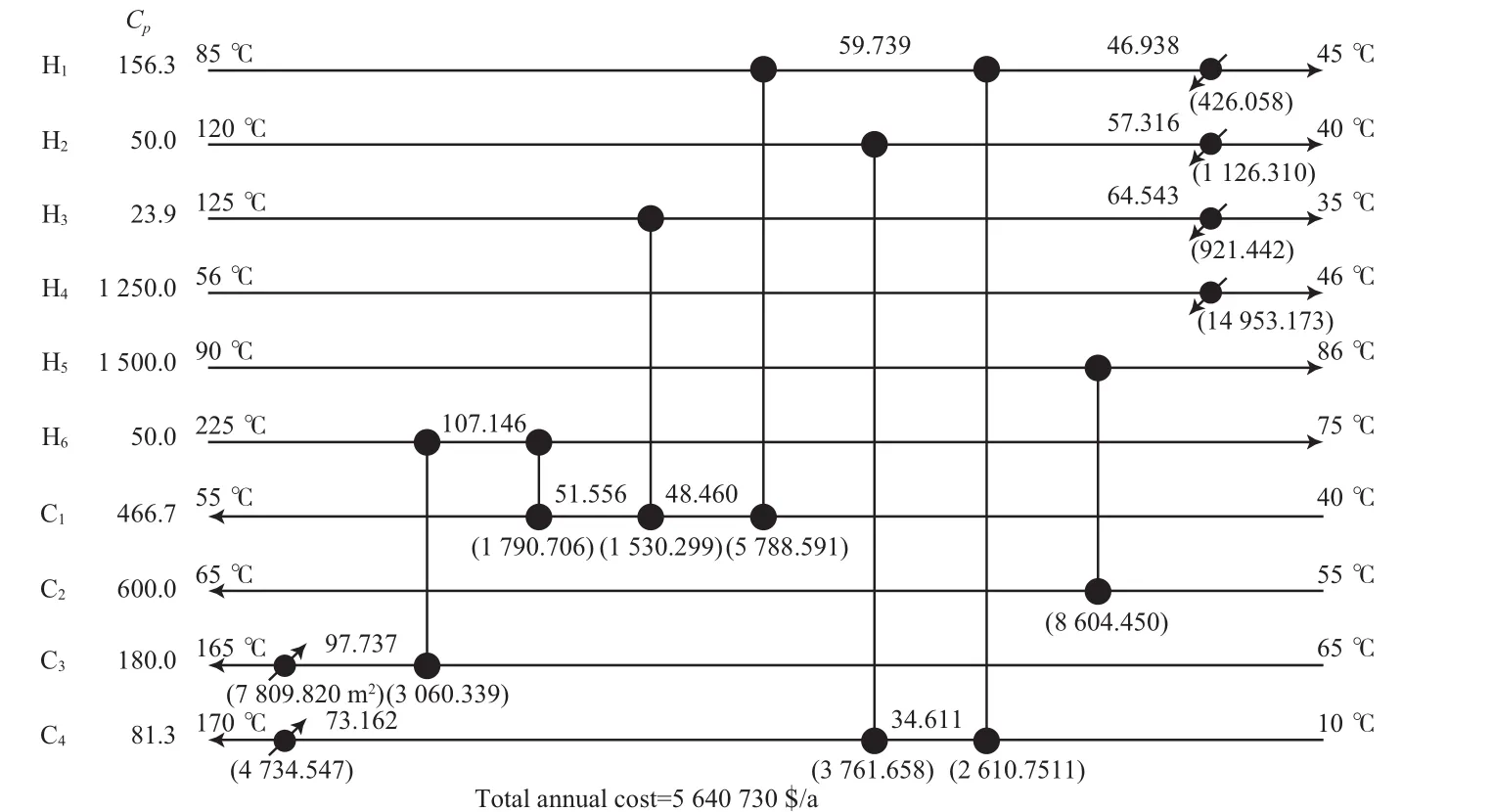
图6 对文献[6,15]采用MPSO算法优化得到的最优换热网络结构Fig.6 Optimal heat exchanger networks obtained by MPSO compared with Ref.[6] and[15].
以上6个10股流体算例的结构经过MPSO算法优化后换热网络最小年综合费用均有下降。因为标准粒子群算法不同于确定性方法敏感于初始值的选取而且容易陷入局部最优,同时在加入局部搜索后的MPSO算法能更有效地调节换热量的分配,从而产生换热网络最小年综合费用更小的结构。
4 结论
1)在标准粒子群算法在无分流换热网络中实现应用的基础上,提出了MPSO算法。结合标准粒子群算法控制参数的设置和粒子种群拓扑结构的改进,使MPSO算法在双层优化中的下层连续变量优化中具有更好的全局搜索能力。
2)结合Ring topology优化换热网络最小年综合费用小的优点和Random topology的计算时间短的优点,提出Ring+Random粒子种群拓扑结构。提出两种不同步长变化的局部搜索策略,在探测到全局性区域后能以高精度进行局部收敛,并相应地减少粒子的迭代更新。策略Ⅰ计算快速因而适用于大规模算例;策略Ⅱ精度高,更适合于考虑固定投资费用的算例。基于以上改进提出的MPSO算法性能大幅提高,适合用于优化较复杂的连续变量换热网络。
符 号 说 明
A 换热器换热面积,m2
Cp热容,kJ/K
c1,c2学习因子
d 向量维度(换热器总个数)
Fcp流体热容流量, kW/K
iter 粒子当前迭代数
k 换热网络级数
N 粒子种群规模大小或流股个数
NPRN 粒子更新累积次数
nstep局部搜索次数
p 粒子位置
p 粒子自身最优位置向量
pg种群最优位置向量
rand 取值介于(0,1)的伪随机数
s 单位坐标向量
T 流体温度,K
U
流体传热系数,kW/m2
v 粒子速度
v 粒子速度向量
x 换热器面积
x 粒子位置向量
β 热流体末端出口温度,K
γ 取值介于(0,1)的伪随机数
λ 步长
ω 惯性因子
下角标
C 冷流体
conv 收敛值
H 热流体
i 热流体
in 流体入口
j 冷流体
k 粒子当前迭代次数
max 最大值
out 流体出口
上角标
i,j 粒子
d 换热器
g 全局最优
[1] Furman K C,Sahinidis N V. A Critical Review and Annotated Bibliography for Heat Exchanger Network Synthesis in the 20th Century[J]. Ind Eng Che Res,2002,41(10):2335 - 2370.
[2] Morar M,Agachi P S. Review:Important Contributions in Development and Improvement of the Heat Integration Techniques[J]. Comput Chem Eng,2010,34(8):1171 - 1179.
[3] Athier G,Floquet P,Plbouleau L,et al. Process Optimization by Simulated Annealing and NLP Procedures:Application to Heat Exchanger Network Synthesis[J]. Comput Chem Eng,1997,21(S):S475 - S480.
[4] Lewin D R,Wang H,Shalev O. A Generalized Method for HEN Synthesis Using Stochastic Optimization:Ⅰ. General Framework and MER Optimal Synthesis[J]. Comput Chem Eng,1998,22(10):1503 - 1513.
[5] Errico M,Maccioni S,Tola G,et al. A Deterministic Algorithm for the Synthesis of Maximum Energy Recovery Heat Exchanger Network[J]. Comput Chem Eng,2007,31(7):773 - 781.
[6] Khorasany R M,Fesanghary M. A Novel Approach for Synthesis of Cost-Optimal Heat Exchanger Networks[J]. Comput Chem Eng,2009,33(8):1363 - 1370.
[7] Toffolo A. The Synthesis of Cost Optimal Heat Exchanger Net-works with Unconstrained Topology[J]. Appl Therm Eng,2009,29(17/18):3518 - 3528.
[8] 严丽娣,霍兆义,尹洪超. 粒子群算法最优同步综合换热网络[J]. 化工进展,2009,28(S1):439 - 442.
[9] 夏涛,贾涛,程杰. 群智优化算法同步综合换热网络[J]. 北京化工大学学报:自然科学版,2009(1):97 - 101.
[10] Silva A P,Ravagnani M A S S,Biscaia Jr E C,et al. Optimal Heat Exchanger Network Synthesis Using Particle Swarm Optimization[J]. Optim Eng,2010,11(3):459 - 470.
[11] 霍兆义,赵亮,尹洪超,等. 基于群体智能算法的换热网络同步最优综合[J]. 化工学报,2012(4):1116 - 1123.
[12] Kennedy J,Eberhart R. Particle Swarm Optimization[J]. Neural Network,1995,4:1942 - 1948.
[13] He Qiaole,Cui Guomin. A Principle of Stream Arrangement Based on Uniformity Factor for Heat Exchanger Networks Synthesis[J]. Appl Therm Eng,2013,61(2):93 - 100.
[14] Grossmann I E,Sargent R W H. Optimum Design of Heat Exchanger Networks[J]. Comput Chem Eng,1978,2(1):1 - 7.
[15] Ravagnani M A S S,Silva A P,Arroyo P A,et al. Heat Exchanger Network Synthesis and Optimisation Using Genetic Algorithm[J]. Appl Therm Eng,2005,25(7):1003 - 1017.
[16] 胡向柏. 换热网络全局优化[D]. 上海:上海理工大学,2013.
[17] 赵亮,霍兆义,李栋斌,等. 无分流换热网络同步优化综合[J]. 热科学与技术,2013(1):68 - 73.
[18] 涂惟民. 换热网络全局最优化研究[D]. 上海:上海理工大学,2011.
[19] Yerramsetty K M,Murty C V S. Synthesis of Cost-Optimal Heat Exchanger Networks Using Differential Evolution[J]. Comput Chem Eng,2008,32(8):1861 - 1876.
(编辑 李治泉)
·技术动态·
中国石化抚顺石化院等开发FFI蜡油加氢与催化裂化技术
中国石化抚顺石油化工研究院与洛阳分公司共同研发的FFI 蜡油加氢处理与催化裂化深度组合系列技术,通过了中国石化科技部组织的技术鉴定。中型试验和经济评价结果表明,该技术能够有效增产高价值的催化裂化汽油和液化气产品。应用蜡油加氢处理与催化裂化FFI 深度组合技术,蜡油加氢处理装置可取消产品分馏系统,全馏分加氢生成油直接热供料去催化裂化装置加工,再经蜡油加氢装置处理后返回到催化裂化装置加工。采用FFI 系列技术对蜡油加氢处理与催化裂化装置进行了技术改造。工业装置运行结果表明,与改造前相比,加氢装置能耗、柴油收率、焦炭收率明显降低,汽油硫含量有所降低,催化轻质油收率、轻液体收率、汽油收率、催化汽油研究法辛烷值得到提升。该系列技术已申请4项中国发明专利。
中国石化完成国Ⅲ柴油升级
截至2013年5月底,中国石化生产的柴油全部达国Ⅲ标准要求,提前一个月完成升级任务。截至目前,中国石化已在10家企业建成投产10套催化汽油吸附脱硫装置(Szorb),另有7套Szorb装置年底前将陆续建成投产,再加上对另外相关企业的汽油加氢等装置进行技术改造等,2014年中国石化可全面供应国Ⅳ车用汽油,实现了中国石化将于2015年起供应符合国Ⅳ标准的车用柴油的承诺。
中国石油石油化工研究院高效聚丙烯催化剂试产成功
中国石油石油化工研究院自主开发的高效聚丙烯催化剂(PSP-01)进行工业应用,试产聚丙烯新产品高速双向拉伸聚丙烯薄膜专用料T36FD,获得成功。石油化工研究院与炼化企业密切合作,通过进一步优化催化剂和聚合工艺,精确控制产品熔融指数,改善加工性能,推出新牌号T36FD。新产品开发工业试验连续平稳运行59 h,累计生产T36FD新产品1 555 t,产品质量稳定。
大庆石化乙烯裂解装置通过标定
大庆石化公司新建600 kt/a乙烯装置经过72 h满负荷运行,系统温度、压力和大设备机组运行参数均达到设计指标,乙烯日均产量达到1 869 t,乙烯收率达到30.57%,装置运行一次通过标定。大庆石化公司600 kt/a乙烯装置2012年9月投产。该公司通过对前冷系统、碳二加氢反应器和碱洗塔的优化改造,使装置能效进一步提升。为准确掌握装置运行数据,该厂对原料、产品、辅助材料、公用工程和环保等十多个项目的上万组数据进行采集和分析评价,使装置运行的各项指标达到最佳值。标定期间,该公司化工一厂和质量检验中心严格制订标定方案,对原料、侧线产品和裂解气组成等60多个关键数据化验分析,采集数据上万个,保证装置标定全面受控。
青岛能源所合成两生物基化学品
中国科学院青岛生物能源与过程研究所在生物法合成甲基乙偶姻(3-甲基-3-羟基-2-丁酮)和2-甲基-2,3-丁二醇的研究中取得进展。由于在自然界中尚未发现这两种化合物完整的生物合成途径, 因此,需要在微生物体内设计和构建非天然的合成途径。为了使其成为具有经济竞争力的理想生物合成途径,需要获得较高的原子利用效率,并以最少的步骤将中心代谢途径的小分子进行缩合。该团队对乙偶姻微生物降解途径进行分析后,利用相关反应的可逆性,通过合成生物学手段突破反应热力学限制,分别以丙酮和葡萄糖为原料构建了两条甲基乙偶姻和2-甲基-2,3-丁二醇生物合成途径,成功合成出目标化合物。
Application of Memetic Particle Swarm Optimization to Continuous Variable Global Optimization of Cost-Optimal Heat Exchanger Networks
He Qiaole,Cui Guomin,Xu Haizhu
(School of Energy and Power Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)
Heat exchanger network synthesis has been one of the most-studied problems in process synthesis. The methodologies commonly used to optimize the continuous variables are based on the deterministic methods. The continuous variable optimization is relatively easy to resolve compared with integer variable optimization,but it is diffcult to guarantee convergence to the global optimum or easy to be trapped into the local optima. Thus,in order to resolve those problems,a new memetic particle swarm optimization(MPSO) scheme was proposed,which incorporated local search techniques in the standard PSO algorithm and be combined with the improvement of the neighborhood topologies,resulting in an effcient optimization method. As a result,the confgurations of a 10SP case taken from literatures were used to confrm the MPSO performance in the continuous global optimization for the heat exchanger networks. And the reduction of the total annual cost by using the confgurations can be attributed to fne-tuning the loads of heat exchangers in the networks with MPSO.
heat exchanger network synthesis;particle swarm optimization;memetic algorithm;continuous variable global optimization;local search
1000 - 8144(2014)01 - 0037 - 09
TQ 083.4
A
2013 - 08 - 08;[修改稿日期] 2013 - 09 - 29。
何巧乐(1988—),男,浙江省宁波市人,硕士生,电话 13816970074,电邮 kingdomhe@163.com。
国家自然科学基金资助项目(51176125)。
