多杂质氢网络矩阵优化法的改进
2014-06-07贾雪雪刘桂莲
贾雪雪,刘桂莲
(西安交通大学 化学工程与技术学院, 陕西 西安 710049)
多杂质氢网络矩阵优化法的改进
贾雪雪,刘桂莲
(西安交通大学 化学工程与技术学院, 陕西 西安 710049)
针对多杂质氢网络矩阵优化法,采用浓度势的概念对其进行分析。分析结果表明,该方法中根据最大匹配流量准则确定的潜在匹配氢源和相应的潜在匹配流量,将会造成较大的浓度势损失,从而使匹配结果达不到最优。基于此采用接近流量匹配准则代替最大流量匹配准则,提出了改进的矩阵优化法,以避免浓度势排序靠前的氢源匹配给浓度势排序靠后的氢阱、减小匹配过程的浓度势损失,最终降低新氢消耗量。以改进的矩阵优化法对某石化企业的氢网络进行优化,优化结果表明,新氢消耗量比矩阵优化法的结果减少了28.11%,且所得具体匹配与数学规划法所得结果相同。
多杂质氢网络;矩阵优化法;接近流量匹配
氢气是炼油厂提高油品质量的重要原料。随着环境立法的日益严格和越来越高的石油产品质量的要求,氢气的需求量急剧增大,氢气供应日趋紧张[1]。因此,减少氢气的用量对炼油厂具有重要的意义。
目前,氢网络设计主要有图示法[2-13]和数学优化法[14-24]。Alves等[2-4]分别提出确定氢网络夹点和最小新氢耗氢量的夹点法。基于夹点法,Liu等[8-9]提出确定提纯过程最大进料流量和最优进料流量的方法。虽然图示法设计过程明确,但主要用于单杂质氢网络,对于多杂质氢网络其设计过程过于复杂[12-13]。多杂质氢网络的设计常采用数学优化法。Liao等[15-16]提出用超结构法确定提纯位置和最小新氢消耗量的方法。但超结构法属于黑箱模型,得到的解不一定是最优解。
针对多杂质氢网络,潘春晖等[24]借鉴多杂质水网络的设计提出一种浓度势综合设计方法。Liu等[25]提出矩阵演化法,可以确定最小新氢用量和具体的匹配结果。但在设计过程中,采用最大流量匹配准则选取潜在匹配氢源,这可能将过好的氢源匹配给易匹配的氢阱,导致难匹配氢阱所需要的氢源不足,增大了新氢消耗量。
本工作采用浓度势的概念对矩阵优化法进行分析,在此基础上采用接近流量匹配准则对原矩阵优化法进行改进,并用改进的矩阵优化法对多杂质氢网络进行设计优化。
1 矩阵优化法的设计步骤
1.1 问题描述
设一个氢网络系统包括m股氢源、n股氢阱和nc种杂质,每股氢源SRi的流量和杂质浓度分别为FSRi和CSRik;每股氢阱SKj的流量和进口杂质浓度分别为FSKj和CSKjk。氢阱进口杂质k的浓度要满足:
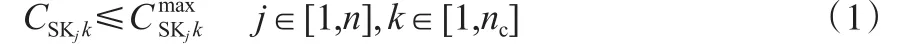
1.2 确定最大匹配流量矩阵
氢源与氢阱匹配时,当杂质k的负荷已经达到上限并且其他杂质的负荷没有达到相应的上限时,该氢源提供给该氢阱的流量为最大匹配流量Mijk,可用式(2)计算:
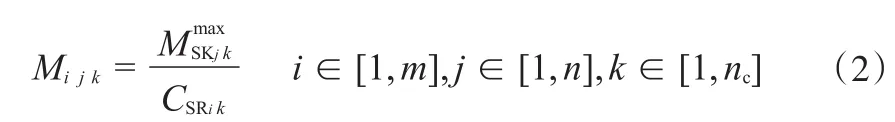
根据最小流量准则可确定一对氢源氢阱间的最大匹配流量,如式(3):
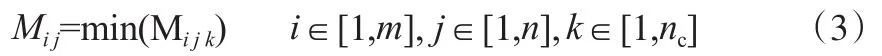
式中对应Mij的杂质为氢源SRi和氢阱SKj匹配的关键杂质(用KI表示)。将全部氢源和氢阱的最大匹配流量写入矩阵中,可得最大匹配流量矩阵(M矩阵):
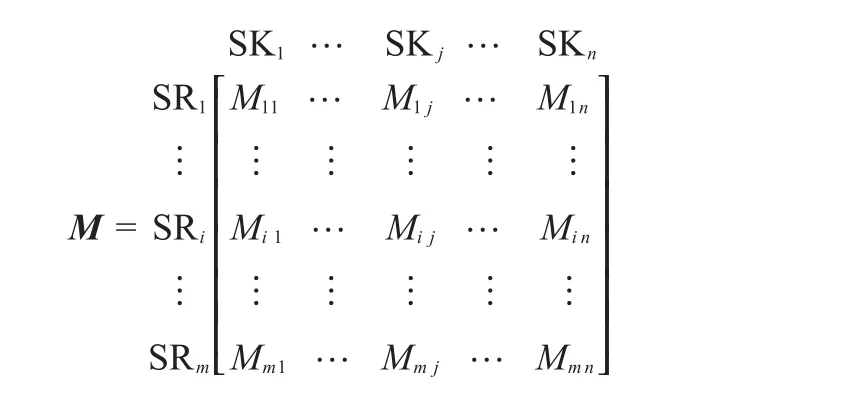
该矩阵中每一行表示一个氢源,每一列表示一个氢阱。
1.3 确定潜在匹配流量矩阵
M矩阵给出了每一股氢阱与各股氢源的最大匹配流量。氢阱在最大匹配流量与任意氢源匹配时,相应的关键杂质负荷以及浓度将达到上限,因此该氢阱不能同时与多股氢源在最大匹配流量下匹配。根据M矩阵SKj列中非零元素对应的关键杂质相同与否,可识别该氢阱的潜在匹配氢源和相应的潜在匹配流量(Pij),具体确定可分为以下两种情形。
1)非“0”元素对应相同的关键杂质。根据最大流量匹配准则选取:
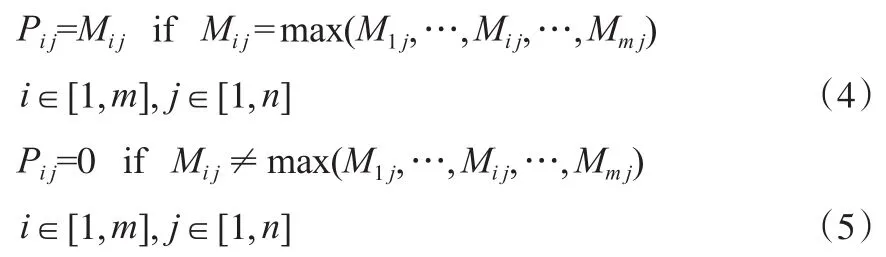
2)非“0”元素对应不同的关键杂质。此时要考虑混合互补优势,若SR1和SR2存在混合互补,其与SKj匹配的关键杂质分别为KI1j和KI2j,则两氢源的关键杂质浓度需满足式(6)和式(7):
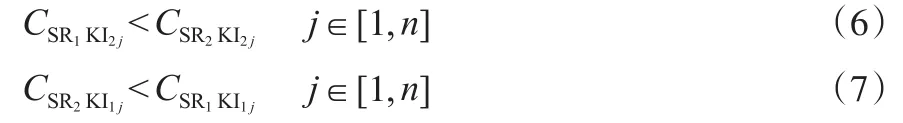
此时两氢源混合与该氢阱匹配的流量大于其中任一氢源与该氢阱的匹配流量。最大匹配量时,两种杂质同时达到氢阱进口上限时,可根据式(8)求得各氢源的混合量:
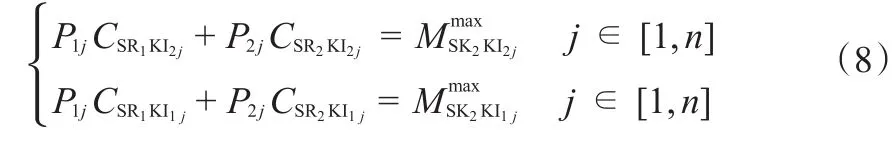
对于一个氢阱,需算出所有具有混合互补优势的氢源的最大匹配量,选择匹配流量最大的一个或一组氢源作为该氢阱的潜在匹配源,其他氢源与该氢阱的潜在匹配流量为0。若氢源之间无混合互补优势,则根据1)来确定潜在匹配源和潜在匹配流量。
将确定的潜在匹配流量写入矩阵得到潜在匹配流量矩阵(P矩阵):

1.4 确定最佳匹配流量矩阵
要得到最佳匹配流量,还需考虑氢源和氢阱的流量约束,其确定过程分为以下两种情形。
2)若Pij>FSRi,则需要根据氢阱流量和氢源回用率对潜在匹配流量进行调整。调整后潜在匹配流量变小的氢阱,则需识别其补充氢源和补充流量,最终得到各源与各阱的最佳匹配流量。
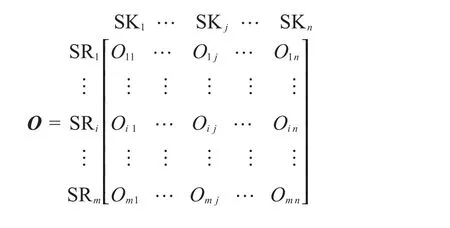
将每一股氢阱的最佳匹配流量列入矩阵中,得到最佳匹配流量矩阵(O矩阵)[25]:
2 改进的矩阵优化法
2.1 浓度势
在多杂质氢网络中,需考虑各杂质的约束,把杂质浓度低的、较好的氢源与要求高的难匹配氢阱匹配,把杂质浓度高的较差氢源匹配给要求低的氢阱,从整体上降低新氢的消耗量。但氢源中各杂质的浓度分布和氢阱中各杂质的浓度约束并无分布规律,因此很难直接分析评价氢源优劣和氢阱匹配的难易。潘春辉等[24]提出的氢网络浓度势的概念可用于评价氢源和氢阱的优劣。氢阱的浓度势(CPD)是氢阱回用各氢源的可能性的量度:
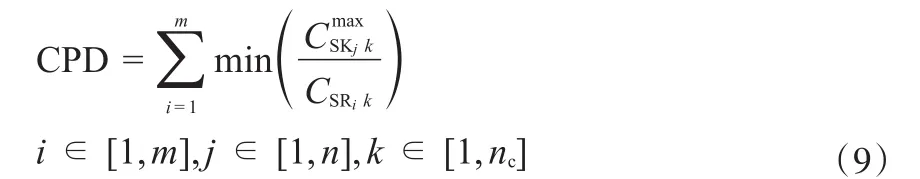
CPD的物理意义是所有氢源虚拟满足单位氢阱的量之和。氢阱的浓度势越小说明单位氢阱可以回用的氢源越少,即该氢阱越难满足,应该优先匹配。
氢源的浓度势(CPS)是氢源被各氢阱回用的总体可能性的量度:
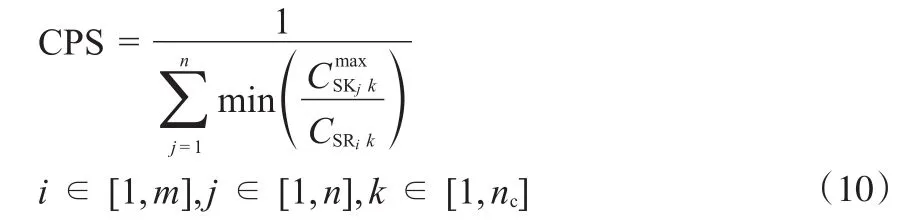
CPS的物理意义是所有氢阱被单位氢源虚拟满足的量之和。氢源的浓度势越小说明其杂质浓度越低、该氢源就越好。在氢网络匹配中应该选择浓度势排序靠前的氢源匹配浓度势靠前的氢阱,若将浓度势靠前的氢源匹配给浓度势靠后的氢阱则浓度势损失较大,浓度势排序靠前的氢源匹配浓度势靠前的氢阱则浓度势损失较小。
但在矩阵优化法中,潜在匹配源的选取采用的是最大流量匹配准则,这样可能将排序靠前的氢源选作排序靠后氢阱的潜在匹配源,造成较大的浓度势损失,导致难匹配氢源所需要的氢源不足,只能用新氢来补充,从而增大系统的新氢消耗量。
如表1所示的复杂氢网络中包括4个氢阱、7个氢源(含新氢SR0,该流股为纯氢,未列出)和4种杂质。
通过式(9)和式(10)计算,可得表1中各氢阱和氢源的浓度势及其顺序,计算结果见表2。
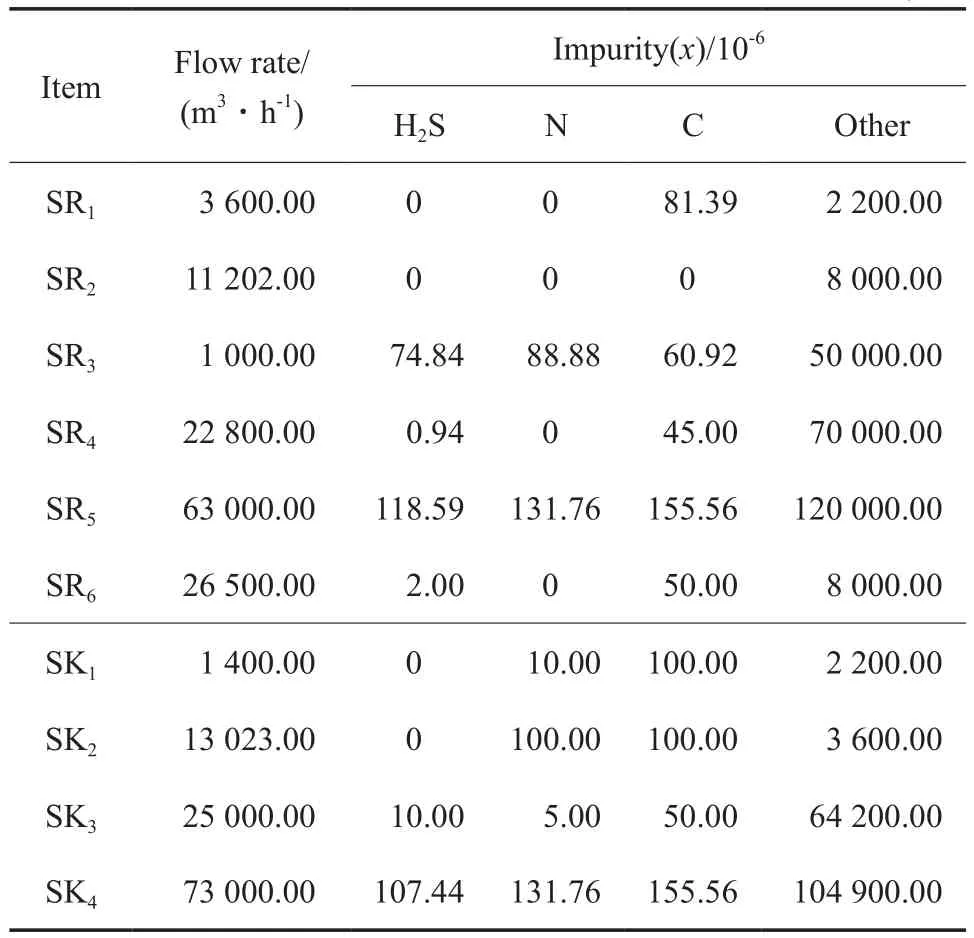
表1 氢源、氢阱的数据Table 1 Data of hydrogen sources(SRi) and hydrogen sinks(SKj)
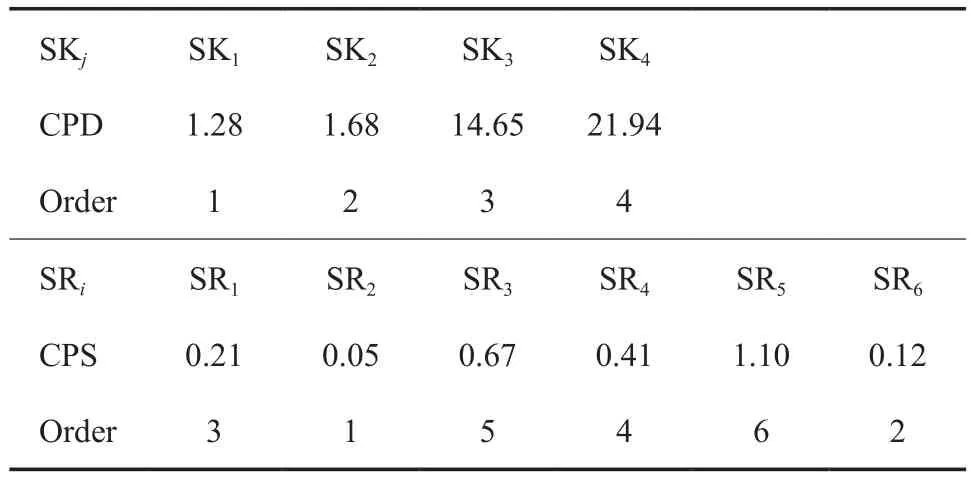
表2 氢阱和氢源的浓度势及其排序Table 2 Concentration potentials of the hydrogen sinks and hydrogen sources and their orders
根据矩阵优化法的式(2)可确定最大匹配流量矩阵:
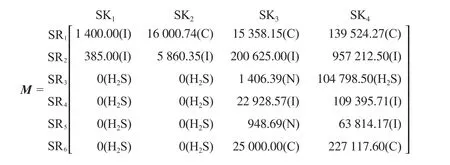
由表1中数据和混合互补准则可知,氢源与SK1和SK2匹配时不存在混合互补,所以根据式(4)和式(5)可确定二者的潜在匹配源均为SR1,相应的潜在匹配流量分别为1 400.00,16 000.74 m3/h。
对于SK3,由表1和M矩阵可知多股氢源之间存在混合互补,根据式(6)求得各组互补源之间的具体匹配数据(见表3)。其潜在匹配源选择匹配流量最大的第四组,分别是SR3(1 406.40 m3/h),SR4(2 1471.20 m3/h),SR6(3 962.40 m3/h)。
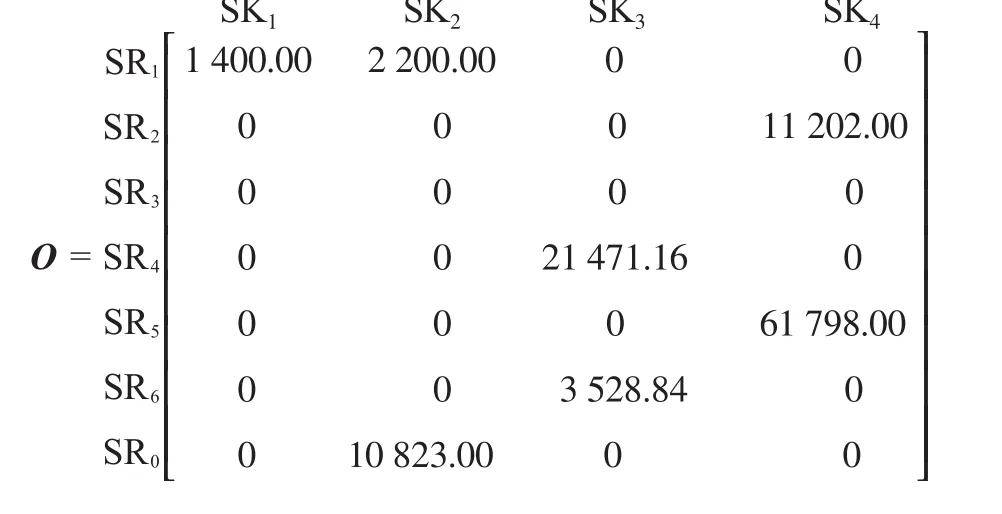
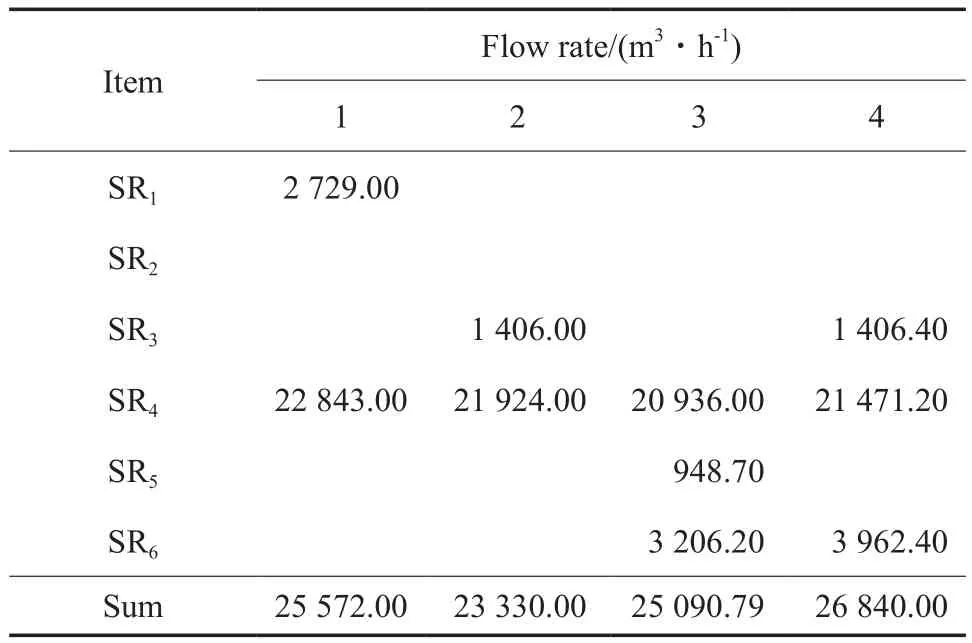
表3 可与SK3匹配的混合互补氢源及流量Table 4 Hydrogen sources which can be mixed to match SK3and their fow rates
M矩阵中各氢源与SK4匹配的关键杂质虽然不同,但各氢源不存在混合互补。按照矩阵优化法的最大流量匹配准则,应选择SR2作为其潜在匹配源。最终确定的潜在匹配流量(P矩阵)如下:
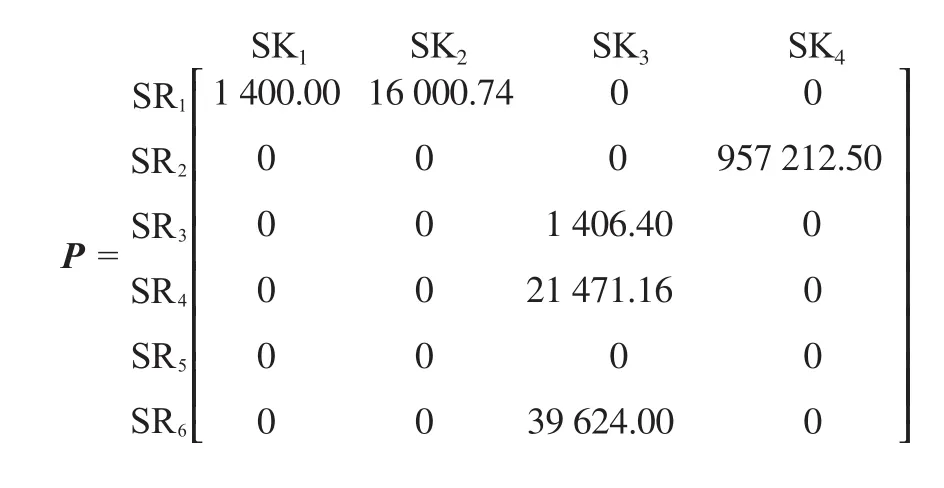
按1.4节中的方法,可确定该系统的最佳匹配流量矩阵(O矩阵)。根据O矩阵可确定该网络的新氢消耗量为10 823.00 m3/h。
由O矩阵可见,SR2完全匹配给SK4。而SK4的浓度势排序是最后一位,SR2的浓度势排序是第一位,即浓度势排序第一的氢源匹配给了浓度势排序最后一位的氢阱,浓度势损失很大。使得没有足够好的氢源与排序较前的SK2匹配,只能用新氢来补充。这将造成该氢网络的新氢消耗量偏大。
造成这种情况的原因是在潜在匹配流量和最佳匹配流量的确定中,都采用了最大流量匹配准则。这将导致排序靠前的氢源与排序靠后的氢阱匹配,存在很大的浓度势损失,从而导致整个网络的新氢消耗量增大。若能避免这种情况,则可设计出更优的氢网络。
2.2 接近流量匹配准则
要降低新氢消耗量,在确定潜在匹配氢源和最佳匹配氢源时,应使得氢源的浓度势与氢阱的浓度势排序尽可能接近。在多个氢源可与同一氢阱匹配时,匹配流量接近氢阱流量的氢源的浓度势排序最接近氢阱的浓度势排序,如表1所示的氢网络,在M矩阵中与SK4的流量最接近的是SR5和SR3。SR5与SK4的最大匹配流量小于SK4的流量,SR3的匹配流量大于SK4的流量,而且其浓度势排序最接近SK4的浓度势排序。若选取SR5作为SK4的潜在匹配源,需要消耗一定量的新氢;若选取SR3,则不需要消耗新氢。因此选取SR3与SK4匹配,而不是根据最大匹配流量准则确定的SR2。
根据上述分析,在矩阵优化法中,为减少新氢消耗量应该减小浓度势损失。这可以通过以接近流量匹配准则代替最大流量匹配准则来实现。接近流量匹配准则内容如下:在选取氢阱的潜在氢源时,若部分氢源的最大匹配流量大于该氢阱的流量,则在这些氢源中选取流量最小的一个作为该氢阱的潜在匹配源;若所有氢源与该氢阱的最大匹配流量均小于该氢阱的流量,则选取流量最大的一个氢源作为该氢阱的潜在匹配源。
对于表1所示的氢网络,根据接近流量匹配准则,SK3的潜在匹配源应为匹配流量接近的SR4,SR5,SR6的混合物,他们的匹配流量分别为20 935.82,948.69,3 206.19 m3/h。而SK4的潜在匹配源应为SR3(流量为104 798.50 m3/h),最终得到的潜在匹配流量矩阵P′为:
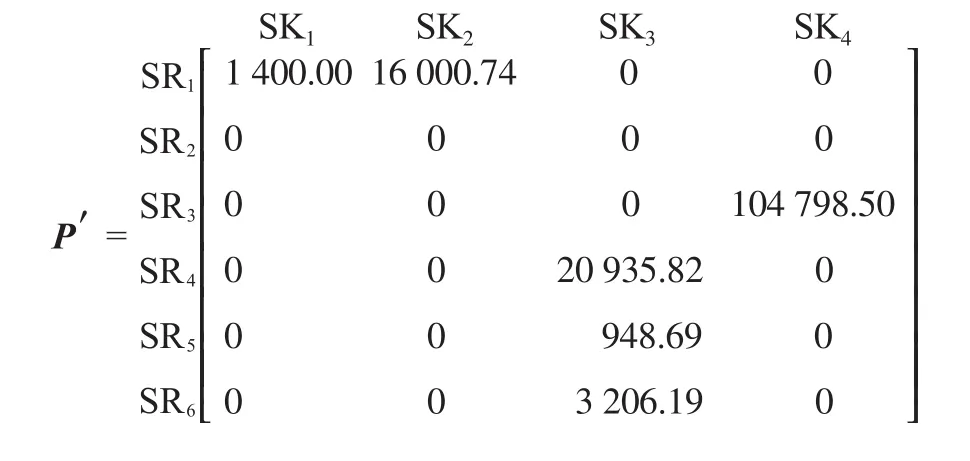
根据该潜在匹配流量矩阵,可确定最佳匹配流量矩阵O′,该网络共消耗新氢5 567.65 m3/h。

对比矩阵P′和P可以看出,浓度势排序第一的SR2没有匹配给浓度势排序最后一位的SK4,而是由浓度势排序第五的SR3与之匹配。这样在确定最佳匹配流量矩阵时就可以将浓度势排序靠前的SR2补充给浓度势同样排序靠前的SK2,减少新氢消耗量。最终根据接近流量匹配准则得到的最小新氢用量为5 567.65 m3/h,远小于根据最大流量匹配准则确定的最小新氢用量10 823.00 m3/h。而且用改进后的方法解得的结果与数学规划法所得最小新氢相同,具体匹配也很接近(见表4)。
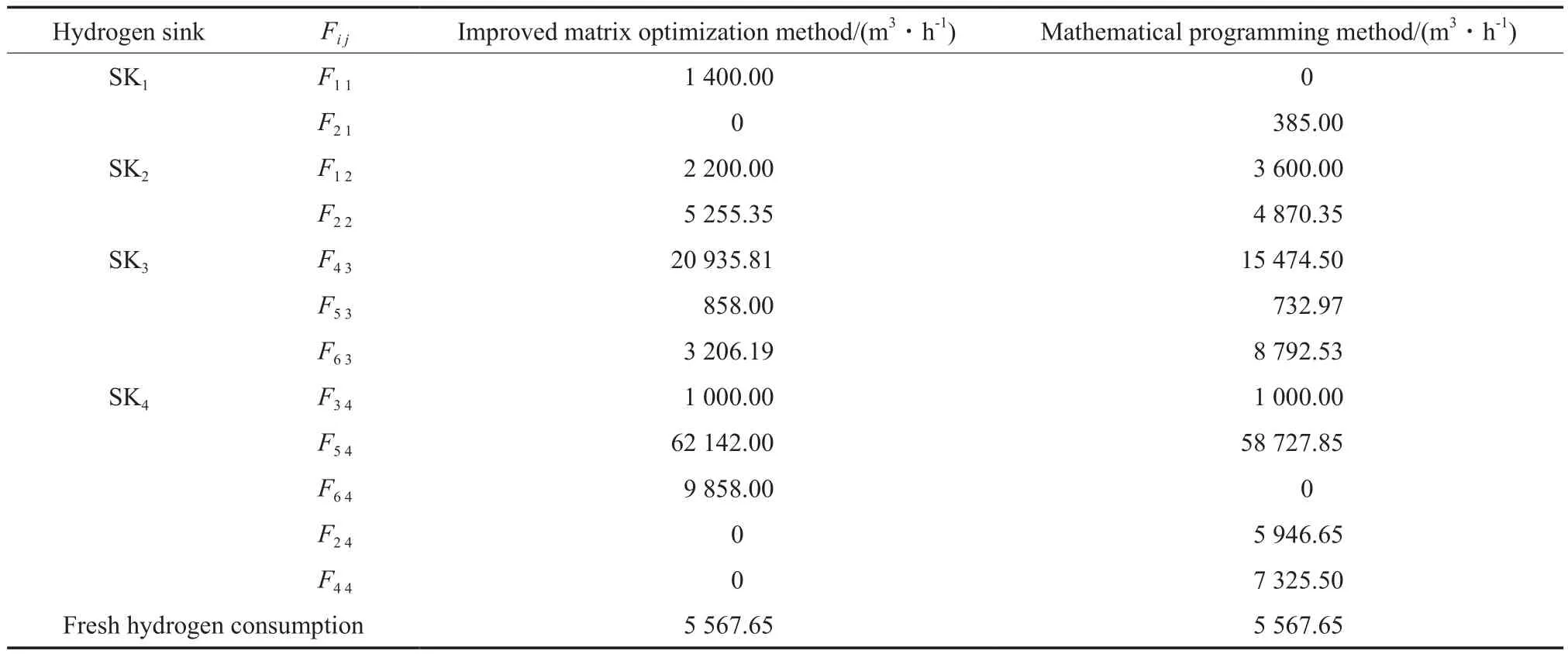
表4 改进的矩阵优化法与数学规划法优化结果的对比Table 4 Comparison between the results obtained by the improved matrix optimization method and by the mathematical programming method
3 案例分析
某石化公司的多杂质氢网络包括5股氢源(含新鲜氢气SR0)、5股氢阱和两种杂质(H2S和A),具体数据见表5。
其最大匹配流量矩阵如下(因为同一氢源与各氢阱匹配时的关键杂质相同,因此,只在最后列出关键杂质):
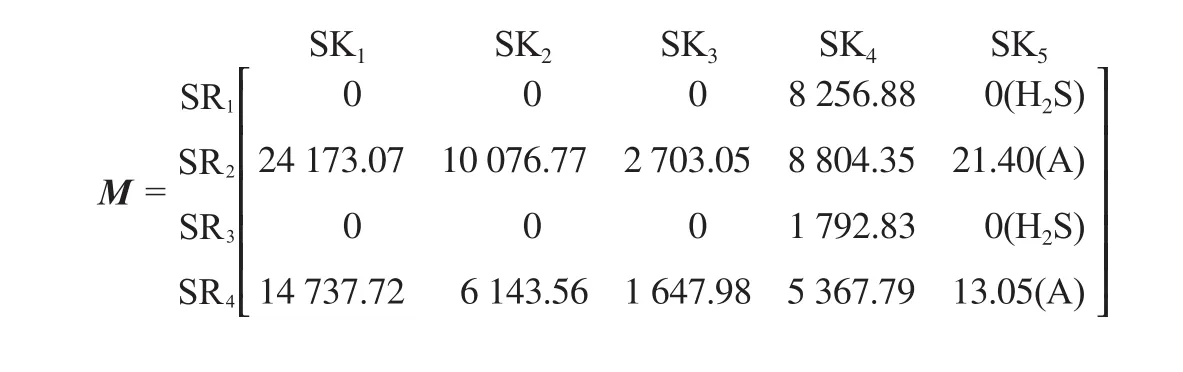
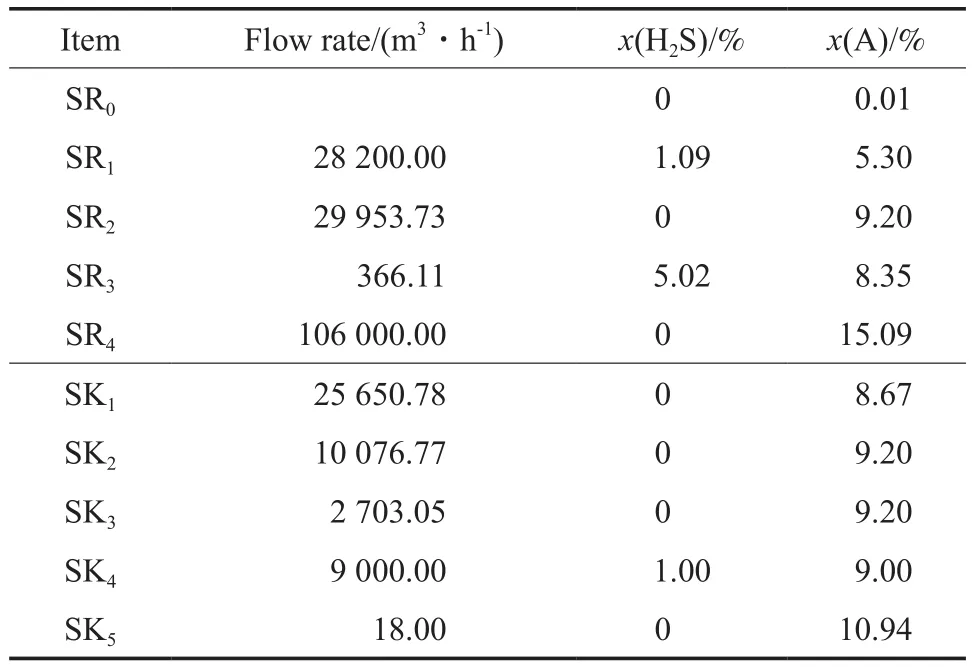
表5 某石化公司氢网络的氢源和氢阱数据[26]Table 5 Data of hydrogen sources and hydrogen sinks from a petrochemical plant[26]
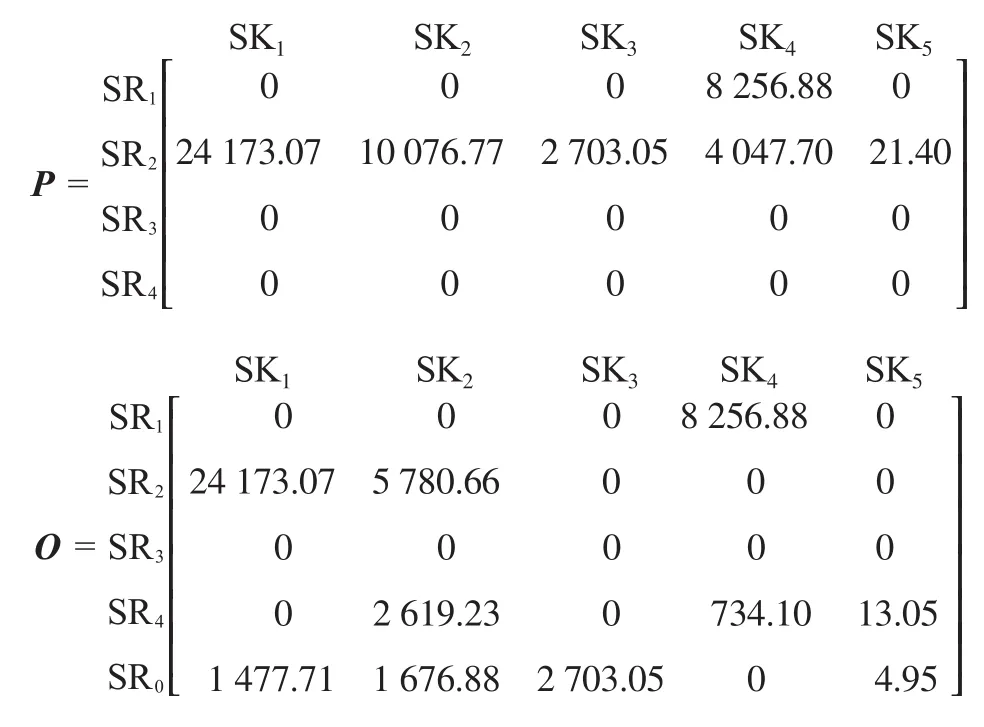
根据矩阵优化法求得的潜在匹配流量矩阵(P矩阵)和最佳匹配流量矩阵(O矩阵)如下。其中,氢阱SK4的潜在匹配源是具有混合互补优势的SR1和SR2,匹配流量分别为8 256.88,4 047.70 m3/h。根据O矩阵,可得该系统的最小新氢用量为5 862.59 m3/h。
根据式(9)和式(10)计算可得该系统中氢源和氢阱的浓度势及排序(见表6)。
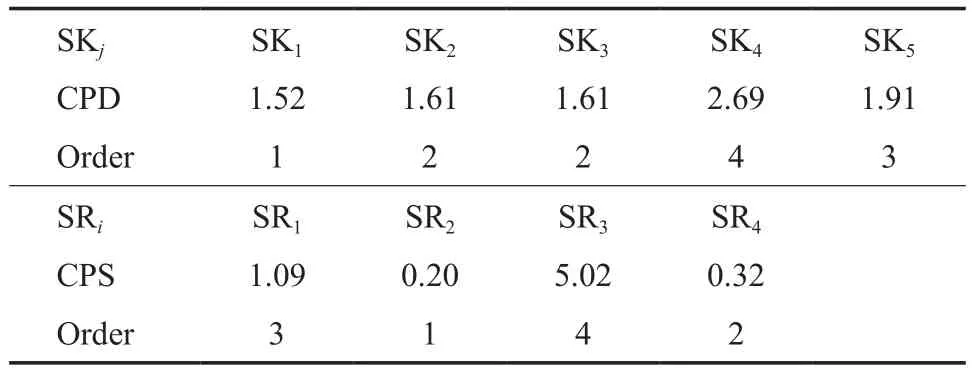
表6 氢阱和氢源的浓度势及排序Table 6 Concentration potentials of the hydrogen sinks and hydrogen sources and their orders for Table 5
若采用接近流量匹配准则,SK4的潜在匹配源应该选择同样具有混合互补优势的SR1和SR4的混合流股,它们的匹配流量分别为8 256.88,2 467.80 m3/h。最终的潜在匹配流量矩阵P′和最佳匹配流量矩阵O′如下。
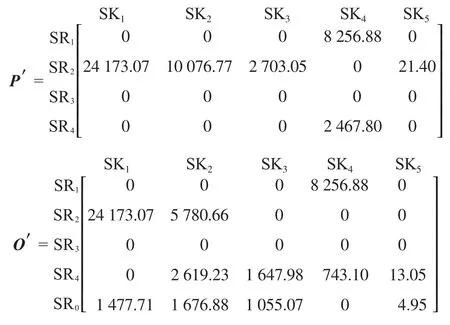
据此求得的最小新氢消耗量为4 214.60 m3/h,比矩阵优化法所得结果5 862.59 m3/h减少了28.11%。而且对于该系统,改进矩阵优化法的优化结果,无论是最小新氢消耗量还是具体的匹配结果,均与数学规划法求得的结果完全相同。
改进的矩阵优化法也可应用至考虑提纯过程的氢网络集成。对于提纯原料和提纯产品已定的氢网络,可直接用矩阵优化法进行氢网络的集成设计;若需要在氢网络集成中考虑提纯原料和提纯产品的优化,则需对矩阵优化法进行改进,以识别最优的提纯原料和提纯产品,相关研究将继续进行。
4 结论
1)矩阵优化法中根据最大流量匹配准则确定的潜在匹配氢源和相应的潜在匹配流量,可能会造成较大的浓度势损失,从而使匹配结果达不到最优。
2)提出了改进的矩阵优化法,用接近流量匹配准则代替用于确定潜在匹配流量矩阵的最大流量匹配准则。
3)改进后的矩阵优化法可避免浓度势排序靠前的氢源匹配给浓度势排序靠后的氢阱,从而获得具有较小新氢消耗量的氢网络。
4)以该改进的矩阵优化法对某石化企业的氢网络进行优化,所得结果优于原矩阵优化法,且与数学规划法所得结果相同。
符 号 说 明
CPD 氢阱的浓度势,无因次
CPS 氢源的浓度势,无因次
氢源SR1中关键杂质KI1 j的浓度(以摩尔分数计)
下角标
i 氢源,i=1, 2, …,m
j 氢阱,j=1, 2, …,n
k 杂质,k=1, 2, …,nc
KI 关键杂质
SK 氢阱
SR 氢源
上角标
max 上限
[1] Ahmad M,Zhang Nan,Jobson M. Modelling and Optimisation for Design of Hydrogen Networks for Multi-Period Operation[J]. J Clean Prod,2010,9(18):889 - 899.
[2] Alves J,Towler G. Analysis of Refnery Hydrogen Distribution Systems[J]. Ind Eng Chem Res,2002,41(23):5759 - 5769.
[3] El-Halwagi M M,Gabriel F,Harell D. Rigorous Graphical Targeting for Resource Conservation via Material Recycle/ Reuse Networks[J]. Ind Eng Chem Res,2003,42(19):4319 - 4328.
[4] Zhao Zhenhui,Liu Guilian,Feng Xiao. New Graphical Method for the Integration of Hydrogen Distribution Systems[J]. Ind Eng Chem Res,2006,45(19):6512 - 6517.
[5] 赵振辉,冯霄,刘永忠,等. 氢气网络系统的夹点分析与匹配优化[J]. 化工进展,2008,27(2):261 - 264.
[6] Agrawal V,Shenoy U. Unified Conceptual Approach to Targeting and Design of Water and Hydrogen Networks[J]. J AIChE,2006,52(3):1071 - 1082.
[7] Zhang Qiao,Feng Xiao. A Novel Graphical Method for the Integration of Hydrogen Distribution Systems[J]. Chem Eng Sci,2011,66(4):797 - 809.
[8] Liu Guilian,Li Hao,Feng Xiao,et a1. A Conceptual Method for Targeting the Maximum Purification Feed Flow Rate of Hydrogen Network[J]. Chem Eng Sci,2013,88:33 - 47.
[9] Liu Guilian,Li Hao,Feng Xiao,et a1. Novel Method for Targeting the Optimal Purification Feed Flow Rate of Hydrogen Network with Purifcation Reuse/Recycle[J]. AIChE J, 2013,59(6):1964 - 1980.
[10] 郭亚逢,郭宏新,张楠,等. 炼油厂氢气网络优化的工程设计应用[J]. 石油学报:石油加工,2012,28(1):107 - 114.
[11] 张清新,杨兴,于思江,等. 炼厂氢气网络的夹点分析及优化[J]. 炼油技术与工程,2012,42(11):1 - 5.
[12] Wang Bin,Feng Xiao,Khim H. A Novel Graphical Procedure Based on Ternary Diagram for Minimizing Refnery Consumption of Fresh Hydrogen[J]. J Clean Prod,2012,37:202 - 210.
[13] Zhang Qiao,Feng Xiao,Khim H. Evolutionary Graphical Approach for Simultaneous Targeting and Design of Resource Conservation Networks with Multiple Contaminants[J]. Ind Eng Chem Res,2013,52(3):1309 - 1321.
[14] Liao Zuwei,Rong Gang,Wang Jingdai,et a1. Rigorous Algorithmic Targeting Methods for Hydrogen Networks:Ⅰ. Systems with No Hydrogen Purifcation[J]. Chem Eng Sci,2011,66(5):813 - 820.
[15] Liao Zuwei,Rong Gang,Wang Jingdai,et a1. Rigorous Algorithmic Targeting Methods for Hydrogen Networks:Ⅱ. Systems with One Hydrogen Purifcation Unit[J]. Chem Eng Sci,2011,66(5):821 - 833.
[16] Zhou Li,Liao Zuwei,Wang Jingdai,et a1.Optimal Design of Sustainable Hydrogen Networks[J]. Int J Hydrogen Energy,2013,38(7):2937 - 2950.
[17] Zhou Li,Liao Zuwei,Wang Jingdai,et a1. Hydrogen Sulfide Removal Process Embedded Optimization of Hydrogen Network[J]. Int J Hydrogen Energy,2012,37(23):18163 - 18174.
[18] 丁晔,冯霄,刘桂莲,等. 多杂质质量交换网络赤字率方法的改进[J]. 华东理工大学学报:自然科学版,2009,35(4):521 - 524.
[19] 丁晔,冯霄. 多杂质氢系统网络设计[J]. 西安交通大学学报,2010,44(8):127 - 131.
[20] Hallale N,Liu Fang. Refinery Hydrogen Management for Clean Fuels Production[J]. Adv Environ Res,2001,6(1):81 - 98.
[21] 张毅,阳永荣,刘军,等. 炼油厂氢气网络集成管理[J].石油学报:石油加工,2004,20(1):58 - 62.
[22] 刘永忠,张超,赵振辉,等. 基于超结构方法的氢网络系统优化[J]. 华北电力大学学报,2007,34(2):24 - 26.
[23] 陈诚,薛焘,游晓艳,等. 炼油厂氢气分配系统超结构优化方法研究进展[J]. 广东化工,2011,38(9):279 - 279,274.
[24] 潘春晖,王焕云,刘凤茹,等. 多杂质氢网络的浓度势综合设计方法[J]. 石油化工,2012,41(12):1401 - 1406.
[25] Liu Guilian,Tang Mingyuan,Feng Xiao,et al. Evolutionary Design Methodology for Resource Allocation Networks with Multiple Impurities[J]. Ind Eng Chem Res,2011,50(5):2959 - 2970.
[26] 刘桂莲,周华,温光林. 考虑热量和压力功影响的氢网络扩展矩阵法[J]. 华东理工大学学报:自然科学版,2013,39(2):143 - 146.
(编辑 李治泉)
Improvement of Matrix Optimization Method for Hydrogen Networks with Multiple Impurities
Jia Xuexue,Liu Guilian
(School of Chemical Engineering and Technology,Xi’an Jiaotong University,Xi’an Shaanxi 710049,China)
The present matrix optimization method for hydrogen networks with multiple impurities was analyzed according to the concept of concentration potential. The results showed that potential match hydrogen source and corresponding potential match flow rate identified according to the maximum match flow rate principle might lead to a large loss of the concentration potential. Based on this,an improved matrix optimization method was proposed. The near flow rate principle was presented to substitute the maximum fow rate principle to identify the potential match fow rate. This improved matrix optimization method can avoid the hydrogen sources with high ranking order on the concentration potential to be matched with the hydrogen sinks with low ranking order and reduce the loss of the concentration potential. Hence,the fresh hydrogen consumption of hydrogen networks can be decreased. Based on the improved matrix optimization method, the fresh hydrogen consumption can be reduced by 28.11%. And the results are the same as that obtained by mathematical programming method.
hydrogen networks with multiple impurities;matrix optimization method;near fow rate principle
1000 - 8144(2014)01 - 0030 - 07
TQ 018
A
2013 - 07 - 13;[修改稿日期] 2013 - 09 - 18。
贾雪雪(1989—),女,山西省襄汾县人,硕士生。联系人:刘桂莲,电话 029 - 82664376, 电邮 guilianliui@mail. xjtu.edu.cn。
国家自然科学基金项目(21276205;20936004)。
