基于遗传算法的化工园区环境风险源优化模式研究

汪林 朱京海

基于遗传算法的化工园区环境风险源优化模式研究

汪林 朱京海

通过优化区域规划方案可以从根本上避免环境风险，以大连某化工园区为案例，建立了基于遗传算法的化工园区环境风险源优化模型，从周边敏感点情况、风频、事故发生频率、毒性物质的毒性级别及其储存量、临近度因子等方面对区域内环境风险源位置进行优化，模型运行结果得到该区域环境风险源位置相对坐标，从而尽量规避园区环境风险，进一步丰富了规划环境评价技术方法。

环境风险；遗传算法；优化

战略环境评价(Strategic Environmental Assessment，SEA)应关注在规划和政策形成阶段，通过调整规划方案来最大限度地回避环境风险；而区域环境风险的大小受敏感点人口密度、风频等多种因素影响[1]；可以将多种规划方案的环境风险进行比较，从而选择一个风险最小的方案，即寻找最优解。

1 方法选择

遗传算法是解决搜索问题的优秀算法，其适应度函数不受连续、可微等条件的约束，定义域可任意设定，能够满足资源配置的多样性要求。遗传算法用于优化问题时直接作用于目标函数，基本上不需要其他辅助信息就可以从整个种群中选择生命力强的个体产生新的种群，对搜索空间中的多个解进行评估[2-3]，它同时处理群体中的多个个体，即从初始阶段使用多个搜索点，减少了陷入局部最优解的风险，同时算法本身易于实现并行化。

基于以上优点，作为以函数优化为主的规划配置问题完全可以应用遗传算法来进行计算。这里以大连某化工园区为例，建立基于遗传算法的风险源优化模型，以期减小因规划不合理造成的环境风险。

2 模型建立

拟建的模型以遗传算法为基础，研究在园区在每个拟建企业中，环境风险源即有毒物质储罐等风险源如何通过优化其具体布局来减小区域环境风险。

由于突发性风险的大小与风险源的危险程度、与受体的相对位置关系以及气象和地理条件都有关系，因此在对潜在突发性风险源进行优化时，这些方面都应考虑。

筛选出6个因子来优化该区域的风险：敏感点情况、风频、事故发生频率、毒性物质的毒性级别及其储存量和临近度因子[4-6]。区域内环境风险源的优化目标可以用到环境敏感点的距离和各个风险源的危险系数乘积来表示，优化的目标是确立风险源的位置，使得目标函数达到最小值即区域环境风险达到最小，如式(1)所示：

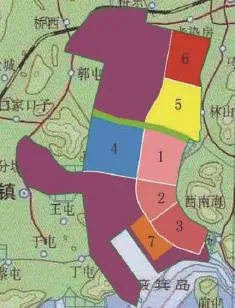
图1 像素约束

式中：Ni为第i个敏感点的人口数量，人；Pji为j风险源相对i敏感点的风频；Rj为突发性风险事故发生的频率；Bj为j风险源风险性物质的毒性级别；xj、yj为第j块用地的内风险源位置坐标；ai、bi为第i个敏感点的中心点坐标。

其实，在式(1)里面Pji，Rj，Bj等参数，均可以用一个参数来表征，这个参数就是风险值R。环境风险指突发性事故对环境(或健康)的危害程度，用风险值(R)表征。 风险值(R)指事故发生概率(P)与事故造成的环境(或健康)后果(C)的乘积，在对环境风险值R的统计中，已经综合考虑进了风频及毒性级别等因素，因此，可用环境风险值R代替公式(1)中的Pji，Rj，Bj等参数的乘积，上述目标函数简化为模型(2)：

式中：Ni为第i个敏感点的人口数量，人；Rj为第j块用地的环境风险值；xj、yj为第j块用地的内风险源位置坐标；ai、bi为第i个敏感点的中心点坐标。

约束条件可以用图上的像素控制，所以模型(2)的约束条件为xj、yj必须在地块j范围内。这里可以通过不同颜色的像素进行控制，每个地块在图上都有不同的颜色，每个颜色都是由三原色构成，每个像素(图上任一点)都是由3个字节构成，每个字节代表1个颜色。可以通过随机产生的坐标值判断该坐标点对应的3个字节构成的颜色是否与图1中给出的每个地块颜色相同，从而判断该随机坐标是否处于其所属企业范围内。

3 程序设置

算法采用C#语言编程实现[7-9]。

①编码和解码

编码是应用遗传算法首先要解决的关键问题。采用二进制编码方式，定义一个长度为1h20的染色体。

②初始种群的产生

按照随机生成的方法产生初始染色体，这里选择的种群大小为50。

步骤1：设定随机函数rand()%10<5，若为真则相应的基因设置为1，否则为0。

步骤2：整条染色体将被初始化。

步骤3：按照同样的规则依次将种群内的其他染色体初始化。

步骤4：重复上述步骤得到初始种群的所有个体。

③适应度函数的设计

本文的适应度函数即为目标函数。

④产生新种群

根据适应度值的大小从种群中选择优良的染色体，使它们成为新一代种群。在选择操作上，本文通过赌轮选择法选择个体。在该方法中各个个体的选择概率与其适应度成正比。其执行步骤如下：

步骤3：最后在使用模拟赌轮选择操作，即产生0到1之间的随机数，来确定各个个体被选中的次数。

⑤交叉操作

交叉是遗传算法的最重要操作，交叉操作主要用于组合生成新的个体，在解空间中进行有效搜索，同时降低对有效模式的破坏概率。在本文中设计的交叉概率为1，这样能够完全保证子代对父代的良好特性。交叉操作步骤如下：

步骤1：利用随机函数确定交叉点；

步骤2：确定第一个父代个体2个交叉点之间的基因片段在第二个父代中的相应位置；

步骤3：依次按顺序交叉。

⑥变异操作

对新种群按照变异概率对选中染色体执行变异操作，使其避免陷入局部最优解，防止早熟收敛。因此变异概率应尽量地小，本文采用的变异概率为0.002。变异操作的具体步骤如下：

步骤1：随机生成0～1之间的数字，与变异概率作比较。如大于变异概率则转到步骤2，否则终止变异操作。

步骤2：从染色体中随机选择两个操作位置。

步骤3：对选中的位置做互换变异操作。

重复选择、交叉和变异操作，产生新一代种群，直至选择出最佳个体，终止操作。

4 参数设置

在具体求解时，需要确定目标函数中的各个参数。首先确定Ni，即从1~i各个敏感点的人口数，见表1，同时确定各个敏感点坐标的(ai，bi)。

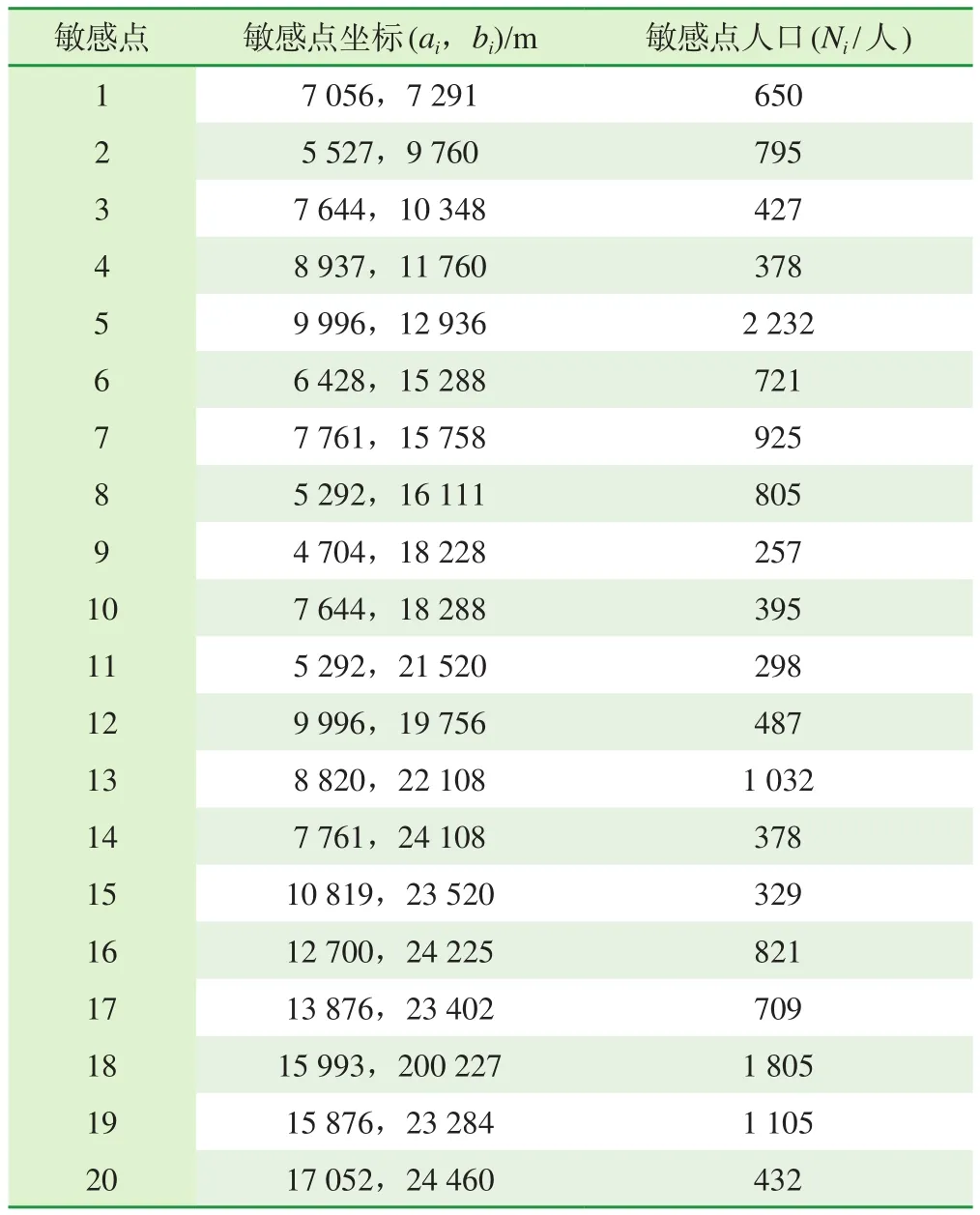
表1 园区周边主要敏感点位置及坐标

之后，确定目标函数中的Rj，即从1~j各个化工产业类型所代表的环境风险值，见表2。

表2 各拟规划工业用对应的环境风险值

5 优化计算结果

优化计算结果见表3。表3中列出了环境风险源中心坐标，也就是说在进行企业平面布置时，应该尽量把风险源按照表中优化计算结果进行布置，才能尽量减小对周围敏感区域造成的环境风险。

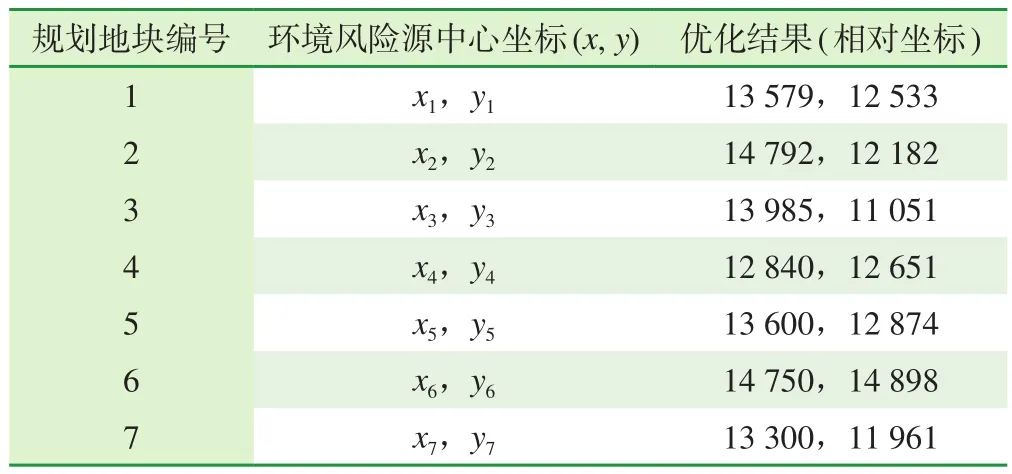
表3 拟规划地块的中心点坐标

6 结论

本研究创新性地将遗传算法引入SEA，建立环境风险优化模型，通过遗传算法的强大搜索功能，对区域环境风险源布局方式进行逐一组合，模型运行结果找到了园区7个风险源的最佳位置坐标，最大限度地使风险源布局保障人群健康及规避环境风险，从而为化工园区SEA实践提供更多的技术支持。

[1] 钟政林, 曾光明, 杨春平. 环境风险评价研究进展[J]. 环境科学进展, 1996, 4(6): 17-21.

[2] 张文修, 梁怡. 遗传算法的数学基础[M]. 西安:西安交通大学出版社, 2004.

[3] 房育栋, 郝建忠, 余英林, 等.遗传算法及其在TSP中的应用[J]. 华南理工大学学报, 1994, 22(3): 124-127.

[4] 王志霞. 区域规划环境风险评价理论、方法与实践[D]. 上海: 同济大学, 2007.

[5] 彭王敏子. 规划环评中环境风险评价方法的研究与探讨[D]. 厦门: 厦门大学, 2009.

[6] 彭王敏子. 不同应用层次的环境风险评价技术方法的研究进展[J]. 环境科学与管理, 2009, 34(7): 170-173.

[7] 陈国良, 王煦法, 庄镇泉, 等. 遗传算法及其应用[M]. 北京: 人民邮电出版社, 1996.

[8] 周明, 孙树栋. 遗传算法原理及其应用[M]. 北京: 国防工业出版社, 1999.

[9] 戴晓明, 邹润民, 冯瑞, 等. 混合并行遗传算法求解TSP问题[J]. 电子与信息学报, 2002, 24(10): 1424-1427.

X820.4

A

2095-6444(2014)05-0045-03

2014-08-10

国家自然科学基金(40801228)

朱京海，辽宁省环保厅厅长，研究员，博士生导师；汪林，大连大学环境与化学工程学院高级工程师。