Klein-Gordon-Schrödinger方程组的精确解
2014-06-07张金良
李 伟,张金良
(河南科技大学数学与统计学院,河南 洛阳 471023)
Klein-Gordon-Schrödinger方程组的精确解
李 伟,张金良
(河南科技大学数学与统计学院,河南 洛阳 471023)
利用(G′/G)-展开法求出了Klein-Gordon-Schrödinger方程组含参数的双曲函数形式孤波解及三角函数形式周期波解。文献中用齐次平衡原则与F展开法得到的孤波解与三角函数解是本文所得精确解的特殊情况。此外,结合刘氏定理又得出一种类型的孤波解——扭钟型孤波解。
Klein-Gordon-Schrödinger方程组;(G′/G)-展开法;刘氏定理;孤波解;周期波解;扭钟型解
0 引言
本文所讨论的Klein-Gordon-Schrödinger(KGS)方程组,是应用科学中出现的重要的非线性发展方程组,它在现代物理中具有十分重要的作用。其一般形式为:
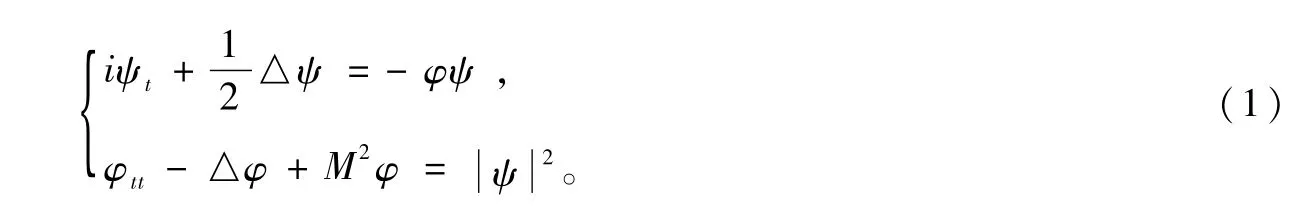
该方程组描述了一个保守的复原子核场ψ与一个实中性介子场φ相互作用的古典Yukaua模型[1],这两个场是标量场。M是介子的质量,△是拉普拉斯算子。文献[2]用齐次平衡方法得出了该方程组的孤波解;文献[3-6]用F展开法得出了方程组(1)的周期波解。本文利用(G′/G)-展开法[7-10]求出了方程组(1)的含参数的行波解,当参数取特殊值时,可得到文献[2-5]中的一些孤波解与三角函数解。此外,结合刘氏定理[11]由钟型解得出扭钟型解。扭钟型解在文献[2-6]中没有出现。
1 KGS方程组的精确解
由于ψ(x,t)是一个复函数,设
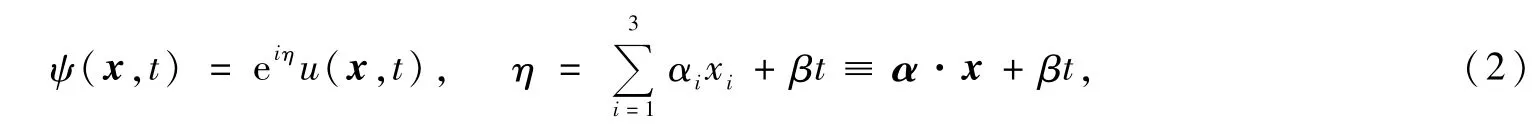
其中,x=(x1,x2,x3)∈ℝ3;t∈ℝ;α≡(α1,α2,α3)∈ℝ3。
将式(2)代入方程组(1),得方程组如下:

设方程组(3)的行波解为:

其中,k、α是待定常向量。将式(4)代入方程组(3),可得常微分方程组:




2 结论
本文利用(G′/G)-展开法求出了Klein-Gordon-Schrödinger方程组的含参数的两种类型的行波解。适当选择参数,由这两种类型的行波解可得到文献[2-5]中用齐次平衡方法与F展开法得出的孤波解与三角函数周期波解。由此说明(G′/G)-展开法可得出比文献中更为丰富的孤波解与三角函数解。此外,将(G′/G)-展开法与刘氏定理相结合,易得到扭钟型孤波解及正切正割型三角函数解,进一步丰富了由(G′/G)-展开法求得的精确解。表明本文所用方法是获得非线性方程孤波解与三角函数解的一种高效、直接、简明的方法。
致谢:本文得到王明亮教授的指导,在此表示衷心感谢。
[1] Fukuda I,Tsutsum i M.On Coupled Klein-Gordon-Schrödinger Equations[J].JMath Appl,1978,66:358-378.
[2] Xia JN,Han S X,Wang M L.The Exact Solitary Wave Solution for the Klein-Gordon-Schrödinger Equations[J].Appl Math Mech,2002,23:58-64.
[3] Wang M L,Zhou Y B.The Periodic Wave Solutions for the Klein-Gordon-Schrödinger Equations[J].Phys Lett A,2003,318:84-92.
[4] Li X Y,Yang S,Wang M L.The Periodic Wave Solutions for the(3+1)-dimensional Klein-Gordon-Schrödinger Equations[J].Chaos Solitons Fractals,2005,25:629-636.
[5] Li X Y,Li X Z,Wang M L.Extended F-expansion Method and Periodic Wave Solutions for Klein-Gordon-Schrödinger Equations[J].Commun Theor Phys,2006,45:9-14.
[6] Darwish A,Fan E G.A Series of New Explicit Exact Solutions for the Coupled K lein-Gordon-Schrödinger Equations[J]. Chaos Solitons Fractals,2004,20:609-617.
[7] Wang M L,Li X Z,Zhang J L.The(G′/G)-expansion Method and Traveling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics[J].Phys Lett A,2008,372:417-423.
[8] 李向正,张卫国,原三领.(G′/G)展开法的简化及Nagumo方程的有界行波解[J].河南科技大学学报:自然科学版,2010,31(6):78-81.
[9] 李保安,李灵晓.简化变形Ostrovsky方程的精确解[J].河南科技大学学报:自然科学版,2014,35(2):82-85.
[10] 李向正.Sawada-Kotera方程的两类尖孤立波解[J].河南科技大学学报:自然科学版,2014,35(2):78-81.
[11] Liu C P.The Relation Between the Kink-type Solution and the Kink-bell-type Solution of Nonlinear Evolution Equations[J].Phys Lett A,2003,312:41-48.
[12] Wang M L.Solitary Wave Solutions for Variant Boussinesq Equations[J].Phys Lett A,1995,199:169-172.
[13] Wang M L.Exact Solutions for a Compound KdV-Burgers Equation[J].Phys Lett A,1996,213:279-287.
O175.2
A
1672-6871(2014)06-0084-04
国家自然科学基金项目(11171227);河南省科技攻关基金项目(132102310309)
李 伟(1964-),女,河南偃师人,副教授,硕士,主要研究方向为非线性数学物理方程.
2014-05-29
