低频强磁场发生线圈电感系数的计算与测试

2014-06-07黄刘宏李跃波丁世敬

河南科技大学学报(自然科学版) 2014年6期

关键词：自感互感强磁场

黄刘宏，李跃波，丁世敬，杨杰，刘锋

（总参工程兵科研三所，河南洛阳 471023）

低频强磁场发生线圈电感系数的计算与测试

黄刘宏，李跃波，丁世敬，杨杰，刘锋

（总参工程兵科研三所，河南洛阳 471023）

针对低频强磁场模拟试验设备中的磁场发生线圈为一大型疏绕螺线圈组，其电感系数难以利用现有公式计算的实际问题，采用理论公式计算该螺线圈组的自感，采用ANSYS有限元仿真计算其有效电感系数（包括自感和互感）。同时，将数值计算结果与实体螺线圈有效电感的测试数据进行了对比分析。研究结果已应用于低频强磁场模拟试验室磁场发生线圈的设计和其电阻、电器、电容脉冲电流激励电路参数的确定。

低频；强磁场；疏绕螺线圈；电感系数；数值模拟

0 引言

低频强磁场模拟试验系统采用高压高能脉冲源对大型螺线圈放电，从而在螺线圈内部产生低频低阻抗的强磁场，该系统为模拟地面核爆炸强磁场的破坏效应及防护技术研究提供了性能先进的试验手段。该系统的磁场产生装置为一大型疏绕的螺线圈组，由相同尺寸、均匀间隔25 cm的4个螺线圈组成，每个螺线圈均由直径10 mm、壁厚1 mm的紫铜管以1匝／m绕制成直径6 m、长度10 m的空间螺旋线状。

螺线圈组所在的脉冲电流激励电路由高压电容、螺线圈和回路电阻组成，为典型的电阻、电感、电容（RLC）串联放电回路，线圈组的电感系数是影响整个RLC放电回路能否工作在过阻尼状态的关键参数，是回路高压电容和电阻取值选择的重要依据，因此，准确地计算螺线圈组的电感系数（包括自感和互感）至关重要。但目前对螺线圈电感系数的研究关注点集中在常见的理想化单层或多层密绕螺线圈模型［1］，对疏绕螺线圈只有少量侧重于自感计算［2－5］的文献，并无可适用的疏绕线圈组互感计算方法。而本文的研究对象是空间等距平行排列的4个疏绕线圈，线圈间的互感对整个线圈组的有效电感影响很大，如果只是简单地等效为单层密绕螺线圈，或按多个单匝线圈电感串并联来估算，存在着准确性和误差未知的问题，对低频强磁场模拟系统回路高压电容和电阻的取值会带来极大的不确定性，直接影响系统指标的实现。为解决上述问题，本文采用理论公式近似计算与Ansys有限元仿真相结合的方法，对实体模型的电感系数进行了计算，同时与试验测试数据进行了对比分析。

1 理论计算

下面给出单个疏绕螺线圈自感的理论近似计算公式，需要说明的是其不适用于计算多线圈间的互感。

疏绕螺线圈结构如图1所示，螺线圈半径R，导线自身半径r，螺线圈的螺距h，管长l。取螺线圈轴线方向为z轴。对于由圆形截面导线组成的任意回路，外自感Le可证明为［6］：

式中，x为导线的中心线上任意两个线元d l1和d l2之间的距离。积分遍及中心线上所有满足条件x＞r／2的线元对。在螺线圈导线的中心线上任取两个线元d l1和d l2，从螺线圈在XY平面上的横截面图（见图1b）可以看出：d l1·d l2＝d z1·d z2＋d S1·d S2。式中，d Si为d li在XY平面上的分矢量。对螺距不变的螺线圈，有常量tanα＝d z／d S＝h／（2πR）。

图1 疏绕螺线圈结构

由图1可知：

式中，φ可取值为2π（z2－z1）／h（可能多取了2π的整数倍，但不影响cosφ的值）。故得

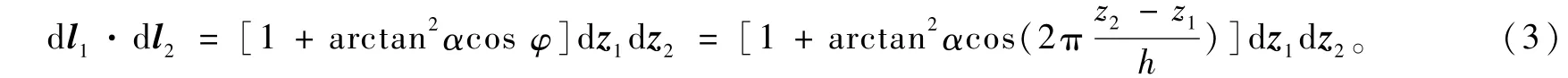
另外，由图1可知：

蒙特卡洛方法求积分具有与积分重数无关的优点，但收敛速度较慢，计算误差与成正比。整个数值积分采用Fortran语言编程，经试算，随机点数N取105能兼顾计算精度和计算效率。按照前述螺线圈的尺寸参数，代入式（6）和式（8），经计算得单个螺线圈的自感为412.9μH，若将4个螺线圈串联的情形等效为单个螺线圈，则自感为4 822.3μH。对于线圈间的互感则无法利用此公式计算。

2 仿真分析

电感系数涉及到线圈自感和4个线圈间的互感共计4个参数，因此采用ANSYS编程时，要分4个程序分别仿真计算。每个仿真程序均采用SOLID 96单元进行静磁场分析，源电流采用SOURCE 36虚单元。

在建立空间螺线圈几何模型时采用分段圆弧的方式，即单匝线圈（一个螺旋）设定由数个圆弧段组成，经多次试算，在综合考虑计算精度和效率后设定为20。由于线圈模型具有对称性，为减小计算量提高计算效率，可仅计算全模型的1／4。近场区和远场区采用不同的网格划分尺寸，以兼顾计算精度和计算效率。经多次试算和比较，设定近场区网格尺寸为150 mm，远场区网格尺寸为800 mm。图2为建立的1／4计算域网格剖分图，为单个螺线圈模型以计算其自感；图3为两个螺线圈电流模型，以推算线圈间的互感。

图2 单个螺线圈计算域网格图

图3 两个螺线圈电流模型

电感利用磁场能量公式E＝I2L／2推算，该方法比基于磁通量的方法准确度稍高。具体操作是通过ANSYS后处理计算总磁能E，再根据设定的电流I＝104A计算（有效）电感L。

对于单个螺线圈，算得的有效电感就是其自感，经计算得单个螺线圈的自感L11（＝L22＝L33＝L44）＝309.317 66μH。对于两个螺线圈情形，算得的为两个线圈的有效电感。程序中设定每个线圈中均通有电流104A，因此，如果认为两线圈为串联，则依据串联的有效电感公式L＝L1＋L2＋2M推算互感；若认为两线圈为并联，则依据并联的有效电感公式L＝（L1L2－M2）／（L1＋L2－2M）推算互感，但此时代入磁场能量公式中的电流I需为2×104A。显然，对于两个线圈的情形，并联有效互感为串联有效互感的1／4，按照类似的关系，可据此推算多个线圈并联接入时的有效电感。

根据接入两个线圈时ANSYS仿真结果，利用磁能公式可推算线圈1与线圈2的有效电感L12＝1 148.727 04μH，线圈1与线圈3的有效电感L13＝1 117.392 21μH，线圈1与线圈4的有效电感L14＝1 135.874 00μH。按照串联有效电感公式可计算两两螺线圈间的互感，其结果以电感矩形的形式列于表1中（单位为μH）。分析表1的结果可以看出：①螺线圈之间的互感大小关系为M12＞M14＞M13，这与线圈间的远近程度（线圈1与2的距离≤线圈1与4的距离＜线圈1与3的距离）所体现的规律一致。②互感和自感相差并不大。进一步地计算线圈间的耦合因数k，有k12＝0.856 8，k13＝0.806 3，k14＝0.836 1，表明线圈间磁通彼此交链的百分比在80%～86%。这说明，尽管与密绕相比，本线圈组绕制相对松散，两两线圈间距有25 cm和50 cm，但从这种平行套接的绕制效果来看，互感比较大。

考虑到试验室线圈组可采用不同的线圈接入类型（分串联和并联两种）和数量，可利用上述已知的自感和互感，计算不同接入情形下的有效电感值，结果见表2。从表2中可以看出：通过灵活地调整接入线圈的数量和串并形式，其有效电感变化范围为271.4～4 342.0μH（尽管不是连续变化），这也为通过改变电感从而调整脉冲磁场上升时间及频谱提供了可能。

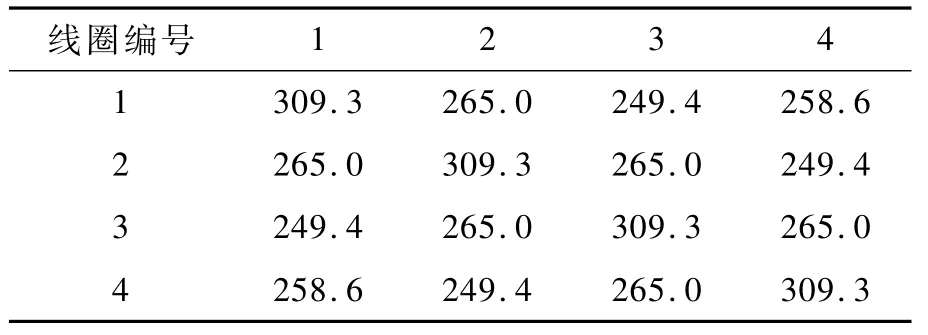
表1 疏绕螺线圈电感矩阵 μH

表2中并联情形利用其与串联情形时的数值关系计算，为验证其正确性，采用ANSYS对4个线圈并联接入时的有效电感进行了仿真，结果为271.191 33μH，显然与表2中依数值计算关系算得的271.4μH很接近。从表2中两种接入类型的计算结果可以看出：由于线圈间的耦合系数较大，单个线圈产生的磁通大部分都能彼此交链，互感已不可忽略，因此2个、3个或4个线圈在串联时接入的有效电感会比单个线圈自感的2倍、3倍或4倍还大；而并联接入时，由于互感的补充，仅比单个线圈自感稍小一点，而不会是其值的1／2、1／3或1／4。

表2 接入不同数量线圈时的有效电感系数

3 试验测试

采用常州安柏精密仪器有限公司的AT2816A型精密LCR数字电桥对螺线圈回路的电感系数进行测试。该设备采用万能电桥法，通过给螺线圈回路接入测试信号电平，从而自动测量回路的电感、电容、电阻和品质因数等参数。图4为试验室搭建的磁场发生线圈实物照片，表3给出了仿真值和测试值的比较。

测试了单个线圈和多个线圈并联的情形，串联方式由于用于连接的长导线数量有限（每根均需10 m左右），仅测试了线圈1和线圈2串联。从表3可以看出：ANSYS仿真值和测试值基本能够吻合，误差在16.5%以内（理论公式无法计算多线圈并联或串联的情形）。导致理论公式计算值、ANSYS仿真值和测试值不一致的原因主要在于计算模型和实体模型间的差异。对于实际绕制螺线圈的半径5 mm，壁厚1 mm的空心导体，在ANSYS仿真计算时视为不计线径的细导线，而在采用理论公式计算时视为半径5 mm的实心导体。另外，实际绕制的线圈并非理想的圆形，线圈匝间距控制不严，并非完全相等，这些因素均会影响实际线圈组的电感值，因此，ANSYS仿真值和测试值出现一定的偏差是合理的。

图4 磁场发生线圈实物照片

表3 3种方法计算的螺线圈电感系数

4 结论

为解决低频强磁场模拟试验系统中的磁场发生线圈电感系数难以确定的难题，首先采用理论公式计算了单个疏绕螺线圈的自感，再利用ANSYS有限元仿真对三组两个疏绕螺线圈的有效电感系数进行了计算，从而推算出了利用公式难以直接计算的线圈间互感，最终给出了线圈组中4个疏绕线圈串并灵活接法时的电感系数值，为通过调整线圈连接形式和数量来调节脉冲磁场上升时间及频谱提供了可能。计算结果为低频强磁场模拟试验室磁场发生线圈的设计及其RLC脉冲电流激励电路参数的确定提供了直接依据。

［1］ Guru B S，Hiziroglu H R.Electromagnetic Field Theory Fundamentals［M］.2 ed.England：Cambridge University Press，2004.

［2］葛宇宏，葛志利.有限长多层直螺线管的自感系数［J］.大学物理，2010，29（7）：16－19.

［3］张永吉.稀疏螺线管自感的计算［J］.江南大学学报，1989，5（2）：135－137.

［4］王庆峰，刘庆想，张政权.低阻抗脉冲形成网络引线电感的模拟及实验研究［J］.强激光与粒子束，2011，23（6）：1697－1700.

［5］王磊磊，刘文，吴榴红.等.电磁轨道炮二阶过阻尼电路的模型构建及分析［J］.河南科技大学学报：自然科学版，2012，33（6）：69－73.

［6］ Л.Д.朗道.连续媒质电动力学（上册）［M］.北京：人民教育出版社，1963.

［7］ Symons W R.静电学和电动力学（下册）［M］.北京：科学出版社，1985.

［8］王长清.现代计算电磁学基础［M］.北京：北京大学出版社，2005.

［9］宫野.计算多重积分的蒙特卡罗方法与数论网格法［J］.大连理工大学学报，2001，41（1）：20－23.

［10］徐士良.计算机常用算法［M］.2版.北京：清华大学出版社，1995.

O441.4

1672－6871（2014）06－0052－05