并网运行风电机组电压稳定性分析
2014-06-07韩肖清王康宁
肖 春,韩肖清,王康宁
(1.太原理工大学电气与动力工程学院,山西 太原 030024;2.山西省电力科学研究院,山西 太原 030024)
并网运行风电机组电压稳定性分析
肖 春1,韩肖清1,王康宁2
(1.太原理工大学电气与动力工程学院,山西 太原 030024;2.山西省电力科学研究院,山西 太原 030024)
分析了并网运行的风电机组对电力系统电压稳定性的影响。从静态电压稳定性角度,将风电机组等效成随风速变化的有功和无功电源,分析了风电机组的控制方式、无功功率出力对电压稳定性的影响。动态稳定性的研究中,采用IEEE39节点标准测试系统,仿真结果表明:在提高电压稳定性方面,恒电压控制比恒功率控制具有明显的优越性。
电压稳定;并网运行;风电机组;极限传输功率
0 引言
风能作为一种清洁、可再生的能源,得到迅速发展。随着大规模风电机组并网接入电力系统,会给电网的电能质量、稳定运行带来影响,研究风电机组接入电力系统的稳定性问题[1-3]迫在眉睫。电压稳定性[3]是电力系统在正常情况下或遭受扰动之后所有节点维持可接受电压的能力。当系统受到扰动而进入电压不稳定状态时,负荷需求的增加或系统状态的变化将引起电压不可控的连续下降。引起电压失稳的主要因素是电力系统无功功率的严重不足。因此,研究并网运行的风电机组的系统电压稳定性和动态稳定性很有实用价值[4-6]。文献[2]总结了国内外对风电系统电压稳定性的研究现状,提出需要深入研究电压稳定性。文献[7]在PSCAD/EMTDC平台上建立仿真模型,研究了双馈风力发电机组并网后系统的稳定性。文献[8]基于双馈风机的T型等值模型[9],通过PSASP软件仿真,表明对双馈风电机组采用恒电压控制的优势。但是都没有涉及对线路极限传输功率的研究,对功角稳定性的研究也比较有限。
本文将风电机组等效成随风速变化的有功和无功电源,研究风电机组的电力系统静态电压稳定性和动态稳定性,分析了风电机组的控制方式、无功出力对线路极限传输功率的影响。采用美国邦纳维尔电力局公司和中国电力科学研究院共同开发的BPA程序,对风电机组和常规同步发电机运行特性进行分析对比。
1 电压稳定性
电压稳定性可以通过P-V曲线进行描述,如图1所示,即系统的传输功率与负荷节点电压之间的关系。图1中,P表示某负荷节点功率,V表示母线的电压。P-V曲线的上半支是系统稳定运行点,下半支是不稳定运行点,而P-V曲线的上半支向下半支过渡时的拐点,为电压稳定的临界点。
为保证电力系统可靠、稳定地运行,对电压会有一定的限制,本文以电压不超出±0.05为要求,提出了电压的稳定裕度,如图2所示,图2中,Pmax、Vmax为最大功率点,定义V=0.95时的功率为系统的允许功率Pallow。因此,为保证系统运行有一定的稳定裕度,传输功率只能小于等于Pallow。
2 风电机组的稳定性分析
2.1 静态稳定性分析
根据风电机组的工作原理,将风电机组等效地用随风速变化的有功和无功电源表示,如图3所示,

图1 负荷节点的注入有功功率与电压之间的关系

图2 稳定裕度
图3中,PWT为风电机组注入电网的有功功率;QWT为风电机组注入电网的无功功率,分别见式(1)和式(2);UWT为风电场出口电压;GWT为可变电导;BWT为可变电纳。

当变频器电流到达极限时,风力发电机可以看成是电流一定的恒电流源,其导纳有如下关系:


图3 风电机组等效电路
此时,电流达到变频器最大电流,风电机注入电网的电流为:

2.2 动态稳定性分析
风电机组控制方式有恒功率因数控制和恒电压控制两种。当按恒功率控制时,即风电机组的电导和电纳随端电压变化而变化;当按恒电压控制时,风电机组的电导和电纳随功率因数的变化而变化。
对于风电机组的动态仿真,需要研究风电机组的特性。例如,变速恒频风电机组通过变频器与电网相连,电力电子元件对过电流非常敏感,当电网故障时,变频器的控制器会立即发现,为了保护变频器,变速风机会与电网分裂,从而引起大范围的电压降落,甚至会影响到整个系统。为此,根据《国家电网公司风电场接入电网技术规定》,风电场低电压穿越要求为:“风电场内的风电机组具有在并网点电压跌落至20%额定电压时能够保持并网运行625 ms的低电压穿越能力”。
为了准确描述风电机组的动态性能,本文采用BPA计算程序,给出了风电机组的动态模型,如图4所示,主要包括发电机、变频器模块,电气控制模块和涡轮机及其控制模块。

图4 风电机组动态模型
3 算例分析
3.1 静态分析仿真系统
将如图5所示电压稳定性测试系统[10]中节点3的同步发电机组用同容量的风电机组代替后的系统,作为风电机组稳态分析的算例系统。简化后的等值电路如图6所示。

图5 仿真算例系统
图6中,从负荷两端向左看去,进行戴维南等效,则等值电势和等值阻抗分别为:
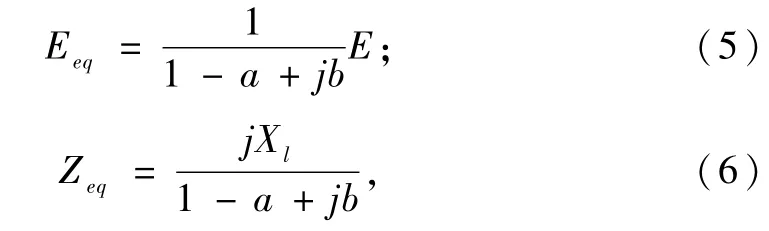
式中,a=Xl(Bl+BWT);b=XlGWT。因此,当负荷功率因数cosφ一定时,提供给负荷的最大功率为:

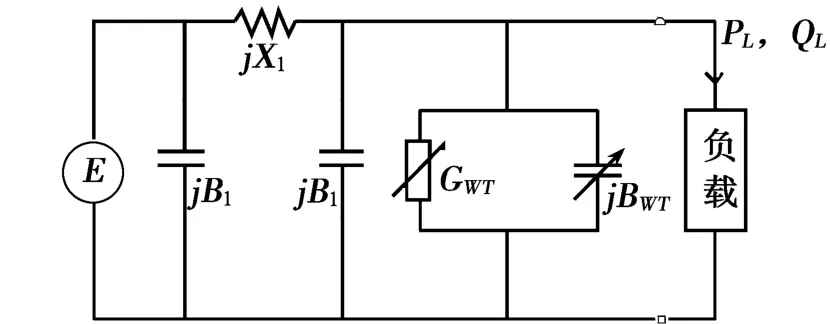
图6 等值系统
相对应的负荷电压为:

当风电机组发出无功功率增加时,意味着 a增加,因此,提供给负荷的最大传输功率极限增加;同时,相应的负荷最大电压也增加。
3.2 静态分析仿真
节点3的风电机组分别采用恒电压控制和恒功率因数两种控制方式,记为Case1和Case2。低风速条件下,所有负荷功率因数为0.9滞后,节点7和节点10的负荷均由50%恒功率负荷、25%恒电流负荷和25%恒阻抗负荷组成。
3.2.1 风电机组的控制方式对最大极限传输功率的影响
图7为节点10负荷增加时的P-V曲线。由图7可见:运行电压0.95时,风电机组采用恒电压控制要比恒功率因数控制的负荷极限传输功率增加450 MW,提高了13.2%。
3.2.2 风电机组无功功率出力对极限传输功率的影响
恒功率因数控制下的风电机组,节点10的Pmax和相应的Pallow随无功功率变化情况如图8所示。图8中,随着风电机组注入系统无功的增加,Pmax从3 600 MW增加到3 800 MW;Pallow从3 300 MW增加到3 500 MW。

图7 节点10的P-V曲线
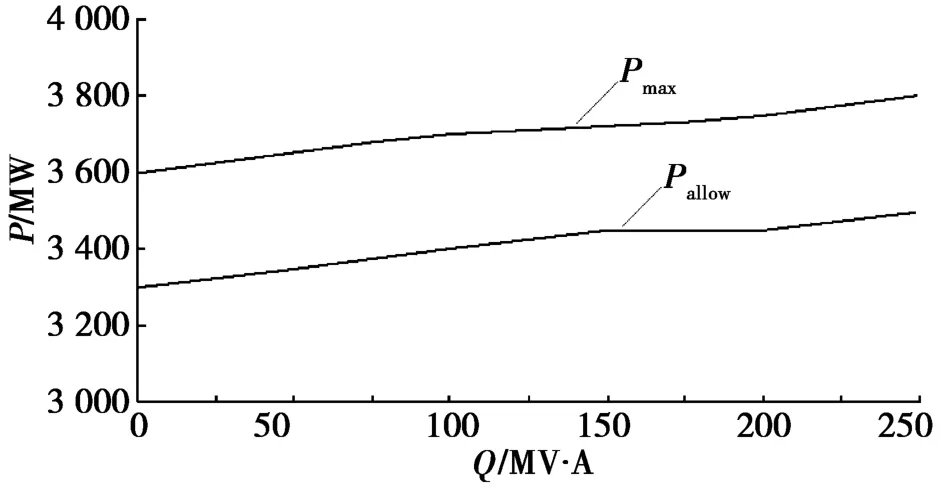
图8 风机无功出力与节点10的功率极限关系
3.2.3 有载调压变压器分接头调节对稳定性的影响
为了分析有载调压变压器自动调整分接头对稳定性的影响,现假设节点6和节点8之间的变压器为有载调压变压器。若t=1 s节点5和节点6之间的一回线路发生三相短路被切除,故障暂态过程中系统电压急剧下降;t=6.8 s时,有载调压变压器动作,自动调整节分接头,观察节点6、节点8电压和风力发电机组无功出力随时间的变化情况,如图9所示。
情况1:分接头调节可以使变压器低压侧节点8电压升高0.4。但是节点6电压却由于分接头调节还略有减小,下降了0.02。此时,风电机组的无功功率出力由于其端电压下降而增大,从而使节点电压维持在扰动之前的水平。
情况2:有载调压变压器动作试图使节点8电压升高,但是效果不明显,却使节点6电压随之下降。由于恒功率因数控制风电机组没有无功出力的支持,系统无功功率水平下降,使得最终的稳态电压均有下降。
3.3 动态分析系统
本文采用IEEE39节点标准测试系统[11]作为研究风电机组的动态特性的算例系统,系统参数见文献[12-13]。仿真中针对同一节点,分别以常规同步发电机、恒功率因数控制的风电机组和恒电压控制的风电机组为电源进行分析对比,记为情况1、情况2和情况3。风电机组和同步发电机组按同容量仿真。
3.4 动态分析仿真
3.4.1 系统扰动的响应
发电机出口侧线路始端发生三相短路,持续0.04 s后切除故障线路。风电机组运行在高风速下。3种情况的发电机出口电压、无功功率和有功功率随时间的变化情况,如图10所示。
从图10中可以看出:暂态过程中同步发电机组的电磁功率的振幅较大,最大变化幅度425.85 MW,而风电机组的幅度比较小,恒功率因数控制的风电机组电磁功率变化幅度为78.17 MW,恒电压控制的风电机组为39.085 MW。

图9 风电机组电压和无功功率曲线
风电机组运行在高风速下,其无功调节能力比同步发电机差,在暂态过程中无功出力基本不变,稳态电压也低,同步发电机电压为0.96,恒电压控制风电机组为0.91,恒功率因数控制为0.89。
3.4.2 系统频率变化的响应
发电机的机组容量为830 MW,情况2、情况3系统的风电穿透功率为13.4%。切除容量为180 MW的同步发电机后,系统的频率随时间变化的情况如图11所示。
情况1、情况2和情况3的频率偏差分别为0.54 Hz、1.40 Hz和1.65 Hz。
同步发电机与风电机组相比,有很好的频率支持能力。但从图11也可以明确看到:在暂态过程中,风电机组可以提供给系统短暂的频率支持,这部分能量储存在风电机组转子中,在暂态过程中释放出来。
采用恒电压控制方式,可以通过支持系统无功,提高运行电压,减少有功损耗,从而减少系统有功功率缺额,间接地支持系统频率。从图11中可以看出:恒电压方式的最终频率偏差比恒功率因数方式要小。
4 结论
(1)通过对静态电压稳定性分析,得到如下结论:增加风电机组的无功出力,可以提高线路输送功率的水平;变速恒频风电机组的恒电压控制与恒功率因数控制相比,可以提高输电线路传输功率极限。有载调压变压器分接头调节可以提高负荷侧节点电压,但是却有可能由于系统无功功率不足,使得系统其他节点电压下降,最终有可能引发电压崩溃。为了提高系统的无功功率水平,风电机组采用恒电压比恒功率因数控制效果好。
(2)通过对动态电压稳定性分析,得到如下结论:风电机组可以提高系统的极限切除时间;恒电压控制与恒功率控制相比,有利于暂态后电压的快速恢复。

图10 同步机和风机两种控制方式对比曲线

图11 同步发电机和风电机组的频率曲线
[1] 张瑞明,张新燕.含风电场的系统电压稳定性分析[J].华东电力,2009,37(9):1575-1578.
[2] 马幼捷,杨海珊,周雪松,等.风电系统的电压稳定性分析[J].电力系统及其自动化学报,2010,22(3):22-26.
[3] 隋新,刘扬,韩红彪,等.网络式风电监控数据采集系统[J].河南科技大学学报:自然科学版,2013,34(4):31-35.
[4] 夏道止.电力系统分析[M].北京:水力电力出版社,1995.
[5] 林莉,陈亚宁,周溶,等.并网型风电场电压稳定研究[J].华东电力,2008,36(3):58-61.
[6]El-Shimy M,Badr M A L,Rassem O M.Impact of Large Scale W ind Power on Power System Stability[C]//12th International Middle East Power System Conference.Aswan,Egypt:South Valley University,2008:630-636.
[7] Prabha K.电力系统稳定与控制[M].北京:中国电力出版社,2002.
[8] 赵清声,王志新.双馈风力发电机组系统接入与稳定运行仿真[J].电网技术,2007,31(22):69-74.
[9] 丁明,李宾宾,韩平平.双馈风电机组运行方式对系统电压稳定性的影响[J].电网技术,2010,34(10):26-31.
[10] Lei Y Z,Alan M,Lightbody G,et al.Modeling of the W ind Turbine with a Doubly Fed Induction Generator for Grid Integration Studies[J].IEEE Trans on Energy Conversion,2006,21(1):257-264.
[11] Taylor CW.电力系统电压稳定[M].北京:中国电力出版社,2002.
[12] 王安斯,罗毅,涂光瑜,等.基于事故链风险指标的输电脆弱度在线评估方法[J].中国电机工程学报,2010,30(25):44-50.
[13] 韩肖清.含变速恒频风电机组的电力系统仿真与稳定性分析[D].太原:太原理工大学电气与动力工程学院,2009.
TM76
A
1672-6871(2014)06-0047-05
国际科技交流与合作专项基金项目(2010DFB63200);山西省高等学校中青年拔尖创新人才支持计划基金项目
肖 春(1987-),女,山西永济人,硕士生;韩肖清(1964-),女,山西太原人,教授,博士,博士生导师,研究方向为电力系统运行与控制、新能源技术.
2014-03-22
