基于相邻信号点的自适应变模盲均衡算法

张艳萍，郭 薇，张 健

（南京信息工程大学电子与信息工程学院，江苏 南京 210044）

基于相邻信号点的自适应变模盲均衡算法

张艳萍，郭 薇，张 健

（南京信息工程大学电子与信息工程学院，江苏 南京 210044）

针对基于星座图划分的正交幅度调制盲均衡算法迭代初期误判率较高的缺点，在分析正交幅度调制信号自适应变模盲均衡算法的基础上，提出了一种改进的自适应变模算法。该算法在对每个星座点都均衡的同时，还将相邻星座点的影响考虑在内，并采用新的加权因子选取方法动态控制相邻星座点的权重比例，使得算法的误判率降低，从而具有更快的收敛速度。不同的水声信道仿真实验进一步验证了该算法在收敛速度上的优越性。

盲均衡；同相正交；自适应变模；误差函数

0 引言

水声信道的带宽非常有限，且存在着严重的多途干扰，在很大程度上限制了水下通信的速率和可靠性。盲均衡算法不必发送训练序列，节省了大量水下信道带宽，有效地提高了信息的传输速率，非常适合于水声信道的均衡［1］。正交幅度调制（QAM）是现代通信的重要手段，如何提高此类信号的盲均衡性能是本领域研究的热点［2］。在盲均衡技术中，对于模值不为常数的QAM信号，常数模算法（CMA）虽可对其稳健收敛，但是收敛后的均方误差很大且无法纠正相位旋转，这会造成较高的误码率。文献［3］提出了一种多模算法（MMA），可较好地消除信号的相位模糊，得到了较广的应用，但MMA算法的码间干扰仍较大。为了进一步降低算法的码间干扰，文献［4］提出了一种自适应变模算法（AVMA），该算法首先对星座图进行划分，并根据均衡器的输出采用对应区域内星座点的模值来均衡，达到了对星座图中每个信号点都进行均衡的目的，从而在纠正相位旋转的同时，有效地降低了算法的码间干扰，但该算法会增大对QAM信号均衡时产生的误判，使均衡器抽头系数误调整的可能性增大，导致算法收敛速度减慢。

本文在文献［4］的基础上对AVMA算法进行改进，在保证对每个信号点都进行均衡的基础上将相邻信号点的信息考虑在内，提出了基于相邻信号点的改进AVMA算法（MAVMA），该算法能够减少AVMA算法对QAM信号均衡时产生的误判，使得均衡器抽头系数误调整的可能性变小，从而加快了收敛速度。

1 自适应变模算法

针对16QAM信号的星座图特点，文献［4］将均衡器输出值的同相分量和正交分量分别采用不同的均衡区域，划分区域如图1所示。图1将16QAM信号从正交和同相两个方向分别按照星座点的模值分为两个区域（区域1和区域2），每个区域内的模值相同，均衡区域以相邻星座点距离的一半划分。均衡器输出y（k）的实部yR（k）和虚部yI（k）分别对应同相和正交均衡图内的均衡区域，所以y（k）和星座点是一一对应的，从而达到了对每个星座点都进行均衡的目的。

AVMA算法的代价函数为：

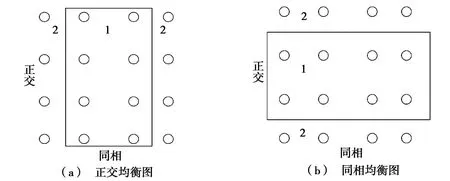
图1 16QAM信号星座图同相和正交均衡区域

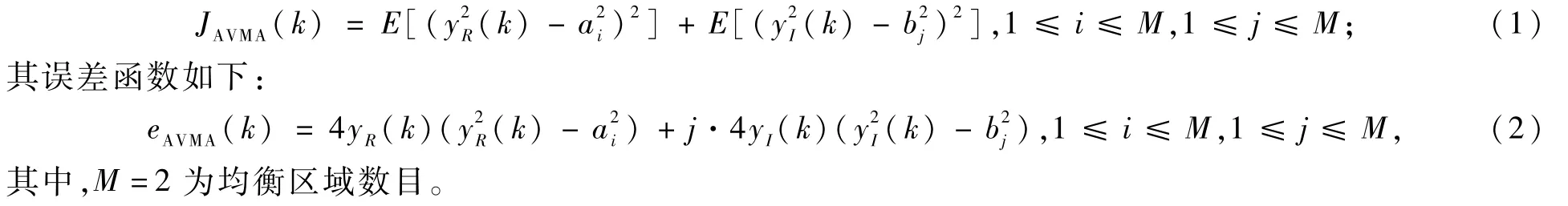
从式（1）的代价函数可以看出：ai和bj中的下标i和j的取值确定了星座点所在的位置，因此，AVMA算法中同相分量ai和正交分量bj可以表示QAM信号中所有星座点。AVMA算法做到了对区域内的每个信号点都单独进行均衡，包含了星座图的全部信号点信息，误差模型更匹配16QAM信号的星座图，有效地降低了码间干扰。但由于均衡的星座点数的增加使得收敛速度减慢，同时降低了算法的稳定性。

2 引入相邻信号点的自适应变模算法

在AVMA算法的迭代初期，抽头系数远没有达到最优，并且由于噪声的存在，均衡器输出会落在一个错误的区域。这种错误的判决反馈使得算法经过很多次迭代后才能收敛，从而降低了收敛速度。在基于梯度下降的自适应盲均衡代价函数中，如果能包含部分或全部信号星座图信息，则可以有效地改善接收机的性能［5－6］。

依据以上分析，为了提高AVMA算法的收敛速度，本文引入相邻信号点的信息，提出了改进算法MAVMA。以16QAM信号为例，星座图的区域划分如图2所示。

图2 16QAM星座图划分区域

在图2的16QAM星座图划分区域中，Al表示第l个均衡区域。首先从正交方向考虑，假设均衡器输出的实部落在区域 Al，R中，由于存在误判，其误差函数不仅要考虑主区域Al，R，还要考虑其相邻区域Al－1，R和Al＋1，R。如果Al，R是星座图边缘的区域，其相邻区域则只有1个。在图2a中，假设均衡器输出的实部落在区域A3，R中，则A3，R为主区域，A2，R和A4，R为相邻区域。从同相方向考虑也是如此，划分区域如图2b所示，A3，I为主区域，A2，I和A4，I为相邻区域。由于除相邻星座点以外的其他星座点对主区域的影响较小，若将这些星座点都考虑到算法中不仅对减少误判没有太大帮助，反而会增加算法复杂度，所以本文只考虑与主区域相邻的星座点对算法的影响。

MAVMA算法由于引入了相邻星座点的信息，使得均衡器抽头系数在迭代初期误调整的可能性减小，加快了收敛速度，增强了算法的稳定性。然而，也正因为相邻星座点的引入使得算法的误差eMAVMA增大，因此，需要选择合适的权重因子βi来控制两个误差函数的比重，使算法在达到稳定收敛时相邻星座点的误差快速减少并逐渐趋向于零［7］。本文中的加权因子βi不采用常数形式，而采用文献［8］的思想动态控制，并根据同相和正交方向的均衡将βi分为实部和虚部两部分，从而更为准确地控制βi的取值。

其中，el，DDR（k）和el，DDI（k）分别为主区域l中DD算法误差函数el，DD（k）的实部和虚部。α值控制权重因子 βi的变化速度，以实部为例，得到α取不同参数时 βi，R与el，DDR（k）的关系曲线，如图3所示。

由图3可以看出：α＝10时曲线变化较为平缓，即随着el，DDR（k）的减小βi，R降低的速度较慢，最终会影响MAVMA算法收敛速度的提高。随着α的增大，曲线变得越来越陡峭，此时，βi，R可以在某个时刻从0.25快速减小并无限趋于0，符合本文提出的MAWMA算法对权重因子βi的要求；但过大的α取值使得βi，R开始减少的时刻后延，不利于算法码间干扰的降低。经过多次试验验证后令α＝30，该方法同样适用于βi，I的取值。

式中，ai，R和ai，I分别为对应区域内信号点的同相分量和正交分量。

图3 α取不同参数时βi，R与el，DDR（k）的关系曲线

3 仿真结果与性能分析

为了验证MAVMA的有效性，利用Matlab进行信道仿真实验。以16QAM信号为例，采用T／2分数间隔均衡器，中心双抽头初始化，信噪比为25 dB，分别采用两个不同信道进行均衡，信道噪声为高斯白噪声，MMA、AVMA及MAVMA算法的迭代步长均为0.006，50次独立蒙特卡罗仿真实验。在算法性能评价上，采用输出端的剩余码间干扰（ISI）进行评价［9］：

实验1 采用文献［10］中的浅海信道h1均衡，均衡器长度为16，其他仿真条件不变，h1＝［0.584 87 －1 0.260 84 －0.133 64 0.074 006 －0.039 385 0.018 292 －0.005 903 7］，仿真结果见图4和图5。

从图4的性能曲线中可以看出：MMA算法在迭代约1 500次时，码间干扰达到－22 dB，虽收敛速度快但码间干扰大。由于对每个星座点都进行均衡，AVMA算法和本文所提出的MAVMA算法收敛后剩余码间干扰均较小，约为－34 dB，较之MMA约降低了12 dB。同时可以看出：在收敛速度上，AVMA在迭代约9 500次时达到收敛，而MAVMA算法在迭代约2 500次时就进入稳态收敛阶段，收敛速度优于AVMA约7 000次。

这是由于MAVMA在对每个星座点进行均衡的同时将相邻星座点信息也考虑在内，减少了误判的机率，提高了收敛速度。

从图5a的星座图中可以看出：信号均衡前星座图模糊且无法辨识，图5b为MMA算法的星座图输出，星座点清晰可见。图5c和图5d分别为AVMA和MAVMA算法的星座图输出，AVMA和MAVMA算法均衡后的星座图比MMA更加清晰可见，相邻星座点分得更开。同时从图4可知：所提出的MAVMA算法和AVMA收敛后的星座图基本没有差别，即两种算法收敛后码间干扰相同。

实验2 采用文献［11］中的负声速梯度信道并添加π／3的相位旋转得到信道h2＝［0.965 6 0.090 6 0.057 8 0.236 8］×exp（－j×π／3），均衡器长度为8，其他仿真条件保持不变，仿真结果如图6所示。

图4 浅海信道均衡的码间干扰曲线比较

图5 浅海信道均衡的星座图比较

从图6中可以看出：MMA在迭代1 000次时码间干扰达到－26 dB，而AVMA和MAVMA算法分别在迭代2 000次和2 500次时码间干扰就达到－39 dB，较之MMA约降低了13 dB。在收敛速度上，MAVMA在保持较低码间干扰的同时收敛速度比AVMA提高约500次。

比较图4和图6的性能曲线可知：由于浅海信道h1受海面、海水介质、鱼虾船只等因素的影响，其传播条件较为恶劣，所以盲均衡算法初期误判率较高，达到稳态时码间干扰与h2信道均衡时相比较大，而采用MAVMA算法均衡减少了误判，收敛速度明显优于AVMA。负声速梯度信道h2的零极点全部位于单位圆内部，是一条最小相位信道，均衡难度较小，误判率较低，达到稳态时码间干扰小，所以MAVMA均衡后收敛速度只提高约500次。同时也说明，水声信道特性直接影响水声通信的性能。

图6 负声速梯信道均衡的码间干扰曲线比较

4 结束语

针对AVMA算法误判率较大的缺点，提出了一种基于相邻信号点的改进算法MAVMA。通过引入相邻星座的信息来减少误判从而提高了收敛速度，并采用DD算法误差函数的变化规律动态控制β因子的取值，对误差函数的权重比例进行了更为准确的控制。通过不同的水声信道仿真实验对比，其收敛速度和码间干扰分别优于文中提到的AVMA和MMA算法，具有一定的实用价值。

［1］ 张艳萍.水声通信信道盲均衡理论与算法［M］.北京：气象出版社，2009.

［2］ 薛伟，杨小牛，张朝阳.一种改进的加权多模盲均衡算法［J］.系统仿真学报，2011，23（3）：451－455.

［3］ Yang J，Werner J J，Dumont G A.The Multi-modulus Blind Equalization and Its Generalized Algorithm［J］.IEEE Journal on Selected Areas in Communications，2002，20（5）：997－1015.

［4］ Shahzad A S，Pingzhi F.Joint Blind Equalization＆Carrier Phase Recovery Based on Adaptively Varying Modulus Algorithm（AVMA）［C］／／IEEE INMIC 2005，9 th International Multitopic Conference.2005.

［5］ He L，Amine M，Reed C.A New Adaptive Equalizer for QAM Signals［C］／／Proc IEEE，Sarnoff Symp.NJ，2001.

［6］ 王彬，葛临东，霍亚娟.适用于高阶QAM信号的多模混合盲均衡算法［J］.数据采集与处理，2011，26（1）：8－14.

［7］ 张艳萍，崔伟轩.引入动态动量因子的共轭梯度多模盲均衡算法［J］.河南科技大学学报：自然科学版，2013，34（3）：40－44.

［8］ Rangeet M，Tarun C.A Variable Step Size Square Contour Algorithm Based on a Novel Non-linear Function of Error Signal［C］／／IEEE.2011：336－338.

［9］Kashif N P，Azzedine Z.A Newton-like Algorithm for Adaptive Multi-modulus Blind Equalization［C］／／2011 7th International Workshop on Systems，Signal Processing and Their Applications（WOSSPA）.2011：283－286.

［10］ Adam Z，Young H，Wu L X.Performance Analysis of Digital Acoustic Communication in a Shallow Water Channel［J］. IEEE Journal of Oceanic Engineering，1995，20（4）：293－298.

［11］ 艾宇慧.水声数字通信［D］.哈尔滨：哈尔滨工程大学，1999.

TN911.5

A

1672－6871（2014）06－0034－05

国家自然科学基金项目（61203273）；江苏省高校自然科学研究重大项目（13KJA510001）；江苏省“六大人才高峰”培养对象基金项目（2008026）；江苏省高校科研成果产业化推进工程基金项目（JHB2012－9）；江苏省高校“传感网与现代气象装备”优势学科建设项目

张艳萍（1966－），女，山西临汾人，教授，博士，硕士生导师，研究方向为通信信号处理和水声通信.

2014－02－04