双列圆锥滚子轴承动力学分析

胡广存，魏铁建，邓四二，贾永川，张 雪

（1.河南科技大学机电工程学院，河南 洛阳 471003；2.许昌职业技术学院机电工程汽车系，河南 许昌 461000；3.南京林业大学机械电子工程学院，江苏 南京 210037）

双列圆锥滚子轴承动力学分析

胡广存1，魏铁建2，邓四二1，贾永川1，张 雪3

（1.河南科技大学机电工程学院，河南 洛阳 471003；2.许昌职业技术学院机电工程汽车系，河南 许昌 461000；3.南京林业大学机械电子工程学院，江苏 南京 210037）

基于滚动轴承动力学理论，建立了双列圆锥滚子轴承动力学分析模型。采用精细积分法和预估 －校正Adams-Bashforth-Moulton多步法相结合的方法，对轴承非线性动力学微分方程进行求解。研究了双列圆锥滚子轴承的最大接触压力、滚子打滑率、滚子歪斜角以及轴承疲劳寿命等动态性能。分析结果表明：轴承的最大接触压力随轴向预紧量的增加呈先减小后增大的趋势，最佳预紧量随外载荷的增加而变大；滚子歪斜角随径向载荷的增加而变大，“压紧”侧的滚子歪斜角略微大于“放松”侧；轴承疲劳寿命随轴向预紧量的增加而增大直至最大值，随后迅速下降。

轴承动力学；双列圆锥滚子轴承；轴向预紧量；疲劳寿命

0 引言

双列圆锥滚子轴承具有承载能力大，可同时承受径向和轴向联合载荷以及寿命长等性能，被广泛应用于汽车、机床、机车、轧机等重型机械行业。作为重要的动力传动部件，双列圆锥滚子轴承的动态性能直接影响到整机的正常运行。

文献［1］首先提出了动力学分析模型，研究了4个自由度滚动体和6个自由度保持架的位移、速度以及轴承内部的打滑等，但是没有考虑轴承受力不平衡时所产生的惯性力和惯性力矩的影响。随后，文献［2］根据动力学微分方程建立了滚动轴承动力学分析模型，对包括圆锥滚子轴承在内的各类轴承进行了全面的动态分析，但该分析模型十分复杂，未能在实际中得到应用。文献［3］利用数值计算方法对双列圆锥滚子轴承动力学微分方程进行求解，提出了双列圆锥滚子轴承的综合模型，研究了轴承在非New ton流变模型下的拖动等性能，但忽略了保持架的平移运动。国内学者也对轴承力学性能进行了研究。文献［4］对弹性接触问题的基本方程进行了研究，给出了圆锥滚子轴承接触应力的简化算法和步骤。文献［5］研究了圆锥滚子轴承负荷分布并给出了相应的计算方法，建立了轴承系统承载运行时的平衡方程。

目前，国内外对圆锥滚子轴承的研究大多以单列为主，对双列圆锥滚子轴承的动力学分析较少。鉴于此，针对某一型号双列圆锥滚子轴承，利用滚动轴承动力学理论［6］，结合圆柱滚子轴承仿真分析［7］，建立双列圆锥滚子轴承动力学分析模型，采用精细积分法和预估－校正Adams-Bashforth-Moulton多步相结合的方法，对轴承非线性动力学微分方程进行求解，并开发了双列圆锥滚子轴承动力学分析软件DTRB／HKD。在此基础上，研究了双列圆锥滚子轴承滚子与滚道、大挡边间的最大接触压力，滚子打滑率、滚子歪斜角以及轴承疲劳寿命等动态性能，为今后轴承的优化分析提供了理论性指导。

1 轴承动力学模型

图1为双列圆锥滚子轴承几何模型示意图。双列圆锥滚子轴承的两个内圈通过锁扣连结在一起，并进行固定，外圈以角速度ωe带动保持架与滚动体一起旋转。为了便于分析，引入以下主要坐标系：原点在轴承中间横截面上的空间惯性坐标系（X，Y，Z），外圈坐标系（Xe，Ye，Ze）以及滚子坐标系（Xrm，Yrm，Zrm）。下标m表示轴承列数，m＝1，2（表示轴承列1和列2，下同）。

1.1 滚动体与滚道间的接触载荷

双列圆锥滚子轴承会受到轴向载荷、径向载荷以及倾覆力矩的综合作用，滚动体发生倾斜、歪斜，使轴承内部相互作用变得更为复杂。针对上述问题，本文采用“切片法”［8］计算滚子与滚道间的接触载荷，如图2所示。根据经典Hertz弹性线接触理论，每一切片上滚动体与滚道间的接触压力为：

式中，qi（e）jk是第j个滚子第k个切片与内外滚道的法向接触压力；Ki（e）是滚子与内外滚道接触处的负荷－变形常数；δi（e）jk是第j个滚子第k个切片与滚道间的弹性变形量；i、e分别表示内、外滚道（下同）。

滚子与滚道间的总接触载荷，可由滚动体有效接触长度Ls上每一片与滚道的接触压力沿滚动体轴线方向进行积分求和得到：

图2 滚子与滚道间作用力

1.2 滚动体与滚道间的拖动力

滚动体与滚道间的润滑剂在挤压过程中会在接触表面形成润滑油膜。滚动体与内外滚道接触处由于相对滑动引起的摩擦力可根据润滑剂的拖动力来计算。图2为滚子与滚道间作用力，沿着滚动体轴线方向对滚动体进行切片，则滚子与滚道间的拖动力为每一片上拖动力的总和：

每一切片上的拖动力可表示为：

式中，qi（e）jk是第j个滚子第k个切片与内外滚道的法向接触压力；μi（e）jk是第j个滚子第k个切片的润滑油膜拖动系数，见参考文献［9］。

1.3 滚动体与内圈大挡边间的接触载荷

轴承在运转过程中，滚动体通常与内圈大挡边接触。此处假设圆锥滚子大端面为球形基面，内圈大挡边为锥形面。滚子与大挡边间接触处表面上会产生一接触椭圆区，如图3所示。在接触椭圆区域上，假设滚动体与大挡边间的作用力作用在最大弹性变形点处，则根据文献［10］的研究成果可得到滚子端部与大挡边间接触力为：

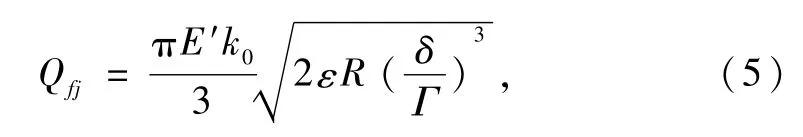
图3 滚动体与大挡边间作用力

式中，k0＝1．033 9（Rη／Rξ）0．636；Rη、Rξ为两物体接触点处的等效曲率半径；E′为滚动体与轴承内圈大挡边的当量弹性模量

滚子大端端面与大挡边间的摩擦力为：

滚子大端端面与大挡边间的摩擦力矩为：

式中，μfj为滚子大端球基面与挡边间接触点的摩擦因数［11］；h为滚子大端球基面与挡边接触点的高度；L1为滚子偏斜中心距滚子大端的距离；αzj、αyj分别为滚子的倾斜角及歪斜角。

1.4 滚动体与保持架间的接触载荷

滚动体在滚道上滚动，同时又在保持架兜孔内绕自身轴线进行转动。当滚子公转速度大于保持架公转速度时，滚子推动保持架向前运动；滚子公转速度小于保持架公转速度时，滚子阻碍保持架向前运动。滚动体与保持架兜孔之间既存在法向接触载荷，也存在着切向摩擦力，如图4所示。滚动体与保持架兜孔间的法向接触载荷计算，可采用滚动体与滚道间接触载荷的“切片法”，滚子与保持架兜孔间的接触载荷计算如下：

图4 滚动体与保持架兜孔间作用力

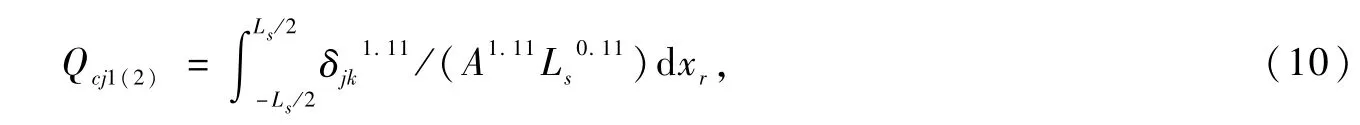
式中，Qcj1（2）为滚子与保持架兜孔间的法向接触载荷；A为弹性变形量与外部载荷之间的系数，A＝1.36η0．9，η为两接触物体的综合弹性常数；Ls为滚子有效接触长度。

滚子与保持架兜孔间的摩擦力和力矩分别为：

式中，μcj为滚子与保持架兜孔间的摩擦因数［10］为润滑剂动力黏度，nrol为滚子自转角速度；Qcj1（2）为滚子与保持架兜孔间的法向接触载荷。

1.5 轴承动力学微分方程

根据轴承内部间的相互作用，得出轴承各个部件在平动和转动方向上的动力学微分方程，本文以轴承动圈（外圈）为例，列出双列圆锥滚子轴承的外圈动力学微分方程：

轴承外圈质心在平动方向上的动力学微分方程，

轴承外圈围绕自身轴线旋转的动力学微分方程，

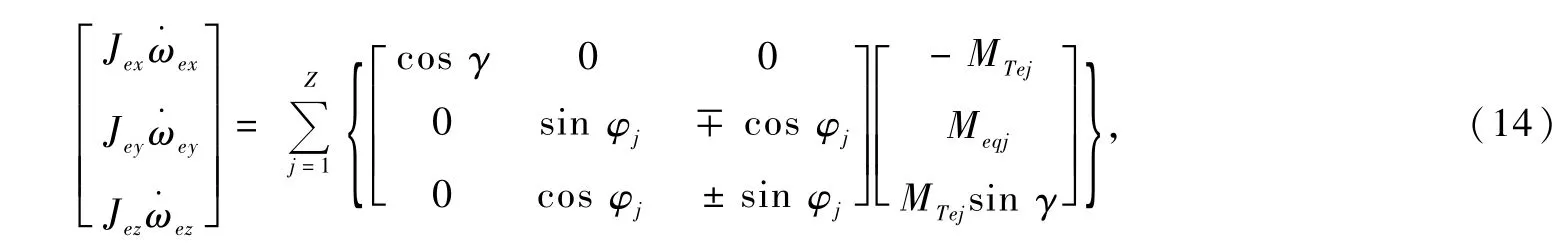
式中，列1取上面的符号，列2取下面的符号；Ge为外圈质量为外圈质心沿着惯性坐标系（X，Y， Z）的位移加速度分别为外圈绕惯性坐标系（X，Y，Z）的转动惯量；φj为双列圆锥滚子轴承第j个滚动体在惯性坐标系下的方位角；αi、αe为内外滚道接触角，γ为平均接触角，γ＝（αe＋αi）／2。

2 轴承动态性能分析

本文以某型号双列圆锥滚子轴承为例，轴承主参数见表1。结合双列圆锥滚子轴承动力学模型，采用精细积分法和预估－校正Adams-Bashforth-Mouhon多步法相结合的算法，对双列圆锥滚子轴承动力学微分方程进行积分求解，在此基础上，开发了双列圆锥滚子轴承动力学分析软件DTRB／HKD。

分析软件DTRB／HKD是以多体动力学软件ADAMS为平台，利用其自身宏命令对轴承建模进行的二次开发，并采用计算机编程语言编写轴承内部元件间的相互作用力子程序，实现程序与轴承实体模型的动态链接，进而对轴承进行动力学分析。图5是DTRB／HKD分析软件的轴承实体建模的部分界面。

假设轴承运行温度为 80℃，处于完全弹流油润滑状态。本文采用所开发的动力学分析软件DTRB／HKD，在转速为1 000 r／min，不同轴向预紧量△0，不同径向载荷Fr下，对双列圆锥滚子轴承进行动力学分析，可得到轴承内滚动体与内外滚道及大挡边间的最大接触压力、滚子打滑率、滚子歪斜角和轴承疲劳寿命等力学性能。

表1 轴承主参数

图5 软件DTRB／HKD的轴承实体建模界面

2.1 最大接触压力

图6和图7为滚子与滚道间的最大接触压力。从图6和图7中可以看出：随着轴向预紧量的增加，滚子与滚道间的最大接触压力呈先减小后增大的趋势；随着径向载荷的增加，最大接触压力随之增加，但是小轴向预紧量时，最大接触压力增大的幅度较大，大轴向预紧量时，最大接触压力增大幅度较小；最大接触压力取得最小值时，轴向预紧量随着径向载荷的增加而增大。这是由于随着轴向预紧量的增加，轴承受载区的滚子数不断增加，最大接触压力减小，轴承承载能力增大；当轴向预紧量增加到一定程度时，轴承的所有滚子受载，此时最大接触压力随轴向预紧量的增加就会不断增加。当轴向预紧量较小时，径向载荷的增加对轴承载荷分布影响较大，最大接触压力的增大幅度较大，而在大轴向预紧量时，结果反之。

图7 滚子与内滚道间的最大接触压力

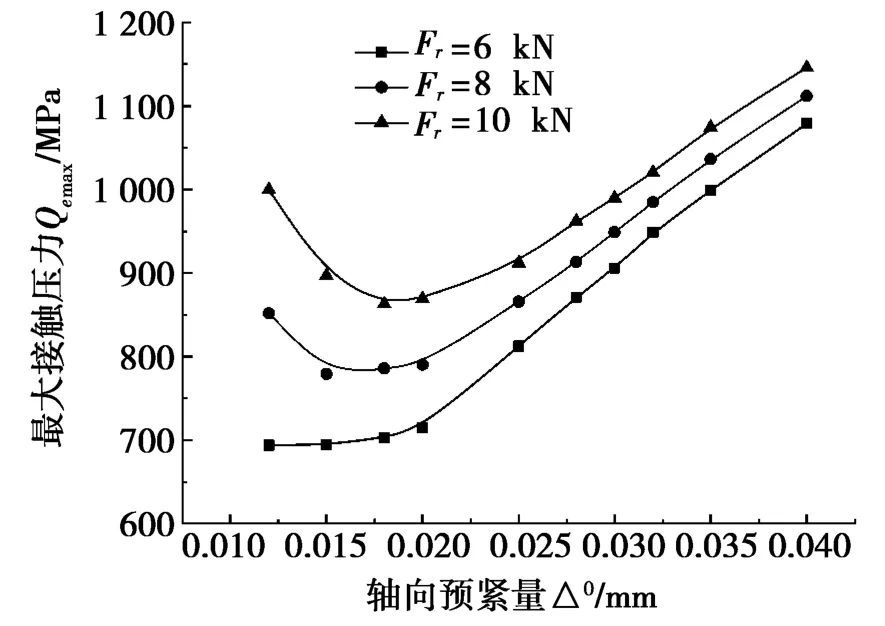
图6 滚子与外滚道间的最大接触压力

图8为滚子与大挡边间的最大接触压力。从图8中可以得到：随着轴向预紧量的增加，滚子与大挡边间的最大接触压力先减小后增大；在小轴向预紧量时，随径向载荷的增加最大接触压力不断增加，且增加幅度较大；大轴向预紧量时，随径向载荷的增加，最大接触压力增加不明显。这是由于轴向预紧量的增加，使滚子与大挡边接触的受载区增加，承载的滚子个数增加，滚子与大挡边间的最大接触压力减小；当轴向预紧量增加到一定程度，所有滚子与大挡边接触，最大接触压力随轴向预紧量的增加而增加。

2.2 滚子打滑率

图9为滚子打滑率随轴向预紧量及径向载荷的变化曲线。从图9中可以看出：双列圆锥滚子轴承滚子打滑率很小，基本在0.05%左右。在小轴向预紧量时，随着径向载荷的增加，滚子打滑率降低。这是由于滚子在滚道上运动时，滚子的线速度与滚道的线速度基本一致，使滚子在滚道上进行纯滚动运动。这也符合圆锥滚子轴承设计时，内外滚道延长线与滚子轴线相交于轴承轴线上点A（如图1所示），以实现纯滚动的目的。径向载荷的增加使滚子与滚道间的接触压力增加，滚子与滚道的摩擦增大，滚子打滑率降低。

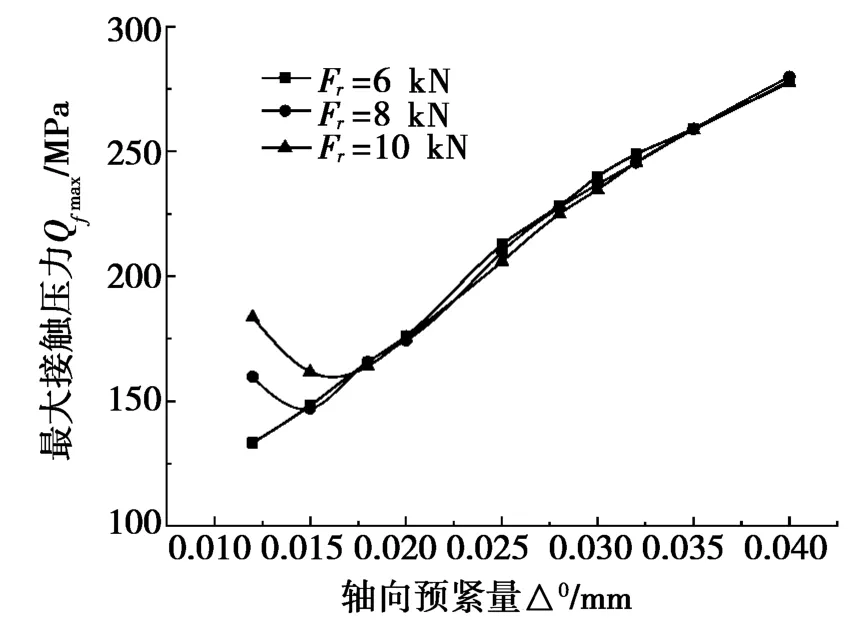
图8 滚子与大挡边间的最大接触压力

图9 滚子打滑率

2.3 滚子歪斜角

图10为轴承滚子歪斜角随径向载荷的变化规律。轴承运行过程中，会受到联合载荷的作用以及应用过程中内外圈轴线发生倾斜，这些都会导致摩擦力沿滚子长度分布不均匀，从而产生一个力矩使滚子发生歪斜，而滚子的歪斜角可以从所开发的仿真软件中测量得到。

从图10中可以看出：滚子歪斜角随着径向载荷的增加而增加，列1滚子的歪斜角略微大于列2滚子的歪斜角。这是由于径向载荷的增加，加剧了滚子所受的歪斜力矩，使滚子歪斜角增加。此分析中，轴承外圈承受一轴向载荷Fa＝1 kN，沿X轴负方向，使列1滚子处于“压紧”状态，列2滚子相比列1滚子处于“放松”状态，所以列1滚子上所受的歪斜力矩大于列2滚子，致使列1滚子歪斜角大于列2滚子歪斜角。

2.4 轴承疲劳寿命

图11为双列圆锥滚子轴承疲劳寿命曲线。轴承的疲劳寿命是轴承重要的性能，轴承的设计与应用都需要分析计算轴承的疲劳寿命。根据Lundberg和Plamgren的寿命计算方法得到双列圆锥滚子轴承的疲劳寿命计算公式：

式中，L10为轴承使用概率为90%时的疲劳寿命；a1为可靠性系数；a23为寿命修正系数；Qc为套圈额定滚动体负荷；Qe为套圈当量滚动体负荷。各参数的具体计算过程见文献［6］。

图10 滚子歪斜角

从图11可以看出：轴承疲劳寿命随着轴向预紧量的增加而增加直至达到最大值，随后迅速下降。轴承疲劳寿命取得最大值时最大接触压力取得最小值；轴向预紧量的最佳值随着径向载荷的增加而变大。当轴向预紧量取得过大（如0.04 mm）时，不仅不能增加轴承的承载能力，反而严重降低了轴承疲劳寿命。这可以为双列圆锥滚子轴承在实际使用过程中提供理论性指导，不同工况下双列圆锥滚子轴承的初始轴向预紧量都有一个最佳预紧量。

3 结论

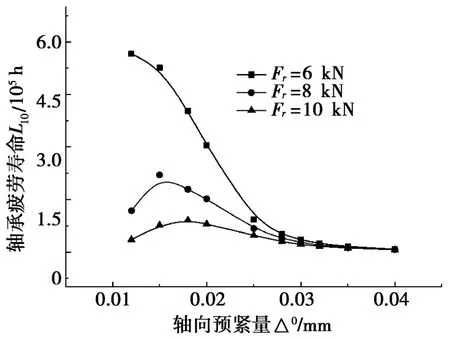
图11 轴承疲劳寿命

本文在滚动轴承动力学理论基础上，建立了双列圆锥滚子轴承动力学分析模型，采用精细积分法和预估－校正Adams-Bashforth-Mouhon多步法相结合的算法，求解轴承非线性动力学微分方程，针对双列圆锥滚子轴承的最大接触压力、滚子打滑率、滚子歪斜角以及轴承疲劳寿命等动态性能进行了研究，得出以下结论：

（1）轴承所受的最大接触压力随初始轴向预紧量的增加呈先减小后增大的趋势，最佳预紧量随外载荷的增加而变大。

（2）双列圆锥滚子轴承滚子打滑率较小，滚子运动基本处于纯滚动状态，这也符合圆锥滚子轴承设计的目的。

（3）滚子歪斜角随着径向载荷的增加而变大，并且“压紧”侧的滚子歪斜角略微大于“放松”侧。

（4）轴承疲劳寿命随轴向预紧量的增加先增大后减小。轴承疲劳寿命取得最大值时对应初始轴向预紧量有一最佳值，此结果与轴承最大接触压力特性相符合。

［1］ Walters C T.The Dynamics of Ball Bearings［J］.Trans ASME，Journal of Lubrication，1971，93（1）：1－10.

［2］ Gupta P K.On the Dynamics of a Taperd Roller Bearing［J］.Journal of Tribology，1989，111（2）：278－287.

［3］ Cretu S，Mitu N，Bercea I.A Dynamics Analysis of Tapered Roller Bearing Under Fully Flooded Conditions［J］.Wear，1995，188（1／2）：1－18.

［4］ 罗继伟，张俊杰.圆锥滚子接触应力数值求解［J］.轴承，2004（9）：1－3.

［5］ 张国方，卢红，柯常忠.圆锥滚子轴承负荷分布计算［J］.汽车运用，1996（4）：54－57.

［6］ 邓四二，贾群义.滚动轴承设计原理［M］.北京：中国标准出版社，2008.

［7］ 张凤琴，杜辉，邓四二，等.基于ADAMS的圆柱滚子轴承仿真分析［J］.河南科技大学学报：自然科学版，2009，30（2）：15－18.

［8］ 邓四二，付金辉，王燕霜，等.航空发动机滚动轴承-双转子系统动态特性分析［J］.航空动力学报，2013，28（1）：195－204.

［9］ Deng S E，Teng H F，Wang Y S，et al.Constitutive Equation of a New Aviation Lubricating Oil［J］.Chinese Journal of Mechanical Engineering：English Edition，2007，20（5）：28－31.

［10］ Kleckner R J，Pirvics J.High Speed Cylindrical Roller Bearing Analysis-SKF Computer Program CYBEAN，Vol.1：Analysis［R］／／King of Prussia：KF Industries Inc.，1978.

［11］ 胡浪，王文中，赵自强，等.双列圆锥滚子轴承滚子大端－引导边润滑接触分析［J］.摩擦学学报，2013，33（1）：22－28.

TH133.33

A

1672－6871（2014）06－0014－06

国家“十二五”科技攻关基金项目（JPPT-ZCGX1-1）；河南省科技创新杰出人才计划基金项目

胡广存（1989－），男，河南舞钢人，硕士生；邓四二（1963－），男，江苏丹阳人，教授，博士，博士生导师，主要研究方向为滚动轴承设计及理论.

2014－01－23