A Rule of Spatial Sampling on Cylindrical Shells for Predicting Radiated Acoustic Field

(School of Naval Architecture,Ocean and Civil Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

A Rule of Spatial Sampling on Cylindrical Shells for Predicting Radiated Acoustic Field

WANG Bin,TANG Wei-lin,FAN Jun

(School of Naval Architecture,Ocean and Civil Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

Structural borne acoustic radiation can be determined solely by the surface velocity distribution which is measured more easily than other physical quantities.The sampling intervals should be chosen carefully to ensure the prediction precision and reduce the system cost at the same time.In this paper,the prediction error with respect to the sampling intervals for the simply supported cylindrical shells is formulated as a mathematical problem,in which the sampling intervals needed in axis and in circumference can be studied separately.The rules for the determination of the sampling intervals to satisfy certain predetermined criteria are put forward.The sampling interval in axis is just determined by the axial order of the mode and a dimensionless quantity;in circumference it is mainly decided by the circumferential order and another dimensionless quantity.In the cases of finite circumferential modes,the number of the sampling points in circumference is only determined by the highest order of these modes.

structural borne sound;radiation prediction;sampling interval

Biography:WANG Bin(1981-),male,Ph.D.student of Shanghai Jiao Tong University.

1 Introduction

In an infinite fluid,the structural borne acoustic radiation can be solely determined by the surface velocity distribution.Considering it can be measured easier than other physical quantities,people have devoted themselves to the numerical methods[1-2]based on the surface velocity distribution,among which Boundary Element Method(BEM)is most widely used.In order to improve prediction precision and calculation speed,people pay attention mainly to improving the numerical methods[3-4].All of them assume the surface velocity distribution is known.However,this simple assumption requires the vibration sensors be distributed on the whole surface,which is very difficult or even impossible to be implemented in most practical applications.

Besides the coarse requirement of six samples per acoustic wavelength in BEM[5],these are few open papers discussing the surface spatial sampling interval in predicting the structural borne acoustic radiation.Ref.6 discussed the rule for the determination of sampling interval on rectangular plates with respect to the analyzing frequency,the error range,the mode order,and the observer elevation.Considering cylindrical shells are more representative than rectangular plates in analogy with actual underwater vehicles,the rule for the determination of sampling intervals satisfying the prediction error requirement for simply supported baffled cylindrical shells is discussed in this paper.

2 Radiation theory based on simply supported baffled cylindrical shells

Considering a simply supported cylindrical shell with length L,radius a and semi-infinite rigid cylindrical baffles at the ends as shown in Fig.1,the normal velocity on the surface of the cylindrical shell can be expressed as a sum of many modes[7]

where m is the axial order and n is the circumferential order of these modes.

The assumption of semi-infinite cylindrical baffles endows the acoustic field of the finite cylindrical radiators with an analytical expression.Transformed from the cylindrical coordinates to the spherical coordinates and calculated with the stationary phase method,the acoustic pressure for a remote observer point R,θ,( )φ radiated from each moden,( )m can be expressed analytically as[8]

in the above equations,ρ0is the density of the fluid,c0is sound speed in the fluid,k0is wave number,(·) is the first derivative of the first kind of nth order Hankel function and the time dependence is always assumed as e-jωt.

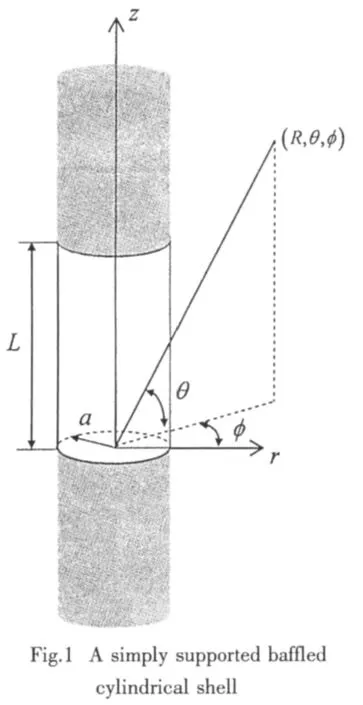
3 An efficient prediction method for radiated acoustic field

Nowadays,BEM is the most widely used numerical method and available for arbitrary boundary geometries theoretically.Another efficient numerical method is adopted here,which is easier to be implemented than BEM in evaluating the prediction error with respect to the sampling intervals.

Suppose the number of the sampling points in axis is M and that in circumference is N,and then the acoustic pressure radiated by a single mode n,( )m can be written as

where zj=(2j - 1) L/2M,φi=(2i - 1) 2π/2N are the axial coordinate and the circumferential coordinate of the (i, j ) th sampling point respectively, υnm(zj, φi)is the normal velocity at the(i, j ) th sampling point

and pij(R ,θ ,φ )denotes the acoustic pressure at the observer point(R ,θ ,φ )radiated by the baffled conformal piston centered at the (i, j ) th sampling point and vibrating in unit velocity[8]

where 2L0=L/M is the axial length of the piston,2α0=2π/N is the circumferential angle of the piston and j0(·) is the zero-order spherical Bessel function.When the piston is very small compared to the cylindrical shell,these two factors j0(k0L0cos θ)and j0(tα0)in Eq.6 can be approximated as 1.

Eq.4 can be rewritten as

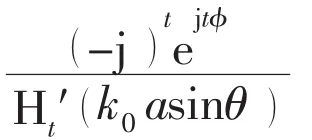
Considering the cases of M→∞,N→∞,the limits of Eqs.8 and 9 can be obtained,

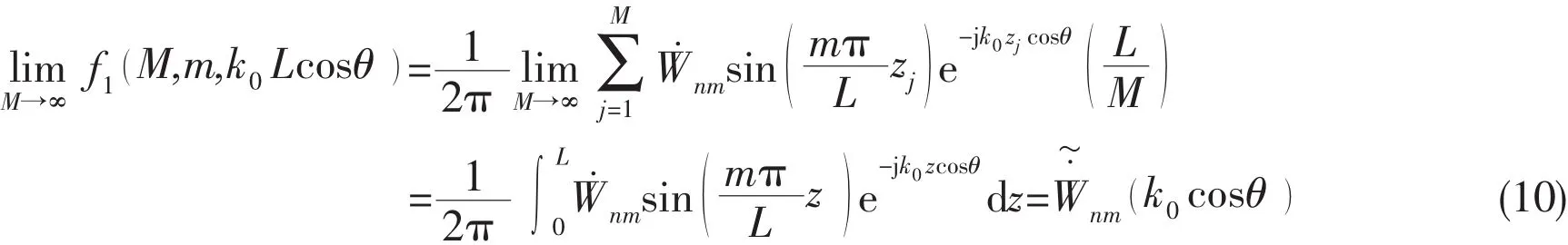
So,it can be proved that Eq.7 is convergent to the analytical expression with the number of sampling points trending to infinity

that is,the sampling intervals in axis and in circumference are fine enough.The prediction error is formulated as the same as that in Ref.[6]

This is a complicated function which is related with the order of the mode,the sampling intervals,the observer orientation and the analyzing frequency.According to Eq.7,the prediction error can be rewritten as

Given an intended error,the number of sampling points needed in axis is just decided by the axial order,and the dimensionless quantity k0Lcosθ,and that in circumference is determined by the circumferential order,the dimensionless quantity k0asinθ,and the observer azimuth φ.

In the above,the prediction error with respect to the sample intervals for the simply supported cylindrical shells has been formulated as a mathematical problem,that is,the balance between the number of the integral points and the integral precision for these two functions in Eqs.8 and 9.It is notable that there is a great difference between these two functions in form.It can be directly explained that the axial curvature and the circumferential curvature are quite different from each other.Besides that,the non-zero curvature makes the rule of spatial sampling on cylindrical shells quite different from that on rectangular plates,especially squarelike plates which can be sampled equally in the directions parallel with the sides[6].

4 Spatial sampling for the simply supported cylindrical shell

It is impossible to reveal the relationships between the number of the integral points and the integral precision for these two functions f1(M,m,k0Lcos θ) and f2(N,n,k0asinθ,φ )analytically.So numerical analysis is adopted in this section.The rules for the determination of the sampling intervals in axis and in circumference to satisfy certain predetermined criteria are investigated separately.

4.1 Spatial sampling in axis

The form of function f1(M,m,k0Lcos θ)reveals that prediction error with respect to sampling number M in axis is just determined by the axial order m and the dimensionless quantity k0Lcosθ decided by the observer point and the analyzing frequency.Assuming the intended error is 0.1dB,the relationships between the number of sampling points needed and the dimensionless quantity k0Lcosθ are shown in Fig.2.

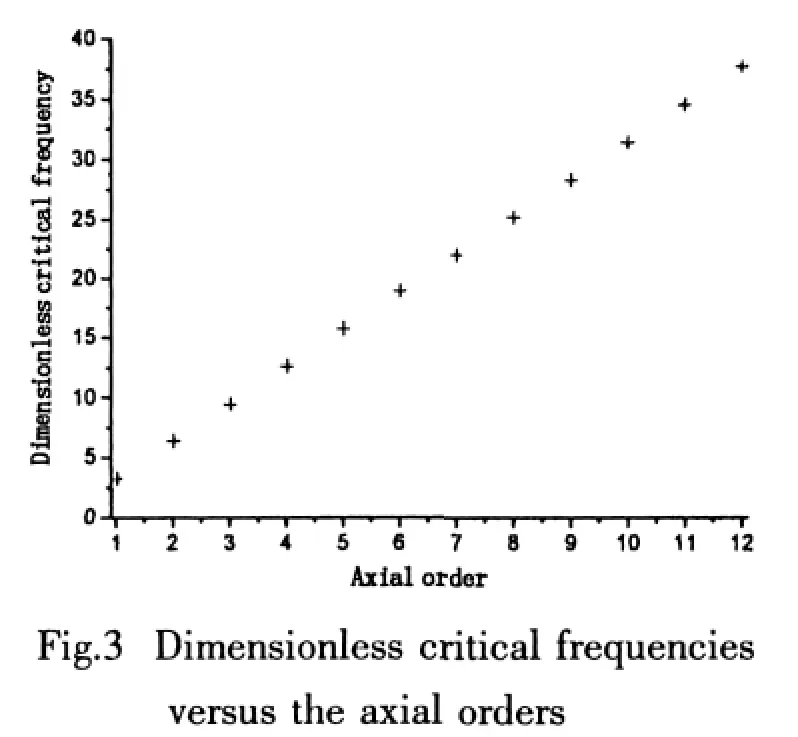
It can be seen that there is a dimensionless critical frequency Fafor each mode as that in case of plates[6],which is related with the axial order.When the observer point and the analyzing frequency satisfy k0Lcosθ≤Fa,the number of sampling points needed changes slowly with the dimensionless quantity k0Lcosθ.When Fais exceeded,the number of sampling points needed increases with k0Lcosθ,the linear slope nearly independent of the axial order m.Therefore,this dimensionless critical frequency Faplays an important role in lessening the sampling points and ensuring the prediction precision at the same time.It is necessary to find out the relationship between the exact values of Faand the axial orders m.The relevant results are shown in Fig.3 with the intended error 0.1dB.

It is obvious that the dimensionless critical frequency Fafor each mode increases linearly with the axial order and can be approximated as

This approximation is not obtained occasionally and has been explained in Eq.8 implicitly.The wavenumber spectrum of the discrete spatial sampling is a result of periodic superposition of the spectrum of the analogous spatial signal.The prediction error defined in Eq.15 is decided by the relative error of the aliasing interference at the specific argument k0cosθ.With a fixed sampling interval,the aliasing interference is weakened to the utmost extent at the wavenumber of the spectrum peak.In other words,given a fixed intended error,the number of sampling points needed is the most least when this specific argument k0cosθ approaches the wavenumber of the spectrum peak.

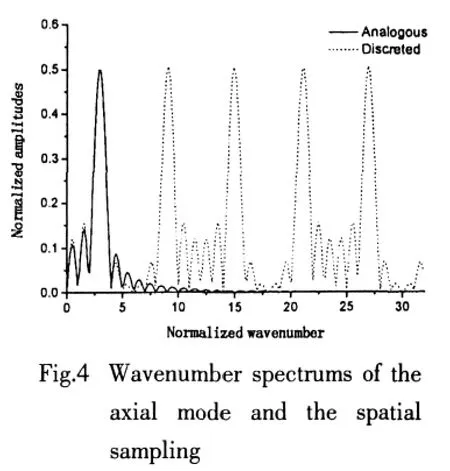
To make clear of the explanations for Figs.2 and 3,a certain axial mode is taken as an example.The wavenumber spectrum can be expressed as

and shown in Fig.4,together with the spectrum of the discrete spatial sampling.

The axial order m and the number of the sampling points M are set as 6 and 12 respectively.And the amplitudes of spectrum and the wavenumber are both normalized with L/2π.It can be seen that the spectrum peak is in the neighborhood of the wavenumber K1=mπ/L.When the observer point and the analyzing frequency satisfy k0cosθ≈K1,that is k0Lcosθ≈mπ,the number of the sampling points in axis is the most least for a fixed intended error.With the disparity between k0Lcosθ and mπ increasing,the aliasing interference becomes stronger as a result of the wavenumber spectrum descending,and the number of sampling points in axis has to be increased to satisfy the fixed intended error.

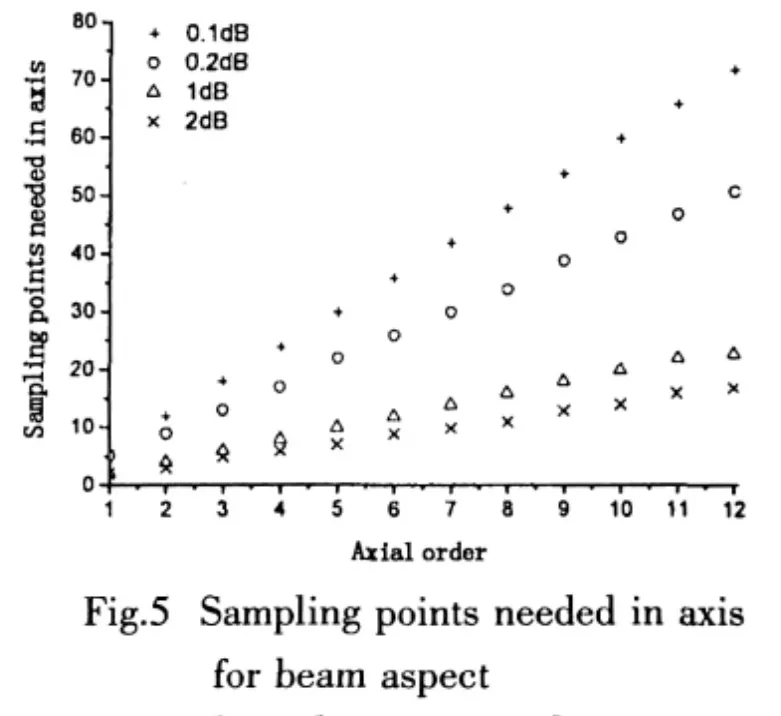
In some fields,the observer elevation θ close to 90°often catches more attentions than other observer elevations,which is called as beam aspect.The numbers of the sampling points in axis required by the different intended errors for k0Lcosθ→0 are shown in Fig.5.

It is obvious that the number of the sampling points needed in axis is proportional to the axial mode,the linear slope increasing with the prediction precision.The number of the sampling points can be approximated as the integer close to

where A0erris a coefficient related with the prediction precision and listed in Tab.1 with the fitting method.

Tab.1 Fitting values of A0errwith respect to the intended errors

In the case of the observer point and the analyzing frequency satisfying k0Lcosθ＞＞Fa,the number of the sampling points needed in axis versus the dimensionless quantity k0Lcosθ is discussed in Fig.6,with the axial order m=2.For the linear slope changes little with the axial order m,the conclusions drawn in Fig.6 are also correct for other axial orders m≠2.

In Fig.6,the linear slope of the number of the sampling points in axis versus k0Lcosθ de-pends on the intended errors strongly which can be approximately presented as

where Aerris a coefficient increasing with the prediction precision.In other words,the sampling interval in axis to satisfy the intended error can be expressed as

where λ0is wavelength of sound in fluid.The fitting values of Aerrwith respect to the intended errors are listed in Tab.2.

Tab.2 Fitting values of Aerrversus the intended errors

For the observer point near the ends of cylindrical shellscosθ→()1,the requirement of

the sampling interval in axis is strictest

4.2 Spatial sampling in circumference

The form of function f2(N,n,k0asinθ,φ )indicates that the prediction error with respect to the circumferential sampling is determined not only by the circumferential order n and the dimensionless quantity k0asinθ,but also by the observer azimuth φ.Given a further consideration on Eq.15,it can be obtained that

that is,the prediction error with respect to the observer azimuth φ is periodic with.When N is large enough,the dependence on the observer azimuth φ can be neglected and the prediction error is mainly determined by the circumferential order n and the dimensionless quantity k0asinθ.

Assuming the intended error is 0.1dB and the observer azimuth φ=0,the numbers of the sampling points needed in circumference versus the dimensionless quantity k0asinθ are shown in Fig.7.

It can be seen that the number of the sampling points in circumference is just decided by the circumference order n

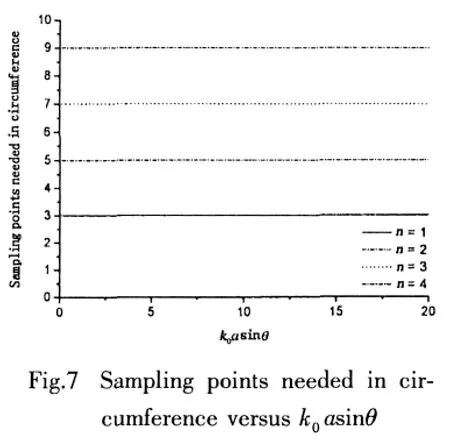
and independent of the dimensionless quantity k0asinθ.Another surprise is that the prediction error defined in Eq.16 is 0dB.On another view,this result can be understood easily.In the cases of finite modes in circumference,all the information of these modes can be recovered precisely from the spatial sampling as long as the number of the sampling points in circumference is higher than the highest order of these modes two times,and then the acoustic radiation can also be known.

However,it must be born in mind that the prediction error with respect to the sampling interval in circumference is no longer 0dB in the cases where there are infinite modes in circumference,such as a patch excitation considered.And the number of the sampling points needed in circumference is also related with the dimensionless quantity k0asinθ.The higher prediction precision designated or the larger k0asinθ concerned,the more sampling points in circumference are required.

5 Conclusions

In this paper,spatial sampling on the cylindrical shells for predicting radiated acoustic field has been investigated.The prediction error with respect to the sampling intervals for the simply supported cylindrical shells has been formulated as a mathematical problem,that is,the balance between the number of the integral points and the integral precision for two separable functions.Some conclusions have been drawn as follows.

(1)Prediction error with respect to the sampling interval in axis is determined by the axial order and the dimensionless quantity k0Lcosθ.There is a dimensionless critical frequency Fafor each mode,which equals the product of the axial order and π.If the observer point and the analyzing frequency satisfy k0Lcosθ≤Fa,the number of the sampling points needed in axis changes slowly with k0Lcosθ.Otherwise,it increases linearly with k0Lcosθ and the sampling interval in axis approximates λ0/2Aerrπcosθ.For the beam aspect,the number of the sampling points in axis is mainly determined by the axial order,the linear slope increasing with the prediction precision.

(2)Prediction error with respect to the sampling interval in circumference is decided by the circumferential order,the dimensionless quantity k0asinθ and the observer azimuth.When the sampling points are sufficient,the observer azimuth dependence can be neglected.In the cases of finite modes in circumference,the number of the sampling points in circumference is just required to be higher than the highest circumferential order two times.

[1]Chertock G.Sound radiation from vibrating bodies[J].J Acoust.Soc.Am.,1964,36(7):1305-1313.

[2]Chen L H,Schweikert D G.Sound radiation from an arbitrary body[J].J Acoustic.Soc.Am.,1963,35(10):1626-1632.

[3]Schenck H A.Improved integral formulation for acoustic radiation problems[J].J Acoust.Soc.Am.,1968,43:44-51.

[4]Koopmann G H,Song L,Fahnline J.A method for computing acoustic fields based on the principle of wave superposition[J].J Acoust.Soc.Am.,1989,86(5):2433-2438.

[5]SYSNOISE Rev 5.5:User manual[K].LMS International,2000.

[6]Tao J,Ge H,Qiu X.A new rule of vibration sampling for predicting acoustical radiation from rectangular plates[J].Applied Acoustics,2006,67(8):756-770.

[7]Laulagnet B.Model analysis of a shell’s acoustic radiation in light and heavy fluids[J].J of Sound and Vibration,1989,131(3):397-415.

[8]Junger M C,Feit D.Sound,Structures,and Their Interaction[M].Cambridge MA:MIT Press,1986.

[9]Szechenyi E.Modal density and radiation efficiencies of unstiffened cylinders using statistical method[J].J of Sound and Vibration,1971,19(1):65-68.

[10]Mclean R F,Alsop S H,Fleming J S.Nyquist-overcoming the limitations[J].Journal of Sound and Vibration,2005,280:1-20.

基于辐射声场预报的圆柱壳表面空间采样研究

王 斌，汤渭霖，范 军

（上海交通大学船舶海洋与建筑工程学院，上海200240）

无限流体介质中振动结构的辐射声场可以由其表面振速分布唯一地确定，而且表面振速相对于其它物理量而言更容易被可靠测量。然而，必须谨慎选择表面振速的空间采样间隔，以确保预报声场精度较高，同时预报系统负担较小。文中讨论了简支圆柱壳表面振速的空间采样问题，将采样间隔与预报误差之间的关系简化为一个数学问题，其中周向采样问题与轴向采样问题可以分离、单独研究。总结了在指定预报精度范围内表面振速空间采样的有关规律：轴向采样点数取决于轴向模态阶次以及一个无因次量；周向方向采样点数主要取决于周向模态阶次以及另一个无因次量。对于周向模态有限的情况，周向采样点数仅取决于周向模态的最高阶次。

结构声辐射；辐射声场预报；采样间隔

O427.5

A

王 斌（1981-），男，上海交通大学船舶海洋与建筑工程学院博士研究生；

范 军（1973-），男，上海交通大学船舶海洋与建筑工程学院教授，博士生导师。

O427.5

A

1007-7294（2010）06-0690-09

date：2009-05-08

汤渭霖（1940-），男，上海交通大学船舶海洋与建筑工程学院教授，博士生导师；