高围压下高孔隙水压对岩石蠕变特性的影响

蒋海飞,刘东燕,黄 伟,刘芳语

(1.重庆大学土木工程学院,重庆 400045;2.煤矿灾害动力学与控制国家重点实验室(重庆大学),重庆 400044)

高围压下高孔隙水压对岩石蠕变特性的影响

蒋海飞1,2,刘东燕1,黄 伟1,刘芳语1

(1.重庆大学土木工程学院,重庆 400045;2.煤矿灾害动力学与控制国家重点实验室(重庆大学),重庆 400044)

为研究高应力作用下深部岩体开挖过程中孔隙水压对围岩时效变形特性的影响,选取重庆某深部细砂岩为研究对象,对其进行不同水压下分级加载蠕变试验,试验表明:孔隙水压增强了砂岩的变形能力,但随着水压的升高,加载初期的一段时间内,水压在一定程度上会延缓轴向变形;蠕变过程中黏弹性模量随时间呈指数函数变化,通过分析不同水压作用下指数函数中参数的变化规律,得到黏弹性模量随时间和水压变化的表达式,进而提出修正的广义Kelvin模型,该模型能较好的描述不同水压作用下岩石的非线性黏弹性蠕变特性。基于不同水压下加速蠕变试验曲线特征,采用拟合、类比的方法引入一个能反映不同水压作用时加速蠕变特征的二元件黏塑性模型,将该模型与修正的广义Kelvin模型串联组成一个新的非线性黏弹塑性蠕变模型。基于试验结果,利用优化分析软件1stOpt,对模型参数进行辨识,效果比较理想;对比试验曲线和理论曲线,二者吻合较好,验证了模型的正确性。

高围压;高孔隙水压;细砂岩;蠕变模型

蠕变是岩石的重要力学性质之一,大量工程实践表明,岩石蠕变是工程产生大变形乃至失稳的重要原因之一[1-2]。众多国内外学者对岩石的蠕变进行了大量研究,取得了许多成果[3-11]。

近年来随着开采向深部发展,开采过程中的工程灾害不断增多,使得巷道的开挖、支护以及维护等问题越发显得突出,特别是受高应力和高压水体的威胁越来越严重,高应力高水压使得围岩的结构和力学性能恶化,实际载荷高于表观载荷,岩体的蠕变变形大大增加。正因如此,目前我国煤炭行业频繁发生矿井突水事故,给企业带来巨大的经济损失和人员伤亡。岩土工程发生突水的实质是岩体在水压和外力共同作用下发生蠕变破坏[12]。因此加强对高应力高水压作用下岩石蠕变特性的研究,不仅可以加强对复杂环境下岩体流变规律的进一步认识,还能为岩土工程的设计、施工和运行提供更全面、更可靠的基础资料。目前,有关高围压高水压条件下岩石蠕变特性研究的成果相对较少。

基于此,本文对重庆某深基坑细砂岩进行高围压高水压作用时的三轴压缩蠕变试验,分析了蠕变特性;通过研究不同水压下等时应力-应变曲线,得到一个修正的广义Kelvin模型;根据加速蠕变试验曲线特性,提出非线性黏塑性加速蠕变启动模型,将二者串联,构建一个新的非线性黏弹塑性蠕变模型。

1 蠕变试验及其成果分析

试验采用RLW-2000岩石三轴流变试验系统。试验所需岩样取自重庆地区某深基坑细砂岩,主要成分为石英、长石、燧石和白云母等。依据国际岩石力学学会(ISRM)试验规程对岩样进行加工,制成直径50 mm、高度100 mm的圆柱体。试样干密度为2.33～2.74 g/cm3,孔隙率为0.63%～0.71%,粒径为0.01～0.50 mm,单轴抗压强度为63.40 MPa,弹性模量为25.03 GPa,泊松比为0.13。需施加孔隙水压的试样在真空抽气饱水机中饱和24 h,再放入水中浸泡7 d。共进行5种工况下的三轴压缩蠕变试验(表1)。试验加载过程采用轴向应变控制,试验加载速率为0.01 mm/s。为方便比较分析,在轴向偏压加载过程中,保证每级轴向偏压力水平相等,并尽量使每级加载延续时间也对应相等。

试验前,利用MTS815岩石力学测试系统对5种工况下的岩样进行了三轴压缩强度试验。为保证测试数据的一致性,每种工况选取3个岩样进行强度测试,并取其平均值,见表2。

表1 三轴蠕变试验工况Table 1 W ork conditions of triaxial creep test

表2 细砂岩三轴压缩试验结果Table 2 Test results of fine sandstone under triaxial com pression

试验中,观察第1级应力水平达到设定值时的应变值和强度试验结果作比较,若相差较大,说明试件均匀性不够,不能保证力学性能的一致性,予以舍弃。换下一组试件继续试验。5种工况下分级加载三轴压缩蠕变试验曲线如图1所示。各级加载应力水平(σ1-σ3)标识在曲线上方。

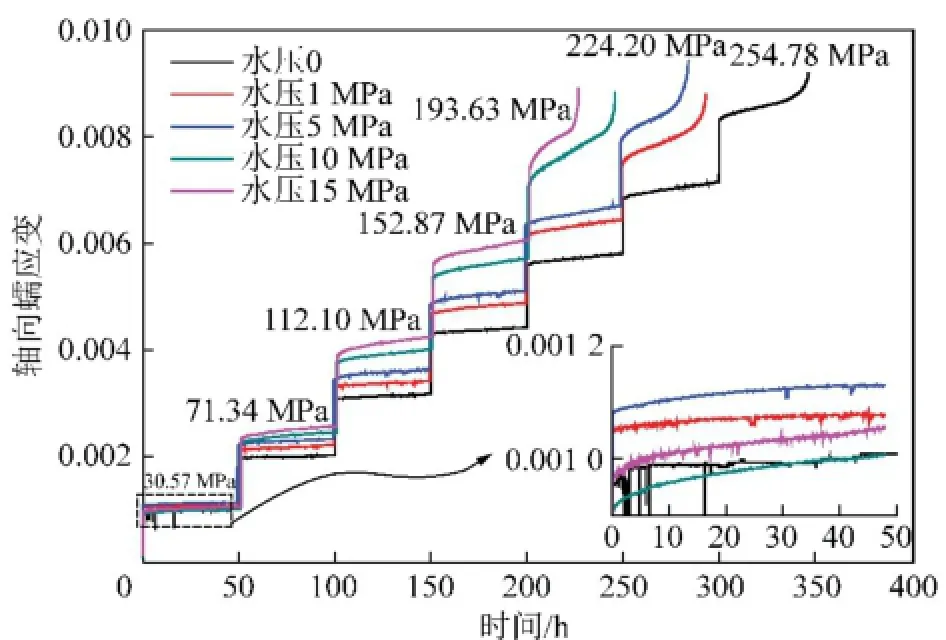
图1 不同水压下砂岩分级加载蠕变曲线Fig.1 Creep strains under differentwater pressure

由图1可知,相同应力水平作用下,随着水压的增大,蠕变破坏时间逐渐缩短,岩样的变形能力明显增大,最终破坏的偏应力也逐渐降低。最后一级应力水平下,水压为0的岩石试件加速蠕变曲线较为缓和,而随着水压的增大,加速蠕变曲线明显变得较为陡峭,当水压为15 MPa,偏应力增至193.63 MPa时,经历一段时间的蠕变后,突然破坏,稳定蠕变到加速蠕变的过度段不再明显,岩石破坏呈现出脆性破坏的特征。

对第1级应力水平作用下的蠕变曲线放大(图1中小图),发现水压10 MPa的蠕变曲线位于最下方,并随着时间的推移,逐渐靠近无水压作用时的蠕变曲线;水压15 MPa的蠕变曲线虽位于无水压作用的蠕变曲线上方,但其蠕变量却低于水压为1和5MPa的试样的蠕变量。

除了考虑材料本身的离散性以及试验过程中的误差会导致上述现象,笔者分析认为,蠕变试验加载初期,应力水平较低,岩石内部孔隙大都处于相互隔绝状态或是通过极微小的裂隙连结,且受到高围压的限制,孔隙水排出极为缓慢,孔隙水会在裂纹面上产生一个反向的抵抗作用,延缓轴向变形,即短时间内含孔隙水压力的试件变形模量有所提高。文献[11]也得到相似结论。

另一方面,孔隙水压也会在孔隙的裂纹尖端形成一个附加的拉力,增强裂纹的扩展能力,随着裂纹的不断扩展,原生孔隙间不断连通,连结孔隙的裂纹在应力作用下也不断增大,水被挤压排出孔隙的速度加快,孔隙水压抵抗轴向变形的能力将逐渐减弱直至消失,此后,岩石强度不断劣化,岩石中孔隙水转而起到促进岩石变形的作用。

通过对分级加载蠕变试验曲线进行处理[2],可得到不同水压下岩样的等时应力-应变曲线(图2)。本文仅讨论由蠕变阶段构成的关系曲线,而忽略瞬间加载过程。由图2可知,不同时刻应力-应变曲线形状非常相近;随着应力增长,同一时刻曲线斜率不断变小,非线性特征愈加明显。但水压的增大使得这种非线性特征逐渐减弱,如图2(d),(e)所示,各阶段曲线斜率变化相对较低水压时的变化很小。此外,随着时间推移,曲线的斜率逐渐降低,且水压的增大会导致降低程度愈加明显。

图2 等时应力-应变曲线Fig.2 Isochronous stress-strain curves

当应力水平低于屈服应力时,蠕变主要表现为黏弹性变形,Kelvin元件模型可以描述这种蠕变特性。此外,等时应力-应变曲线中的近似直线段正是反映了不同时刻岩石的黏弹性变形特性。因此,将等时应力-应变曲线中的近似直线段的斜率定义为蠕变黏弹性模量。通过计算图2不同水压不同时刻近似直线段的斜率,得到各时刻蠕变黏弹性模量,获得不同水压下蠕变黏弹性模量与时间的关系,如图3所示。

根据图3不同水压下蠕变黏弹性模量与时间关系的数据分布,可以用非线性拟合的方法得到二者之间相互关系的函数表达式:

图3 黏弹性模量与时间关系Fig.3 Relation betweenmodulus of visco-elasticity and time

式中,A,B为拟合参数。

假设初始时刻黏弹性模量为E0,当t=0时, E(t)=A,令A=E0,则

这就建立了初始黏弹性模量与后续时刻黏弹性模量之间的关系。且从损伤力学角度来看,建立初始时刻与后续时刻蠕变参数之间的关系能够反映材料特性随时间的劣变过程。

由表3可知,不同水压下拟合参数发生了不同程度的变化:A值变化幅度在0.91%～20.55%;而B值增大幅度为19.10%～66.29%。可见,水压对B值的影响非常明显,对A值的影响相对较弱。为了简化问题,主要考虑不同水压对B值的影响,寻求B值随水压变化的规律,进而得到蠕变黏弹性模量随时间和水压变化的函数表达式。

表3 E(t)=A exp(-Bt)拟合结果Table 3 Fitting resu lts of E(t)=A exp(-Bt)

根据图4,B值与水压数据分布特点,利用式(3)对其进行拟合,对应的拟合参数γ,φ分别为0.000 99和0.024 6,参数拟合相关系数平方R2为0.906 58,则

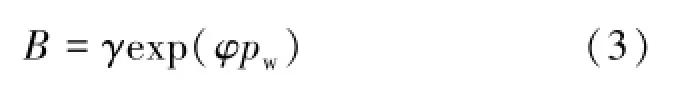
式中,pw为孔隙水压力。

图4 B数据分布及拟合曲线Fig.4 Data distribution and fitting curve of B

将式(3)代入式(2),便可得到蠕变黏弹性模量随时间和水压变化的函数表达式为

2 修正的广义Kelvin模型

当应力水平低于屈服应力,采用广义Kelvin模型描述细砂岩的蠕变变形过程时,假定Kelvin模型中的弹簧体变形模量E符合式(4)的函数关系,则可得到修正的广义Kelvin模型,如图5所示。

该模型的状态方程为

图5 修正的广义Kelvin模型Fig.5 Revised Kelvinmodel

式中,σ1,σ2和ε1,ε2分别对应图5中1,2部分的应力和应变;E1,E(E0,B0,pw,t)为岩石材料的弹性参数;η2为岩石黏性参数。

3 高围压、高水压下非线性黏弹塑性模型

3.1 高围压、高水压下非线性黏塑性模型

传统的元件模型无法描述具有非线性特征的加速蠕变阶段,而加速蠕变是岩石破坏的关键环节,因此有必要对高围压高水压作用下加速蠕变阶段的非线性特征作进一步研究。加速蠕变阶段,应变与时间成非线性关系,元件模型中,用来表示应变-时间关系的为黏性元件,因此可以用非线性黏性元件代替模型中线性黏性元件[5],基于这样的思想,参照文献[13]先用经验公式对不同水压下加速蠕变段曲线进行拟合,再通过类比的方法得到一个在不同水压作用下随时间呈现非线性变化的黏滞系数η,进而提出一个非线性黏性元件,并采用应力触发方式,将其与塑性元件并联,组成一个新的非线性黏塑性模型。

首先,采用幂函数对不同水压作用下细砂岩三轴压缩加速蠕变曲线进行拟合,其表达式为

式中,ε0为加速蠕变之前的应变值;C为拟合参数;n为加速蠕变指数。

图6为加速蠕变段曲线与理论曲线的对比,其拟合参数见表4,参数拟合相关系数平方均达到了0.96以上,因此采用幂函数对加速蠕变曲线进行拟合是合适的。

图6 加速蠕变曲线与理论曲线Fig.6 Comparison between theoretical curve and accelerate creep curve

由表4可知,ε0变化不大;C值变化幅度很大,且没有明显的规律性。n值随水压的增加而增大,有较为明显的变化规律。故主要考虑水压对加速蠕变指数n的影响。

表4 ε=ε0+Ctn拟合结果Table 4 Fitting results ofε=ε0+Ctn

图7为n值的数据分布,通过观察数据分布特点,采用线性方程式(9)对其进行拟合,对应的拟合参数a=9.855 96,b=1.265 2,参数拟合相关系数平方R2=0.955 44,拟合效果比较理想。n=a+bpw(9)式中,a,b为拟合参数。

图7 n数据分布及拟合曲线Fig.7 Date distribution and fitting curves of n

假设水压为0时,加速蠕变指数为n0,将pw=0代入式(9),得n=a=n0,则

式中,n0为无水压时加速蠕变指数,根据无水压状态时加速蠕变指数n0来推求不同水压下加速蠕变指数,反映了加速蠕变过程中水压对岩石的劣化作用。

将式(10)代入式(8)得到加速蠕变阶段蠕应变随时间和水压变化的函数表达式:

在线性黏塑性元件模型中,当σ＞σs时,其蠕变方程为

经上述非线性处理后得到的非线性黏塑性模型如图8所示。

图8 非线性黏塑性模型Fig.8 Nonlinear visco-plasticmodel

模型可以反映细砂岩在不同应力水平和水压下的加速蠕变特征,其相应的蠕变本构方程可表示为

3.2 高围压、高水压下非线性黏弹塑性蠕变模型

将修正的广义Kelvin模型与非线性黏塑性模型串联得到如图9所示的非线性黏弹塑性蠕变模型。

在图9的元件模型中,当σ＜σs时,非线性黏滞系数牛顿体不起作用,仅有1,2部分参与蠕变,此时蠕变模型即为修正的广义Kelvin模型,其蠕变方程见式(7)。

图9 非线性黏弹塑性蠕变本构模型Fig.9 Nonlinear viscoelastic p lastic creep constitutivemodel

在岩土工程中,岩土体大多处于三维应力状态,本文也是通过室内三轴压缩蠕变试验成果对模型进行验证。因此,有必要建立三维应力状态下岩石蠕变方程。

假设岩石为各向同性体,三维应力状态下,将岩石内部的应力张量分解为σm和Sij,其表达式[1]为

一般认为,球应力张量σm只能改变物体体积;而偏应力张量Sij只引起形状变化。因此也可以将应变张量分解成球应变张量εm和偏应变张量eij,表达式如下[2]:

为了简化问题,假设材料的蠕变仅由偏应力张量引起[2],结合前面各式可得三维应力状态下蠕变方程:

4 模型参数识别及验证

在进行模型参数识别之前,先利用Boltzmann叠加原理,将图1分级加载条件下的蠕变曲线转化为分别加载条件下的蠕变曲线(图10)。限于篇幅,仅对围压40 MPa、水压为0和围压40 MPa、水压15 MPa工况下的蠕变曲线进行参数辨识。

根据蠕变试验得到的蠕变曲线,选择合适的方法对蠕变模型中的参数进行辨识,得到合理的模型参数。目前,较为普遍的做法是采用最小二乘法对蠕变曲线进行拟合,进而确定模型参数[13]。然而最小二乘法在解决非线性问题时,效果并不理想,若迭代的初始值选取不合理则会导致最终结果不收敛,或者收敛于局部极小点,且收敛速度比较慢[14]。

图10 蠕变试验曲线与理论曲线对比Fig.10 Comparison between creep test curves and theoretical curves

基于试验结果,利用1stOpt数学优化分析软件[15],对模型参数进行辨识。该软件的核心是通用全局优化算法(universal global optimization),其最大特点是克服了优化计算领域中使用迭代法必须给出合适初值的难题,即用户勿需给出参数初始值,而由软件随机给出,通过其独特的全局优化算法,最终找出最优解。在应力水平低于或高于屈服应力时,分别采用式(23)和式(24)对试验曲线进行拟合,得到的相关参数见表5,模型参数拟合相关系数平方均达到0.92以上,拟合效果比较理想。

表5 非线性蠕变模型参数Table 5 Parameters identification of nonlinear creep mode

图10为2种工况下蠕变试验曲线和理论曲线的对比,由图可见二者较为吻合,既显示数学优化软件1stOpt非线性拟合功能的强大,也表明提出的修正广义Kelvin模型和非线性黏弹塑性模型能够很好地反映细砂岩在高围压下,不同水压作用时的衰减蠕变、稳定蠕变和加速蠕变特征。验证了本文提出模型的正确性和适用性。

5 结 论

(1)高围压下,高孔隙水压的存在增强了砂岩的变形能力,但在加载初期的一段时间内,水压在一定程度上会延缓轴向变形。

(2)通过对高围压下,不同孔隙水压作用时细砂岩等时应力-应变曲线近似直线段斜率变化规律的研究,得到蠕变黏弹性模量随时间呈指数函数变化,再通过分析不同水压作用时指数函数中参数的变化规律,建立了黏弹性模量随时间和水压变化的表达式;进而提出修正广义Kelvin模型,该模型能较好的描述不同水压作用下岩石的非线性黏弹性蠕变特性。

(3)基于不同水压作用下加速蠕变试验曲线特性,采用拟合、类比的方法引入一个能反映不同水压作用下加速蠕变特征的二元件黏塑性蠕变模型,将该模型与修正的广义Kelvin模型串联组成一个新的非线性黏弹塑性蠕变模型。该模型可以描述岩石在不同应力水平作用和不同水压作用时的衰减蠕变、稳定蠕变和加速蠕变。

(4)根据试验结果,利用优化分析软件1stOpt,对模型参数进行辨识,效果比较理想;对比试验曲线和理论曲线,二者吻合较好,验证了模型的正确性和适用性。

[1] 蔡美峰,何满潮,刘东燕.岩石力学与工程[M].北京:科学出版社,2009:307-308.

Cai Meifeng,He Manchao,Liu Dongyan.Rock mechanics and engineering[M].Beijing:Science Press,2009:307-308.

[2] 孙 钧.岩土材料流变及其工程应用[M].北京:中国建筑工业出版社,1999:387-388.

Sun Jun.Rheologicalbehavior ofgeomaterials and its engineering applications[M].Beingjing:China Archtecture and Building Press, 1999:387-388.

[3] 何 峰,王来贵,赵 娜,等.煤岩蠕变破裂判定准则及应用[J].煤炭学报,2011,36(1):39-42.

He Feng,Wang Laigui,Zhao Na,etal.Criteria for coal creep rupture and itsapplication[J].Journal ofChina Coal Society,2011,36(1): 39-42.

[4] 薛凯喜,赵宝云,刘东燕,等.岩石非线性拉、压蠕变模型及其参数识别[J].煤炭学报,2011,36(9):1440-1445.

Xue Kaixi,Zhao Baoyun,Liu Dongyan,et al.Nonlinear creep model of rock in tensile or compressive stress and its parameter identification[J].Journal of China Coal Society,2011,36(9):1440-1445.

[5] 李亚丽,于怀昌,刘汉东.三轴压缩下粉砂质泥岩蠕变本构模型研究[J].岩土力学,2012,33(7):2035-2040.

Li Yali,Yu Huaichang,Liu Handong.Study of creep constitutivemodel of silty mudstone under triaxial compression[J].Rock and Soil Mechanics,2012,33(7):2035-2040.

[6] 王芝银,艾传志,唐明明.不同应力状态下岩石蠕变全过程[J].煤炭学报,2009,34(2):169-174.

Wang Zhiyin,Ai Chuanzhi,Tang Mingming.Complete process of rock creep in different stress states[J].Journal of China Coal Society,2009,34(2):169-174.

[7] 陈绍杰,郭惟嘉,程国强,等.深部条带煤柱蠕变支撑效应研究[J].采矿与安全工程学报,2012,29(1):48-53.

Chen Shaojie,Guo Weijia,Cheng Guoqiang,et al.Rearch on creep supporting effect of deep strip pillar[J].Journal of Mining&Safety Engineering,2012,29(1):48-53.

[8] 李栋伟,汪仁和,范菊红.软岩屈服面流变本构模型及围岩稳定性分析[J].煤炭学报,2010,35(10):1604-1608.

Li Dongwei,Wang Renhe,Fan Juhong.Yield surface constitutive creep model and stability analysis of soft rock roadway[J].Journalof China Coal Society,2010,35(10):1604-1608.

[9] 吴拥政.地应力异常区上山群巷道蠕变围岩控制技术[J].煤炭科学技术,2012,40(8):6-10.

Wu Yongzheng.Creep surrounding rock control technology of rise group roadway in abnormal ground stress zone[J].Coal Science and Technology,2012,40(8):6-10.

[10] Yang SQ,Jiang Y Z,Xu W Y,et al.Experimental investigation on strength and failure behavior of pre-cracked marble under conventional triaxial compression[J].International Journal of Solds and Structures,2008,45(17):4769-4819.

[11] 邢福东,朱珍德,刘汉龙,等.高围压高水压作用下脆性岩石强度变形特性试验研究[J].河海大学学报:自然科学版,2004, 32(2):184-187.

Xing Fudong,Zhu Zhende,Liu Hanlong,et al.Experimental study on strength and deformation characteristics of brittle rocks under high confining pressure and hydraulic pressure[J].Journal of Hohai University:Natural Science,2004,32(2):184-187.

[12] 吴秀仪,刘长武,沈荣喜,等.水压与外力共同作用下的岩石蠕变模型[J].西南交通大学学报,2007,42(6):720-725.

Wu Xiuyi,Liu Changwu,Shen Rongxi,et al.Creep model of rock subjected towater pressure and external force[J].Journal of Southwest Jiaotong University,2007,42(6):720-725.

[13] 赵宝云,刘东燕,郑志明,等.基于短时三轴蠕变试验的岩石非线性黏弹塑性蠕变模型研究[J].采矿与安全工程学报,2011, 28(3):446-451.

Zhao Baoyun,Liu Dongyan,Zheng Zhiming,et al.Non-linear viscoelastic plastic creep model of rocks based on the short time triaxial creep test[J].Journal of Mining&Safety Engineering,2011, 28(3):446-451.

[14] 朱杰兵,汪 斌,邬爱清.锦屏水电站绿砂岩三轴卸荷流变试验及非线性损伤蠕变本构模型研究[J].岩石力学与工程学报, 2010,29(3):528-534.

Zhu Jiebing,Wang Bin,Wu Aiqing.Study of unloading triaxial rheological tests and its nonlinear damage constitutive model of jingping hydropower station green sandstone[J].Chinese Journalof Rock Mechanics and Engineering,2010,29(3):528-534.

[15] 程先云.优化·拟合·建模:1stOpt应用详解[M].北京:中国建材工业出版社,2012:1-3.

Influence of high pore water pressure on creep properties of rock under high confining pressure

JIANG Hai-fei1,2,LIU Dong-yan1,HUANGWei1,LIU Fang-yu1

(1.College of Civil Engineering,Chongqing University,Chongqing 400045,China;2.State Key Laboratory of Coal Mine Disaster Dynamics and Control (Chongqing University),Chongqing 400044,China)

In order to study the influence ofwater pore pressure on time-dependent deformation of surrounding rock in the process of deep rock mass excavation under high stress,step loading triaxial creep test was carried out for deep sandstone from Chongqing under different pore water pressure.The results show that water pressure can enhance the performance of rock creep deformation,butwith the increase ofwater pressure,the deformation of rock is restrained in some extent at the initial loading phase.During rock creep,viscoelastic modulus changes exponentially with time.By analysing the variation of exponential expression parameter at differentwater pressure,expression of viscoelastic modulus varid with time and water pressure was obtained,then,a revisedmodified Kelvin was proposed which ismuch better to discribe the nonlinear viscoelastic creep characteristic in different water pressure.Based on the action of fine sandstone accelerating creep curvesat the level of differentwater pressure,a two component viscoplacticmodelwas acquired by themethod of fitting and anology,which is connected with the revised modified Kelvin model in series,then a new nonlinear viscoelastic-plastic constitutive model was gotten.According to test result,the optimize anglysis software1stOptwas choosed to identify themodel parameters,which hasa quite ideal effect.The testcurves are coincidentwellwith the theoretic cruves,which verified the correctness of themodel.

high confining pressure;high pore water pressure;fine sandstone;creep model

TD315

A

0253-9993(2014)07-1248-09

蒋海飞,刘东燕,黄 伟,等.高围压下高孔隙水压对岩石蠕变特性的影响[J].煤炭学报,2014,39(7):1248-1256.

10.13225/ j.cnki.jccs.2013.0918

Jiang Haifei,Liu Dongyan,HuangWei,etal.Influence of high pore water pressure on creep properties of rock under high confining pressure[J].Journal of China Coal Society,2014,39(7):1248-1256.doi:10.13225/j.cnki.jccs.2013.0918

2013-07-01 责任编辑:王婉洁

国家自然科学基金资助项目(41302223);交通部西部交通建设科技资助项目(2009318000001);中央高校基本科研业务费资助项目(CDJXS12200004)

蒋海飞(1982—),男,安徽肥东人,博士研究生。Tel:023-65123513,E-mail:13618207078@163.com