软火花电路的本安特性及优化分析

于月森,戚文艳,伍小杰

(1．中国矿业大学信息与电气工程学院,江苏徐州 221008;2．广东加华美认证有限公司上海分公司,上海 200030)

软火花电路的本安特性及优化分析

于月森1,戚文艳2,伍小杰1

(1．中国矿业大学信息与电气工程学院,江苏徐州 221008;2．广东加华美认证有限公司上海分公司,上海 200030)

提出一种可以有效提高本质安全型开关电源输出功率的电路结构——软火花电路,即在开关电源等效容性电路模型的末端添加附加电感,利用电感可延缓电流变化的作用减小短路火花电压与火花电流的重叠面积(即火花功率),进而提高本安电源输出功率。为了探究软火花电路的本安特性,首先通过数学推导得到在振荡和非振荡两种状态下火花电流和火花功率的数学表达式,并利用Mathcad仿真软件分析两种状态下电容量和电感量对短路火花功率的影响,结果表明附加电感在非振荡状态范围内取值对提高本安电源输出功率具有良好的效果;然后分析附加电感对原电路电气性能的影响,结果表明附加电感的存在对原电路的启动性能和负载动态响应性能没有显著影响,在可接受范围内;接着采用粒子群算法对软火花电路在多约束条件下的功率进行最优化分析,得到火花功率最优参数值;最后通过实验验证了分析结果的正确性。

本质安全特性;软火花电路;Mathcad仿真;粒子群算法

与线性电源相比,开关电源具有体积小、重量轻、电网适应性强、效率高、负载调整率好[1-3]的优点,在本安领域越来越得到广泛重视。本质安全电源的发展有从线性本安电源往开关型本质安全电源的趋势[4-8]。所谓本质安全,即在正常工作或规定的故障状态下产生的电火花或热效应均不会引燃规定的爆炸性气体混合物[9-10]。为了确保电源满足本质安全性能,常常需要采取一定的措施。文献[11]中提出一种基于输出本质安全要求的改进型Boost变换器,通过控制隔离开关的关断和主开关的导通,限制输出发生短路故障时的释放能量;文献[12]设计了一款截流型保护电路,当检测到故障时迅速关断开关管,减小故障处的火花释放能量;文献[13]分析研究了截流型容性电路的本安特性。以上措施均是通过附件开关器件限制输出火花释放能量实现防爆。在此基础上,为进一步提高本安开关电源的功率,需尽量减少火花电压和火花电流重叠部分以降低放电间隙处的火花释放能量。基于此本文利用电感电流不能突变,能有效的钳制电感电流维持初始状态,减少电流和电压交叠区域的特点,提出一种软火花技术—该技术通过在原电路末端添加附加电感而实现。本文在推导数学模型的基础上通过Mathcad仿真软件对振荡状态及非振荡状态下的软火花特性进行分析,得出火花功率随各参数的变化趋势;通过粒子群算法得到多约束条件下功率最优化求解,该方法有助于选取最小火花功率的参数值,在实际应用中具有指导作用;最后通过实验验证了分析结果的合理性。

1 软火花电路模型

软火花电路模型如图1所示。

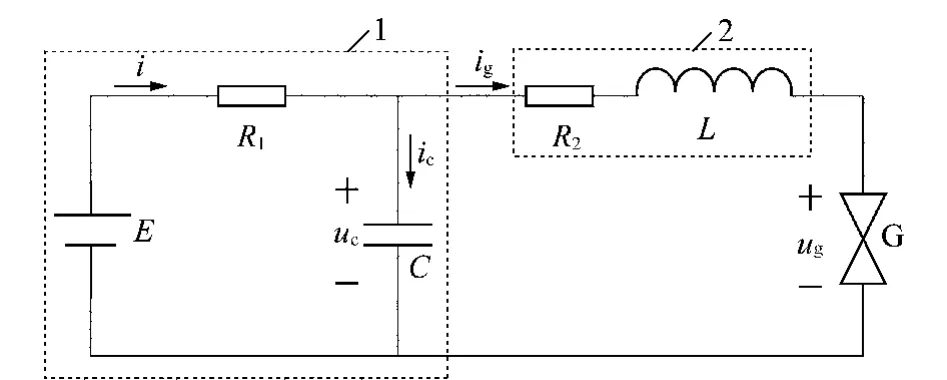
图1 软火花电路模型Fig．1 Model circuit of soft-spark

图中,1为开关电源的等效电路模型;E为电源电压;R1为电源内阻;C为电源等效输出电容;2为软火花的调整电路,由附加电感L和电阻R2构成,使原开关电源在火花试验装置中火花放电特性调整为软火花放电特性;G为IEC火花试验装置;ig,ic,i分别为放电期间总火花电流、电容放电电流及电源放电电流;uc为放电期间电容两端的电压;ug为火花放电电压。根据基尔霍夫定律对图1列写方程组

由式(2)可知,当B1＞(A1/2)2时,λ1,λ2取值为虚部为0的复数,电路处于振荡状态;当B1＜(A1/2)2时,λ1,λ2取值为实数,电路处于非振荡状态。振荡与非振荡的临界条件是B1=(A1/2)2,解得两个电感值,即

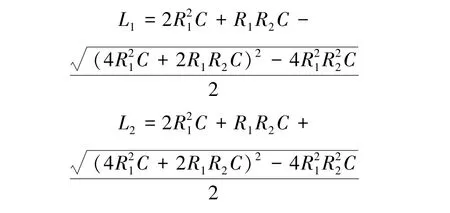
当附加电感满足L＞L2或0＜L＜L1时,电路处于非振荡状态;当L1＜L＜L2时,电路处于振荡状态。

电路在振荡状态下的火花瞬时电流及火花功率表达式分别为

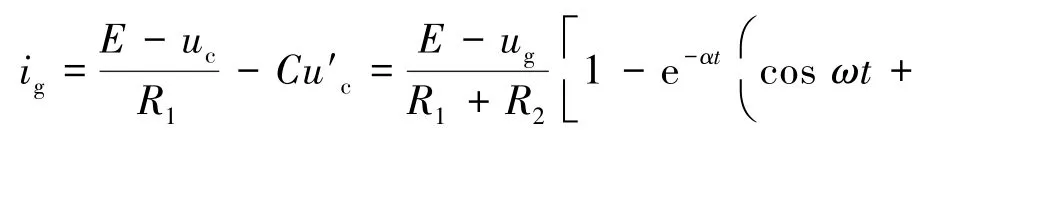
2 软火花电路的数值仿真分析

由于与火花放电特性相关的数学表达式非常复杂,从表达式不能直观地看出有意义的数据范围,也无法进行有效的比较。因而使用数学软件Mathcad进行数值仿真,分析上述数学模型中的参数关系。

2.1 电容对火花电流及功率的影响

2.1.1 振荡状态

当E=12 V,ug=10 V,R1=10 Ω,R2=1 Ω,L= 100 μH条件下,电容分别为10,30,50 μF时,不同电容值下火花瞬时电流和火花平均功率随时间的变化曲线,如图2所示。

图2 振荡状态下不同电容对火花电流及功率的影响Fig．2 The influence of spark current and power with different capacitance values in oscillation state

2.1.2 非振荡状态

当E=12 V,ug=10 V,R1=10 Ω,R2=1 Ω,L= 1 μH条件下,电容分别为10,30,50 μF时,不同电容值下火花瞬时电流和火花平均功率随时间的变化曲线,如图3所示。

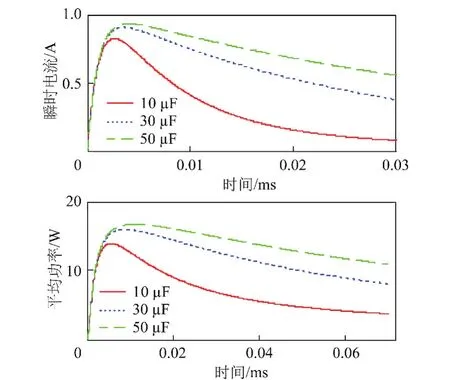
图3 非振荡状态下不同电容对火花电流及功率的影响Fig．3 The influence of spark current and power with capacitance values in non-oscillation state

由图2,3可以看出,无论是振荡情况还是非振荡情况下,随着电容值增大后,火花瞬时电流到达峰值的时间变长并且电流峰值随电容值的增大而增大,这些特性显示大电容更容易引发点燃。因此,电容虽然利于降低纹波等电气性能,但会影响电路的安全性能,不利于实现本质安全。

2.2 电感对火花电流及功率的影响

2.2.1 振荡状态

在E=12 V,ug=10 V,R1=10 Ω,R2=1 Ω,C= 10 μF条件下,电感分别为10,50,100 μH时,得到不同电感值下火花瞬时电流和火花平均功率随时间的变化曲线,如图4所示。

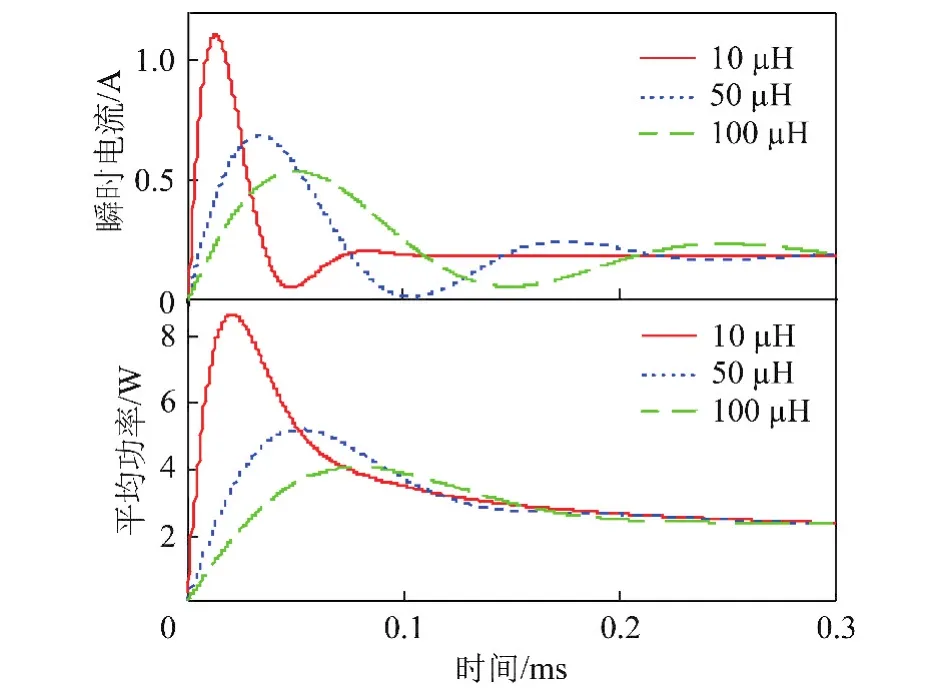
图4 振荡状态下不同电感对火花电流及功率的影响Fig．4 The influence of spark current and power with inductance values in oscillation state

由图4可以看出,在电路振荡条件下,随着电感值的增大,火花电流在上升阶段上升速度减慢,变化率降低,即电感的确起到延缓电流变化的作用。同时,火花电流达到峰值的时间变长,且电流峰值随电感量的增大而减小,火花功率逐渐减小。这说明调整电路确实达到了软火花的功能。从仿真数值上看,电感值在增大的同时,电路由振荡状态逐渐转向非振荡状态。对于此时的电路,电感处于L1＜L＜L2的范围内。

下面选取电感处于0＜L＜L1和L＞L2两种非振荡情况进行仿真研究。

2.2.2 非振荡状态

0＜L＜L1时,在E=12 V,ug=10 V,R1=10 Ω,R2= 1 Ω,C=10 μF条件下,电感分别为0．05,0．5,1 μH时,得到不同电感值下火花瞬时电流和火花平均功率随时间的变化曲线,如图5所示。

由图5可以看出,结论与图4相同：随着电感值的增大,火花电流达到峰值的时间变长,且电流峰值随电感量的增大而减小,火花功率逐渐减小。但是,在此种非振荡条件下,瞬时电流的最值比振荡情况下的最值增大很多,近似66%(以最小电感值为例)。

L＞L2时,在E=12 V,ug=10 V,R1=10 Ω,R2= 1 Ω,C=1 μF条件下,电感分别为500,700,1 000 μH时,得到不同电感值下火花瞬时电流和火花平均功率随时间的变化曲线,如图6所示。

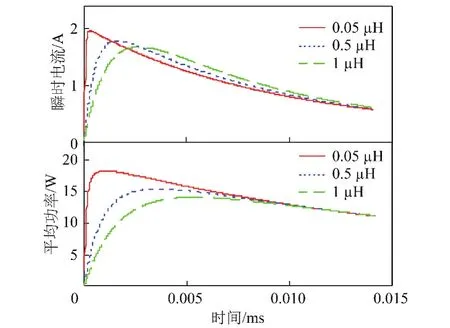
图5 非振荡状态下不同电感对火花电流及功率的影响(0＜L＜L1)Fig．5 The influence of spark current and power with inductance values in non-oscillation state(0＜L＜L1)

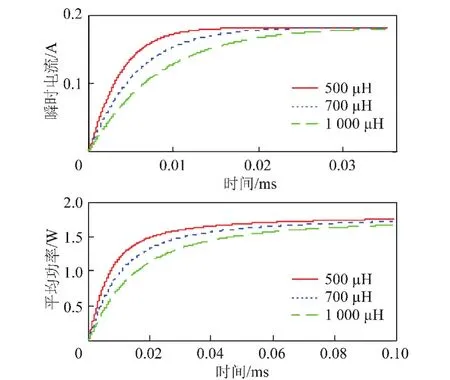
图6 非振荡状态下不同电感对火花电流及功率的影响(L＞L2)Fig．6 The influence of spark current and power with inductance values in non-oscillation state(L＞L2)

由图6可以看出,此时的电流和功率曲线数值均非常小,瞬时电流的稳定值稳定在0．18 A左右,平均功率的稳定值约为1．7 W。此时,延缓电流变化的作用很明显,但电感值非常大,在开路情况下受电感影响,电路也会出现开路火花,造成一定的危险性。

为进一步理解电感对原电路的影响,将不同电感下电路的火花电流及功率进行比较(图7),各参数取值为E=12 V,ug=10 V,R1=10 Ω,R2=1 Ω,C= 10 μF,电感为0时,电路为电容等效电路;电感为2 μH和4 500 μH时,电路为非振荡状态;电感为10 μH和100 μH时,电路为振荡状态。

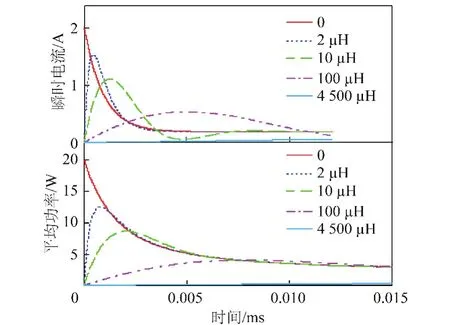
图7 不同电感对火花电流及功率的影响Fig．7 The influence of spark current and power with different inductance values

由仿真图可看出L＜L1条件下非振荡状态,添加电感值很小,电流和功率改变也比较微弱。L＞L2条件下非振荡状态,电流和功率峰值降低了75%,但此时的电感值非常大,会造成开路火花,所以非振荡状态不适用于软火花电路。根据上述分析,振荡状态下电感值不大,其效果很显著,是非常适合的选择范围。

由以上分析可知,L1＜L＜L2是提高本安电源输出功率的最佳取值范围。

2.3 附加电感对电气性能的影响

下面进一步分析附加电感的引入对原电源电气性能的影响,经查阅简单电感电路的临界点燃曲线可知,当E=12 V,I=1．2 A时对应的临界电感值为800 μH,且电流越大时临界值越小。因此,为满足本安性能,电感的最大取值为800 μH,即当L2＜800 μH时,电感的范围为L1＜L＜L2,当L2＞800 μH时,电感的范围为L1＜L＜800 μH。论文选取最恶劣情况,即L1＜L＜800 μH的电感范围,对电源电气性能的影响进行研究。

2.3.1 启动性能

为了研究电感对电源启动性能的影响,利用Saber中的可编辑器件v-pwl,将电源输出电压特性设置为如图8所示的曲线,不同软火花电感对输出特性的影响如图9所示。

图8 电源输出电压特性曲线Fig．8 Power supply output voltage characteristic

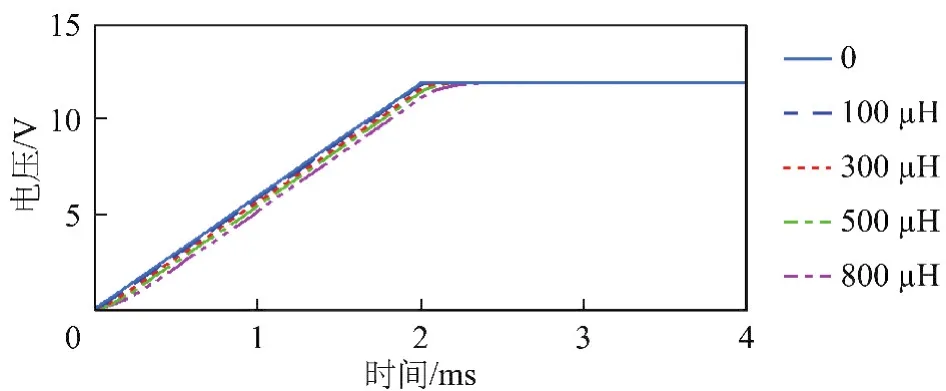
图9 不同电感下的电源输出电压波形Fig．9 Power supply output voltage curves in different inductance values

由图9可以看出,随着电感值的增大,电源启动调整时间有所变长,当取电感最大值L=800 μH时,启动调整时间最长,约为2．2 ms,但该数值与原有启动时间相比,差别不大,即软火花电感对于启动时间没有明显的影响。

2.3.2 负载动态响应性能

为了研究软火花电感对电源负载动态响应的影响,利用Saber中的可编辑器件pwlr,将负载电阻设置为如图10所示的曲线。此时电源的输出电压波形如图11所示。

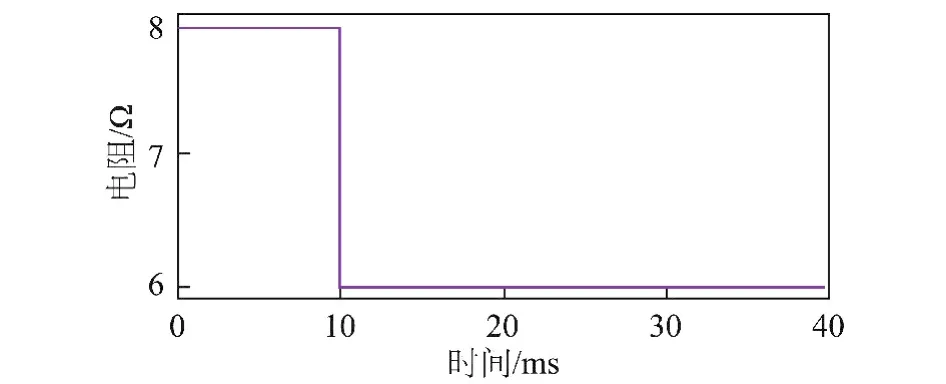
图10 负载突变曲线Fig．10 Load suddenly changing curve

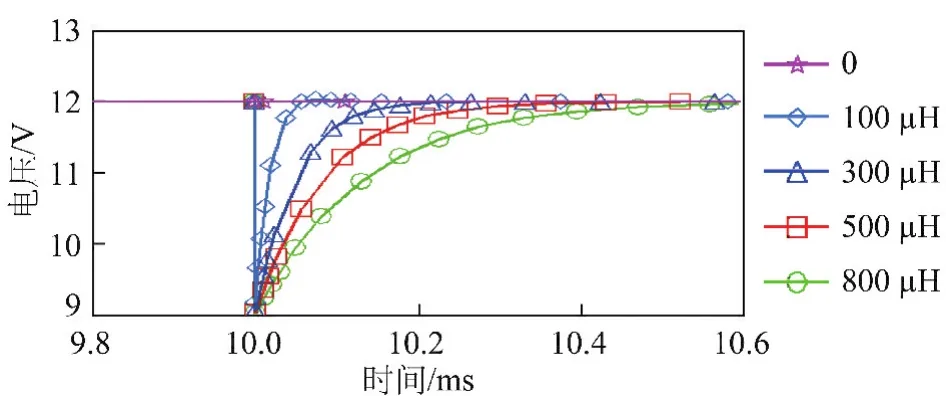
图11 不同电感下的电源输出电压波形Fig．11 Output voltage curves in different inductance values

由图11可以看出,随着电感值的增大,输出电压调整时间逐渐增大,当取最大值L=800 μH时,调整时间最长,约为0．5 ms,调整较快。

通过以上分析可知,在软火花电感最大取值范围内,即L1＜L＜800 μH时,附加电感不影响电源的电气性能指标。

3 软火花电路的优化分析

通过Mathcad仿真软件知功率与各个参数间的变化趋势。为进一步探究软火花提高功率的能力,进行优化分析。粒子群算法可以实现多目标最优求解,算法规则简单、容易实现、工程应用比较广泛,并且收敛速度快,参数选择比较成熟[14-15],由于以上种种优点,所以采用粒子群算法对软火花电路进行优化分析。

本文优化分析可描述为：在电路系统一部分参数确定下,关键参数(电容、电感、放电时间)以最小火花平均功率为目标,确定各个参数的最优组合。具体的数学模型描述为

电路存在振荡和非振荡两种不同的工作模式,振荡模式下,输出功率为式(4);非振荡模式下则为式(6)。

电路的其他参数为E=12 V,ug=10 V,R1= 10 Ω,R2=1 Ω。

由图12可以看出,火花功率在逐渐降低,经过100次的迭代,功率最值趋于稳定,则可认为是粒子群算法的最终优化结果。

经过多次运算,选择电容值为10 μF左右,火花放电时间为100 ms左右的5组最优化结果绘制出图13,可以看出经过多次的优化选择,在电感为488 μH,得到最优化的功率值为1．636 9 W。

通过粒子群算法,得到多约束条件下的最优化求解。此方法帮助选取最小火花功率的参数值,在实际应用中具有指导作用。

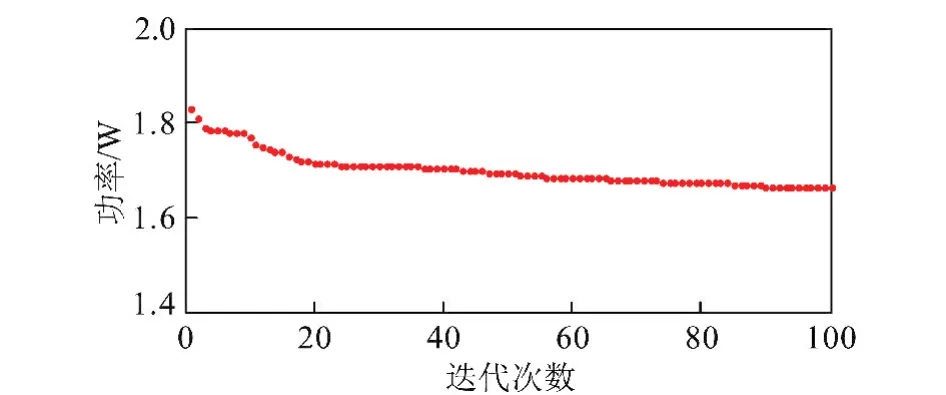
图12 迭代次数与功率的关系Fig．12 The relationship between spark power and iterations frequency

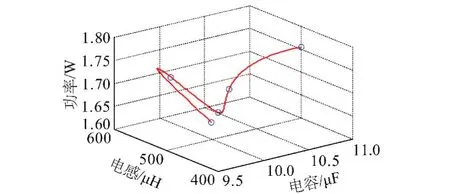
图13 功率优化曲线Fig．13 Optimal power curve

4 软火花电路实验验证

为便于实验观察振荡与非振荡状态,选取参数如下：电源电压E为12 V,电容C为10 μF,电阻R1为50 Ω,电阻R2为10 Ω。

电感L为10 μH时,火花电压、电流及功率实验波形如图14(a)所示;电感L为100 μH时,火花电压、电流及功率实验波形如图14(b)所示。在这两种情况下,电路处于非振荡状态。电感L为220 μH时,火花电压、电流及功率实验波形如图14(c)所示,此时电路为临界振荡状态。

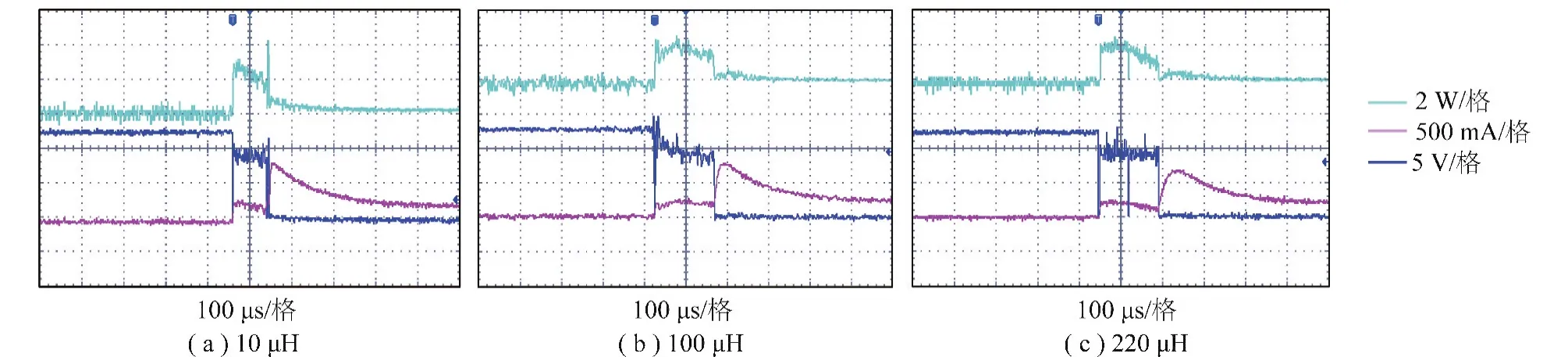
图14 非振荡火花放电电压、电流及功率实验波形(L=10 μH)Fig．14 Spark voltage,current and power waveforms in non-oscillation state(L=10 μH)

从图14可以看出,在非振荡状态下,电路的火花电流及火花功率随着电感值的增大逐渐减小,但是效果不是很显著。

电感L=320 μH时,火花电压、电流及功率实验波形如图15(a)所示;电感L=540 μH时,火花电压、电流及功率实验波形如图15(b)所示这两种情况下,电路处于都振荡状态。

由上述振荡状态电路所示,在振荡状态下,随着电感值的增大,电路的火花电流及火花功率迅速减小,说明调整电路确实可以达到降低火花电流及火花功率的目标,即软火花技术可以提高本质安全电源功率。

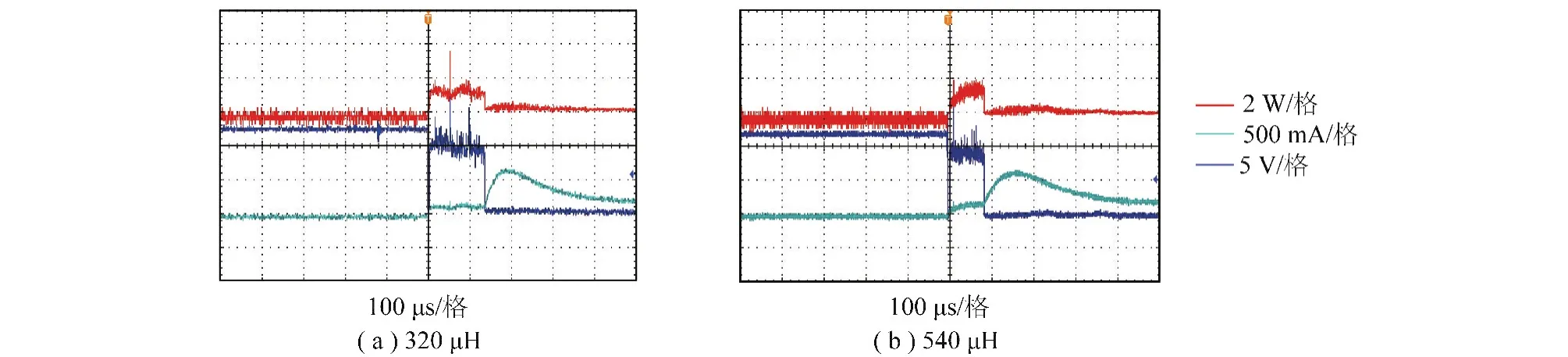
图15 振荡火花放电电压、电流及功率实验波形Fig．15 Spark voltage,current and power waveforms in oscillation circumstance

5 结 论

(1)软火花电路存在振荡与非振荡两种状态;两种状态下随着电感值的增大,电感峰值电流及火花功率均随之减小,电感起到延缓电流变化的作用;但振荡状态下的电参数更适合实现软火花电路。

(2)通过粒子群算法可以实现最小火花功率的最优设计参数值。

(3)适当选取附件电感,可使软火花电路显著减小火花电流及火花功率,从而有效提高本安电源功率,且对于原电路的电气性能影响不大。

[1] 蔡宣三,张占松．开关电源的原理与设计[M]．北京：电子工业出版社,2004．

[2] 崔保春,王 聪,卢其威,等．矿用本质安全开关电源的研究[J]．中国煤炭,2006,32(3)：47-49．

Cui Baochun,Wang Cong,Lu Qiwei,et al．Study of mine intrinsic safety switching power supply[J]．China Coal,2006,32(3)：47-49．

[3] 张玉良．一种带备用电池多路输出的隔爆兼本质安全型开关直流稳压电源[J]．煤矿自动化,1996(4)：57-59．

Zhang Yuliang．A multiplexed output explosion-proof and intrinsically safe dc regulated switching power supply with reserved battery [J]．Coal Mine Automation,1996(4)：57-59．

[4] Huczko．Intrinsically safe power source[P]．United States Patent： 5694283,2004-11-25．

[5] Claude ercier．Intrinsically safe universal switching power supply [P]．United States Patent：6590788 B2,2003-07-08．

[6] 刘树林,刘 健,寇 蕾．开关变换器的本质安全特性分析与设计[J]．电工技术学报,2006,21(5)：36-41．

Liu Shulin,Liu Jian,Kou Lei．Intrinsically safe behavior of switching converters and its design[J]．Transactions of China Electrotechnical Society,2006,21(5)：36-41．

[7] 于月森,谢冬莹,李世光,等．本质安全电路技术综述[J]．煤炭科学技术,2011,39(6)：61-65．

Yu Yuesen,Xie Dongying,Li Shiguang,et al．Summary of intrinsic safety electric circuit technology[J]．Coal Science and Technology, 2011,39(6)：61-65．

[8] 崔保春,王 聪．本质安全电源电路理论综述[J]．电源世界, 2006(12)：1-6．

Cui Baochun,Wang Cong．The theoretical survey of intrinsically safe supply circuits[J]．The World of Power Supply,2006(12)：1-6．

[9] GB 3846．4—2010．中国强制性国家标准汇编：电工卷[S]．

[10] Adams J M．Electrical apparatus for flammable atmosphere[J]．Power Engineering Journal,1990(6)：278-282．

[11] 刘树林,焦水林,刘 健,等．输出本质安全型Boost变换器的改进电路研究[J]．煤矿机电,2005(5)：67-69．

Liu Shulin,Jiao Shuilin,Liu Jian,et al．A study of improved circuit for boost converter based on output intrinsic safety[J]．Colliery Mechanical and Electrical Technology,2005(5)：67-69．

[12] 于月森．本质安全型开关电源基础理论与应用研究[D]．徐州：中国矿业大学,2012．

Yu Yuesen．Study on the theory and application of the intrinsically safe switch power supply[D]．Xuzhou：China University of Mining and Technology,2012．

[13] 于月森,张 望,孟庆海,等．截止型保护方式下容性电路短路火花放电模型及分析[J]．煤炭学报,2013,38(3)：517-521．

Yu Yuesen,Zhang Wang,Meng Qinghai,et al．Modeling and analysis on spark discharge of capacitive circuit with cut-off type protection[J]．Journal of China Coal Society,2013,38(3)：517-521．

[14] 于 颖,李永生,於孝春．粒子群算法在工程优化设计中的应用[J]．机械工程学报,2008,21(12)：226-231．

Yu Ying,Li Yongsheng,Yu Xiaochun．Application of particle swarm optimization in the engineering optimization design[J]．Journal of Mechanical Engineering,2008,21(12)：226-231．

[15] 刘 佳,李 丹,高立群,等．多目标无功优化的向量评价自适应粒子群算法[J]．中国电机工程学报,2008,28(31)：22-28．

Liu Jia,Li Dan,Gao Liqun,et al．Vector evaluated adaptive particle swarm optimization algorithm for multi-objective reactive power optimizatio[J]．Proceedings of the CSEE,2008,28(31)：22-28．

Intrinsically safe characteristics and optimization analysis of soft-spark circuit

YU Yue-sen1,QI Wen-yan2,WU Xiao-jie1

(1.School of Information and Electrical Engineering,China University of Mining and Technology,Xuzhou 221008,China;2.Shanghai Branch,CCIC-CSA International Certification Co.,Ltd.,Shanghai 200030,China)

In order to improve the output power of switching power supply,a soft-spark circuit is proposed in which an appended inductor is laid at the end of the equivalent capacitive circuit model of switching power supply．As the inductor can delay current variation,the overlap area of spark voltage and spark current(namely the spark power)can be effectively reduced so as to improve the output power of intrinsically safe switching power supply．To investigate the intrinsically safety performance of the soft-spark circuit,firstly,the spark current and spark power in the circumstances of oscillation and non-oscillation are respectively deduced through mathematical deduction,and the Mathcad simulation software is used to simulate the effect of capacitance and inductance on spark power,which indicates the inductance values in non-oscillation circumstance have effectively improved the output power．Secondly,the influence of the appended inductance on the electrical performance of primary circuit is analyzed,which indicates the inductance has no obvious impact on starting performance and load dynamic response performance,which is in an allowed range．Thirdly, the particle swarm algorithm is applied to analyze the power of the soft-spark circuit under more constraint so as to obtain power optimization value．Finally,the experiments are conducted to verify the results．

intrinsically safe performance;soft-spark circuit;Mathcad simulation;particle swarm algorithm

TD684

A

0253-9993(2014)10-2134-07

2013-10-03 责任编辑：许书阁

国家自然科学基金资助项目(51304191);中央高校基本科研业务费专项资金资助项目(2012ONB30)

于月森(1978—),男,山东五莲人,副教授。E-mail：yuyuesen@cumt．edu．cn

于月森,戚文艳,伍小杰．软火花电路的本安特性及优化分析[J]．煤炭学报,2014,39(10)：2134-2140．

10．13225/j．cnki．jccs．2013．0732

Yu Yuesen,Qi Wenyan,Wu Xiaojie．Intrinsically safe characteristics and optimization analysis of soft-spark circuit[J]．Journal of China Coal Society,2014,39(10)：2134-2140．doi：10．13225/j．cnki．jccs．2013．0732