基于模块化多电平换流器的新型高压变频器拓扑及其控制

郑 征,崔 灿,张 朋

(河南理工大学电气工程与自动化学院,河南焦作 454000)

基于模块化多电平换流器的新型高压变频器拓扑及其控制

郑 征,崔 灿,张 朋

(河南理工大学电气工程与自动化学院,河南焦作 454000)

为使煤矿设备高效利用能源,达到节能减排的目的,提出了基于模块化多电平换流器(Modular Multilevel Converter,MMC)的新型高压变频器。概述了其基本结构,分析了MMC拓扑及工作机制。以逆变侧为研究对象,建立MMC数学模型,采用建模排序法控制子模块电容电压稳定平衡,通过与不同调制算法对比,载波正负反相层叠脉冲宽度调制技术(POD-PWM)的优势得以凸显。以Matlab-Simulink及RT-Lab半实物仿真设备为实验平台,搭建上位机控制器,实验结果显示换流器运行正常、电容电压稳定平衡,输出电能质量高,谐波含量小,证明了提出的载波正负反相层叠与电压稳定平衡控制相结合的控制策略的可行性,并得出了实验条件下的最佳三角载波频率。

高压变频器;模块化多电平换流器;调制算法;建模排序法电压稳定平衡控制;RT-Lab

随着工业发展,能源矛盾日益突出,节能减排已成为我国基本国策。煤矿企业既是产能大户,也是耗能大户,矿用大型动力设备主要包括提升机、运输机、风机、水泵等高压大功率装置。目前,传统电压源型交-直-交高压变频器,其拓扑无论是二极管箝位型结构、飞跨电容型结构、H级联桥串联结构等,大都无法实现四象限运行,这种变频器不能直接用于像矿用提升机等需要快速启动、制动,频繁正反转的调速系统,且制动能量无法直接回馈给电网,不能达到节能的效果;同时还存在网侧电流波形畸变严重,含有大量的低次谐波,形成电力公害等问题[1-6],一定程度上造成了煤矿生产成本的升高。

近些年,模块化多电平变换器(modular multilevel converter,MMC)受到广泛关注[7],它继承了H桥级联结构的优势,通过功率单元的级联实现多电平输出。每个功率单元由一个两电平桥臂构成,且所有的电容处于悬浮状态,由于存在公共直流母线,可采用单一直流电压而不需要多绕组变压器[8],该换流器产生谐波少、开关损耗与畸变率低,在高压直流输电方向,已有2项工程投入运行,分别是西门子公司承建的美国旧金山市Trans Bay Cable和我国电力科学研究院在上海建立的南汇风电场柔性直流输电工程[9];本文将此新型变换器应用于煤矿设备,可以达到节能减排、高效利用能源的目的。

本文简述了高压变频器拓扑结构,基于MMC的高压变频器,整流侧、逆变侧采用完全相同的拓扑结构,因此工作机制相同。本文以逆变侧为分析对象,建立换流器的开关函数模型,通过对各个子模块电容电压检测、排序、充放电来实现电容电压平衡控制,同时采用建模法控制电容电压的稳定,并对比不同调制技术优劣。最后在Matlab-Simulink及RT-Lab环境下建立模型进行仿真验证。

1 高压变频器拓扑结构

该新型高压变频器,如图1所示,变频器在输入端,通过基于MMC多电平整流模块直接级联的方式取消了传统的移相式高压变频器的工频变压器,由于存在公共直流母线,通过对直流母线电压的控制实现输入输出功率的变换。与H桥级联式多电平变换器相比,大大简化了电路结构,且使得故障检测及控制变得简单;其次,该高压变频器网侧和负载侧形成背靠背的对称结构,均采用全控器件组成,因此,该变频器通过逆变侧为电机提供高质量三相交流电源同时,还能将再生电能通过整流测回馈电网。最后,由于MMC允许使用标准化元件,可以在采用相同器件的前提下向不同的功率和电压等级扩展,因此无需使用变压器就可以应用在矿用动力设备、高压直流输电、牵引供电等中高压大功率场合。由此可见,基于MMC的高压变频器可以克服传统的高压变频器所存在的问题,且其结构应用前景广泛。

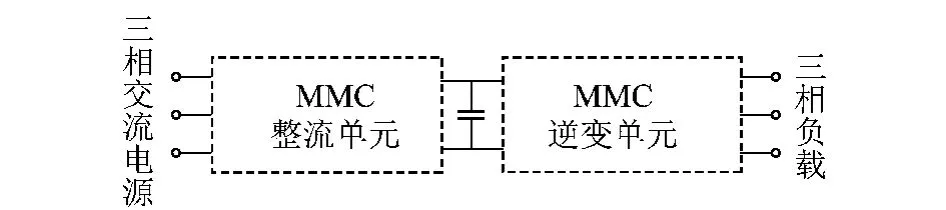
图1 基于MMC的变频器拓扑结构Fig．1 Topological structure for frequency converter based on MMC

2 MMC拓扑结构及其工作机制

MMC拓扑结构如图2所示,换流装置由A,B,C三相组成,每一相分为上、下两个桥臂,每个桥臂由N个完全相同的子模块(Sub-Modular,SM)级联而成。每个桥臂子模块可以进行有选择的控制,从而可将其等效为一个可控理想电压源,作为逆变器使用时,通过控制每个桥臂子模块导通状态,就可以在输出端得到所需的正弦电压。该换流器结构简单,能够实现四象限运行,弥补了传统换流装置的一些不足,输出电能质量高。

换流器正常运行时,任意时刻,每一相投入的子模块总数为N,这样既可产生具有N+1种电平的阶梯波。随着子模块数目增加,多电平叠加产生的阶梯波可逐渐逼近正弦波形式。电平数增加,主电路结构也随之改变,需增加开关管,但增多的仅是低压低频开关器件,减少开关损耗同时,利用低压器件进行分压,实现高压大功率电能变换。

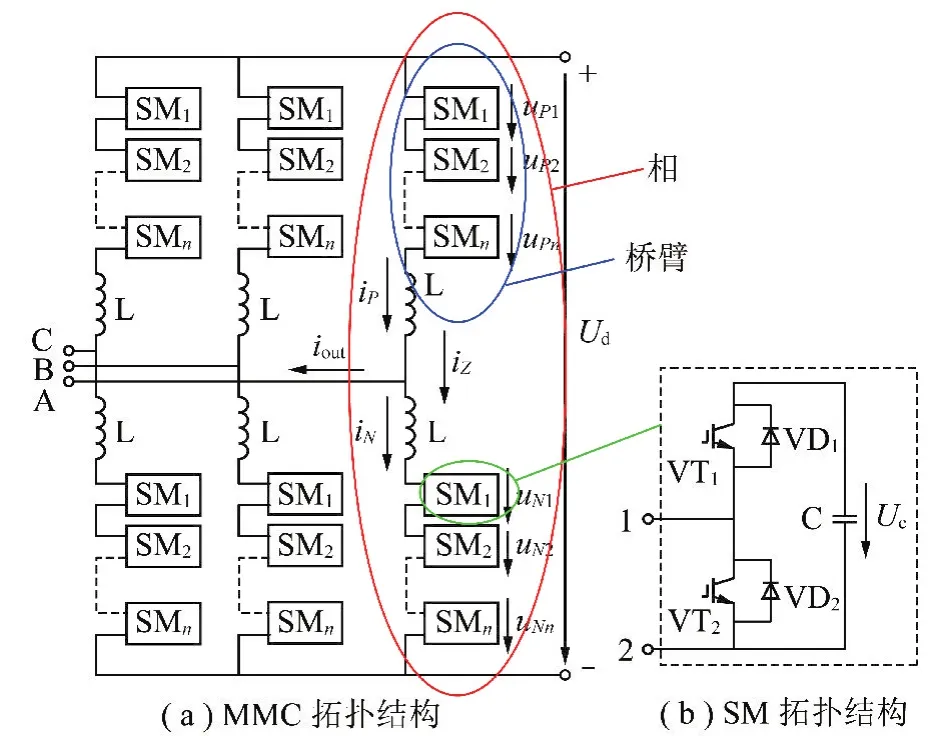
图2 MMC拓扑结构Fig．2 Structural diagram of MMC topology

子模块可分为上、下两个桥臂,共有6种工作模式,可分为闭锁、切出、投入3种工作状态,当系统出现故障时,子模块两个IGBT全部被关断,处于闭锁状态,正常工作时每个子模块都处于投入或者切出状态,如图3所示。

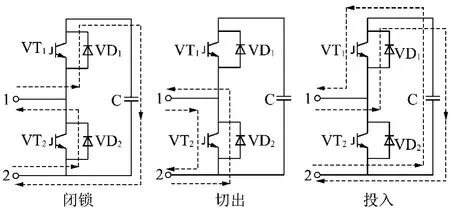
图3 SM工作状态Fig．3 Working states for SM

3 建模法MMC电容电压稳定控制

MMC系统采用相同子模块级联而成,所以三相运行状态完全相同,本文分析皆以图4中A相7电平为例。子模块电容电压平衡、稳定是MMC系统正常运行前提,本文采用排序法控制电容电压平衡[10],限于篇幅此处不再赘述。以此为基础[11-14],下面进行建模法电压稳定控制的详细分析。

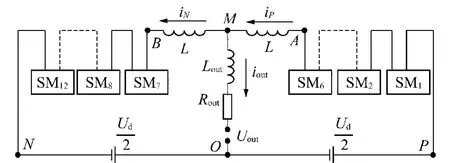
图4 A相电路结构Fig．4 Circuit structure for A phase

当系统的子模块投入运行时,子模块的输出电压为并联电容的电压值UC;切出时,子模块输出电压为0,由此可将桥臂子模块的数学模型用开关函数S[15]来表达,即

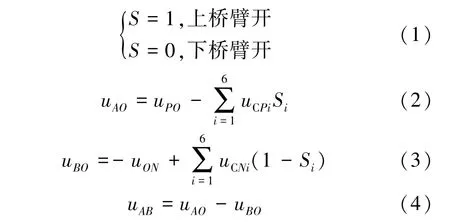
式中,uCPi,uCNi为上、下桥臂第i个子模块电容电压。

不接负载时,设M和O点之间的电压为uth。则

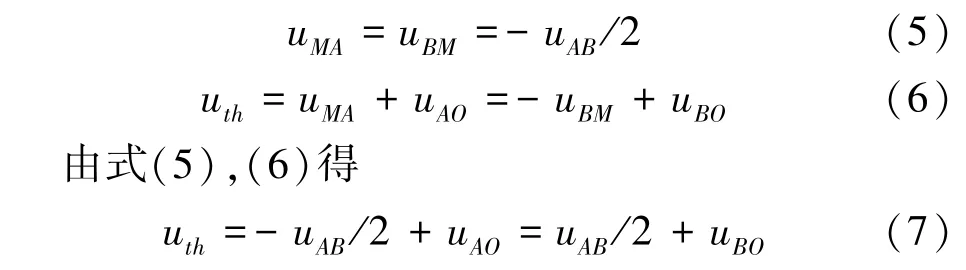
将图4所示电路等效简化,结构如图5所示。

图5中,Lth=L//L=L/2,由基尔霍夫电压定律得

图5 A相简化电路结构Fig．5 Simplified structure for A phase

根据以上推导的数学公式,建立准确的数学模型,即可得控制子模块电容电压稳定的框图(图6)。

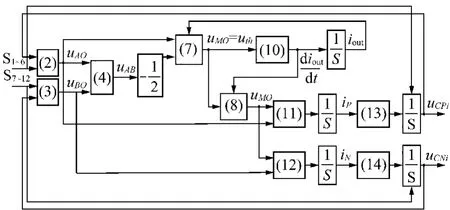
图6 SM电容电压稳定控制流程Fig．6 Control flow chart for SM capacitor voltage

4 调制算法对比分析

目前MMC调制策略主要有阶梯波脉宽调制技术、消除特定次谐波调制、移相多载波调制技术、开关频率最优化,空间矢量PWM等,上述调制方法均有可能因开关频率过高而带来较大的损耗,使功率器件的开关频率潜能得不到充分发挥,尤其在多电平高压变换电路中,该问题尤为严重,载波层叠调制技术,在消除电压谐波方面具有一定优势,同时通过提高等效开关频率、减小系统损耗。目前,载波层叠调制分为：同相层叠(PD-PWM)、正负反向层叠(POD-PWM)、交替反向层叠(APOD-PWM),如图7所示。

理论上任何时变波形都可以用式(11)所示的无限序列正弦波分量表示,其中第k次谐波分量的幅值Ck由傅里叶积分表示为式(12),利用双重傅里叶变换得到谐波的统一表达式(13),式中第1项为直流分量,第2项为基波,第3项为载波谐波,第4项为载波边带谐波。

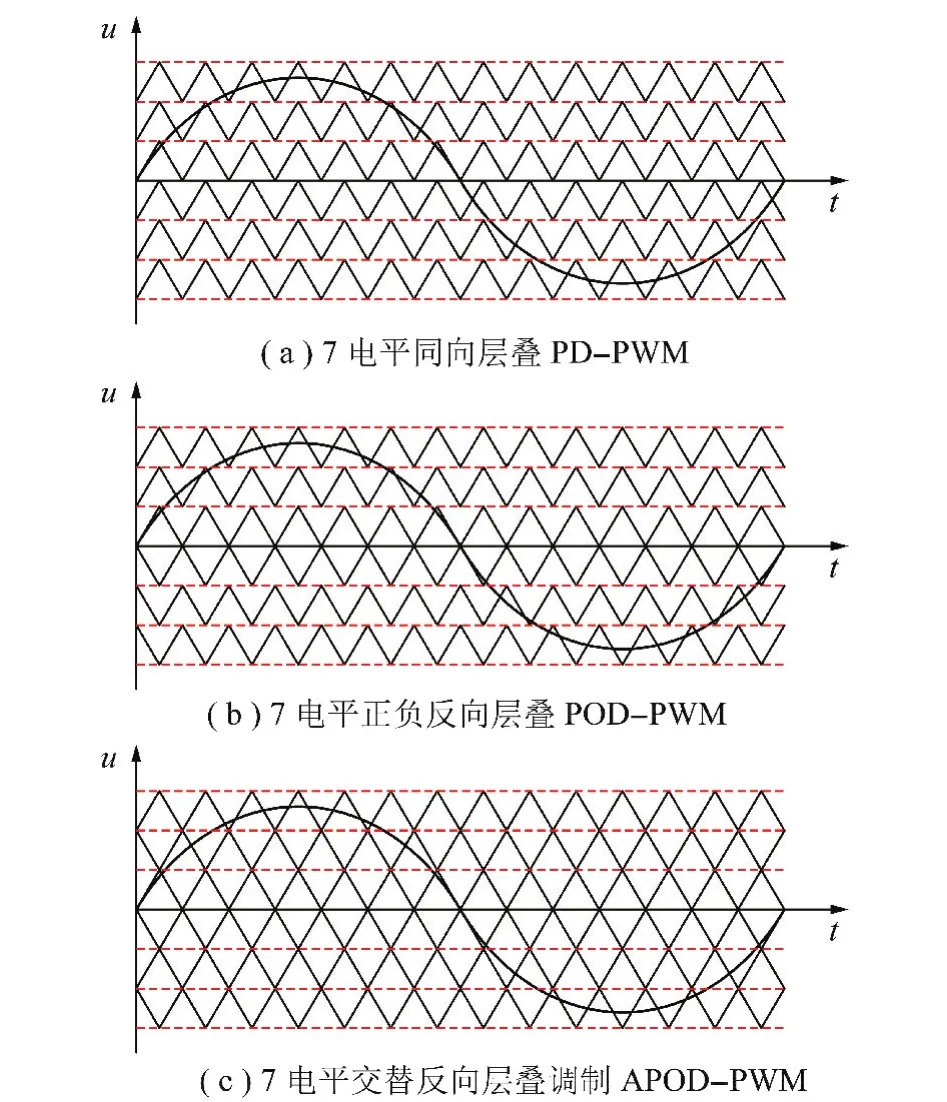
图7 载波层叠调制技术分类Fig．7 Classification for carrier wave disposition modulation

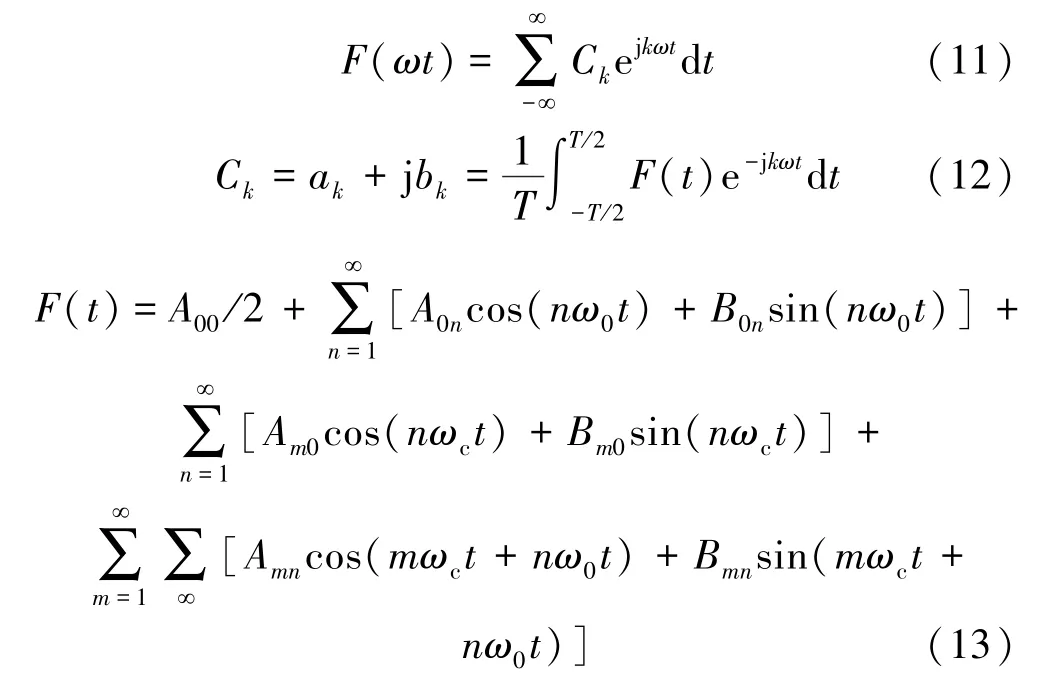
经过适当数学变换,多电平多载波PWM控制法所得到的输出电压表达式都可由式(13)中的部分或全部谐波分量组成,因此从理论上可以得到任何多电平多载波PWM法的准确式子,但实际推导过程十分复杂,很难得出相应表达式,所以在研究多电平多载波调制方法中寻找最佳载波频率时,以理论为基础,通过仿真实验来得到相应结果是较好的一个方式[16]。

经实验研究,从消除谐波程度来看,POD-PWM的性能最好,PD-PWM次之,APOD-PWM效果最差。在Matlab-Simulink仿真环境下搭建三相七电平MMC逆变器模型,进行仿真验证,模型参数见表1。

仿真结果如表2、图8所示,在相同条件下,对比数据,POD-PWM法输出效果最佳,总谐波畸变率低,仅含有少量高次谐波,尤其是相电压谐波含量最少。

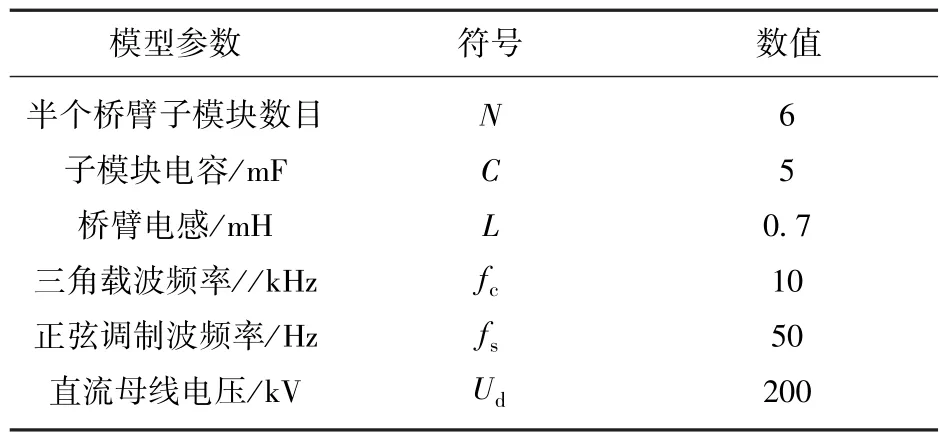
表1 MMC仿真参数Table 1 Parameters of modulation for MMC

表2 3种调制方法输出电压、电流的THDTable 2 The THD data of output voltage and current for three different modulations%

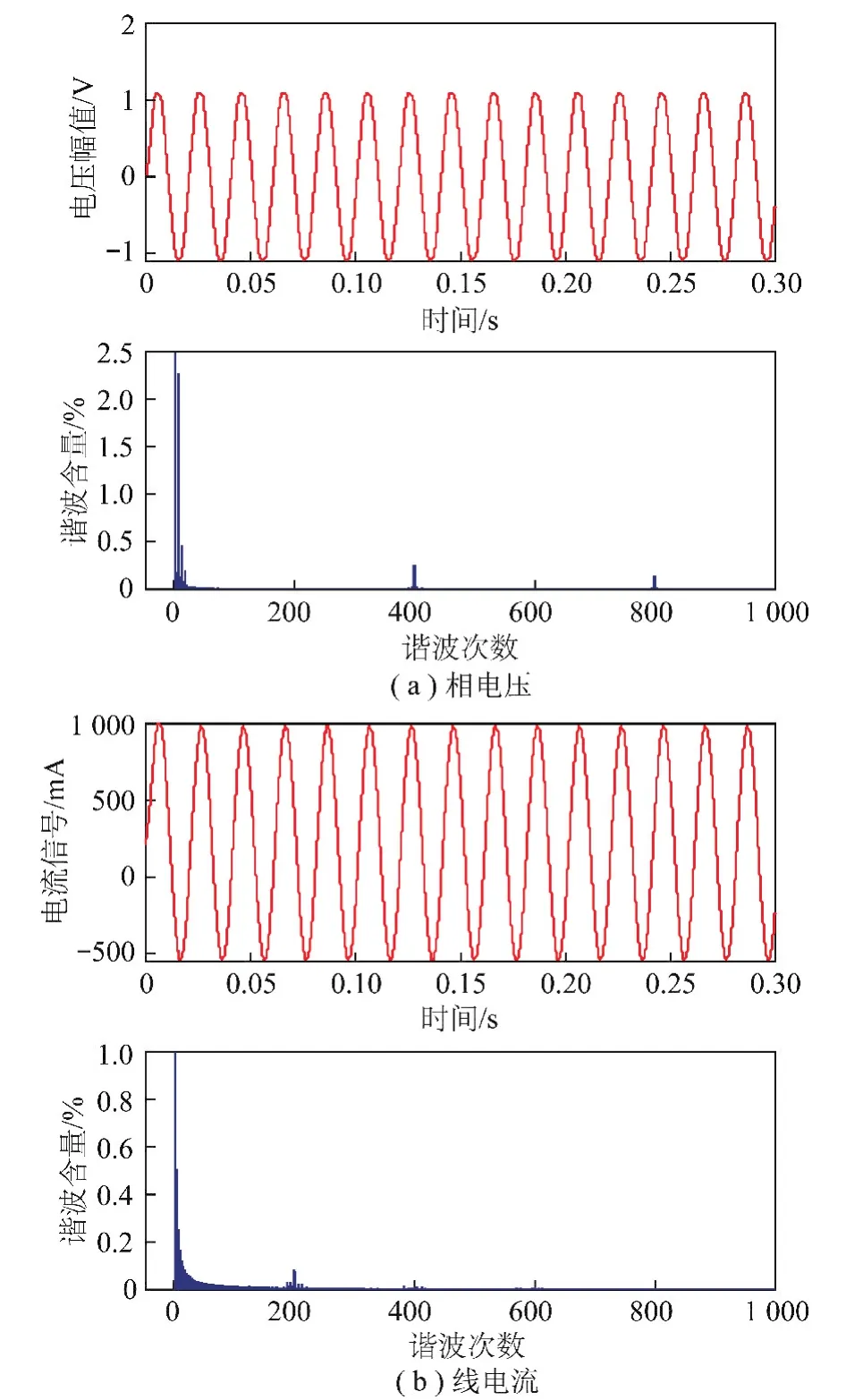
图8 POD-PWM法输出电压、电流波形分析Fig．8 The output voltage and current analysis for POD-PWM

图9为子模块电容电压从启动到稳定的动态过程波形。换流器正常运行时,子模块电容电压在33．35 kV左右浮动,与理论计算值33．33 kV十分接近。仿真步长为50 μs,所以从启动到子模块电容电压稳定,只需60 ms左右,快速性突出。

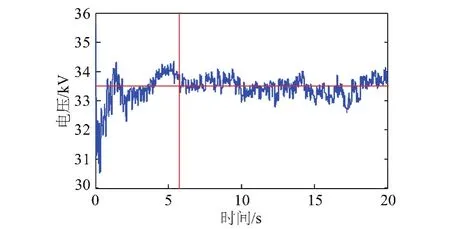
图9 SM电容电压启动波形Fig．9 Waveform for SM capacitor starting voltage

图10是换流器正常运行时子模块电容电压波形,由图可知稳定性良好。根据前面结论可知,从数学分析来看很难得出具体表达式,因此这里采用实验验证的方法针对POD-PWM做进一步深入分析,研究在一定条件下采用频率为多少的三角载波,可使输出电压谐波含量最少。设调制度为0．975,正弦调制波为工频50 Hz,仿真结果见表3,可知当三角载波频率为8 017 Hz左右时,输出相电压、线电流的THD最低。

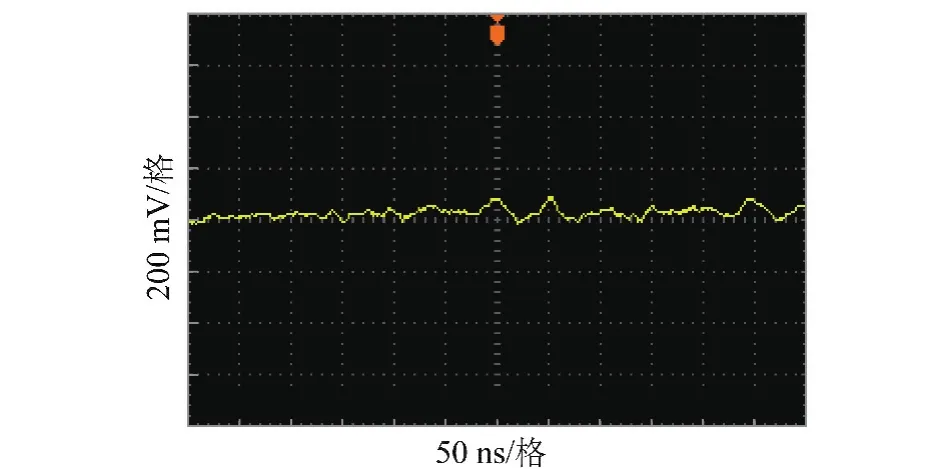
图10 SM电容电压稳定波形Fig．10 Stable waveform for SM capacitor voltage

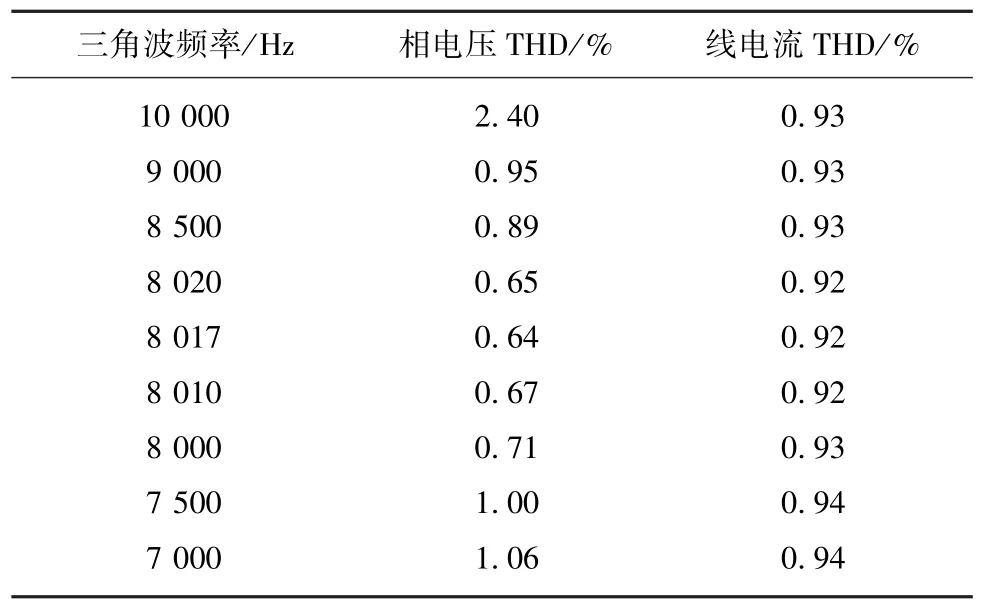
表3 载波频率与输出电压、电流的THDTable 3 Relationship between the carrier wave frequency and the THD for output wave

5 RT-Lab实验

RT-Lab半实物仿真平台,是由加拿大Opal-RT Technologies公司推出的一套工业级的系统设备,如图11所示,通过RT-Lab,工程师可以直接将利用Matlab-Simulink环境下建立的动态系统数学模型应用于实时仿真、控制、测试以及其他相关领域,是一种全新的基于模型的工程设计应用平台。工程师可以在一个平台上实现工程项目的设计,实时仿真,快速原型与硬件在回路测试的全套解决方案,可以在最短时间内、用最少花费达到验证工程的目的。以其作为上位机进行控制,配合实验室现有的自主开发制作的MMC逆变器设备作为被控对象,可以实现多种算法开发研究。

图11 RT-Lab半实物仿真平台Fig．11 RT-Lab hardware in loop simulation

MMC逆变器的实际实验设备参数设置见表4,结合经实验测试得出的最佳三角载波频率,采用POD-PWM法,在RT-Lab中搭建三相七电平MMC逆变器的控制器,作为上位机对目标设备MMC逆变电路进行控制。

表4 MMC逆变器参数Table 4 Parameters for MMC inverter

图12为输出相电压阶梯波,经过相应比例缩减,用示波器测得逆变器实际输出相电压峰值在10 V左右。滤波处理后,输出电压如图13上部所示,十分接近正弦波,下部为输出相电压中谐波分布情况,由图中曲线可知,变换器输出电压谐波含量较少,电能质量高。

6 结 语

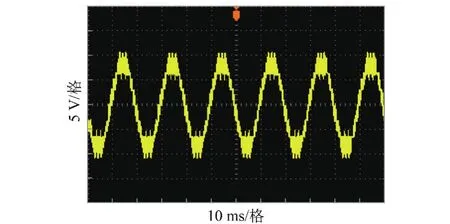
图12 输出相电压阶梯波Fig．12 The output step waveform for phase voltage

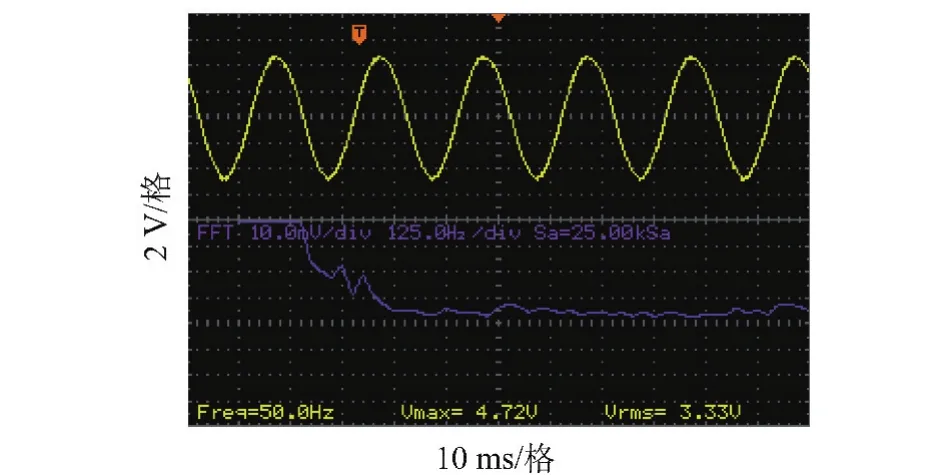
图13 滤波后输出相电压波形及谐波频谱Fig．13 The phase voltage and harmonic waveform spectrum after filtering

将MMC结构应用到高压变频器中,概述了高压变频器拓扑及工作机制,以逆变侧为分析对象,采用建模排序法控制电容电压稳定平衡,详细对比研究了几种不同调制算法的优劣,证明了POD-PWM法的优势,并针对该调制方法找出其最佳三角载波频率。最后,通过分析实验结果,证明了控制算法可行,被控子模块电容电压稳定,输出电压、电流畸变率低,谐波含量少,证明了POD-PWM与排序法电容电压平衡控制相结合的控制策略的有效性。

[1] 王琛琛,李永东．多电平变换器拓扑关系及新型拓扑[J]．电工技术学报,2011,26(1)：92-99．

Wang Chenchen,Li Yongdong．Multilevel converter topologies and two novel topologies[J]．Transactions of China Electrotechnical Society,2011,26(1)：92-99．

[2] 陶生桂,杨 超．二极管箝位式多电平逆变器PWM控制技术分析[J]．电力电子技术,2005,39(5)：8-10．

Tao Shenggui,Yang Chao．Analysis of PWM control technology for diode-clamping multi-level inverter[J]．Power Electronics,2005,39 (5)：8-10．

[3] Kou X,Corzine K A,Familiant Y L．A unique fault tolerant design for flying capacitor multi-level inverter[J]．IEEE Transactions on Power Electronics,2004,19(4)：979-987．

[4] 崔俊国,陶生桂．一种五电平逆变器SPWM控制方法的分析与仿真[J]．电气传动,2002,32(5)：18-22．

Cui Junguo,Tao Shenggui．A novel SPWM control strategy for fivelevel inverters[J]．Electric Drive,2002,32(5)：18-22．

[5] 刘景芳,杨荣峰,高 强,等．基于H桥级联变流器的功率单元设计[J]．电源学报,2011(4)：53-55．

Liu Jingfang,Yang Rongfeng,Gao Qiang,et al．Design of power unit based on cascaded H bridge converter[J]．Journal of Power Supply, 2011(4)：53-55．

[6] 刘 昂,欧阳红林,禹卫华,等．H桥级联型多电平高压变频器的实验研究[J]．电力电子技术,2009,43(2)：1-2．

Liu Ang,Ouyang Honglin,Yu Weihua,et al．The experimental study of H-bridge cascaded multilevel high voltage inverter[J]．Power Electronics,2009,43(2)：1-2．

[7] Marquardt R．Stromrichterschaltungen mit verteilten Ergiesspeichern [P]．German Patent：DE10103031A1,2001-01-24．

[8] Franquelo L G,Rodriguez J,Leon J I,et al．The age of multi-level converters arrives[J]．IEEE Industrial Electronics Magazine,2008, 2(2)：28-39．

[9] 韦延方,卫志农,孙国强,等．适用于电压源换流器型高压直流输电的模块化多电平换流器最新研究进展[J]．高电压技术, 2012,38(5)：1243-1252．

Wei Yanfang,Wei Zhinong,Sun Guoqiang,et al．New prospects of modular multilevel converter applied to voltage source converter high voltage direct current transmission[J]．High Voltage Engineering, 2012,38(5)：1243-1252．

[10] Munch P,Gorges D,Izak M,et al．Integrated current control,energy control and energy balancing of modular multilevel converters[A]．36th Annual Conference on IEEE Industrial Electronics Society [C]．Glendale：IEEE,2010．

[11] 管敏渊,徐 政．模块化多电平换流器型直流输电的建模与控制[J]．电力系统自动化,2010,34(19)：64-68．

Guan Minyuan,Xu Zheng．Modeling and control of modular multilevel converter in HVDC transmission[J]．Automation of Electric Power Systems,2010,34(19)：64-68．

[12] 管敏渊,徐 政,屠卿瑞,等．模块化多电平换流器型直流输电的调制策略[J]．电力系统自动化,2010,34(2)：48-52．

Guan Minyuan,Xu Zheng,Tu Qingrui,et al．Nearest level modulation for modular multilevel converters in HVDC transmission[J]．Automation of Electric Power Systems,2010,34(2)：48-52．

[13] 屠卿瑞,徐 政,正 翔,等．模块化多电平换流器型直流输电内部环流机理分析[J]．高压电技术,2010,36(2)：547-552．

Tu Qingrui,Xu Zheng,Zheng Xiang,et al．Mechanism analysis on the circulating current in modular multilevel converter based HVDC [J]．High Voltage Engineering,2010,36(2)：547-552．

[14] Angquist L,Antonopoulos A,Siemaszko D,et al．Inner control of modular multilevel converters-an approach using open-loop estimation of stored energy[A]．2010 International Power Electronics Conference[C]．Sapporo,2010．

[15] 王姗姗,周孝信,汤广福,等．模块化多电平电压源换流器的数学模型[J]．中国电机工程学报,2011,31(24)：1-8．

Wang Shanshan,Zhou Xiaoxin,Tang Guangfu,et al．Modeling of modular multi-level voltage source converter[J]．Proceedings of the CSEE,2011,31(24)：1-8．

[16] 吴洪洋．多电平变换器及其相关技术研究[D]．杭州：浙江大学,2001：50-51．

Control method and topology for high voltage frequency converter based on Modular Multilevel Converter

ZHENG Zheng,CUI Can,ZHANG Peng

(School of Electrical Engineering and Automation,Henan Polytechnic University,Jiaozuo 454000,China)

The fundamental concept of high voltage frequency converter based on Modular Multilevel Converter (MMC)was proposed．To investigate the inverter side,a mathematical model was built through the analysis of the topological structure and working mechanism of MMC．Subsequently the model was controlled by modeling sequencing method to achieve the goal of capacitor voltage stabilization and balancing．Through the comparisons with different methods,the advantage of carrier phase opposition disposition pulse width modulation(POD-PWM)was found．A simulation and experiment had been carried out using Matlab-simulink and Rt-Lab．The result shows that the converter works properly and the capacitor voltage is in a steady state．The output waveform contains few harmonic waves．Therefore the feasibility of POD-PWM and the voltage balancing control methods are verified by the experiment．The best frequency of triangle carrier wave is proposed herein．

high voltage frequency converter;Modular Multilevel Converter;modulation algorithms;voltage stabilization and balancing control;RT-Lab

TD611

A

0253-9993(2014)10-2128-06

2013-10-18 责任编辑：许书阁

国家自然科学基金资助项目(61340015,51077125)

郑 征(1965—),女,河南南阳人,教授。Tel：0391-3987556,E-mail：zhengzh@hpu．edu．cn

郑 征,崔 灿,张 朋．基于模块化多电平换流器的新型高压变频器拓扑及其控制[J]．煤炭学报,2014,39(10)：2128-2133．

10．13225/j．cnki．jccs．2013．1486

Zheng Zheng,Cui Can,Zhang Peng．Control method and topology for high voltage frequency converter based on Modular Multilevel Converter[J]．Journal of China Coal Society,2014,39(10)：2128-2133．doi：10．13225/j．cnki．jccs．2013．1486