隧道地震预报波场的有限元数值模拟

王朝令，刘争平，黄云艳，黄显彬

1.四川农业大学土木工程学院，成都 611830 2.西南交通大学土木工程学院，成都 610031

隧道地震预报波场的有限元数值模拟

王朝令1，2，刘争平2，黄云艳1，黄显彬1

1.四川农业大学土木工程学院，成都 611830 2.西南交通大学土木工程学院，成都 610031

在勘探地球物理领域中，能快速、有效地数值模拟2D和3D的地震全波场，包括同时模拟P波、S波、面波多分量波场特征的软件并不是很多；但在结构力学领域中，已有多种成熟的多波多分量有限元数值模拟大型商用软件用于求解弹性本构方程，如ANSYS，PLAXIS等。从方程结构来看，弹性本构方程与完全弹性波动方程相比，只多一项对时间的一阶微分项——阻尼项。因此，调整合理的介质参数——Rayleigh系数，令阻尼项近似为0，弹性本构方程就蜕化为完全弹性波动方程。隧道地震波场是在岩体中传播，具有弹性参数较好、无常规地震勘探中覆盖层等低速带干扰等的优点，采用ANSYS软件对隧道地震波场进行数值模拟，研究了频散、阻尼与吸收边界等数值模拟的相关技术。针对介质吸收，比较了数值模拟中有无阻尼的时间记录和波场快照，对隧道地震预报来说，将阻尼系数设定为0是一种合理的假设；比较了实例中不同网格长度与频散的关系，当网格长度小于波长的1/π倍时，才能消除频散；通过由波方程的推导，引入了黏弹性边界条件，通过实例计算证明它可以有效地吸收边界反射；最后对隧道地震预报进行了实例计算，算例表明采用ANSYS软件可以有效地模拟隧道复杂地质条件下全波场的激发传播过程。

数值模拟；ANSYS；有限元；隧道地震预报；地震波场；阻尼；频散；边界条件

0 引言

隧道属于地下建筑工程，其围岩地质情况复杂多变［1］，常遇到滑坡、崩坍、岩堆、岩洞、高应力高强度地层、松散地层、软土等不良地质地段，以及膨胀地层、含水未固结围岩、溶洞、断层、岩爆、流沙和瓦斯溢出地层等特殊地质地段，它们具有不同的性质、形状和规模，且成因和变异条件非常复杂，地质条件具有突发性。设计和勘察所提供的地质资料不可能自始至终符合实际情况，其详细程度也不能完全达到隧道施工的具体要求，如果没有可靠的超前地质预报，潜在的地质隐患就可能变成灾难。因此，隧道施工中安全和工程事故时有发生，轻则延长工期、增加投资，重则毁坏机械设备，甚至造成人员伤亡，而且事故处理难度大。在隧道地震超前预报方面：20世纪90年代初，瑞士Amberg测量技术有限公司基于地震波反射原理开发研制了一套超前预报系统设备——隧道地震预报（TSP）系统，可探测和预报围岩软硬变化，断层、破碎带、节理裂隙发育情况，含水、溶洞及围岩类别等［2］，TSP在瑞士、德国、法国、意大利、奥地利、日本等发达国家的隧道施工中，得到了广泛的应用；Hanson等［3］采用真反射成像法（true reneetion tomo，TRT），该方法在观测方式上采用的是空间多点接收和激发系统，检波器和激发的炮点呈空间分布，以充分获得空间波场信息，提高对前方不良地质体的定位精度。

地震模拟技术可以分为物理模拟和数值模拟2种［4］，数值模拟技术主要包括波动方程法和射线法两大类。射线法模拟精度较低；波动方程法实质是求解地震波波动方程，它能比较准确地模拟任意复杂介质中的地震波场，为研究地震波传播机理和复杂底层的解释提供更多的数学及物理依据。鉴于隧道地震波场的复杂性，开展波场数值模拟技术是非常有意义的。

常用的地震波场数值模拟方法主要包括有限差分法（FDM）、有限元法（FEM）等，目前大多采用基于有限差分的弹性或黏弹性双程波动方程进行计算。Boore［5］将有限差分法用于SH波非均匀介质地震波的CT成像模拟；Carcione等［6］提出了线性黏弹性介质中地震波传播的模拟方法；Talezcr等［7］进行了线性黏弹性介质中地震波传播的方法研究；Robertsson等［8］给出了黏弹性波有限差分模拟方法；Graves［9］给出了三维速度－应力方程交错网格有限差分法弹性波传播的模拟方法；Carcione等［10］研究了孔隙弹性介质中Biot纵波的数值模拟问题；Ozdenvar等［11］给出了孔隙弹性介质中地震波的交错网格有限差分模拟方法；Carcione等［12］提出了孔隙黏弹性介质中地震波传播的交错网格有限差分模拟方法；何樵登等［13］研究了横向各向同性介质中地震波数值模拟方法；王延光等［14］给出了一种适于强横向变速的高阶差分正演模拟方法；裴正林等［15］给出了三维任意各向异性介质中弹性波传播的交错网格高阶有限差分模拟方法；董良国［16］利用交错网格高阶差分方法对起伏地表情况下的弹性波传播进行了数值模拟；戴志阳等［17］利用褶积微分算子实现了对地震波场的数值模拟，并利用模型验证了其有效性和正确性；周晓华等［18］利用交错网格有限差分方法模拟了微动信号，结果表明采用这种方法得到的实测结果更符合实测结果。

这些方法具有较强的地震波传播模拟能力，也能很好地描述小尺度不均匀各向异性介质（岩层的孔隙、裂隙等）中地震波的传播特征。

在隧道波场数值模拟方面：Bohlen等［19－21］通过数值模拟在隧道中开展集成地震成像系统（ISIS）进行隧道超前预报，并通过3D有限差分的方法模拟了隧道超前预报，详细地模拟了隧道边墙上横波与面波的转换特征；刘晶波等［21］采用非线性有限元软件LS-DYNA模拟了爆破对隧道结构的影响，并与现场爆破进行了对比，证明模拟方法的有效性；鲁光银等［22］采用高阶交错网格差分方法进行了隧道超前预报的全波场数值模拟计算。

目前，在勘探地球物理领域中，能快速、有效地数值模拟2D和3D地震全波场，包括同时模拟P波、S波、面波多波多分量波场特征的软件，并不是很多。但在结构力学领域中，已有多种成熟的多波多分量有限元数值模拟软件用于解弹性本构方程，如ANSYS，PLAXIS等。从方程结构来看，弹性本构方程与完全弹性波动方程相比，只多一项对时间的一阶微分项——阻尼项。因此，调整合理的介质参数——Rayleigh系数，令阻尼项近似为0，弹性本构方程就蜕化为完全弹性波动方程。且这些软件中模拟震源可以用任意自定义数据加载，因此可方便地用现场实验和物理模拟提取的噪声震源函数加载模拟，显然比一般地球物理数值模拟中，主要用Ricker子波进行模拟更接近于实际情况。数值模拟中的关键技术是介质Rayleigh系数调整和吸收边界条件的合理加载。

在本文中，笔者首先引入弹性力学的本构、Cauchy、Navier3个基本方程，这3个方程涉及应力、应变和位移3个物理量，是弹性波传播理论中的基础方程；然后以这3个方程构建波动方程；最后基于由以上步骤的理论准备，利用ANSYS有限元软件实现对地震波场的数值模拟。

1 理论基础

人工地震中，当介质（即物体）受到非零的外力（如人工激发震源）时，该外力要转化为介质内部的应力，并使弹性介质内部发生应变和位移，形成地震波（即弹性波）场，介质的应力、应变以及能量的改变都是动态的运动过程。

1）本构方程的矩阵表达形式［23］为

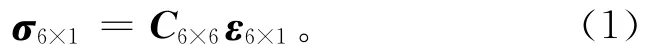
式中：σ6×1和ε6×1分别为单角标形式的应力和应变矩阵；C6×6是物性矩阵，也称为介质的弹性性质矩阵，它描述了介质的弹性和相关物理性质。

2）Cauchy方程的一维矩阵形式可以写成

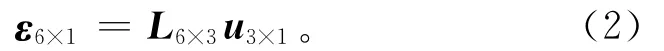
式中：u3×1是位移矩阵；L6×3是偏导数算符矩阵。

3）Naiver方程：

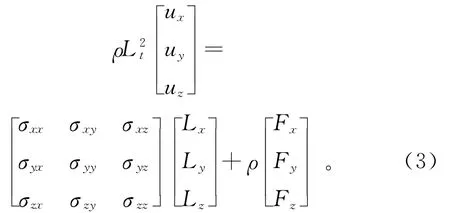
其中：ρ是介质密度；算符L2t表示对时间变量求二阶偏导 数；ux，uy，uz表 示x，y，z方 向 的 位 移；［LxLyLz］T＝［∂/∂x∂/∂y∂/∂z］T；［FxFyFz］T表示力矢量。式（3）就是振动介质的“平动运动方程”，即Navier方程。

将Cauchy方程（2）代入本构方程式（1），再将得到的方程式代入Navier方程式（3）得

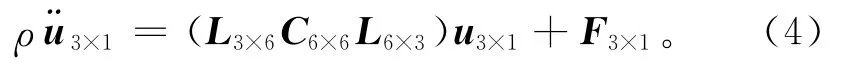
式中：位移矢量u的矩阵表达式为u3×1＝［uxuyuz］T；¨u3×1为节点的加速度矢量。式（4）即在外力作用下用位函数表示的波动方程。在地震波场中的外力就是震源的激发力，求解波动方程的问题就是波的传播问题。

在有限元求解中，存在下列矩阵微分方程：

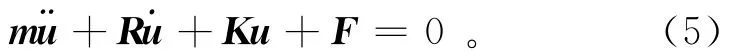
式中：m是质量矩阵；R是阻尼矩阵；K是刚度矩阵；˙u为节点速度矢量。式（5）是将单元刚度系数和单元力按照前面给出的方式相加得到的，而单元力包括外部力、初始应力等，此式相比于波动方程式（4）多了一个阻尼项R˙u，新的矩阵R和m也是按照一般方法由单元子矩阵组装得到的，即式中：Re与me分别是单元阻尼矩阵和单元质量矩阵；Ni为形状函数矩阵；μ为材料的黏滞矩阵；Ω为积分区域。

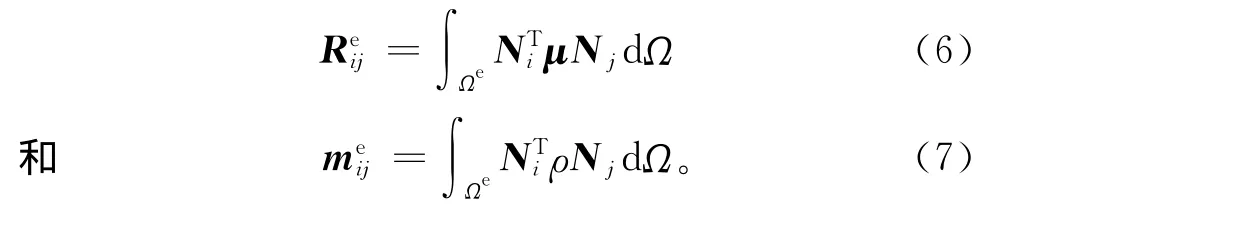
一般将式（5）定义的质量矩阵叫作一致性质量矩阵，是由Zienkiewicz和Cheung提出的［24］，其中的矩阵Re和R也称为一致性阻尼矩阵。在计算过程中，集中质量矩阵更方便、更高效。实际上，阻尼矩阵R很难确定，通常将阻尼矩阵定义为刚度矩阵和质量矩阵的线性组合，即

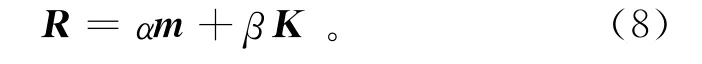
式中，质量阻尼系数α和阻尼刚度系数β可通过实验确定。这样的阻尼称为Rayleigh阻尼。

与波动方程式（4）形式类比，有限元问题方程（5）除去一阻尼项外，二者具有完全相同的形式，表明二者求解的弹性波场问题是等价的。

2 数值模拟实现策略

基于上述分析可知，瞬态动力学分析的基本方程式如式（5）所示，加入时间变量后变换为如下形式：

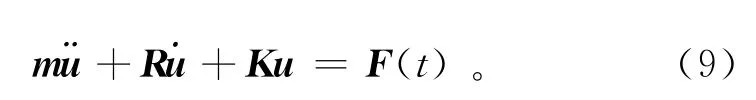
相比于式（5），将其中的力矩阵F变为荷载矢量F（t）。

在ANSYS软件中，采用Newmark时间积分方法（包括改进的算法HHT）和中心差分时间积分法求解瞬态动力学基本方程。

在采用ANSYS软件实现弹性波场模拟中，主要牵涉以下几个方面的问题：1）单元选择；2）介质吸收；3）频散效应；4）边界条件。下面分别进行讨论。

2.1 单元选择

由于计算机能力的限制，笔者首先研究2D的数值模拟，ANSYS中针对结构的二维单元包括Plane25、Plane42、Plane83、Plane182、Plane183。其中：Plane183是高阶二维八节点单元，具有二次位移项，适于生成不规则网格模型，因此不选用此单元；Plane25、Plane83均是谐响应对称单元，在本文研究的模型中，由于震源加载的限制，不能满足对此类单元加载载荷的要求，因此不选择此2种单元。比较之下，可供选择的平面单元只有2个：Plane42和Plane182。

Plane42和Plane182单元非常相近。Plane182单元具有选择简化积分这一选项，这对于不可压缩情况有助于防止网格被锁死；此外Plane182单元具有4个用户不可调节的自由度，相比于Plane42单元，在计算中具有较高的精确度。在本文模拟中，选择Plane182单元进行弹性波场的数值模拟。图1是在分别基于Plane42和Plane182单元采用相同震源激发等条件时接收到的地震记录，Plane182单元计算结果更好，但这种差异是比较微小的。

图1 不同单元数值模拟Fig.1 Modeling in different elements

2.2 介质吸收

ANSYS可以进行加载阻尼的运算。虽然笔者在本文中只研究弹性介质，不需要考虑阻尼因素，但当进行地震波场模拟时，需要考虑Rayleigh阻尼所造成的介质吸收问题，否则会出现意想不到的结果。据式（8）知，要计算Rayleigh阻尼，必须定义α和β；但一般情况下，α和β不能直接获得，通常由模态阻尼比ξ计算得出。模态阻尼比是特定振动模式下实际阻尼与临界阻尼的比值。若ωi是第i阶的自然圆频率，那么α和β满足如下关系式：

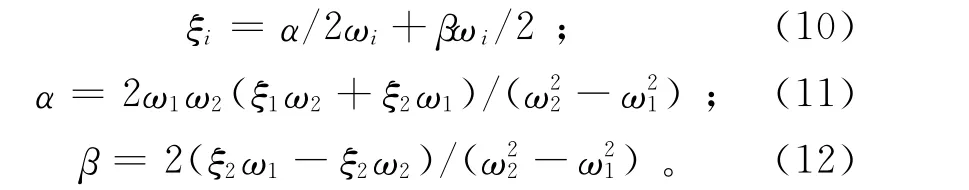
关于模态阻尼比ξ，不少文献中的研究表明取0.02～0.05是比较合适的；在一次模拟中，往往取一个常数；对于岩石等，一般取0.05。在许多实际问题中，往往忽略质量阻尼系数α。因此，将ωi＝2πfi代入式（11）可以得到

式中：f为频率。

若加载主频为100Hz，则由式（13）可以得到刚度阻尼系数β为1.59×10－4。大部分体系的刚度阻尼系数都是落在0～0.05这一范围的，在此范围内进行动力学计算时，位移的变化不超过5%；β为零时，系统的位移最大。因此，出于保守的目的，当系统承受冲击荷载时，取β为0是很合理的逼近。

下面通过数值计算来研究在加载阻尼系数β为1.59×10－4和0（即不加载阻尼系数）时的模拟效果。模型如图2所示，网格长度为0.5m，震源主频为300Hz，提取偏移距为10m、道间距1m的时间记录。

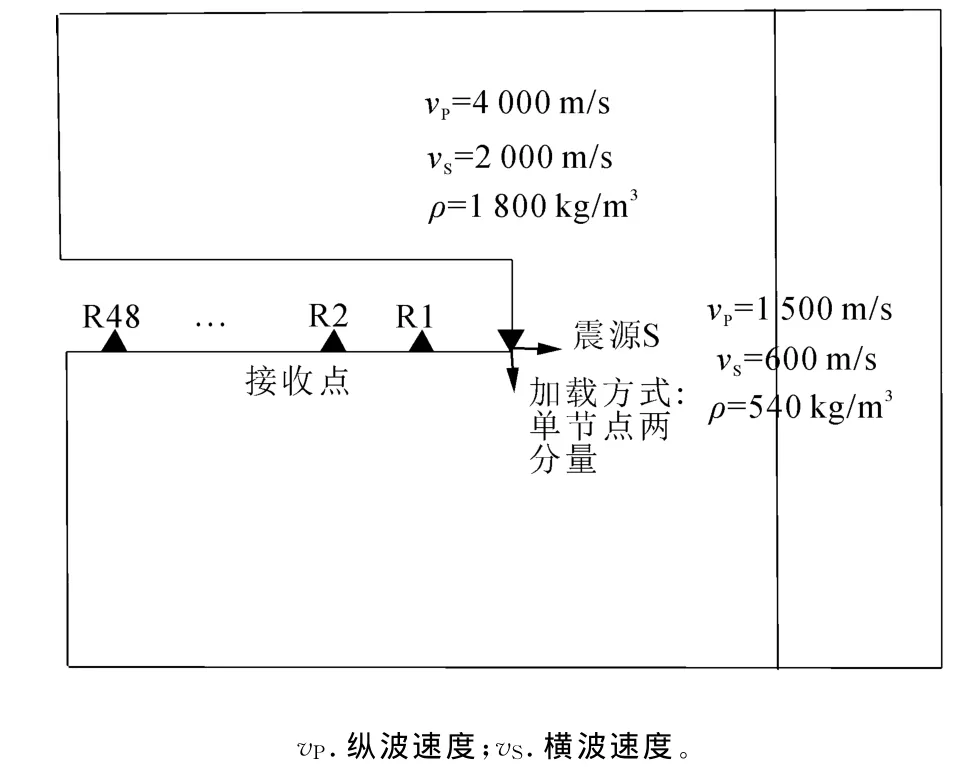
图2 阻尼加载模型图Fig.2 Model figure of damping loading

图3是加载阻尼和无阻尼情况下的波场快照。可以看出：2种情况下传播时的差异比较小，且相同时刻波场也非常接近；图3a中由于施加了阻尼，在波场扩散中能量不断减小，对比50ms时刻的波场快照尤其明显。

图4为提取的时间记录，用来比较加载前后的影响。由图4可以看出，加载阻尼和无阻尼的时间记录非常接近，无阻尼时得到的剖面信噪比更高，反射波的同相轴更清晰。

由此可见，ANSYS可以很好地模拟阻尼介质的波场。在地震超前预报的数值模拟中，将质量阻尼系数α和阻尼刚度系数β都设定为0。

2.3 网格剖分的频散效应

对模型进行网格划分时，由于要进行瞬态分析来模拟波场传播，必须考虑由于波长与网格长度所产生的频散效应，这主要取决于网格长度和时间步长的大小。从波动力学带宽定理［25］得到

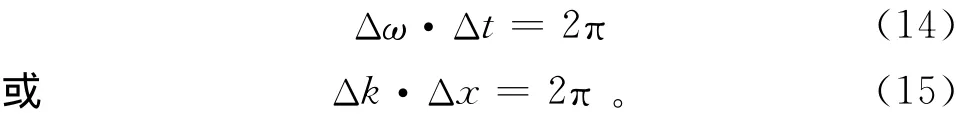
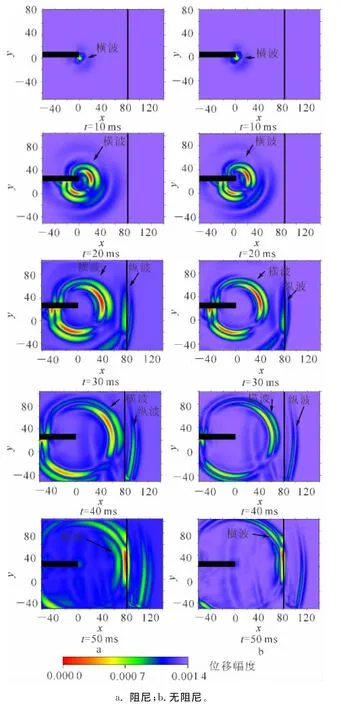
图3 阻尼波场快照Fig.3 Snapshot of damping

式中：k为波数；Δt为时间步长；Δx为网格长度。式（15）表明，能量所在空间或时间越集中，其频谱就越宽。

国内外有不少学者从不同角度提出离散化准则，如 Kausel［26］，Costantino等［27］和 Miller等［28］分别给出：

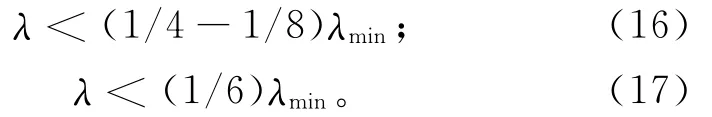
式中：λ为波长；λmin为最小波长。

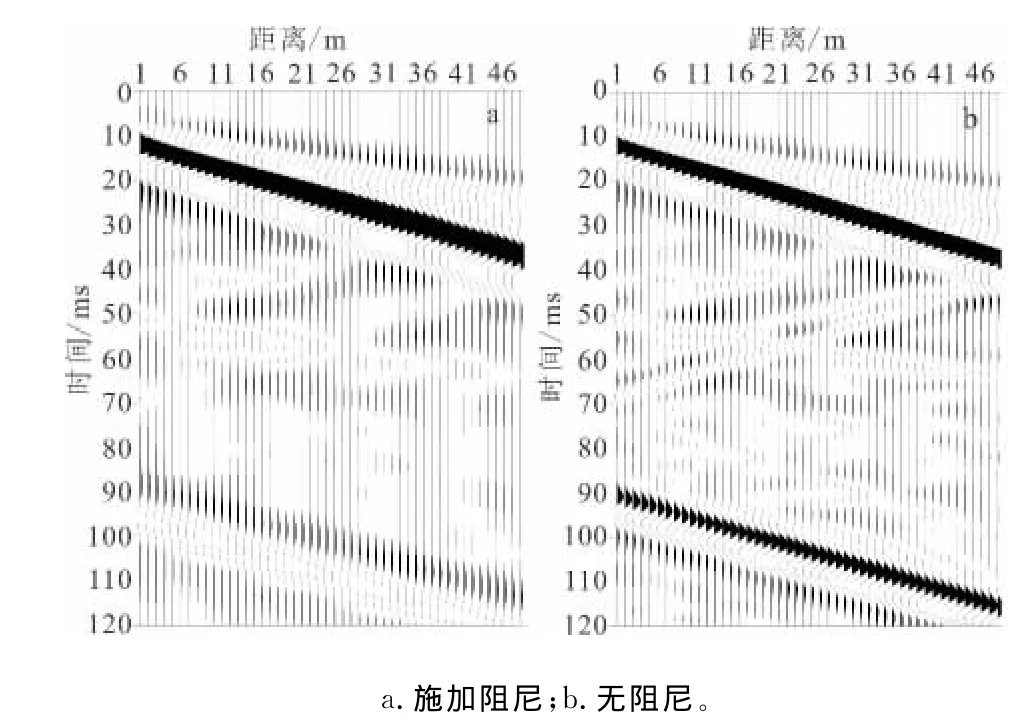
图4 阻尼加载时间记录Fig.4 Time recording of damping loading

据宗福开［25］的研究结果，由λmin＝v/fmax（v为速度，fmax为最高频率），当波在传播方向划分的网格数n大于10时，则得出有限元离散化准则为

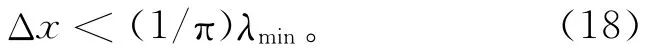
式（18）具有明确的物理意义，即要求网格长度小于波长的1/π倍。应当指出，根据波传播边界条件的性质，通常Δx≤（1/π～1/8）λmin。

据以上结论，笔者进行了网格长度不同的有限元数值模拟，模型示意图如图5所示。为减小边界对模拟结果的影响，模型4个边界均加载黏弹性吸收边界。模型背景设定横波波速为2 000m/s，纵波波速为4 000m/s，密度为1 800kg/m3。由实际资料分析，震源主频取300Hz。由于横波的波长较纵波的小，故模型的λmin取为横波的主波长，约为20 m。分别设定网格长度为10.0、5.0、2.5、1.0和0.5 m，分析波场数值模拟的频散效应。

图6是不同网格长度、同一节点的位移数值。根据公式（15），当网格长度为10.0m＞20/π＝6.366m时，波场的位移数值解震荡很严重。随着网格长度越来越短，波的震荡现象逐渐减弱。当网格长度为5.0m时，相比于10.0m的计算值，波的震荡变小了；当网格长度为2.5m时，仍然存在轻微的震荡；当网格长度由1.0m进一步变小到0.5 m时，模拟计算结果并没有太大的改进。考虑到计算量的问题，对于实际模型模拟时，采用最大网格长度为1.0m的剖分网格就可以最大程度地减小频散效应，很好地模拟波场的传播了。因此，在进行模拟时，按照式（18）所要求的网格长度进行划分，即可消除频散的影响。

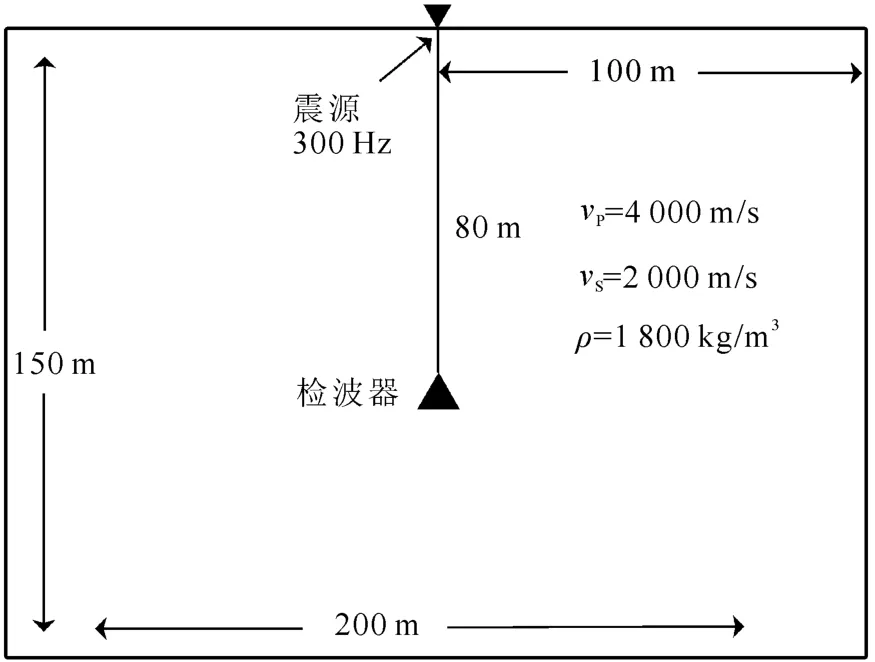
图5 网格剖分模型图Fig.5 Model figure of grid meshing

图6 采样点位移随网格长度变化图Fig.6 Displacement of sampling point varied with meshing

2.4 边界条件

采用有限元模拟时，通常采用时间域的吸收边界，这种边界由一维或二维条件导出，并使得没有能量从边界反射。其中：应用最广泛的是Lysmer等［29］引入的黏弹性边界，它采用黏弹性阻尼来代替远场边界；Novak等［30］提出了平面应变边界，这种边界主要应用到嵌入基础和桩基中。但是，平面应变边界包含依赖于频率的项，这在加载瞬态载荷的瞬态响应分析中会变得比较复杂；相比之下黏弹性边界应用更广泛，加载简单，且对整个计算所增加的计算量可以忽略不计，在采用黏弹性边界时，极少会产生这种反射。

当波穿过介质时，波前的应力产生在法向和切向2个分量上。假定在平面应力条件下，径向位移的波动方程为［31］

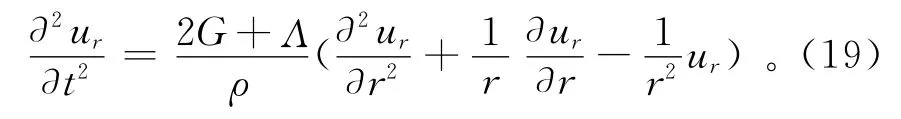
其中：ur表示径向位移；G为压缩模量；r为半径；Λ为Lame常数。

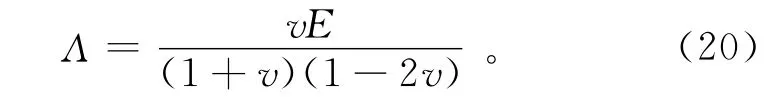
式中：E为Young模量；v是Possion比。

将径向位移ur用位移势函数φ表示：

则式（19）可表示为

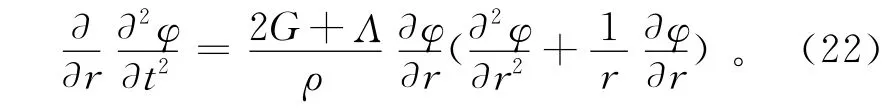
两边都对径向r进行积分，则波方程用φ表示为

可以得到估计表达式：

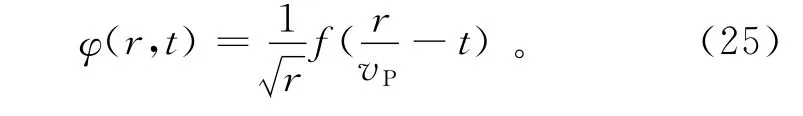
用f′表示频率f的导数，则径向位移ur、径向应力σr、径向应变εr、横向应变εθ可以用频率f和半径r表示：

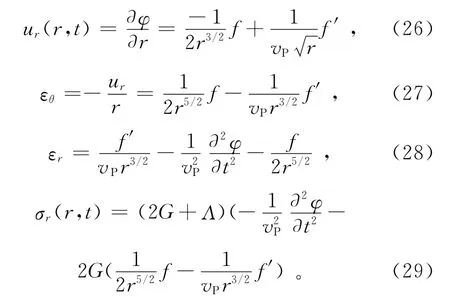
对于任意的半径rb，对频率f的任意时刻导数都是其对幅角导数的相反值，则半径rb处的位移值、速度值和加速度值可以表示为

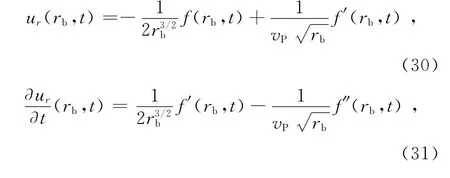
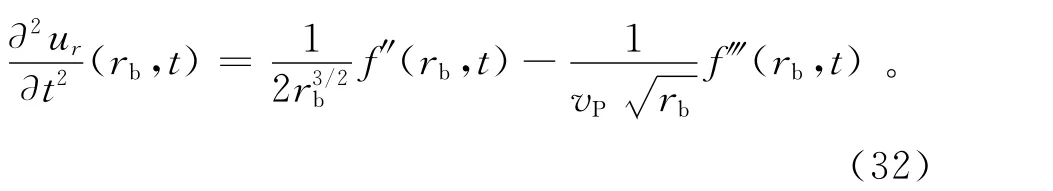
在半径rb处二阶时间导数为

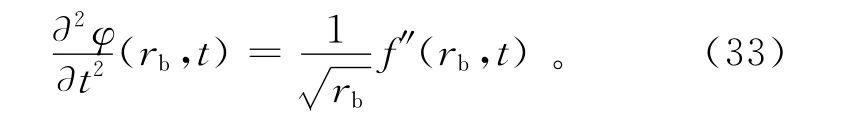
将式（33）代入式（29）可以得到f（rb，t）在边界的应力：

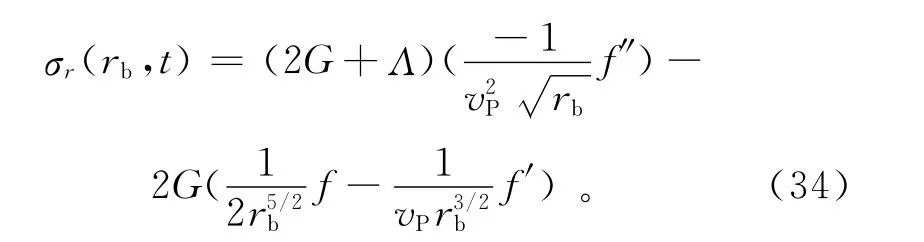
对式（34）做时间微分：

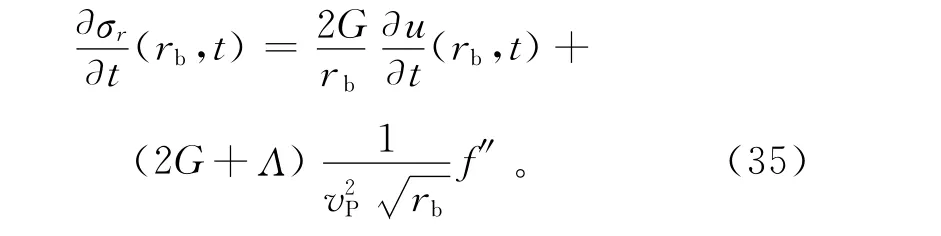
联立式（34）和式（35），可以消去未知函数f：

此种在有限元中集合时间的边界，在实现中，若采用弹簧形式将会非常方便。Wolf［32］提供了如图7所示的弹簧。

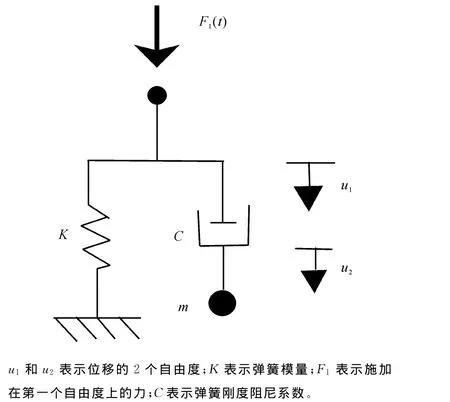
图7 弹簧模型Fig.7 Spring model

图7中弹簧模型的波动方程如下：

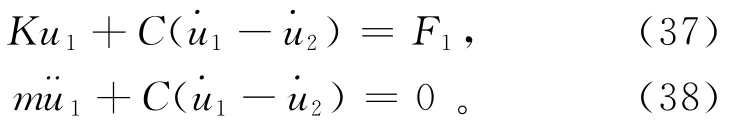
由式（37）可以得到

式（39）对时间求导：

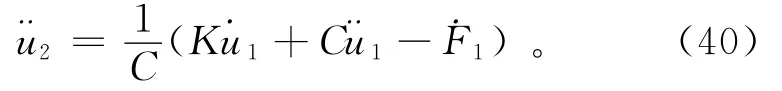
将式（39）和式（40）代入到式（38）可以得到第一个自由度的波动方程：

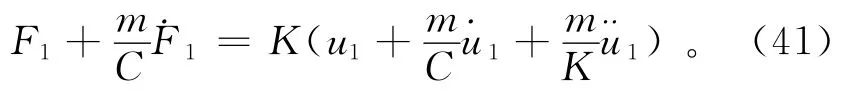
联立式（36）—式（41）可以得到等价的刚度、阻尼和质量：

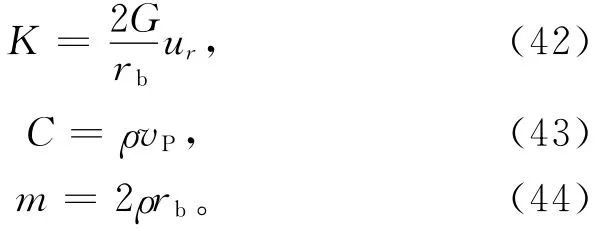
可以将式（42）（43）（44）所得的值赋予弹簧，来实现黏弹性边界。

归纳二维人工边界等效物理系统的弹簧系数K和阻尼系数C在针对不同边界时分别如下。

切向边界：

法向边界：

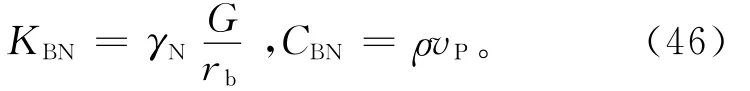
式中：KBN、KBT分别为弹簧的法向与切向刚度；CBT、CBN分别为弹簧的法向与切向阻尼；rb为波源至人工边界点的距离；γT和γN分别为切向与法向黏弹性人工边界参数。根据刘晶波等［33］的研究结果，人工边界比较合适的参数γT取值范围为［0.35，0.65］，γN的取值范围为［0.8，1.2］。

在ANSYS软件中，适合用来做黏弹性边界的单元选用Combin14，它在1维、2维或3维应用中具有轴向或扭转的性能。纵向阻尼弹簧是单轴压缩张力的单元，在每个节点有3个自由度：x、y和z轴。不考虑扭转和弯曲，另外弹簧阻尼单元没有质量矩阵，图8为Combin14单元的示意图和此单元在ANSYS数值模拟计算中的加载方式。

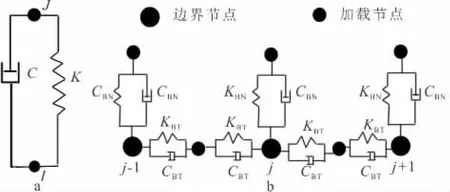
图8 Combin14单元示意图（a）和边界加载方式（b）Fig.8 Combin14unit schematic（a）and boundary loading mode（b）

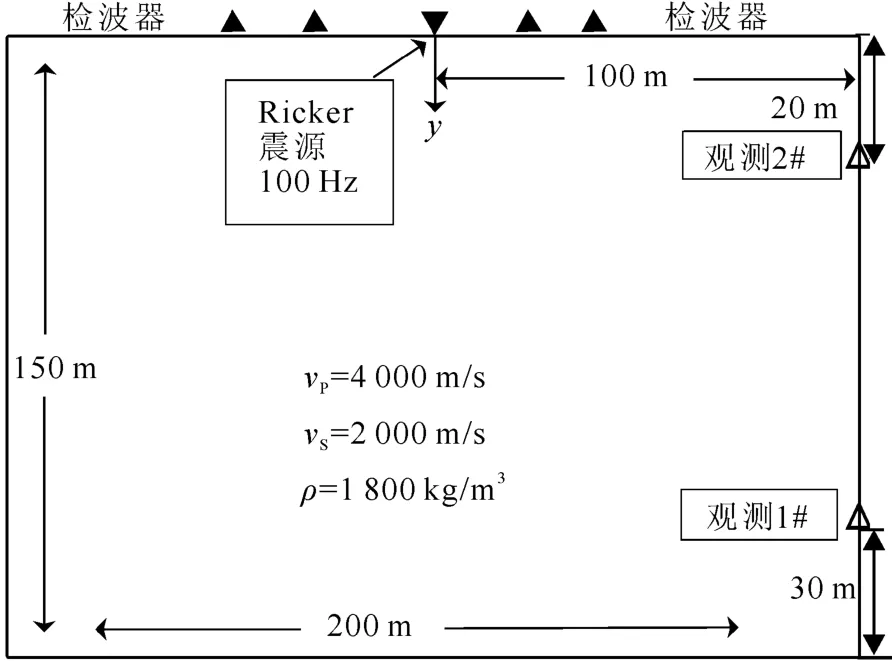
图9 边界比较模型图Fig.9 Model figure of boundary comparing

按照式（19）和式（21）将Combin14在模型周边布设，利用如图9所示的模型计算四周是Dirichlet边界和黏弹性边界的数值模拟。震源为100Hz的Ricker子波，加载方向竖直向下，网格长度0.5m，观测系统以震源为中心，两边等间距，道间距为2 m，道数为48道，分别取得震源两边的时间记录，如图10所示。

在模型四周施加了黏弹性边界时，直达P波和直达S波都受到了抑制，且相较之下，S波受影响更大。这是由于黏弹性边界弹簧的存在使除直达P、S波之外的边界反射被吸收的缘故，证明了黏弹性边界可以有效地吸收反射。在默认位移为0的Dirichlet边界所得到的记录中（图11），各边界的反射波返回到接收排列，使得对波的辨识和同相轴的判别都变得比较困难。由图10时间记录和图11波场快照的相同时刻的对比可以看出，Dirichlet边界的波场快照中各种反射波夹杂在一起，使得波场变得非常复杂，不易辨识，增加了波场分析的难度。

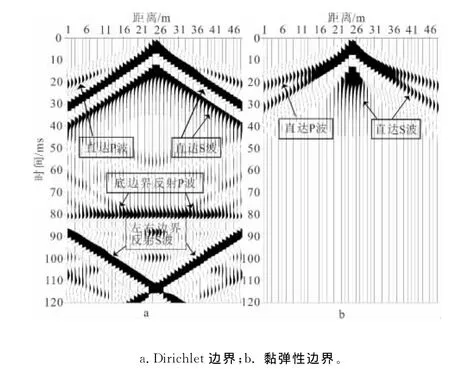
图10 2种边界的时间记录Fig.10 Time record of two boundaries

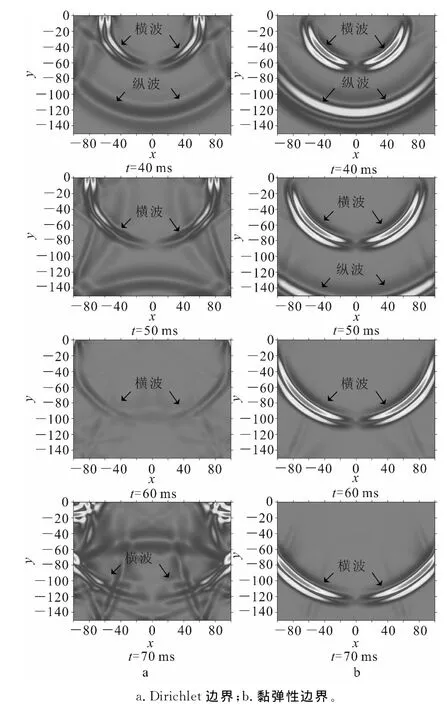
图11 2种边界的波场快照Fig.11 Wavefield snapshot of two boundaries

3 计算实例

图12为边墙激发二维隧道数值模型。模型隧道开挖工作面前方具有一模拟断层垂直倾角的低波阻抗反射带。隧道模型区域I中的纵、横波速度分别设为4 000m/s和2 000m/s，低波阻抗区域II的纵、横波速度为2 000m/s和1 000m/s，另一侧区域III的纵、横波速度设为3 000m/s和1 500m/s；其观测系统中激发震源位于边墙上，接收排列的48道检波器也设置在边墙上，并与震源在同一直线上，最小偏移距10m，道间距1m。由互换原理可知，若将接收与激发换位，即为TSP观测系统。模拟震源为主频300Hz的Ricker。采样间隔为0.1ms，采样视窗长0.1s，网格长度0.5m。模型边界均采用黏弹性边界条件。

图12 边墙激发数值模型Fig.12 Numerical model of sidewall excited

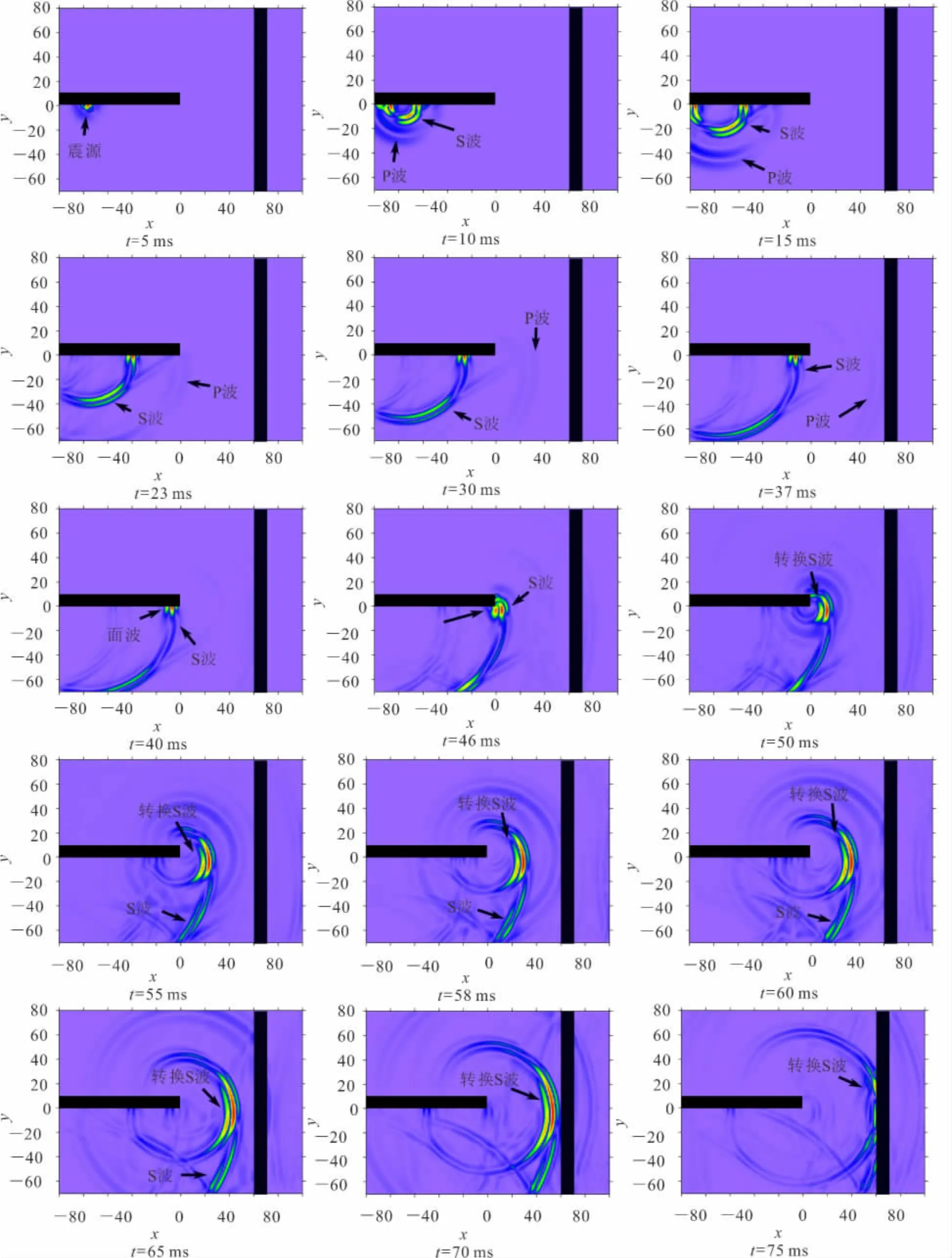
图13 实例波场快照Fig.13 Snapshot of the example

图13是边墙激发所产生的波场快照。由图13可见，震源激发的横波能量远大于纵波能量，所以波场快照中纵波传播和反射特征表现不如横波那么明显。由图13分析，P波和S波的隧道波场特征有很大的差异，因此对二者的特征分述如下。首先，当t＝5ms时，传播中的P、S波还没有完全分离；t＝10ms、t＝15ms时，由于P波比S波速度快，二者已经完全分离。对于P波：当t＝23ms时，P波传播到掌子面；t＝30ms时，P波经过掌子面，并继续向前方介质传播；t＝37ms时，P波到达第一波阻抗变化界面，部分能量反射回来，另一部分则透射过界面继续向前传播，反射回来的P波将会被沿边墙布置的检波器观测排列接收。对于S波，激发的S波一部分能量以体波的形式向边墙外的介质体内传播，另一部分能量则转换为瑞利（Rayleigh）面波，沿边墙向前传播。t＝40ms时，S波到达掌子面。t＝46ms、t＝50ms时，瑞利面波的部分能量在掌子面转换为S波，新产生的S波以体波的波阵面继续向前传播［20］，部分能量则继续以面波的波阵面沿边墙向后传播，可被沿边墙布置的检波器观测排列接收。这类来自于掌子面的反射面波被称为SRR波，显然对于提取掌子面前方介质的反射S波信息来看，是干扰波。t＝55ms、t＝58ms时，转换S波继续向前传播，直到t＝75ms时刻，转换S波到达第一反射界面，部分能量发生反射回传，部分发生透射继续向前传播。反射回传的S波到达隧道边墙时，部分能量将再次转换为面波，并会被沿边墙布置的检波器观测排列接收。分析表明，隧道边墙激发条件下，观测排列记录的反射S波实际上是由S波转换为面波，面波再转换为S波，最后再转换为面波的复杂转换波，被称为SRSR波。波场快照还显示，SRSR波的能量远大于反射P波。

图14是边墙激发数值模型位移x分量、y分量的时间记录。图14中的同相轴主要包括反射纵波、反射横波和面波转换横波，与图13的波场快照相对应，图14中的负视速度同相轴就是面波在掌子面转换为横波传播到接收排列所形成的同相轴SRSR波。

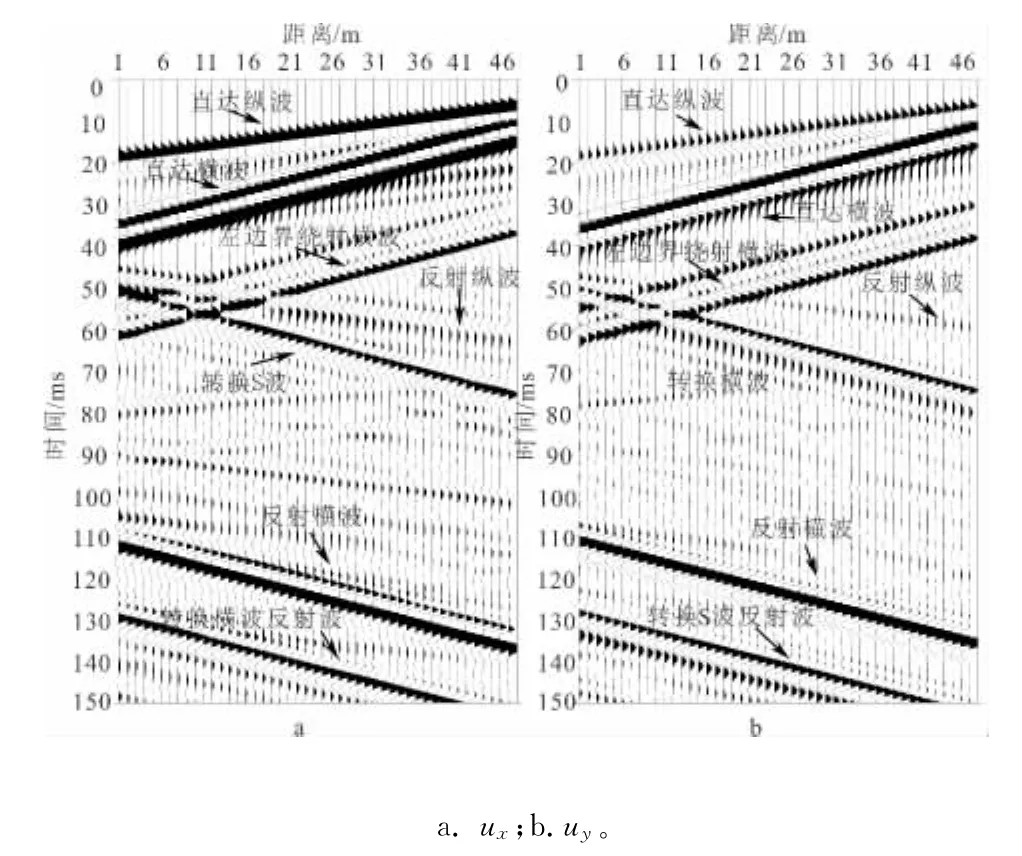
图14 实例时间记录Fig.14 Profiles of the example

以上分析表明，有限元数值方法可以有效地模拟隧道复杂地质条件下的全波场的激发传播过程。

4 结论

1）由于隧道地震预报的波场传播主要是在岩体中进行，相比于常规地面地震勘探，具有更好的弹性参数。对隧道地震波场的模拟而言，将质量阻尼系数α和阻尼刚度系数β都设置为0是比较合理的近似，能满足数值模拟的需要；若模拟地表地震勘探，则需要考虑介质阻尼。

2）针对网格长度，为满足计算要求，根据网格长度不大于（1/π～1/8）λmin的原则，针对主频为300 Hz的震源而言，取网格长度为1m就可以消除频散效应的影响。

3）加载黏弹性边界条件可以很好地吸收边界反射，并且其有良好的鲁棒性。

4）算例表明，采用大型有限元软件可以有效地模拟隧道复杂地质条件下的全波场的激发传播过程。

5）本文只是对二维隧道地震波场进行了数值模拟研究，相比于实际需求，开展三维隧道地震波场的数值模拟研究更具实际意义。

本文采用数值模拟方法虽然只研究了隧道地震反射波场的传播规律，根据不同模型，它也可以模拟地震勘探领域中其他地震波场的传播规律，这为地震波场的数值模拟提供了一种解决手段。

（References）：

［1］鲁光银.隧道地质灾害反射波法探测数值模拟及围岩f－Ahp分级研究［D］.长沙：中南大学，2009.

Lu Guangyin.Numerical Simulation for Tunnel Geological Hazard Detection by Reflected Wave Method and Rock Dynmanic Classification by f-Ahp Method Research［D］.Changsha：South China University，2009.

［2］刘志刚，刘秀峰.TSP隧道地震勘探在隧道隧洞超前预报中的应用与发展［J］.岩石力学与工程学报，2003，22（8）：1399-1402.

Liu Zhigang，Liu Xiufeng.TSP Application and Development in Tunnel Lead Forecast［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22（8）：1399-1402.

［3］Hanson D R，Haramy K Y，Neil D M.Seismic Tomography Applied to Site Characterization［M］.Denver：American Society of Civil Engineers，2000.

［4］佘德平.波场数值模拟技术［J］.勘探地球物理进展，2004，27（1）：16-21.She Deping.On Wave Field Numerical Modeling Techniques［J］.Progress in Exploration Geophysics，2004，27（1）：16-21.

［5］Boore D M A.Note on the Effect of Simple Topography on Seismic SH Waves［J］.Bulletin of the Seismological Society of America，1972，62（1）：275-284.

［6］Carcione M，Kosloff，Kosloff R.Wave Propagation Simulation in a Linear Viscoelastic Medium［J］.Geophysical Journal，1988，95（3）：597-611.

［7］Talezer H，Carcione J M，Kosloff D.An Accurate and Efficient Scheme for Wave-Propagation in Linear Viscoelastic Media［J］.Geophysics，1990，55（10）：1366-1379.

［8］Robertsson.Numerical Free-Surface Condition for Elastic Viscoelastic Finite-Difference Modeling in the Presence of Topography［J］.Geophysics，1996，61（6）：1921-1934.

［9］Graves R W.Simulating Seismic Wave Propagation in 3DElastic Media Using Staggered-Grid Finite Differences［J］.Bulletin of the Seismological Society of America，1996，86（4）：1091-1106.

［10］Carcione J，Quiroga-Goode G，Cavallini F.Wavefronts in Dissipative Anisotropic Media：Comparison of the Plane-Wave Theory with Numerical Modeling［J］.Geophysics，1996，61（3）：857-861.

［11］Ozdenvar T，McMechan G.Algorithms for Staggered-Grid Computations for Poroelastic，Elastic，Acoustic，and Scalar Wave Equations［J］.Geophysical Prospecting，1997，45（3）：403-420.

［12］Carcione J，Helle H.Numerical Solution of the Poroviscoelastic Wave Equation on a Staggered Mesh［J］.Journal of Computational Physics，1999，154（2）：520-527.

［13］何樵登，张中杰.3D横向各向同性介质中的体波［J］.石油地球物理勘探，1990，25（2）：137-147.

He Qiaodeng，Zhang Zhongjie.3DTransversely Isotropic Medium Body Wave［J］.Oil Geophysics Exploration，1990，25（2）：137-147.

［14］王延光，李振春，穆志平，等.一种适于强横向变速的高阶差分正演模拟方法［J］.石油大学学报：自然科学版，2002，26（5）：37-39.

Wang Yanguang，Li Zhenchun，Mu Zhiping，et al.A High-Order Finite-Difference Forward-Modeling Fit for Strong Lateral Velocity Variation［J］.Journal of the University of Petroleum，China，2002，26（5）：37-39.

［15］裴正林.地震波标量方程的小波自适应网格有限差分法数值模拟［J］.石油地球物理勘探，2005，40（3）：267-272.

Pei Zhenglin.Wavelet Scalar Adaptive Mesh Seismic Wave Equation Finite Difference Numerical Simulation［J］.Oil Geophysics Exploration，2005，40（3）：267-272.

［16］董良国.复杂地表条件下地震波传播数值模拟［J］.勘探地球物理进展，2005，28（3）：187-194.

Dong Liangguo.Complex Surface Conditions Numerical Simulation of Seismic Wave Propagation［J］.Progress in Exploration Geophysics，2005，28（3）：187-194.

［17］戴志阳，孙建国，查显杰.地震波场模拟中的褶积微分算子法［J］.吉林大学学报：地球科学版，2006，35（4）：520-524.

Dai Zhiyang，Sun Jianguo，Zha Xianjie.Seismic Wave Field Modeling with Convolutional Differentiator Algorithm［J］.Journal of Jilin University：Earth Science Edition，2006，35（4）：520-524.

［18］周晓华，陈祖斌，曾晓献，等.交错网格有限差分法模拟微动信号［J］.吉林大学学报：地球科学版，2012，42（3）：852-857.

Zhou Xiaohua，Chen Zubin，Zeng Xiaoxian，et al.Simulation of Microtremor Using Staggered-Grid Finite Difference Method［J］.Journal of Jilin University：Earth Science Edition，2012，42（3）：852-857.

［19］Bohlen T.Parallel 3-D Viscoelastic Finite Difference Seismic Modelling［J］.Computers ＆ Geosciences，2002，28（8）：887-899.

［20］Bohlen T，Lorang U，Rabbel W，et al.Rayleigh-to-Shear Wave Conversion at the Tunnel Face：From 3D-FD Modeling to Ahead-of-Drill Exploration［J］.Geophysics，2007，72（6）：67-79.

［21］Liu Jingbo，Yan Qiushi，Wu Jun.Analysis of Blast Wave Propagation Inside Tunnel［J］.Transactions of Tianjin University，2008，14（5）：358-362.

［22］Lu Guangyin，Han Xuli，Zhu Ziqiang.A Staggered-Grid High-Order Finite Difference Numerical Simulation for Tunnel Seismic Prediction Ahead of Construction［J］.Engineering Computation，2009，23（2）：225-228.

［23］牛滨华.半空间均匀各向同性单相固体弹性介质与地震波传播［M］.北京：地质出版社，2005：200-205.

Niu Binhua.Single-Phase Half-Space Homogeneous Isotropic Elastic Solid Medium and Seismic Wave Propagation［M］.Beijing：Geological Publishing House，2005：200-205.

［24］Cheung Y K，Jin W G，Zienkiewicz O C.Direct Solution Procedure for Solution of Harmonic Problems Using Complete，Non-Singular，Trefftz Functions［J］.Communications in Applied Numerical Methods，1989，5（3）：159-169.

［25］宗福开.波传播问题中有限元分析的频散特性及离散化准则［J］.爆炸与冲击，1984，4（4）：16-23.

Zong Fukai. Frequency-Dispersion Characteristics and Dicretization of the Finite Element Analysis in Wave Propagation Problems［J］.Explosion and Shock Waves，1984，4（4）：16-23.

［26］Kausel E.Local Transmitting Boundaries［J］.Journal of Engineering Mechanics，1988，114（6）：1011-1027.

［27］Costantino C，Miller C，Lufrano LA.Soil Structure Interaction Parameters from Finite Element Analysis［J］.Nuclear Engineering and Design，1976，38（2）：289-302.

［28］Miller T F，Schmidt F W.Use of a Pressure Weighted Interpolation Method for the Solution of the Incompressible Navier-Stokes Equations on a Nonstaggered Grid System［J］.Numerical Heat Transfer：Part A：Applications，1988，14（2）：213-233.

［29］Lysmer J，Kuhlemeyer R L.Finite Dynamic Model for Infinite Media［J］.Journal of Engineering Mechanics，1969，95（4）：859-877.

［30］Novak M，Hindy A.Seismic Analysis of Underground Tubular Structures［C］//Proceedings of the 7th World Conference on Earthquake Engineering.Istanbul：Ankara Natl Common Earthquake Eng，1980：287-294.

［31］Deeks J，Randolph M.Axisymmetrical Time-Domain Transmitting Boundaries［J］.Journal of Engineering Mechanics-Asce，1994，120（1）：25-42.

［32］Wolf J P.A Comparison of Time-Domain Transmitting Boundaries［J］.Earthquake Engineering ＆Structural Dynamics，1986，14（4）：655-673.

［33］刘晶波，谷音，杜义欣.一致粘弹性人工边界及粘弹性边界单 元 ［J］.岩 土 工 程 学 报，2006，28（9）：1070-1076.

Liu Jingbo，Gu Yin，Du Yixin.Consistent Viscous-Spring Artificial Boundaries and Viscous-Spring Boundary Elements［J］.Chinese Journal of Geotechnical Engineering，2006，28（9）：1070-1075.

Wavefield Modeling Based on the Finite Element Method for the Tunnel Seismic Prediction

Wang Zhaoling1，2，Liu Zhengping2，Huang Yunyan1，Huang Xianbin1

1.CollegeofCivilEngineering，SichuanAgricultureUniversity，Chengdu611830，China
2.CollegeofCivilEngineering，SouthwestJiaotongUniversity，Chengdu610031，China

In the field of exploration geophysics，the software packages that can fast and efficiently simulate 2Dand 3Dseismic full-wavefield，including simultaneously simulate P-wave，S-wave，and surface wave are not very much.In the structure mechanics，however，many sophisticated commercial software packages based on the finite element method including ANSYS and PLAXIS for multi-wave and multi-component have been employed for the solutions of the elastic constitutive equations.Compared to the complete elastic wave equations，the elastic ones include a damping term，which is a first-order differential term time.Therefore，by adjusting the parameter of the medium，that is，the Rayleigh coefficient to make the damping to zero，the elastic constitutive equations will degenerate into full elastic wave equation.The wavefields propagating in the rocks of a tunnel are free of the disturbance of low velocity resulting from the cover layer in the conventional seismic exploration.We simulated the wavefields of the tunnel seismic prediction using the ANSYS software，and researched the dispersion，damping and absorbing conditions etc.in the numerical modeling.For medium absorption，we compared time records and snapshots of the wavefields in the numerical simulation for the cases with and without the damping.In the tunnel seismic prediction，setting the damping to zero is a reasonable assumption.By comparing the relation of different grid length and dispersion in the numerical example，we find that the dispersion disappears when the mesh size is smaller than the wavelength of 1/π.By introducing a viscoelastic boundary condition deduced from the wave equation，boundary reflections can be effectively absorbed.Finally，an numerical example of the tunnel seismic prediction shows that the usage of the ANSYS software can effectively simulate the propagation of waves in the complicated geological conditions.

numerical modeling；ANSYS；FEM；tunnel seismic prediction；seismic wavefield；damping；dispersion；boundary condition

10.13278/j.cnki.jjuese.201404305

P631.4

A

王朝令，刘争平，黄云艳，等.隧道地震预报波场的有限元数值模拟.吉林大学学报：地球科学版，2014，44（4）：1369-1381.

10.13278/j.cnki.jjuese.201404305.

Wang Zhaoling，Liu Zhengping，Huang Yunyan，et al.Wavefield Modeling Based on the Finite Element Method for the Tunnel Seismic Prediction.Journal of Jilin University：Earth Science Edition，2014，44（4）：1369-1381.doi：10.13278/j.cnki.jjuese.201404305.

2013-12-12

国家自然科学基金项目（40874051）

王朝令（1980—，男，讲师，博士，主要从事地震波场数值模拟、隧道超前预报预报研究，E-mail：wong81010＠gmail.com。