城市购物出发时间的非参数生存分析

李明，杨小宝，环梅，董苓

（北京交通大学交通运输学院，北京 100044）

城市购物出发时间的非参数生存分析

李明，杨小宝，环梅，董苓

（北京交通大学交通运输学院，北京 100044）

根据济南市2011年的出行数据，研究了该市城市购物出发时间的分布特性。采用生存分析方法，建立城市购物出发时间的持续时间模型。运用非参数方法，对购物出发的持续时间进行估计，讨论了城市购物出行的时间分布和家庭社会经济属性变量对购物出发时间的影响。结果表明，总体样本的5.4%在7：00之前出发购物，69.7%在7：00～10：00出发购物，在10：00之后出发购物的少于24.9%。性别、年龄和家庭中儿童的数量对购物出发时间的选择有着显著的影响。女性比男性购物出发早，老年人更易在非高峰期进行购物出行，没有儿童的家庭购物出行在时间上更加灵活。本研究为购物出行的定量研究提供了准确、有效的分析工具，也对通过动态价格机制控制交通拥堵有重要意义。

城市购物出发时间；连续时间模型；非参数生存分析

在城市发展过程中，交通系统和城市发展相互影响，相互制约。而个人的出行选择对城市交通有非常重要的影响，对个体出行行为的研究，是进行城市交通规划、建设和管理的一项不可缺少的基础工作［1］。研究个人出行的目的是为了改善个人出行计划和提出有效的交通管理措施。根据基于活动的出行理论，出行可以看作为到达活动空间的必要方式，这意味着出行时间的重要性［2］。因此，在构造与出行有关的模型时，活动的出发时间是一个重要的因素。

现有对出行的研究主要集中在对通勤者的研究方面，通勤者的出发时间一般是在一天中的高峰拥堵时段。通勤出行是城市居民最基本和最重要的出行，影响到城市生活的方方面面，特别是早、晚高峰通勤时段的交通拥堵，已成为城市交通最为突出的问题之一，并制约着城市社会和经济的进一步发展。然而，目前对非通勤者出行研究较少，由于非通勤出行在城市出行中所占比重越来越大，且非通勤出行比通勤出行时间上更加灵活，这意味着社会人口学变量的变化和交通控制措施对非通勤出行时间的影响要多于不太灵活的通勤出行，所以有必要对非通勤者出行进行深入研究。以前的研究多采用logit离散模型，将时间分成若干时段［3－6］，这样的方法虽具有一定的科学性，但是将出发时间作为离散的变量，而不是连续的变量。另外，当划分时间的方法不同时，就会出现不同的结果，很难对交通状况做出正确的评价。

在众多非通勤出行活动中，购物出行是一个重要的出行目的。本文主要对非通勤出行人群中的购物人群的出发时间进行研究。基于济南市2011年工作日一天中居民出行的调查数据，主要探讨了购物出发时间的整体分布特征，利用生存分析方法，构造了购物出发时间的选择模型，并从变量的显著性检验方面，讨论并分析了对购物出发时间有显著影响的社会经济属性变量。本研究将为制定拥挤收费、错时上班等交通需求管理措施，提供重要的参考依据。

1 模型和方法

1.1 生存分析风险模型

生存分析（survival analysis）是一种根据实验或调查数据，将事件的结果（终点事件）和出现这一结果所经历的时间结合起来分析的一种统计分析方法，也称之为风险模型或持续模型（hazard model／duration model）［7］。目前生存分析已广泛应用于生物工程、社会科学等多个领域，近年来也逐步被运用到城市交通研究中，部分学者运用生存分析方法研究了交通事故的清理时间［8］、基于活动的出行行为［9］以及机非混行的通行时间［10］等问题。

广义的生存时间指生物体存活的时间，或所关心的某种现象的持续时间。城市购物出发时间指从凌晨开始，一直到出发去购物为止的持续时间［11］，属于广义生存时间范畴，可运用生存分析方法来对其进行研究。设T是非负的随机变量，表示的是从凌晨到出发去购物的持续时间。令f（t）表示T的概率密度函数，则T的分布函数为

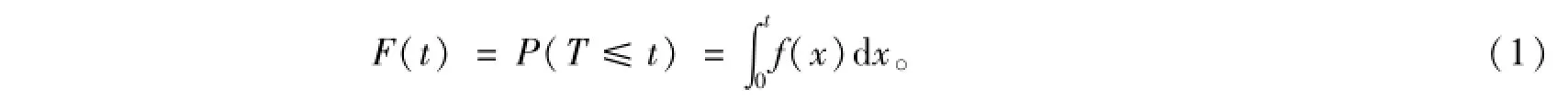
生存函数S（t），也叫累积生存率，表示生存时间大于t的概率。表达式为

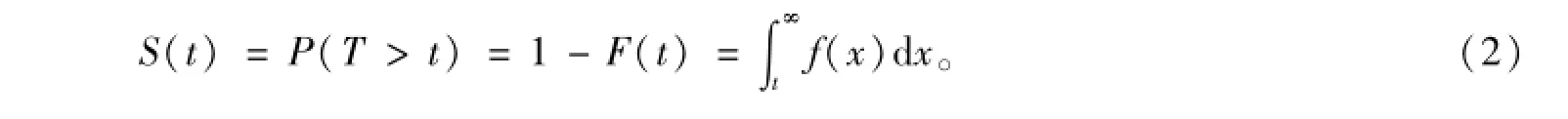
本研究中，由于没有删失观测值，生存函数可用在时刻t之前仍没有出去购物的人数占总样本的比例来估计，即

生存分析中，T的风险函数也叫危险率函数，指事件在持续到t时刻时没有结束，但在接下来的一段很小的时间Δt内结束的概率。用公式表示如下

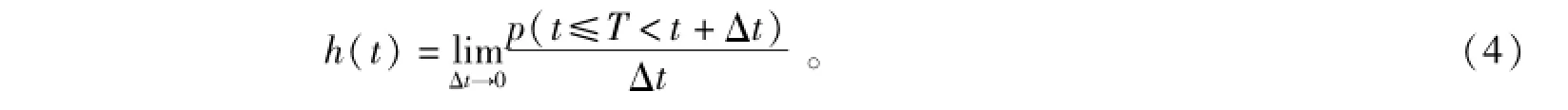
在本文中，风险函数指在时刻t之前没有出去购物，但在接下来的一段很小的时间Δt内出去购物的概率，可用下式来估计

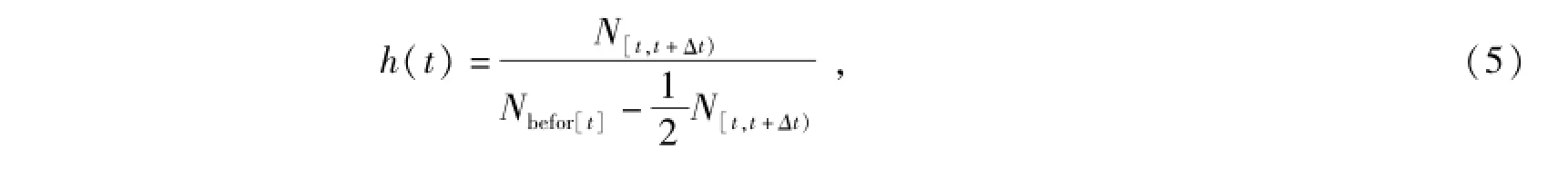
其中N［t，t＋Δt］表示在区间［t，t＋Δt］内出发购物的人数；Nbefor［t］表示在t时刻前未出发购物的人数。

风险函数与密度函数和生存函数之间有如下关系

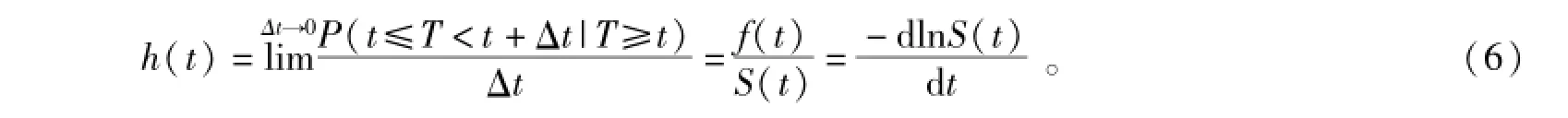
持续时间模型用风险函数和生存函数来描述事件的持续发展过程。从式（6）可知，风险函数是生存函数变化率的相反数，反映了事件持续过程的时间变化规律。

1.2 估计生存函数的非参数方法

生存分析通常采用生存函数、风险函数来描述，估计生存函数的方法有参数方法和非参数方法。当生存时间所服从的理论分布已知时用参数方法。当生存时间所服从的理论分布的类型未知时，非参数方法比参数方法有较高的效率，对数据的分布没有特殊的要求。参数模型的一个缺点是当参数形式不正确的时候，估计的风险函数也不正确。非参数模型的一个优点是不论资料是什么样的分布形式，只需要根据样本提供的顺序统计量对生存率进行估计。本研究中，我们采用非参数法，即Kaplan-Meier乘积限方法，来估计购物出发时间的生存函数。以城市购物出行行为为研究对象，假定共有n个出发时间样本，这些样本的出发时间共有k（k≤n）个不同的取值，由于没有删失数据，直接将它们从小到大排序t1＜t2＜…＜tk。令dj为tj－1到tj时段内出发去购物的样本数，nj为各时刻初未去购物的样本数。生存函数S（t）的乘积限估计可用下式表示

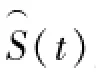
2 数据与实证分析

2.1 数据的提取和变量的定义

本研究以济南市2011年居民出行调查数据库为数据来源，调查的是一个工作日，一天中（0：00～20：00）的活动，调查包括家庭中所有成员的出行日志。出行日志包括出行的目的、出行的方式、出发的时刻、出发地、到达地、出行方式、所居住小区的性质等。另外，调查还包括个人和家庭的社会经济属性变量，如年龄、性别、月交通支出、月收入和职业类型等。

文章重点分析城市购物出行的出发时间，样本来自1 246个外出购物者。表1提供的是购物出发相关变量及其定义。

表1 变量的定义及取值Table 1 Definition and value of the variables

2.2 购物出发时间的总体分布

运用1中介绍的生存函数非参数估计方法，可求出购物出发时间的生存函数及其风险函数。样本的最早出发时间为2：00。表2给出了样本的出发时间生存函数和风险函数的估计值，图1则给出了生存函数和风险函数随着购物出发时间的变化规律。

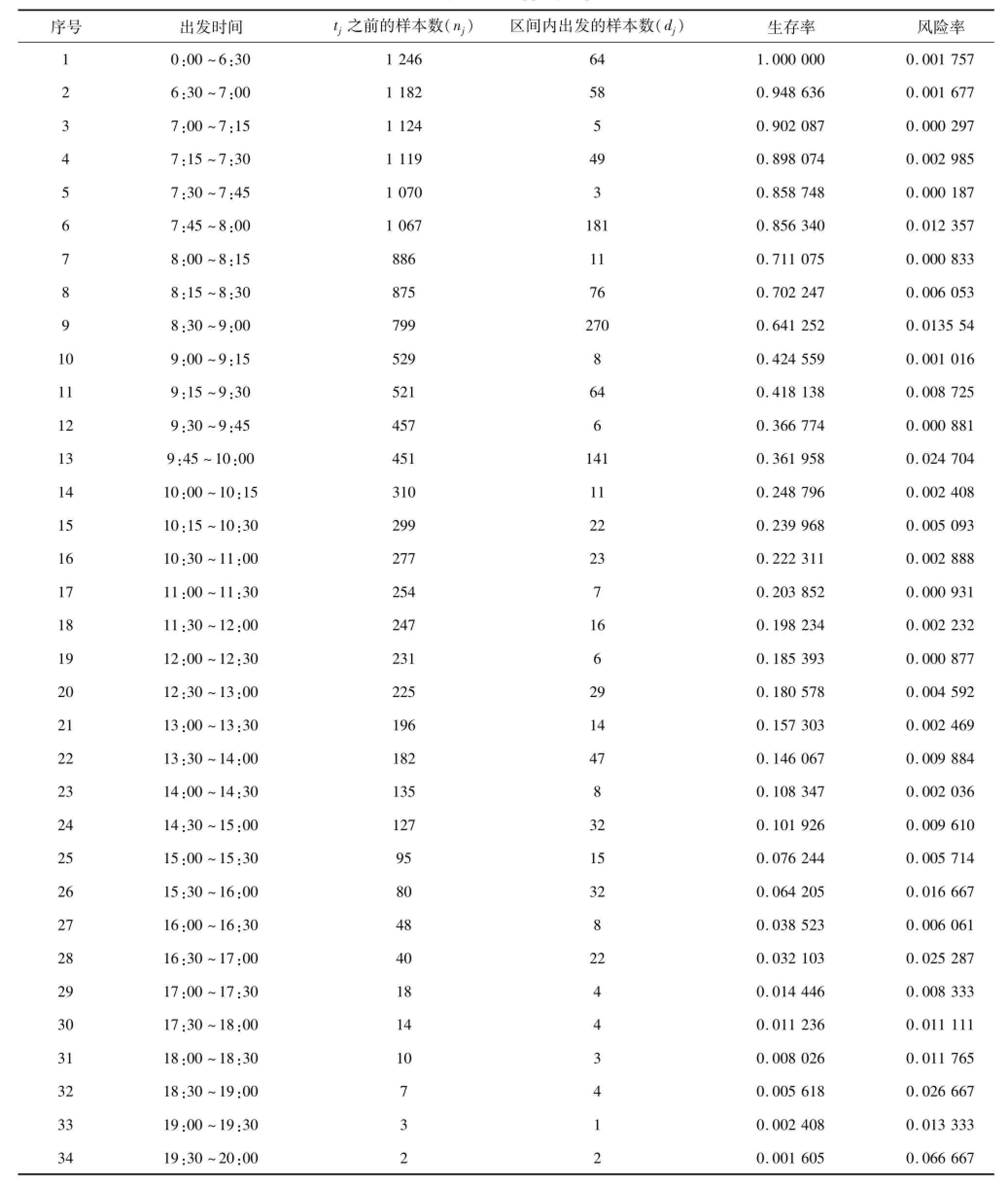
表2 购物出发时间的分析Table 2 Analysis of shopping departure time

由图1a生存函数曲线可知，在7：00之前，生存率变化较平稳，占到总体样本的5.4%，表明在此时段出去购物的人很少。在7：00～10：00之间生存率急剧下降，样本占到总体的69.7%，说明购物人群中有近70%的比例选择在这一时段内出发。在10：00之后变化较平稳，占到总体样本的24.9%。由图1b风险率函数可知，该函数不是单调的，在8：00～10：00之间出现购物高峰，加入购物的概率比较大。在10：00～16：00风险率较平稳，说明10：00没有出去购物的人在这一时段内出去购物的可能性不大。在16：00之后，随着时间的延长，风险率函数趋势是上升的，说明在16：00前仍未去购物的人群，在这之后出去购物的可能性越来越大。

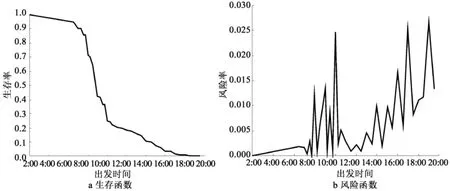
图1 购物出发时间的生存函数和风险率函数曲线Fig.1 Survival and dangerous functions curves of shopping departure time

表3给出了样本出行时间分布情况，T（min）表示0：00到出发去购物的持续时间。由表3可知，75%分位点为600 min（10：00），表明很大比例的购物人群是在10：00之前出去的。

表3 购物出发时间统计Table 3 Statistics of shopping departure time

2.3 变量的影响

除了购物出发时间的整体分布规律之外，各属性变量对购物出发时间分布也有一定影响。本文运用生存分析的KM方法来分析各变量对购物出发时间的影响，通过生存分析中的非参数方法对各变量在不同取值下的生存率和风险率函数进行比较，可以得出各变量对出发时间选择的影响。由于7：00～10：00的样本占到总体的将近70%，本文将重点针对这一时间段内购物人群的出发时间及其影响因素进行分析，见图2～4。

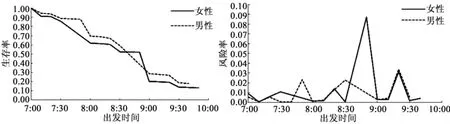
图2 性别对购物出发时间的生存函数和风险函数的影响Fig.2 Impact of gender on survival and dangerous functions of shopping departure time

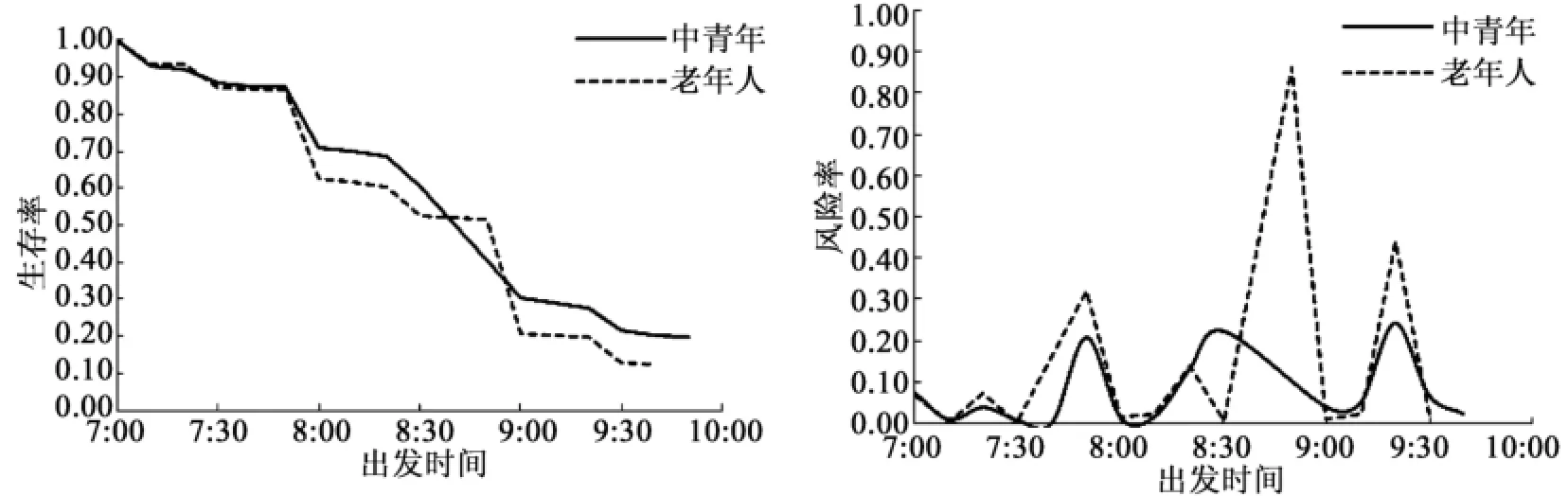
图3 年龄对购物出发时间的生存函数和风险函数的影响Fig.3 Impact of age on survival and dangerous functions of shopping departure time

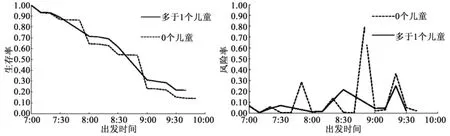
图4 家庭中儿童数量对购物出发时间的生存函数和风险函数的影响Fig.4 Impact of children amount on survival and dangerous functions of shopping departure time

由图2～4可以看出，性别、年龄和家中有无儿童对购物出发时间有显著影响。从不同性别的生存函数曲线（图2）可以看出，男性外出购物的生存函数一般比女性的低，这说明女性的购物出行活动总体比男性更多。另外，从风险函数曲线可以看出，男性外出购物的风险率变化较为平缓，说明男性在7：00～10：00之间购物出行的时间分布上比较均匀；而女性外出购物的风险函数的变化较为明显，在8：50前后有个明显的高峰值，对应的生存函数曲线上这一时段内生存率有急剧的下降趋势（由50%迅速下降到20%），表明样本中有近30%的女性选择在8：50前后出发去购物。

从不同年龄段的生存曲线（图3）可以看出，8：40之前，老年人外出购物的生存率曲线一般低于中青年，表明在这一时段内老年人出外购物的比例比中青年高，这可能与更多老年人有逛早市的习惯有关。此外，在7：40～8：50之间老年人外出购物的生存率曲线下降得很慢，表明在这一时段内老年人出外购物的比例非常低。从风险率曲线可以看出，中青年外出购物的曲线变化较为平缓，说明他们购物的出发时间分布更为均匀，而老年人外出购物的风险率函数中有几个明显的峰值，对应在生存率曲线上，老年人外出购物在7：40和8：50前后都有急剧的下降趋势，表明老年人的购物活动大多会选择在上班高峰期（7：40～8：50）之前或之后出行，以此避开上班高峰期。

家庭中儿童的数量也是影响购物出发时间的另一个重要因素。由图4可以看出，有儿童的家庭要比没有儿童的外出购物生存率要平稳，没有儿童的家庭外出购物在7：40和8：50出现生存率急剧下降，表明没有儿童的家庭在这两个时点前后出外购物的比例较高，以此避开上班高峰期，他们在购物出行时间选择上比有儿童的家庭更加灵活。家庭中有儿童的会在8：30左右出现第一个购物高峰，可能是由于这段时间内老人或家庭妇女带领儿童出来购物的比较多。

3 结论

本文通过非参数生存分析的方法分析了城市购物出发的时间分布，讨论了购物出发时间随出行者社会经济属性的连续分布规律，建立的出发时间的持续时间模型可以更好地分析购物出行的有效数据，为出行时间的定量研究提供了更准确有效的分析工具，对于准确把握居民购物出行行为有重要意义。利用模型得到的影响购物出发时间的显著因素主要是个人和家庭属性，而未考虑实时的道路状况［12］，今后应该对这方面做出更广泛的估计，包括更广泛的社会资源和争议性的变量。

［1］隽志才，鲜于建川.基于持续时间模型的日出行时间分析［J］.交通运输系统工程与信息，2010，10（4）：62－65.

［2］陈团生.通勤者出行行为特征与分析方法研究［D］.北京：北京交通大学，2007.

［3］ARENTZE，TA，TIMMERMANS，H JP.A Learning based transportation oriented simulation system.［J］.Transportation research part B：Methodological，2004，38（7）：613－633.

［4］ETTEMA D，BASTIN F，POLAK J，et al.Modelling the joint choice of activity timing and duration［J］.Transportation Research Part A，2007，41（9）：827－841.

［5］ETTEMA D，ASHIRU O，POLAK JW.Modeling tim ing and duration of activities and trips in response to road-pricing policies［J］.Transportation Research Record：Journal of the Transportation Research Board，2004，1894：1－10.

［6］LEE E T，WANG J.Statisticalmethods for survival data analysis［M］.New York：John Wiley＆Sons，Inc，2003.

［7］CHUNG Y.Development of an accident duration prediction model on the Korean Freeway Systems［J］.Accident Analysis and Prevention，2010，42（1）：282－289.

［8］van den BERG P，ARENTZE T，TIMMERMANSH.A latent class accelerated hazard model of social activity duration［J］. Transportation Research Part A：Policy and Practice，2012，46（1）：12－21

［9］GUO H W，GAO Z Y，YANG X B，et al.Modeling travel time underthe influence of on-street parking［J］.Journal of Transportation Engineering，2012，138（2）：229－235.

［10］YANG X B，HUAN M，GUO H W，et al.Car travel time estimation near a bus stop with non-motorized vehicles［J］. International Journal of Computational Intelligence Systems，2011，4（6）：1350－1357.

［11］BHATC R，STEED J L.A continuous-timemodel of departure time choice for urban shopping trips［J］.Transportation research part B：Methodological，2002，36（3）：207－224.

［12］GADDA S，KOCKELMAN KM，DAMIEN P，etal.Contimuous departure timemodels［J］.Transportation Research Record：Journal of the Transportation Research Board，2009，2132：13－24.

Nonparametric survival analysis of departure time of urban shopping trips

LI Ming，YANG Xiao-bao，HUAN Mei，DONG Ling
（School of Transportation and Traffic，Beijing Jiaotong University，Beijing 100044，China）

We addressed distribution characteristic of departure time of urban shopping trips based on the travel data of Jinan in 2011．We established its duration model with survival analysis method．We also estimated the duration time of shopping trips with a nonparametric method．We further discussed the impacts of departure time distribution of shopping trips and individual social-demographic properties on departure time of urban shopping trips．Results show that 5.4% of the total samples depart for shopping before 7：00，69.7% between 7：00 and 10：00，and less than 24.9% after 10：00．Gender，age and children amount of a family have significant impacts on departure time：females are early than males in departure time；elders are easier to go shopping at non-peak hours；departure time is more flexible for a no-child family．Our results can provide an accurate and effec tive analysis tool for quantitative investigation of departure time of shopping trips and have guiding significance for the controlof traffic congestion through dynamic pricing mechanism．

departure time of urban shopping trips；continuous time model；nonparametric survival analysis

U491

A

1002-4026（2014）04-0085-07

10.3976／j.issn.1002－4026.2014.04.015

2013-11-01

国家重点基础研究发展计划（973计划）（2012CB725400）；国家自然科学基金（70901005；71071016；71131001）

李明（1990－），女，硕士，研究方向为智能交通工程。Email：12120965＠bjtu.edu.cn