轴向激励作用下钻柱的瞬态动力学建模与分析

吴欣袁，张文华，冯 强，杨文领，游润仙

（中国石油集团渤海钻探工程有限公司工程技术研究院，天津300457）①

轴向激励作用下钻柱的瞬态动力学建模与分析

吴欣袁，张文华，冯 强，杨文领，游润仙

（中国石油集团渤海钻探工程有限公司工程技术研究院，天津300457）①

在复杂结构井钻井过程中，由于摩阻转矩、粘滑、托压等影响，导致难以达到预定的靶点。近年来研制了一些辅助振动工具，例如水力振荡器、扭转冲击器等。这些工具的使用起到了提升钻进效率、延长水平段长度的作用。建立了在轴向激励作用下钻柱的瞬态动力学模型，该模型包括1个一维动力学模型和1个三维静态模型。运用该模型可预测复杂三维井眼轨迹和激励作用下钻柱的力学行为。分析了振幅、频率、摩擦因数、传播距离等影响因素，推导出了加入振动激励后钻柱和井壁之间的表观摩擦因数，并计算了振荡类工具的合理安放位置。该模型和计算结果为水力振荡器的设计和现场应用提供了理论依据。

钻柱；水力振荡器；动力学；分析

随着国内外各大油田开发的深入，复杂结构井，例如：大位移井、超长水平井、多分支水平井等数量越来越多。一方面摩阻和转矩限制了水平段长度的延伸，另一方面钻柱中有害的振动又影响了钻柱的寿命。为了解决这些问题，许多学者在这方面做了深入的研究［1-3］，并研发出了一些工具来缓解这一矛盾［4-5］。近年来出现了一些振动工具，例如水力振荡器、扭转冲击器等。这些工具减小摩阻，缓和了有害振动，提高了钻进效率，延长了水平段长度，因此迅速得到推广应用。国内，一些钻探公司对轴向振荡工具引进吸收，现场应用多口井，取得了一些效果和实践经验［6-8］。然而，目前国内在这方面的研究主要集中在工具的结构研发和现场应用上，还没有从理论上建立模型来分析和预测振荡工具的效果。

本文旨在建立存在轴向激励作用下钻柱的瞬态动力学模型，并分析振幅、频率、摩擦因数等因素对激励的传播和减摩阻效果的影响。模型采用了有限差分网格法，将钻柱分为若干有限单元，并建立时间迭代方法，在描述管柱和井壁作用时引入了粘弹性集总参数模型，可描述振动作用下钻柱和井壁之间的碰撞。并且，本文使用一维动力学模型和三维静力学模型相互结合的方式，简化了计算过程。通过模拟计算，得出了激励在钻柱中的传播距离，推导出加入激励以后钻柱和井壁之间的表观摩擦因数，提出了振荡工具合理安放位置的建议，为水力振荡器这一类工具的设计和现场应用提供了理论依据。

1 模型的建立

钻柱瞬态动力学模型的建立过程包括5个步骤：

1） 在一定的假设条件下建立离散化模型。

2） 建立瞬态动力学模型的时间迭代方法。

3） 管柱和井壁之间边界条件的描述。

4） 建立运动方程。

5） 收敛判断。

1.1 建立离散化模型

本文建立的钻柱瞬态动力学模型所用的有限差分网格。如图1所示，将钻柱分为若干圆柱形刚体单元，每个单元具有1个几何中心，1个质量中心和2个连接中心。单元的长度应小于管柱直径的2～3倍，这样才能更好地表现为刚体属性。假设当钻柱为直线状态时，其质量中心和几何中心重叠。钻柱发生弯曲时，如果质心不在几何中心，假设质心在垂直于其主轴方向离几何中心一定距离d1处。

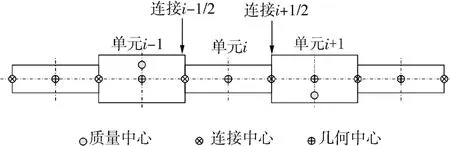
图1 有限差分网格

1.2 建立时间迭代方法

图2为时间迭代图。其中：v为单元的轴向线速度，ω为单元的角速度，r为沿井眼轴线移动的距离（d1、d2、d3分别表示3个方向）；f、M分别是使单元结合在一起的内部力和力矩。

管柱单元的线速度和角速度在时刻（t0＋nΔt）更新其值，其中n为正整数。位移和方向在时刻（t0＋（n＋1／2）Δt）更新其值，假设之前计算的速度值为［（t0＋（n-1／2）Δt），（t0＋（n＋1／2）Δt）］时间间隔内的平均值。当位移和方向值更新以后，在时刻（t0＋（n＋1／2）Δt），连接点处的内部力和力矩就可以计算出来。本文中假设钻柱为线弹性材料，因此，内部力和力矩就是2个相邻单元的相对位移和方向的变化量的函数。在（t0＋（n＋1）Δt）时刻，更新线速度和角速度，假设前一步计算的内部力和力矩为时间间隔［（t0＋nΔt），（t0＋（n＋1）Δt）］的平均值。

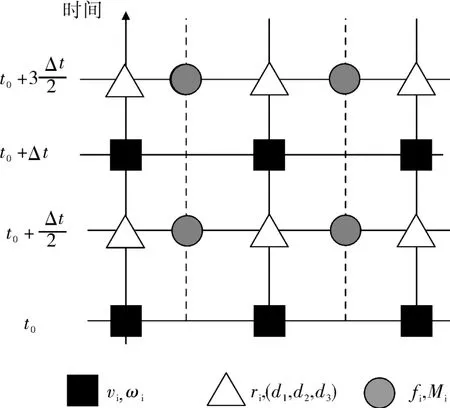
图2 时间迭代图

1.3 边界条件的描述

本文采用了粘弹性边界集总参数模型［7-9］来描述钻柱和井壁之间的作用，能很好地获得在加入激励以后钻柱与井壁相互碰撞运动速度和加速度。如图3所示，为粘弹性边界集总参数模型。其中，3个参数K、B、μ描述了钻柱与井壁之间的相互作用。K为管柱-井壁两相系统的组合刚度系数。垂直于井壁的力，其大小是管柱和井壁之间的瞬时干涉深度的函数。干涉深度是如果岩石和管柱都为刚性体时，管柱渗透入井壁的深度。这个力的大小计算使用圆柱体干涉的赫兹接触方程。该方法的组合刚度等效表示，可用两组串联的弹簧，一组是线弹性弹簧来表示管柱横截面，另一组非线性弹簧来表示圆柱体接触影响。B为管柱-井壁相互作用的恢复系数。该系数是两个刚体之间有碰撞时反弹速度和接近速度之间的比值。这2个速度都是沿接触表面的法线方向测量的速度。这个参数有效地表示了边界的粘性性质。恢复系数可以根据一系列的岩石类型进行实验测量。μ为管柱-井壁之间的摩擦因数，用于计算管柱和井壁点接触的摩擦力。

图3 粘弹性边界集总参数模型

1.4 建立运动方程

根据上述模型描述，将一个典型的管柱单元考虑为刚体时，它的运动方程如下：

其中i，j＝1，2，3，Fi为净力，Ti为转矩（作用在单元上，沿其主轴方向，包括了泥浆引起的）。因此它们就分别表示了线速度和角速度的函数。

1.5 收敛判断

这个系统是6个耦合非线性微分方程，并使用牛顿-拉夫逊迭代来求解。对该方程使用中央差分，可以写成一般形式：

式中：x是线性速度和角速度的矢量；M是惯性矩阵；f是力函数的矢量。

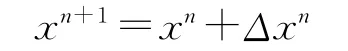
在第1次迭代中，

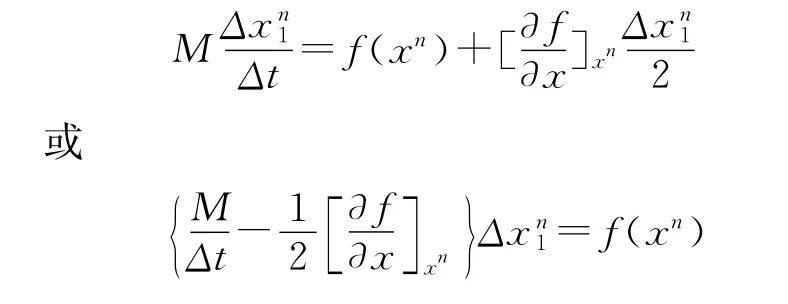
这可以用来计算第1次预计速度的增量Δx1。当有了第1次速度增量，就可以使用修改的方程来精简求解过程：

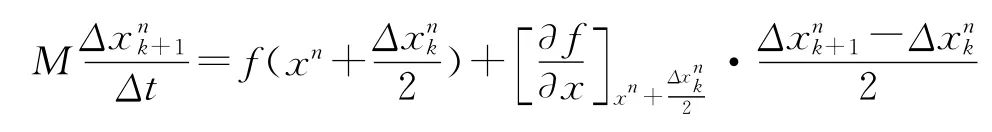
式中：Kext表示两个相邻单元的拉伸刚度；Ktor表示两个相邻单元的等效扭转刚度；L表示单元的长度；A表示单元的横截面积；G表示单元材料的剪切模量；E表示单元材料的杨氏模量。

通过计算表明，达到3次迭代后收敛。

2 计算结果分析

本文以连续油管柱存在轴向激励为例进行力学行为分析。该连续油管柱的水平段长度为1 828.8 m，外径50.8 m m，壁厚4 m m。在管柱的最右端施加1个随时间变化的正弦轴向激励，输出力的振幅为8 896.4 N。在管柱的最左端施加1个无载荷边界条件。

2.1 激励在管柱中的传播

激励在管柱中的传播如图4所示，可以看到轴向激励从右端沿管柱向其左边传递。载荷的大小在传递过程中由于摩擦损耗，而逐渐减小，达到一定距离后降为零。

图4 激励在管柱中的传播距离与轴向载荷关系曲线

2.2 频率对激励传播的影响

为了分析频率对激励传播的影响，计算了多种频率下同样大小的激励传播的情况。如图5为10 H z和100 H z时激励在钻柱中的传播。从图5中可以看到，两者图形非常相似，得出传播距离也基本相等。因此，可以得出激励在管柱中的传播与频率相关性较小。

图5 频率为10 H z和100 H z的激励在管柱中的传递

2.3 摩擦因数对激励传播的影响

不同摩擦因数情况下激励在管柱中的传递如图6所示。从二者的比较可以看出，摩擦因数越大，轴向激励沿管柱传播的距离越短，更难以传递到管柱的另一端。

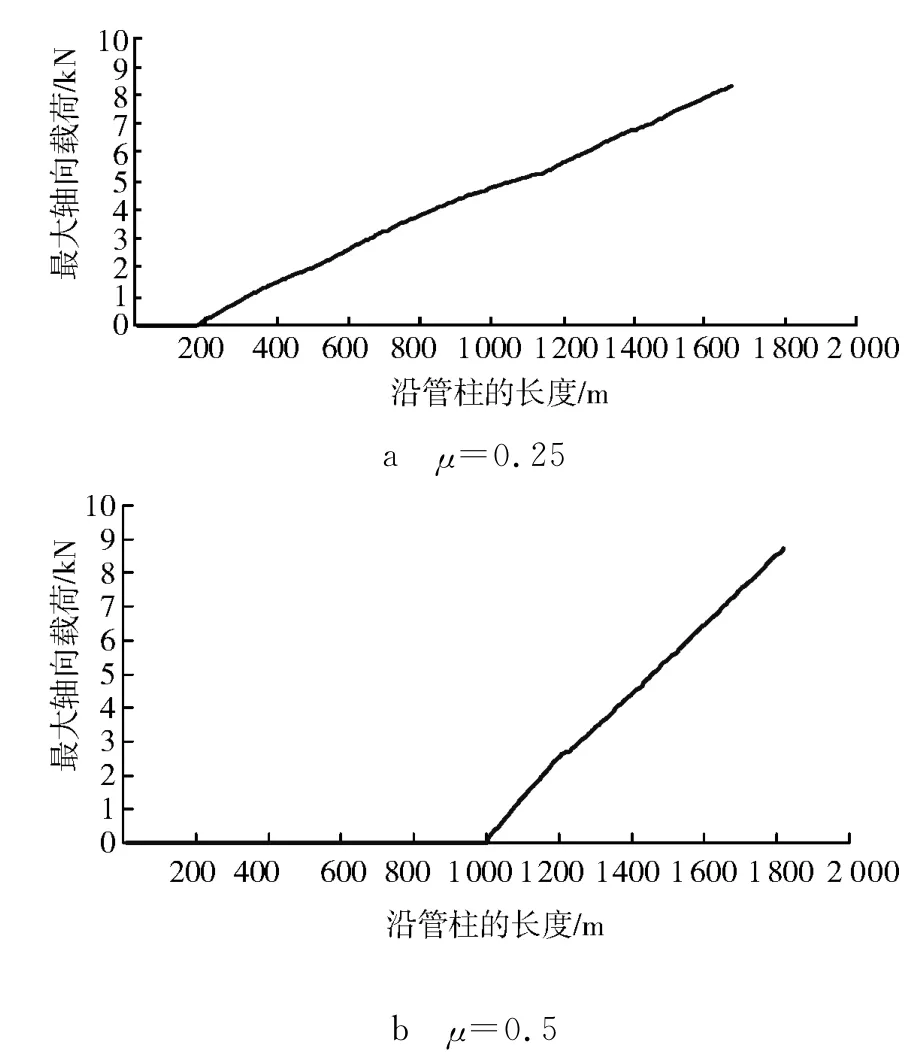
图6 摩擦因数为0.25和0.5时激励在管柱中的传递

2.4 激励的传播距离

通过计算分析，在较宽的范围内（10～200 H z），可以推导出激励传播距离的公式：

式中：Lp是传播距离；Fa是轴向激励的载荷振幅；μ是动摩擦因数；ρAg是单位长度管柱在钻井液中的重力。

2.5 激励对摩阻的作用

如图7所示，在0 s时在管柱的左端施加1个10.2 k N的推力，显然这个力是不够推动管柱克服摩擦力而移动的（小于20.7 k N），在1.25 s后在管柱的右端施加1个正弦轴向激励，通过计算分析管柱的力学行为。从图7中可以看到，1个较小的力在激励作用下将管柱推动向右移动。因此，这个系统中表现出来的摩擦因数降低了。在此可以定义一个表观摩擦因数来表示存在轴向激励时管柱和井壁之间的摩擦因数μ′。应用激励之前推动管柱所需力为F，应用激励之后推动管柱所需力为F′。

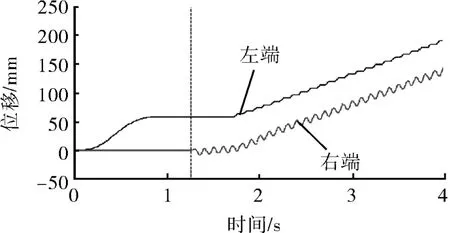
图7 激励作用下管柱的力学行为

3 模型的应用

1） 计算水力振荡器的排量、压降、输出载荷等，作为设计依据。

2） 确定工具在钻柱中的合理安放位置。应该满足2个基本条件：①距钻头的距离应尽量不大于激励在管柱中的传播距离的1／2，否则工具起到的降摩阻作用会降低，该距离可以用文中推导的公式计算出来，若是斜井可通过最小侧向力进行计算；②工具位置距M W D、L W D等井下仪器的距离不应太近，否则容易影响仪器的工作。

3） 工具的应用效果预测。使用该模型，在工具下井之前，就能预测出工具的减摩阻效果。例如苏76-1-20 H井（这是渤海钻探所钻超长水平段水平井），在该井4次使用了水力振荡工具，如表1所示。在前2次使用过程中，因为安放位置过于靠近仪器，导致仪器无信号；第3次，由于该井段伽马值突然升高，岩性变致密，因此在滑动钻进过程中，钻速提高并不明显；第4次，效果显著，滑动钻速提高了79.21%。

表1 苏76-1-20 H井水力振荡工具使用情况

如果使用了本文所建模型计算分析，在下井前就能确定工具最佳安放位置，并预测大致应用效果，避免出现复杂情况。图8为模型预测的不同钻具和不同安放位置下钻柱中的最大摩阻。

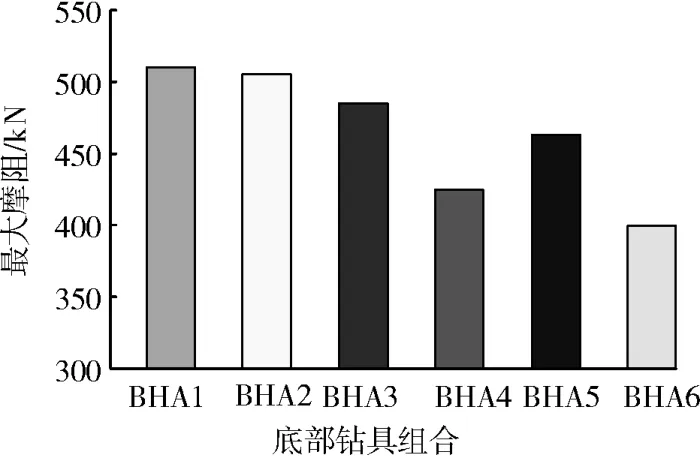
图8 不同底部钻具组合钻柱的最大摩阻

4 结论

1） 建立了轴向激励作用下钻柱的瞬态动力学模型。采用了一维动力学模型和三维静力学模型的组合方法，使得计算更加简便、快捷。其计算结果可以作为水力振荡器的设计依据，并指导现场应用。

2） 分析了载荷、频率、摩擦因数对摩阻力的影响，认为激励的载荷大小决定了振荡工具的效果，而初步认为其频率与减小摩阻相关性不大。

3） 推导出了存在轴向激励情况下，管柱和井壁之间的表观摩擦因数。认为推动整个管柱所需的最小力（钻压），相当于管柱的长度减去激励传播的长度，得出的剩余管柱长度所引起的摩擦力大小。

4） 根据模型分析，提出振荡类工具的合理安放位置。距钻头的距离应尽量不大于激励在管柱中的传播距离的1／2，否则工具起到的降摩阻作用会降低。该距离可以用文中推导的公式计算出来，若是斜井可通过最小侧向力进行计算；工具位置距M W D、L W D等井下仪器的距离不应太近，否则容易影响仪器的工作。

5） 频率的大小虽然对降摩阻效果影响不大，但是对其他井下仪器的影响非常大，是振荡工具的一个重要参数。下一步应研究分析振荡工具和井下仪器的频率叠加问题，提高这类工具的现场适应性。

［1］ Craig A D，Goodship R，Shearer D R.High Frequency Dow nholeDynamicM easurementsProvideGreater U nderstanding of DrillingVibration inPerfro mance M otor Asse m blies［C］／／SP E Paper 128211，presented at SP E／IA D C Drilling Conference，New Orleans.2010.

［2］ Bailey J R，Biediger E A O，Ertas D，et al.Drilling Vibrations M odeling and Field Validation［C］／／SP E 112 650，resented at the SP E／IA D C Drilling Conference，Florida.2008.

［3］ 王谊，施连海.水力脉动冲击钻井工具初步研究与试验［J］.石油钻探技术，2006，31（2）：51-52.

［4］ 王敏生，王智锋，李作会.水力脉冲式钻井工具的研制与应用［J］.石油机械，2006，34（5）：27：-29.

［5］ 曹丽平，雷民生，鲍远敦，等.油井液动冲击器的应用［J］.石油矿场机械，2005，34（4）：100-101.

［6］ 倪红坚，韩来聚，马清明.水力脉冲诱发井下工具研究［J］.石油钻采工艺，2006，28（2）：15-19.

［7］ 李昱，张海滨.液动冲击旋转钻井技术及其发展趋势［J］.石油矿场机械，2006，35（3）：107-109.

［8］ Clayton R，Detournay E，Fear M，et al.Influence of bitrock interaction on stick-slip vibrations of P D C bits［C］／／SP E 77616，presented at SP E／IA D C Drilling Conference，Texas.2002.

［9］ 石崇东，党克军，张军.水力振荡器在苏36-8-18 H井的应用［J］.石油机械，2012，40（3）：35-39.

［10］ 丁培积，陈天成，刘嘉铭，等．水平井水力加压工具及其应用［J］.石油钻探技术，1995，23（3）：41-43.

［11］ 高建强，陈朝达.液动冲击钻具存在问题及解决途径［J］.西安石油学院学报（自然科学版）1998，13（3）：62-68.

［12］ Robertson L，M ason C J，Sherwood A S，et al.Dynamic Excitation Tool：Developmental Testing and C T D Field Case Histories［C］／／SPE 89519，presented at the SPE／ICoTA Coi led Tubing and W ell Intervention Conference and Exhibition held in H ouston，Texas.2004.

［13］ Schen A E，Snell A D，Stanes B H.O ptimization of Bit Drilling Performance Using a New S mall Vibration Logging Tool［C］／／SP E／IA D C 92336，presented at the SP E／IA D C Drilling Conference held in A msterdam，The Netherlands.2005.

［14］ Tongs T，Hinrichs A，Spickett R，et al.Ultra deep Extended-Reach Si m ulations［C］／／SP E106874，presented at the SP E／ICoT A Coiled Tubing and W ell Intervention Conference and Exhibition held in The W oodlands，Texas.2007.

M odeling and Analysis of Drill Stem Transient Dynamic under Axial Excitation

W U Xin-yuan，Z H A N GW en-hua，F E N G Qiang，Y A N GW en-ling，Y O U Run-xian
（Engineering Technology Research Institute，B H D C，Tianjin300457，China）

In the process of drilling co m plex structure wells，because the friction＆torque，stickslip，prop pressure and other effects，making it difficult to achieve the desired targets.In recent years，a nu m ber of auxiliary vibrating tools were developed，such as hydraulic oscillators，reversing shock，etc.Using these tools can im prove drilling efficiency，prolonging the length of the horizontal section.A role in the axial excitation transient dyna mics m odel drillstring was established.T he m odel consists of a one-dimensional dyna mic m odel and a three-dimensional static m odel.T he m odelis applied to co m plex three-dimensional trajectory prediction and incentives under the mechanical behavior of the drill string.T he a m plitude，frequency，friction coefficient，transmission distance and other factors were analyzed，and deduced after adding vibration excitation between the drill string and the borehole wall apparent friction coefficient.A nd reasonable oscillation tools placement reco m mendations are put forward.T he m odel and calculation results provide a theoretical basis for the hydraulic oscillator of this type of tool design and field applications.

drill stem；hydraulic oscillator；dyna mics；analysis

T E921.201

A

10.3969／j.issn.1001-3482.2014.08.002

1001-3482（2014）08-0008-05

2014-02-26

吴欣袁（1981-），男，四川宜宾人，工程师，博士，2012年毕业于西南石油大学油气井工程专业，主要从事井下工具研发、油气井工程力学等研究，E-mail：sw pu w xy＠126.co m。